Merge pull request #77 from 4ndrelim/branch-RefactorAVL

docs: Improve clarity for Radix and complete AVL docs

Author: 4ndrelim

docs/assets/images/AvlTree.png

@@ -1,68 +1,81 @@
 # Radix Sort
 
 ## Background
-
 Radix Sort is a non-comparison based, stable sorting algorithm that conventionally uses counting sort as a subroutine.
 
 Radix Sort performs counting sort several times on the numbers. It sorts starting with the least-significant segment 
-to the most-significant segment.
+to the most-significant segment. What a 'segment' refers to is explained below. 
 
-### Segments
-The definition of a 'segment' is user defined and defers from implementation to implementation.
-It is most commonly defined as a bit chunk.
+### Idea
+The definition of a 'segment' is user-defined and could vary depending on implementation.
 
-For example, if we aim to sort integers, we can sort each element
-from the least to most significant digit, with the digits being our 'segments'.
+Let's consider sorting an array of integers. We interpret the integers in base-10 as shown below.  
+Here, we treat each digit as a 'segment' and sort (counting sort as a sub-routine here) the elements 
+from the least significant digit (right) to most significant digit (left). In other words, the sub-routine sort is just
+focusing on 1 digit at a time.
 
-Within our implementation, we take the binary representation of the elements and
-partition it into 8-bit segments. An integer is represented in 32 bits,
-this gives us 4 total segments to sort through.
+<div align="center">
+    <img src="../../../../../../docs/assets/images/RadixSort.png" width="65%">
+    <br>
+    Credits: Level Up Coding
+</div>
 
-Note that the number of segments is flexible and can range up to the number of digits in the binary representation.
-(In this case, sub-routine sort is done on every digit from right to left)
+The astute would note that a **stable version of counting sort** has to be used here, otherwise the relative ordering
+based on previous segments might get disrupted when sorting with subsequent segments.
 
-![Radix Sort](https://miro.medium.com/v2/resize:fit:661/1*xFnpQ4UNK0TvyxiL8r1svg.png)
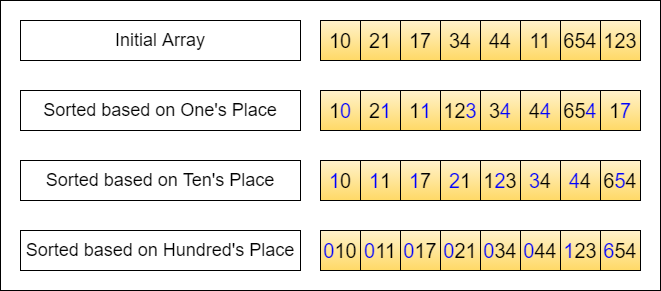+### Segment Size
+Naturally, the choice of using just 1 digit in base-10 for segmenting is an arbitrary one. The concept of Radix Sort 
+remains the same regardless of the segment size, allowing for flexibility in its implementation.
 
-We place each element into a queue based on the number of possible segments that could be generated.
-Suppose the values of our segments are in base-10, (limited to a value within range *[0, 9]*),
-we get 10 queues. We can also see that radix sort is stable since
-they are enqueued in a manner where the first observed element remains at the head of the queue
+In practice, numbers are often interpreted in their binary representation, with the 'segment' commonly defined as a 
+bit chunk of a specified size (usually 8 bits/1 byte, though this number could vary for optimization).
 
-*Source: Level Up Coding*
+For our implementation, we utilize the binary representation of elements, partitioning them into 8-bit segments. 
+Given that an integer is typically represented in 32 bits, this results in four segments per integer. 
+By applying the sorting subroutine to each segment across all integers, we can efficiently sort the array. 
+This method requires sorting the array four times in total, once for each 8-bit segment,
 
 ### Implementation Invariant
+At the end of the *ith* iteration, the elements are sorted based on their numeric value up till the *ith* segment.
 
-At the start of the *i-th* segment we are sorting on, the array has already been sorted on the
-previous *(i - 1)-th* segments.
-
-### Common Misconceptions
-
-While Radix Sort is non-comparison based,
-the that total ordering of elements is still required.
-This total ordering is needed because once we assigned a element to a order based on a segment,
-the order *cannot* change unless deemed by a segment with a higher significance.
-Hence, a stable sort is required to maintain the order as
-the sorting is done with respect to each of the segments.
+### Common Misconception
+While Radix Sort is a non-comparison-based algorithm, 
+it still necessitates a form of total ordering among the elements to be effective. 
+Although it does not involve direct comparisons between elements, Radix Sort achieves ordering by processing elements 
+based on individual segments or digits. This process depends on Counting Sort, which organizes elements into a 
+frequency map according to a **predefined, ascending order** of those segments.
 
 ## Complexity Analysis
-Let b-bit words be broken into r-bit pieces. Let n be the number of elements to sort.
+Let b-bit words be broken into r-bit pieces. Let n be the number of elements.
 
 *b/r* represents the number of segments and hence the number of counting sort passes. Note that each pass
-of counting sort takes *(2^r + n)* (O(k+n) where k is the range which is 2^r here).
+of counting sort takes *(2^r + n)* (or more commonly, O(k+n) where k is the range which is 2^r here).
 
 **Time**: *O((b/r) * (2^r + n))*
 
-**Space**: *O(n + 2^r)*
+**Space**: *O(2^r + n)* <br>
+Note that our implementation has some slight space optimization - creating another array at the start so that we can
+repeatedly recycle the use of original and the copy (saves space!), 
+to write and update the results after each iteration of the sub-routine function.
 
 ### Choosing r
-Previously we said the number of segments is flexible. Indeed, it is but for more optimised performance, r needs to be
+Previously we said the number of segments is flexible. Indeed, it is, but for more optimised performance, r needs to be
 carefully chosen. The optimal choice of r is slightly smaller than logn which can be justified with differentiation.
 
-Briefly, r=lgn --> Time complexity can be simplified to (b/lgn)(2n). <br>
-For numbers in the range of 0 - n^m, b = mlgn and so the expression can be further simplified to *O(mn)*.
+Briefly, r=logn --> Time complexity can be simplified to (b/lgn)(2n). <br>
+For numbers in the range of 0 - n^m, b = number of bits = log(n^m) = mlogn <br>
+and so the expression can be further simplified to *O(mn)*.
 
 ## Notes
-- Radix sort's time complexity is dependent on the maximum number of digits in each element,
-  hence it is ideal to use it on integers with a large range and with little digits.
-- This could mean that Radix Sort might end up performing worst on small sets of data
-  if any one given element has a in-proportionate amount of digits.
+- Radix Sort doesn't compare elements against each other, which can make it faster than comparative sorting algorithms 
+like QuickSort or MergeSort for large datasets with a small range of key values
+  - Useful for large sets of numeric data, especially if stability is important
+  - Also works well for data that can be divided into segments of equal size, with the ordering between elements known
+  
+- Radix sort's efficiency is closely tied to the number of digits in the largest element. So, its performance 
+might not be optimal on small datasets that include elements with a significantly higher number of digits compared to 
+others. This scenario could introduce more sorting passes than desired, diminishing the algorithm's overall efficiency.
+  - Avoid for datasets with sparse data
+
+- Our implementation uses bit masking. If you are unsure, do check 
+[this](https://cheever.domains.swarthmore.edu/Ref/BinaryMath/NumSys.html ) out

docs/assets/images/BalancedProof.png

@@ -16,9 +16,9 @@ public class RadixSort {
      * @return The value of the digit in the number at the given segment.
      */
     private static int getSegmentMasked(int num, int segment) {
-        // Bit masking here to extract each segment from the integer.
-        int mask = ((1 << NUM_BITS) - 1) << (segment * NUM_BITS);
-        return (num & mask) >> (segment * NUM_BITS);
+        // bit masking here to extract each segment from the integer.
+        int mask = (1 << NUM_BITS) - 1;
+        return (num >> (segment * NUM_BITS)) & mask;  // we do a right-shift on num to focus on the desired segment
     }
 
     /**
@@ -28,7 +28,7 @@ private static int getSegmentMasked(int num, int segment) {
      * @param sorted output array.
      */
     private static void radixSort(int[] arr, int[] sorted) {
-        // sort the N numbers by segments, starting from left-most segment
+        // Code in the loop is essentially counting sort; sort the N numbers by segments, starting from right-most
         for (int i = 0; i < NUM_SEGMENTS; i++) {
             int[] freqMap = new int[1 << NUM_BITS]; // at most this number of elements
 

docs/assets/images/RadixSort.png

@@ -55,7 +55,7 @@ public int height(T key) {
     }
 
     /**
-     * Update height of node in avl tree during rebalancing.
+     * Update height of node in avl tree for re-balancing.
      *
      * @param n node whose height is to be updated
      */
@@ -372,6 +372,10 @@ private T successor(Node<T> node) {
         return null;
     }
 
+
+    // ---------------------------------------------- NOTE ------------------------------------------------------------
+    // METHODS BELOW ARE NOT NECESSARY; JUST FOR VISUALISATION PURPOSES
+
     /**
      * prints in order traversal of the entire tree.
      */
@@ -390,13 +394,9 @@ private void printInorder(Node<T> node) {
         if (node == null) {
             return;
         }
-        if (node.getLeft() != null) {
-            printInorder(node.getLeft());
-        }
+        printInorder(node.getLeft());
         System.out.print(node + " ");
-        if (node.getRight() != null) {
-            printInorder(node.getRight());
-        }
+        printInorder(node.getRight());
     }
 
     /**
@@ -408,7 +408,6 @@ public void printPreorder() {
         System.out.println();
     }
 
-
     /**
      * Prints out pre-order traversal of tree rooted at node
      *
@@ -419,12 +418,8 @@ private void printPreorder(Node<T> node) {
             return;
         }
         System.out.print(node + " ");
-        if (node.getLeft() != null) {
-            printPreorder(node.getLeft());
-        }
-        if (node.getRight() != null) {
-            printPreorder(node.getRight());
-        }
+        printPreorder(node.getLeft());
+        printPreorder(node.getRight());
     }
 
     /**
@@ -442,12 +437,11 @@ public void printPostorder() {
      * @param node node which the tree is rooted at
      */
     private void printPostorder(Node<T> node) {
-        if (node.getLeft() != null) {
-            printPostorder(node.getLeft());
-        }
-        if (node.getRight() != null) {
-            printPostorder(node.getRight());
+        if (node == null) {
+            return;
         }
+        printPostorder(node.getLeft());
+        printPostorder(node.getRight());
         System.out.print(node + " ");
     }
 

docs/assets/images/TreeRotation.png

@@ -15,10 +15,9 @@ public class Node<T extends Comparable<T>> {
     private Node<T> parent;
     private int height;
     /*
-     * Can insert more properties here.
-     * If key is not unique, introduce a value property
-     * so when nodes are being compared, a distinction
-     * can be made
+     * Can insert more properties here for augmentation
+     * e.g. If key is not unique, introduce a value property as a tie-breaker
+     * or weight property for order statistics
      */
 
     public Node(T key) {

src/main/java/algorithms/sorting/radixSort/README.md

@@ -0,0 +1,91 @@
+# AVL Trees
+
+## Background
+Is the fastest way to search for data to store them in an array, sort them and perform binary search? No. This will
+incur minimally O(nlogn) sorting cost, and O(n) cost per insertion to maintain sorted order.
+
+We have seen binary search trees (BSTs), which always maintains data in sorted order. This allows us to avoid the
+overhead of sorting before we search. However, we also learnt that unbalanced BSTs can be incredibly inefficient for
+insertion, deletion and search operations, which are O(h) in time complexity (in the case of degenerate trees,
+operations can go up to O(n)).
+
+Here we discuss a type of self-balancing BST, known as the AVL tree, that avoids the worst case O(n) performance 
+across the operations by ensuring careful updating of the tree's structure whenever there is a change 
+(e.g. insert or delete).
+
+### Definition of Balanced Trees
+Balanced trees are a special subset of trees with **height in the order of log(n)**, where n is the number of nodes. 
+This choice is not an arbitrary one. It can be mathematically shown that a binary tree of n nodes has height of at least
+log(n) (in the case of a complete binary tree). So, it makes intuitive sense to give trees whose heights are roughly
+ in the order of log(n) the desirable 'balanced' label.
+
+<div align="center">
+    <img src="../../../../../docs/assets/images/BalancedProof.png" width="40%">
+    <br>
+    Credits: CS2040s Lecture 9
+</div>
+
+### Height-Balanced Property of AVL Trees
+There are several ways to achieve a balanced tree. Red-black tree, B-Trees, Scapegoat and AVL trees ensure balance 
+differently. Each of them relies on some underlying 'good' property to maintain balance - a careful segmenting of nodes 
+in the case of RB-trees and enforcing a depth constraint for B-Trees. Go check them out in the other folders! <br>
+What is important is that this **'good' property holds even after every change** (insert/update/delete).
+
+The 'good' property in AVL Trees is the **height-balanced** property. Height-balanced on a node is defined as  
+**difference in height between the left and right child node being not more than 1**. <br>
+We say the tree is height-balanced if every node in the tree is height-balanced. Be careful not to conflate 
+the concept of "balanced tree" and "height-balanced" property. They are not the same; the latter is used to achieve the
+former.
+
+<details>
+<summary> <b>Ponder..</b> </summary>
+Consider any two nodes (need not have the same immediate parent node) in the tree. Is the difference in height 
+between the two nodes <= 1 too?
+</details>
+
+It can be mathematically shown that a **height-balanced tree with n nodes, has at most height <= 2log(n)** (
+in fact, using the golden ratio, we can achieve a tighter bound of ~1.44log(n)).
+Therefore, following the definition of a balanced tree, AVL trees are balanced.
+
+<div align="center">
+    <img src="../../../../../docs/assets/images/AvlTree.png" width="40%">
+    <br>
+    Credits: CS2040s Lecture 9
+</div>
+
+## Complexity Analysis
+**Search, Insertion, Deletion, Predecessor & Successor queries Time**: O(height) = O(logn)
+
+**Space**: O(n) <br>
+where n is the number of elements (whatever the structure, it must store at least n nodes)
+
+## Operations
+Minimally, an implementation of AVL tree must support the standard **insert**, **delete**, and **search** operations. 
+**Update** can be simulated by searching for the old key, deleting it, and then inserting a node with the new key. 
+
+Naturally, with insertions and deletions, the structure of the tree will change, and it may not satisfy the 
+"height-balance" property of the AVL tree. Without this property, we may lose our O(log(n)) run-time guarantee. 
+Hence, we need some re-balancing operations. To do so, tree rotation operations are introduced. Below is one example.
+
+<div align="center">
+    <img src="../../../../../docs/assets/images/TreeRotation.png" width="40%">
+    <br>
+    Credits: CS2040s Lecture 10
+</div>
+
+Prof Seth explains it best! Go re-visit his slides (Lecture 10) for the operations :P <br>
+Here is a [link](https://www.youtube.com/watch?v=dS02_IuZPes&list=PLgpwqdiEMkHA0pU_uspC6N88RwMpt9rC8&index=9) 
+for prof's lecture on trees. <br>
+_We may add a summary in the near future._
+
+## Application
+While AVL trees offer excellent lookup, insertion, and deletion times due to their strict balancing, 
+the overhead of maintaining this balance can make them less preferred for applications 
+where insertions and deletions are significantly more frequent than lookups. As a result, AVL trees often find itself
+over-shadowed in practical use by other counterparts like RB-trees, 
+which boast a relatively simple implementation and lower overhead, or B-trees which are ideal for optimizing disk 
+accesses in databases.
+
+That said, AVL tree is conceptually simple and often used as the base template for further augmentation to tackle 
+niche problems. Orthogonal Range Searching and Interval Trees can be implemented with some minor augmentation to 
+an existing AVL tree.

src/main/java/algorithms/sorting/radixSort/RadixSort.java

@@ -31,14 +31,21 @@ public void test_radixSort_shouldReturnSortedArray() {
         int[] fourthResult = Arrays.copyOf(fourthArray, fourthArray.length);
         RadixSort.radixSort(fourthResult);
 
+        int[] fifthArray =
+                new int[] {157394, 93495939, 495839239, 485384, 38439958, 3948585, 39585939, 6000999, 111111111, 98162};
+        int[] fifthResult = Arrays.copyOf(fifthArray, fifthArray.length);
+        RadixSort.radixSort(fifthResult);
+
         Arrays.sort(firstArray);
         Arrays.sort(secondArray);
         Arrays.sort(thirdArray);
         Arrays.sort(fourthArray);
+        Arrays.sort(fifthArray);
 
         assertArrayEquals(firstResult, firstArray);
         assertArrayEquals(secondResult, secondArray);
         assertArrayEquals(thirdResult, thirdArray);
         assertArrayEquals(fourthResult, fourthArray);
+        assertArrayEquals(fifthResult, fifthArray);
     }
 }