|
| 1 | +--- |
| 2 | +tags: ['计算机科学','GAN','对抗学习','NF','VAE','变分自编码器','投稿作品'] |
| 3 | +title: 变分推断与生成模型 |
| 4 | +date: '2022-08-13 18:06:01' |
| 5 | +categories: '计算机科学' |
| 6 | +cover: https://tva3.sinaimg.cn/large/006UcwnJly1h55efqdgjmj30rm0ckq5p.jpg |
| 7 | +copyright_author: '我本张逸仙' |
| 8 | +katex: true |
| 9 | +--- |
| 10 | + |
| 11 | +# 变分推断与生成模型 |
| 12 | + |
| 13 | +> 作者:我本张逸仙 |
| 14 | +
|
| 15 | +# 一. 变分推断 |
| 16 | + |
| 17 | +基本思路就是:在概率模型中,经常需要近似难以计算的概率分布。对于所有未知量的推断都可以看作是后验概率的推断(因为贝叶斯公式可以构造): |
| 18 | +$$ |
| 19 | +p(x) = \sum p(x|z)p(z) |
| 20 | +$$ |
| 21 | +对于大量数据而言,马尔可夫蒙特卡洛方法就太慢了,因此就需要用到**变分推断法**。 |
| 22 | + |
| 23 | +这里经常遇到的是两种变量,一个是**real data:$x$**,还有一个是**latent data: $z$**。 |
| 24 | + |
| 25 | +那么构造的推断问题就是:输入数据的后验条件概率分布$p(z|x)$的得知。通过**ELBO**的方法,希望找出一个**真实的分布$q(z)$**,用这个真实的分布来近似代替真实的**后验分布$p(z|x)$**。 |
| 26 | + |
| 27 | +因此需要优化的是它们的KL散度: |
| 28 | +$$ |
| 29 | +q^*(z) = argmin_{q(z)∈Q}KL(q(z)||p(z|x)) |
| 30 | +$$ |
| 31 | +而KL散度值也可以进一步改写:(下面的期望均是对$q(z)$的期望) |
| 32 | +$$ |
| 33 | +KL(q(z)||p(z|x)) =E(\log q(z)) - E(\log p(z|x))\\ |
| 34 | +=E(\log q(z)) - E(\log p(x,z)) |
| 35 | ++ \log p(x) |
| 36 | +$$ |
| 37 | +因此,定义**evidence lower bound(简称ELBO)**: |
| 38 | +$$ |
| 39 | +ELBO(q) = E(\log p(z,x)) - E(\log q(z)) |
| 40 | +$$ |
| 41 | +当然了,上面的$q(z)$可以换$q(z|x)$,那么等式只需要稍加修正一下即可: |
| 42 | + |
| 43 | +不论是在VAE,GAN还是在NF里面,总有一个不等式特别重要: |
| 44 | + |
| 45 | +- 让$p_\theta(z|x)$与$q_\phi(z|x)$尽可能近似 |
| 46 | + $$ |
| 47 | + D_{KL}(q_\phi(z|x)||p_\theta(z|x)) |
| 48 | + = \log(p_\theta(x)) - \sum_zq_{\phi}(z|x)\log(\frac{p_{\theta}(x,z)}{q_{\phi}(z|x)}) |
| 49 | + \\=\log(p_\theta(x)) - L(\theta,\phi;x) |
| 50 | + $$ |
| 51 | + 该方程想要$D_{KL}$尽可能接近于0,就是让他们俩个尽可能地接近,因此,继续做转换得到: |
| 52 | + $$ |
| 53 | + L(\theta,\phi;x) = E_{q_{\phi}(z|x)}[\log(p_{\theta}(x|z))] - D_{KL}(q_{\phi}(z|x)||p_{\theta}(z)) |
| 54 | + $$ |
| 55 | + 所以,把两个等式联立,就可得到: |
| 56 | + $$ |
| 57 | + \log(p_\theta(x)) - D_{KL}(q_\phi(z|x)||p_\theta(z|x)) = E_{q_{\phi}(z|x)}[\log(p_{\theta}(x|z))] - D_{KL}(q_{\phi}(z|x)||p_{\theta}(z)) |
| 58 | + $$ |
| 59 | + 而目标是要让$D_{KL}(q_\phi(z|x)||p_\theta(z|x))$尽可能接近于0,因此可以得到论文中的等式: |
| 60 | + $$ |
| 61 | + \log(p_\theta(x)) ≥ E_{q_{\phi}(z|x)}[\log(p_{\theta}(x|z))] - D_{KL}(q_{\phi}(z|x)||p_{\theta}(z)) = -F (x) |
| 62 | + $$ |
| 63 | + 上面的公式便是**变分推理**的重要的地方。这里的$F$被称为**ELBO**界 |
| 64 | + |
| 65 | +# 二. VAE (变分自编码器) |
| 66 | + |
| 67 | +VAE是想要上面求解的$ELBO$尽可能地大,它提出了SGVB和重参数方法。 |
| 68 | + |
| 69 | +VAE的网络架构图如下所示: |
| 70 | + |
| 71 | +<img src="https://tva2.sinaimg.cn/large/006UcwnJly1h55eci5870j30qb0gqjtb.jpg" style="zoom:50%;" /> |
| 72 | + |
| 73 | +简单来说,它是输入real data $x$,通过一个生成网络$h,g$生成想要得到的$\mu_x,\sigma_x$: |
| 74 | +$$ |
| 75 | +\mu_x = g(x) \\ |
| 76 | +\sigma_x = h(x) |
| 77 | +$$ |
| 78 | +再引入一个高斯噪声$N(0,1)$,两者相构造latent变量$z$(重参数技巧,这样可以反向传播了) |
| 79 | +$$ |
| 80 | +z = \sigma_x \zeta + \mu_x |
| 81 | +$$ |
| 82 | +然后$z$再通过decoder解码成$\hat{x}$: |
| 83 | +$$ |
| 84 | +\hat{x} = f(z) |
| 85 | +$$ |
| 86 | +注意:VAE在做的时候,要保证$z$是一个正态分布,因为这是它和AE一个很大的不同点,它能保证潜在空间是有一定的规律性-->连续性、完整性。 |
| 87 | + |
| 88 | +VAE的损失函数是: |
| 89 | +$$ |
| 90 | +L(\theta,\phi;x) = ELBO \\= |
| 91 | +E_{q_{\phi}(z|x)}[\log(p_{\theta}(x|z))] - D_{KL}(q_{\phi}(z|x)||p_{\theta}(z)) |
| 92 | +$$ |
| 93 | +这里的第一项可以理解为重构的损失,第二项可以理解为regularization loss |
| 94 | + |
| 95 | +用极大似然法去处理第一项,得到的答案就是: |
| 96 | +$$ |
| 97 | +(f^*,g^*,h^*) = argmax_{(f,g,h)∈F\times G \times H} (E_{z ~ q_x}(-\frac{||x-f(z)||^2}{2c}) - KL(q_x(z)||p(z))) |
| 98 | +$$ |
| 99 | +第二项怎么处理呢?直接积分求解即可: |
| 100 | +$$ |
| 101 | + - D_{KL}(q_{\phi}(z|x)||p_{\theta}(z)) = |
| 102 | + \int q_{\theta}(z)(\log p_{\theta}(z)-\log q_{\theta}(z))dz \\ |
| 103 | + = \frac{1}{2}\sum_{j=1}^J (1+\log((\sigma_j)^2)-\mu_j^2-\sigma_j^2) |
| 104 | +$$ |
| 105 | +(注意,因为是要尽可能使得$z$的分布接近于$N(0,1)$,因此$z$分布的均值是0,方差是1;而对于$q_{\phi}(z|x)$而言,它是$N(\mu,\sigma)$分布的)。 |
| 106 | + |
| 107 | +第二项的意思就是尽可能地让$q_{\phi}(z|x)$往$N(0,1)$上靠,第一项的意思就是生成的$\hat{x}$和$x$的MSE,第一项其实就是AE有的项;第二项就相当于一个正则化项。 |
| 108 | + |
| 109 | +如果你想要生成一个全新的图片的话,直接对$z$进行sampling,然后代入decoder网络,就可以得到一个全新的图片了。 |
| 110 | + |
| 111 | +# 三. GAN (对抗学习) |
| 112 | + |
| 113 | +GAN是一个生成器G--generator网络和一个判别器D-discriminator网络构成的: |
| 114 | + |
| 115 | +<img src="https://tva3.sinaimg.cn/large/006UcwnJly1h55efqdgjmj30rm0ckq5p.jpg" style="zoom:50%;" /> |
| 116 | + |
| 117 | +GAN可以认为是使用的是交叉熵的公式来判别分布的相似的: |
| 118 | +$$ |
| 119 | +H(p,q)=-\sum_{i}{p_i \log q_i} |
| 120 | +$$ |
| 121 | +这其实就像是一个二分类问题,数据要么从real data中得到,要么直接随机生成一个noise然后通过generator得到。那么discriminator就需要判断它到底是real还是fake的: |
| 122 | + |
| 123 | +discriminator就只说:对,错。就是一个二分类网络。 |
| 124 | + |
| 125 | +假定 ![[公式]](https://www.zhihu.com/equation?tex=y_1) 为正确样本分布,那么对应的( ![[公式]](https://www.zhihu.com/equation?tex=1+-+y_1) )就是生成样本的分布。 ![[公式]](https://www.zhihu.com/equation?tex=D) 表示判别器,则 ![[公式]](https://www.zhihu.com/equation?tex=D%28x_1%29) 表示判别样本为正确的概率, ![[公式]](https://www.zhihu.com/equation?tex=%EF%BC%881+-+D%28x_1%29%29) 则对应着判别为错误样本的概率。 |
| 126 | + |
| 127 | +因此用交叉熵来实现它就是: |
| 128 | + |
| 129 | +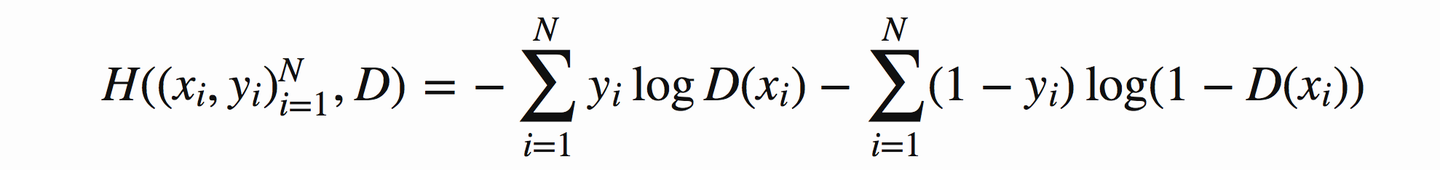 |
| 130 | + |
| 131 | +这里设生成器生成的样本$\hat{x}$~$G(z)$,$z$是服从于投入生成器中的噪声的分布。$x$是真实的样本点。 |
| 132 | + |
| 133 | +推广到无穷大,改写为积分形式。 |
| 134 | + |
| 135 | +下面是正式的流程: |
| 136 | + |
| 137 | +我们首先固定G(就是给一个任意的G),然后要得到的就是$V(G,D)$ |
| 138 | +$$ |
| 139 | +V(G,D) = \int _\infin p_{data}(x)\log D(x) dx + \int _\infin p_z(z) \log (1-D(g(z))) dz |
| 140 | +\\ = \int _\infin (p_{data}(x)\log(D(x)) + p_g(x)log(1-D(x)) )dx |
| 141 | +$$ |
| 142 | +然后对积分式里面的求导,就可以得到最大的$V(G,D)$,也就是此时$D$最牛逼了: |
| 143 | + |
| 144 | +此时: |
| 145 | +$$ |
| 146 | +D^*(x) = \frac{p_{data}(x)}{p_{data}(x)+p_g(x)} |
| 147 | +$$ |
| 148 | +即: |
| 149 | +$$ |
| 150 | +V(G,D) = E_{x->p_{data}}[ \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}]+E_{x->p_{g}}[ \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}] |
| 151 | +$$ |
| 152 | +然后此时又要不断的训练生成网络generator,让$\max_D V(G,D) = V(G,D^*)$最小:$C(G) = \min_G V(G,D^*)$ |
| 153 | + |
| 154 | +因此:当$p_g = p_{data} = 1/2$(纳什均衡,此时你可以认为它已经分不清楚谁是谁了)的时候,就得到了最小值了: |
| 155 | +$$ |
| 156 | +\min_G\max_D V(G,D) = \min_G V(G,D^*) = -\log 4 |
| 157 | +$$ |
| 158 | +此时,代入他们的最小值,改写: |
| 159 | +$$ |
| 160 | +C(G) = -log(4) + KL(p_{data}||\frac{p_{data}+p_g}{2})+ KL(p_{g}||\frac{p_{data}+p_g}{2}) \\= -log(4)+2JSD(p_{data}||p_g) |
| 161 | +$$ |
| 162 | +当JSD为0的时候,就认为$p_{data}$和$p_g$相等了,就分不出彼此来了。此时C* = -log4 |
| 163 | + |
| 164 | +# 四. NF (流模型) |
| 165 | + |
| 166 | +标准化流是另外一种生成网络,它基于一个空间变化的定理。 |
| 167 | + |
| 168 | +我们假设生成网络还是G,$z$是一个标准的正态分布--latent变量,而x是real data。 |
| 169 | +$$ |
| 170 | +Z->Generator...->x |
| 171 | +$$ |
| 172 | +因此希望生成的x的分布与x的初始分布越接近越好 |
| 173 | + |
| 174 | +假设$\{x^1,x^2,...,x^m\}$是来自$p_{data}(x)$的一个sampling |
| 175 | + |
| 176 | +希望$p_G(x)$与$p_{data}(x)$越接近越好,也就是有一个target: |
| 177 | +$$ |
| 178 | +G^* =argmax_G \sum_{i=1}^m \log P_G (x^i) |
| 179 | +\\≈ argmin_G KL (p_{data}(x)||p_G(x)) |
| 180 | +$$ |
| 181 | +这里有几个数学公式:**线性变换之后的体积**等于**转换矩阵的行列式** |
| 182 | + |
| 183 | +![[公式]](https://www.zhihu.com/equation?tex=y%3Df%28x%29%5C%5C+p%28y%29%3Dp%28f%5E%7B-1%7D%28y%29%29+%5Ccdot+%5Cleft%7C+%5Cdet%28J+%28f%5E%7B-1%7D%28x%29%29%29+%5Cright%7C+%5C%5C+%5Clog+p%28y%29%3D%5Clog+p%28f%5E%7B-1%7D%28y%29%29+%2B+%5Clog+%5Cleft%7C+%5Cdet%28J+%28f%5E%7B-1%7D%28x%29%29%29+%5Cright%7C+) |
| 184 | + |
| 185 | +也就是说,行列式可以被认为是变换 ![[公式]](https://www.zhihu.com/equation?tex=y%3Df%28x%29) 的**局部线性体积变化率** |
| 186 | + |
| 187 | +**NF的输入与输出的size必须相同**,这是与其他俩个不一样的,因为其他几个都是可以随意输入的。 |
| 188 | + |
| 189 | +然后假设它是一系列的Flow网络组成 |
| 190 | + |
| 191 | +<img src="https://tvax4.sinaimg.cn/large/006UcwnJly1h55esfn2mfj30y806i76i.jpg" style="zoom:50%;" /> |
| 192 | + |
| 193 | +因此对原网络进行修改: |
| 194 | +$$ |
| 195 | +\log p_K (x^i) = \log \pi(z^i) +\sum_{h=1}^K \log|det(J_{G_K^{-1}})| |
| 196 | +$$ |
| 197 | +要求左边等式的最大值-->log likelihood最大 |
| 198 | + |
| 199 | +那么要想求的话,可以反过来去考虑,通过x进入$G^{-1}$网络生成z。 |
| 200 | + |
| 201 | +由于上面那个式子的计算量太复杂了,因此需要做下面的处理: |
| 202 | + |
| 203 | +**1. Coupling Layer**: -- > 用在NICE 和 Real NVP里面的 |
| 204 | + |
| 205 | +<img src="https://tva2.sinaimg.cn/large/006UcwnJly1h55esr5szsj31bi0rzthl.jpg" style="zoom:40%;" /> |
| 206 | + |
| 207 | +它让前**1:d**的直接从z->x,而后边的**d+1:D**的就要通过前边的数据经过F和H网络求解$\beta_{d+1:D}$和$\gamma_{d+1:D}$,经过线性叠加: |
| 208 | +$$ |
| 209 | +x_{d+1:D} = \beta_{d+1:D} \times z_{d+1:D} + \gamma_{d+1:D} |
| 210 | +$$ |
| 211 | +而经过coupling layer后的贾克比矩阵就称为了一个三角矩阵: |
| 212 | + |
| 213 | + `<img src="https://gitee.com/thinker-jiang/markdown_pic/raw/master/markdown/20211024211939.png" style="zoom:50%;" /> |
| 214 | + |
| 215 | +因为上面的是直接copy过去的,就是1:1;而右下角的对角线上的值(D>i>d+1)就是$\beta_i$值 |
| 216 | + |
| 217 | +因此,贾克比矩阵的行列式即可写出: |
| 218 | +$$ |
| 219 | +det(J_G) = 1\times 1 \times ...\times 1\times \beta_{d+1}\times ...\times \beta_{D} |
| 220 | +$$ |
| 221 | +但是如果每一个网络都按照这样子去处理,那么是不是前d项都不会发生变化? |
| 222 | + |
| 223 | +因此必须要交错的去处理它,每一个网络随机选取d项,且d的大小也需要不一样,这样stacking起来后才会有效果。 |
| 224 | + |
| 225 | +<img src="https://tvax3.sinaimg.cn/large/006UcwnJly1h55et9ian9j30wy08gwhp.jpg" style="zoom:50%;" /> |
| 226 | + |
| 227 | + |
| 228 | + |
| 229 | +2. **1x1 Convolution** |
| 230 | + |
| 231 | +除了耦合层以外,还可以使用一维卷积,这个是GLOW提出来的,效果特别好。 |
| 232 | + |
| 233 | +假设是在处理图像,因此是有3个channels的,RGB三个通道嘛。用到的一维卷积就是一个3x3的矩阵$W$: |
| 234 | + |
| 235 | +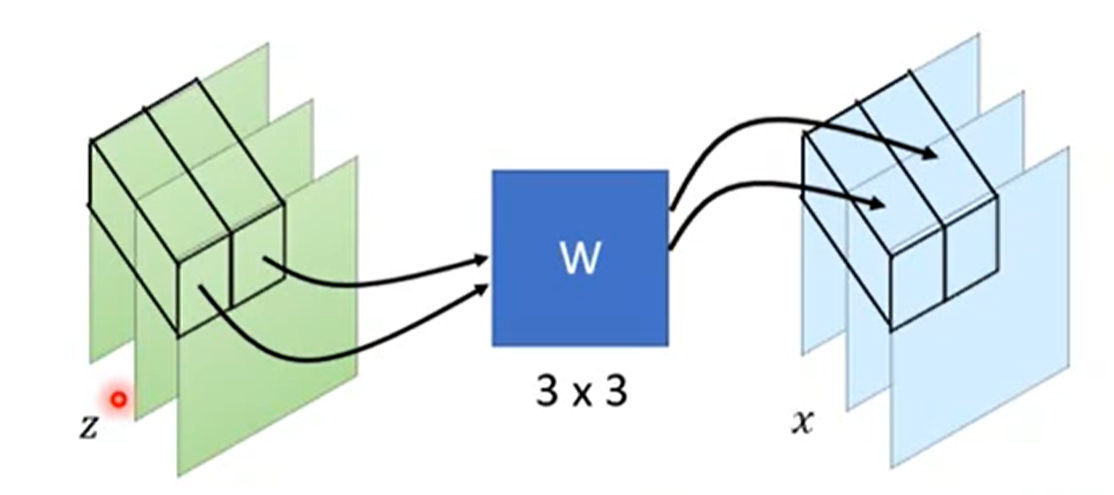 |
| 236 | + |
| 237 | +通过一维卷积后,size是不会发生变化的,而这个$W$矩阵其实就是$det(J_G)$: |
| 238 | +$$ |
| 239 | +x = f(z) =W\times z |
| 240 | +$$ |
| 241 | + |
| 242 | +$$ |
| 243 | +\begin{equation} %开始数学环境 |
| 244 | +J_f = \left( %左括号 |
| 245 | + \begin{array}{ccc} %该矩阵一共3列,每一列都居中放置 |
| 246 | + w_{11} & w_{12} & w_{13}\\ %第一行元素 |
| 247 | + w_{21} & w_{22} & w_{23}\\ %第二行元素 |
| 248 | + w_{31} & w_{32} & w_{33}\\ |
| 249 | + \end{array} |
| 250 | +\right) = W %右括号 |
| 251 | +\end{equation} |
| 252 | +$$ |
| 253 | + |
| 254 | +只要W是好求解的,那么结果也就很好求解: |
| 255 | + |
| 256 | +<img src="https://tvax4.sinaimg.cn/large/006UcwnJly1h55etopj8fj30v30gcwh4.jpg" style="zoom:50%;" /> |
| 257 | + |
| 258 | +因此结果就是,对角线上的W矩阵相乘: |
| 259 | +$$ |
| 260 | +(det(W))^{d\times d} |
| 261 | +$$ |
| 262 | +替换公式: |
| 263 | +$$ |
| 264 | +\log p_K (x^i) = \log \pi(z^i) +\sum_{h=1}^K \log|(det(W))^{d\times d}| |
| 265 | +$$ |
| 266 | +这样就将复杂运算简单化了 |
| 267 | + |
| 268 | + |
| 269 | + |
| 270 | + |
| 271 | +---- |
| 272 | +> 参考: |
| 273 | +[1] 李宏毅机器学习 |
| 274 | +[2] 苏剑林 |
| 275 | + |
0 commit comments