You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
2ab150c Removed toolchain specific warnings
0825d34 Adopted alternative implementation for lfs_ctz_index
46e22b2 Adopted lfs_ctz_index implementation using popcount
4fdca15 Slight name change with ctz skip-list functions
git-subtree-dir: littlefs
git-subtree-split: 2ab150c
Copy file name to clipboardExpand all lines: DESIGN.md
+86-10Lines changed: 86 additions & 10 deletions
Display the source diff
Display the rich diff
Original file line number
Diff line number
Diff line change
@@ -290,39 +290,40 @@ The path to data block 0 is even more quick, requiring only two jumps:
290
290
291
291
We can find the runtime complexity by looking at the path to any block from
292
292
the block containing the most pointers. Every step along the path divides
293
-
the search space for the block in half. This gives us a runtime of O(log n).
293
+
the search space for the block in half. This gives us a runtime of O(logn).
294
294
To get to the block with the most pointers, we can perform the same steps
295
-
backwards, which keeps the asymptotic runtime at O(log n). The interesting
295
+
backwards, which puts the runtime at O(2logn) = O(logn). The interesting
296
296
part about this data structure is that this optimal path occurs naturally
297
297
if we greedily choose the pointer that covers the most distance without passing
298
298
our target block.
299
299
300
300
So now we have a representation of files that can be appended trivially with
301
-
a runtime of O(1), and can be read with a worst case runtime of O(n logn).
301
+
a runtime of O(1), and can be read with a worst case runtime of O(nlogn).
302
302
Given that the the runtime is also divided by the amount of data we can store
303
303
in a block, this is pretty reasonable.
304
304
305
305
Unfortunately, the CTZ skip-list comes with a few questions that aren't
306
306
straightforward to answer. What is the overhead? How do we handle more
307
-
pointers than we can store in a block?
307
+
pointers than we can store in a block? How do we store the skip-list in
308
+
a directory entry?
308
309
309
310
One way to find the overhead per block is to look at the data structure as
310
311
multiple layers of linked-lists. Each linked-list skips twice as many blocks
311
-
as the previous linked-list. Or another way of looking at it is that each
312
+
as the previous linked-list. Another way of looking at it is that each
312
313
linked-list uses half as much storage per block as the previous linked-list.
313
314
As we approach infinity, the number of pointers per block forms a geometric
314
315
series. Solving this geometric series gives us an average of only 2 pointers
315
316
per block.
316
317
317
-
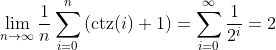
0 commit comments