spatial and temporal hierarchy

[hyunjimoon]

Tom and I had the temporal and spatial hierarchy discussion - red and green + korean and american rabbits and formulated three different cases as below:

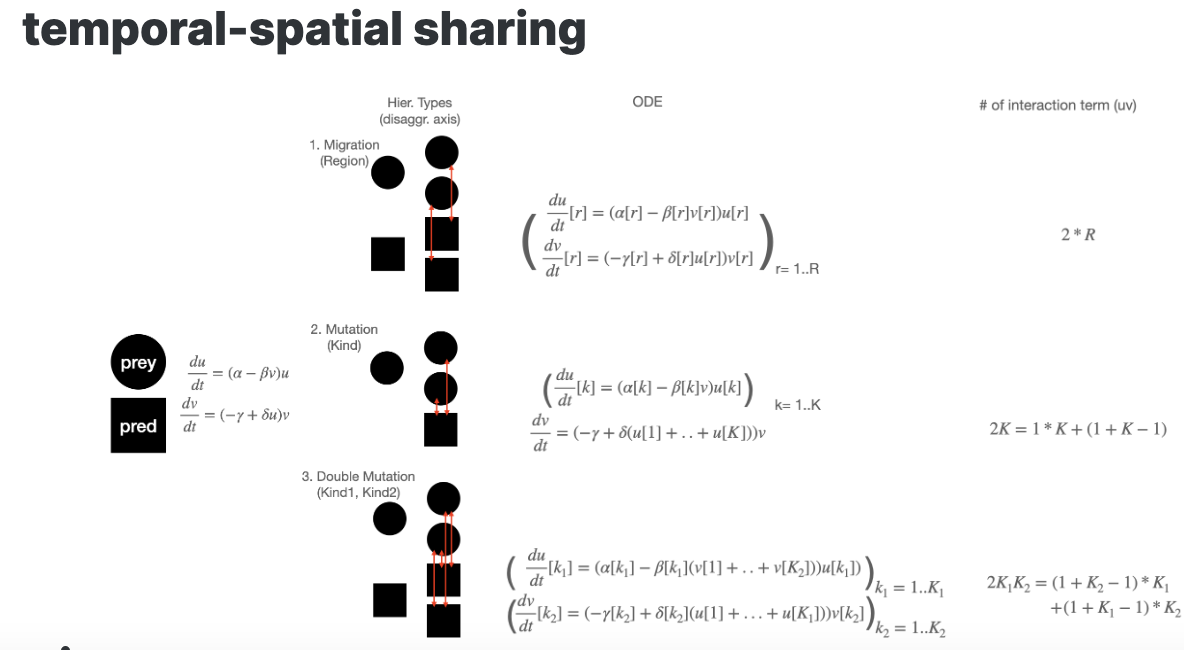
Stan-based pharma library may have templated this: https://metrumresearchgroup.github.io/Torsten/function/coupled/

By the way, this auto-generated file reflects the current status; I added time_step as having it as default 1 would be inaccurate.

From the talk on vaccine allocation, a generic temporal-spatial hierarchical frame + solution mechanism seems needed. We can't apply taylor approximation + analytic solution for every problem out there (which was Isabelle's approach). Most of the discussion was on what order the solution is (holomorphic..) but given the uncertainty of the model itself (SIR) I wonder how much practical value this can have. That being said, LP, QP, SDP formulation for vensim simulation model can be useful. [Path finder](https://statmodeling.stat.columbia.edu/2021/08/10/pathfinder-a-parallel-quasi-newton-algorithm-for-reaching-regions-of-high-probability-mass/), new fast and stable approximate algorithm that can also supply starting points for HMC, may be relevant.

Isabelle Rao, Presenting Optimal Responses to Epidemics: Models to Support Good Decisions

Abstract
Policy makers make consequential choices about how to allocate limited resources to improve population health. My research aims to find avenues to optimize the use of these resources. The first part of my talk addresses the problem of how to optimally allocate limited vaccines to control the spread of an infectious disease. This problem is dynamic, nonlinear and stochastic, and is typically solved numerically. By approximating the epidemic dynamics, I am able to develop simple analytical conditions characterizing the optimal vaccine allocation for four different objectives. The approximated solution is an all-or-nothing allocation based on a prioritized list of population groups given by the analytical conditions. This provides a practical and intuitive tool for decision makers as they allocate vaccines over time. I illustrate my method with an example of COVID-19 vaccination, calibrated to epidemic data from New York State. Numerical computations show that my method achieves near-optimal results over a wide range of scenarios. Although black-box models are prevalent in the literature, this work shows that accuracy need not be sacrificed for interpretability.

In the second part of the talk, I present a dynamic model to assess the effectiveness of interventions for controlling the US opioid epidemic. I show that reductions in opioid prescriptions are necessary but may lead to a short-term increase in heroin overdose deaths, and thus must be combined with scale up of treatment for addicted individuals -- but that even with immediate policy changes, significant morbidity and mortality will still occur. This project informed the work of the Stanford-Lancet Commission on the North American Opioid Crisis, and provides critically needed evidence-informed recommendations for reducing opioid-related morbidity and mortality in the US.