📦 Zipping casual loop as lookup or inter-dependent fraction from coflow structure #38
Replies: 8 comments 8 replies
-
Beta Was this translation helpful? Give feedback.
-
|
I'm not following how conjugate priors help here. Is the screening function for detecting the problem, or something else? In any case, I'm not sure I agree that fineness of time scale is the origin of the aggregation problem. Consider the following thought experiment. Red and blue people go to a bar. They arrive at a uniform rate, or stationary random rate if you prefer. Once in the room, they mingle with others. After an exponentially-distributed time they leave. This is basically the classic first-order well mixed system. Suppose we're interested in the average wealth in the bar, and reds have twice as much money as blues. Then we could measure the flow of colors on the way in the door and infer the average stock from that. This can go wrong in several ways.
#1 implies that the first-order structure is wrong both in aggregate and for any individual agent. You need an aging chain or pipeline delay, or maybe a spatial grid, to represent the process. #2 implies that you need to disaggregate by color (but you can keep the first-order assumption). #3 probably requires disaggregation by color, and some additional feedback among the colors that varies the residence time according to the fight behavior. I'm not sure any of these is directly related to the time scale, except in the sense that some of these behaviors may be too fine-scaled for us to care about if the model horizon is long. For example, in case #3, if we're modeling the bar's financial health over 10 years, we don't care about the high frequency behavior of bar fights and color distinctions. We could just roll that into a slightly shorter aggregate time constant. But if we're modeling a night, or even a month, we probably do care about these details. When I hear "fineness of time scale cannot allow well mixing" I think of a literal mixing problem. The bar is full of blue people. 10 reds enter through the door. After a couple of minutes, you have reds and blues mingled. But one second after the reds enter, they're probably still in a clump by the door. Does this matter? Maybe - it depends again on the time horizon of interest for the model, and whether the temporary spatial clumping initiates any nonlinear processes that are important enough to require disaggregation. |
Beta Was this translation helpful? Give feedback.
-
|
Design convention enforcing temporal cauchy convergence w.r.t. time steps (halve ts until stock values(ts) ~ stock values(ts/2)) but not space step (i.e. subscript) is the source of the problem. May I summarize your setting as: measuring quantities red and blue differs (f(theta1, theta2,t); not f(theta,t))? Two comments:
@tomfid I wish to at least get your consent on random variable ~ lookup function recalling our distribution function discussion last week. This needs justification but 'Time scale' seems to be the finest lego block we build for calculus system (Lebesgue integral). "fine enough time step?" is the other side of "Long enough time horizon?" question as we want compact (closed and bounded) integral interval and once it is compact we can scale it without losing any info.
red and blue ppl: "After an exponentially-distributed time they leave. This is basically the classic first-order well mixed system". As long as we measure |
Beta Was this translation helpful? Give feedback.
-
I think the point about easy enforcement of temporal convergence is insightful. I think it's a consequence of the language architecture - time can be changed globally with a switch, but space, aging chain order, red/blueness, etc. require manual labor to change subscripts typically. It would be interesting to think through a simple way of expressing something more flexible. Attribute coflows are also something that could be automated, but isn't. |
Beta Was this translation helpful? Give feedback.
-
|
SD's logistic choice forumation is similar to dirichlet process's prior SDBayestheta_j = exp(phi_j)/(exp(phi_1)+exp(phi_2)+exp(phi_3)+exp(phi_4) suggested as answer to "priors to dirichlet prior" in Gelblog and equation 1 from his paper "Pharmacokinetic Analysis using population modeling and informative prior distributions". Sec.2.3 has great info on prior dist.
20220710_Sust_Consumption_ISDC 2022_Poster_v02.pdf |
Beta Was this translation helpful? Give feedback.
-
|
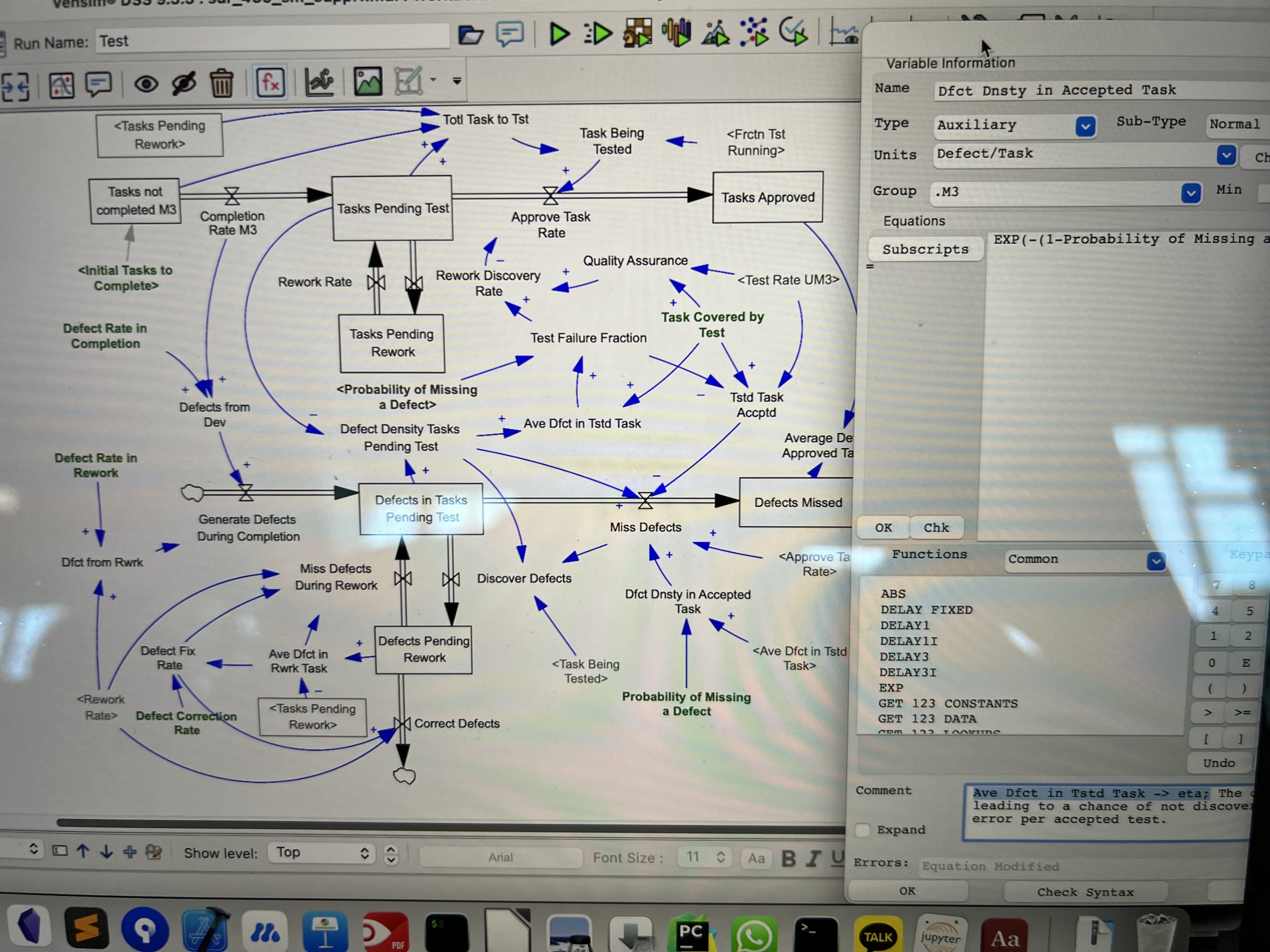
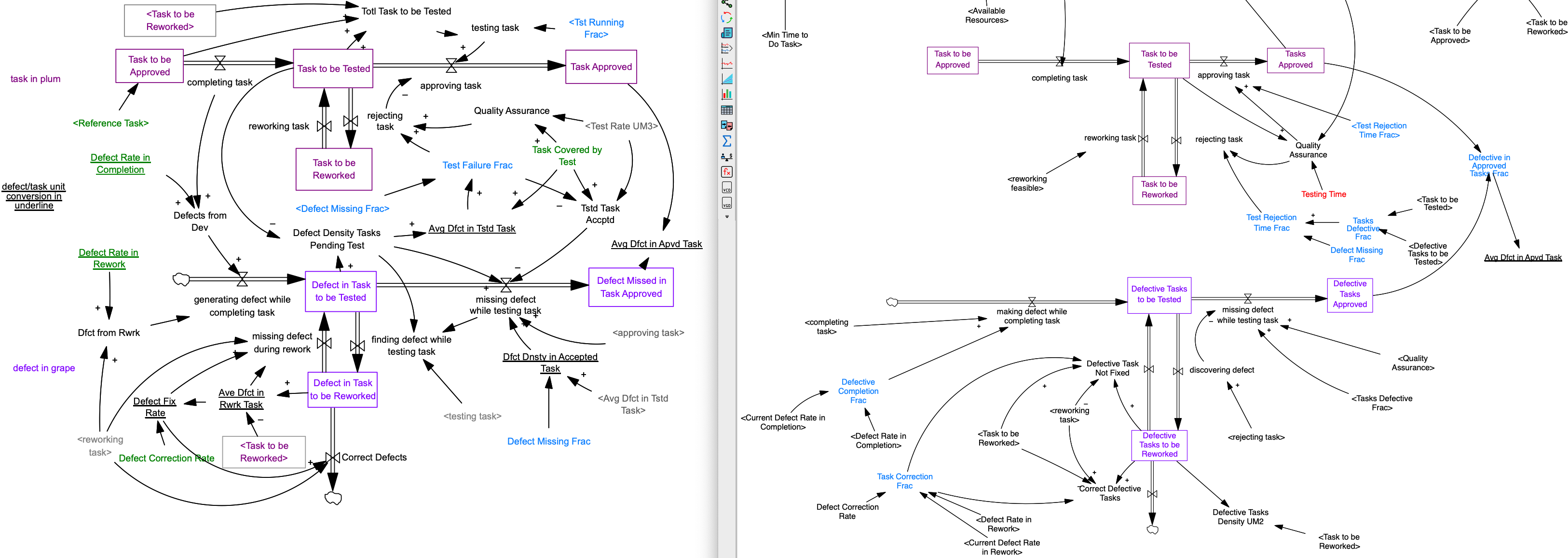
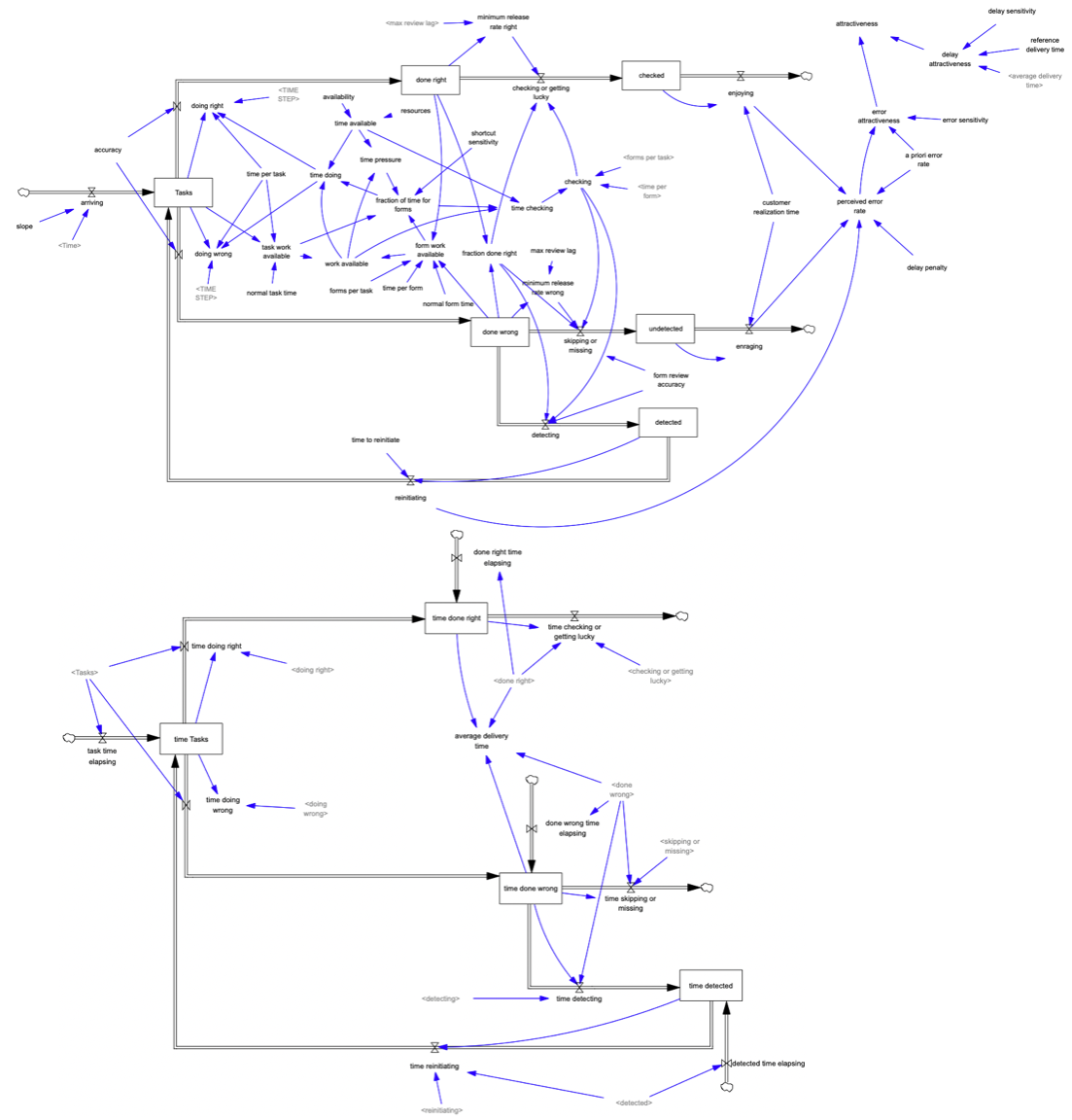
For some reason Hazhir updated the coflow units (from left to right) and I wonder whether the right version is more communicable. first version has different unit for coflow (task for the above, defect for below), but recent Hazhir's version improved(?) this by using the same unit, naming the conditioned coflow |
Beta Was this translation helpful? Give feedback.
-
Beta Was this translation helpful? Give feedback.
-
|
I think this book published today would be relevant to our conjugate prior design: During the past half-century, exponential families have attained a position at the center of parametric statistical inference. Theoretical advances have been matched, and more than matched, in the world of applications, where logistic regression by itself has become the go-to methodology in medical statistics, computer-based prediction algorithms, and the social sciences. This book is based on a one-semester graduate course for first year Ph.D. and advanced master's students. After presenting the basic structure of univariate and multivariate exponential families, their application to generalized linear models including logistic and Poisson regression is described in detail, emphasizing geometrical ideas, computational practice, and the analogy with ordinary linear regression. Connections are made with a variety of current statistical methodologies: missing data, survival analysis and proportional hazards, false discovery rates, bootstrapping, and empirical Bayes analysis. The book connects exponential family theory with its applications in a way that doesn't require advanced mathematical preparation. |
Beta Was this translation helpful? Give feedback.

Uh oh!
There was an error while loading. Please reload this page.
Uh oh!
There was an error while loading. Please reload this page.
-
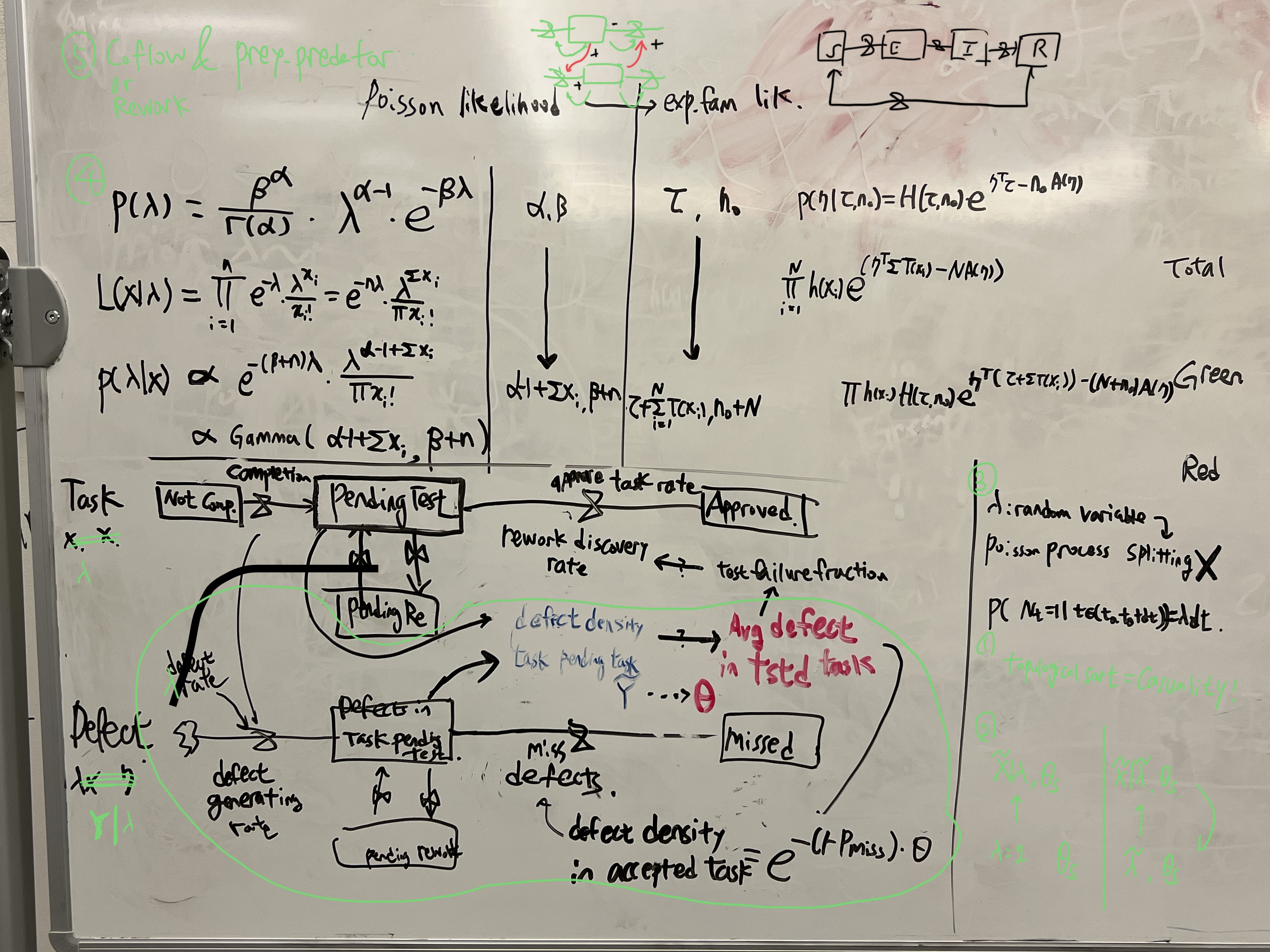
Research hypothesis: When the desired fineness of time-scale cannot allow well-mixing of one compartment, conjugate function (defined as the same distributional family of prior and posterior) can be used for screen function.
Jose delved into exponential family for this, which I assume to be relevant to the fact conjugate prior can be designed for every exponential families "For exponential families the likelihood is a simple standarized function of the parameter and we can define conjugate priors by mimicking the form of the likelihood.".
The next step may be implementing exponential family on Hazhir's rework model. I uploaded initial points in conjugacy folder in conjugacy brach https://github.com/Data4DM/BayesSD/tree/conjugacy, https://github.com/Data4DM/BayesSD/tree/conjugacy/ContinuousCode/5_BayesCalib/experiment/conjugacy.
Beta Was this translation helpful? Give feedback.
All reactions