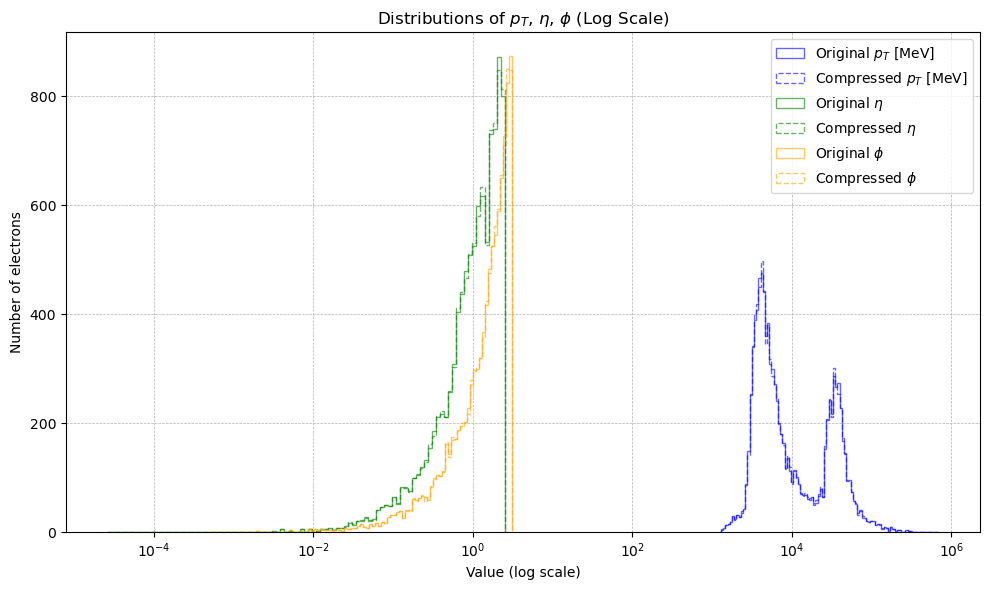
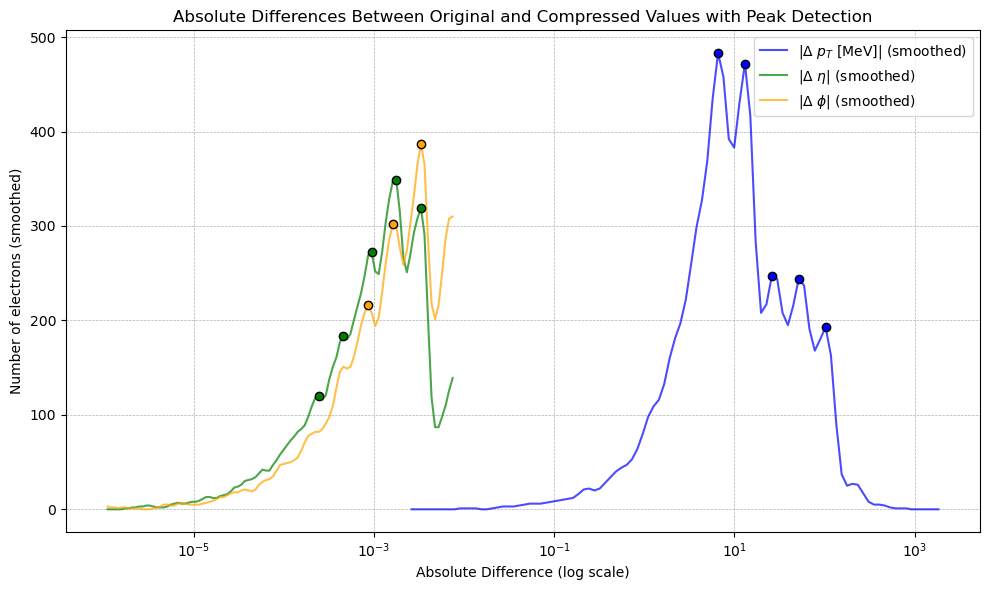
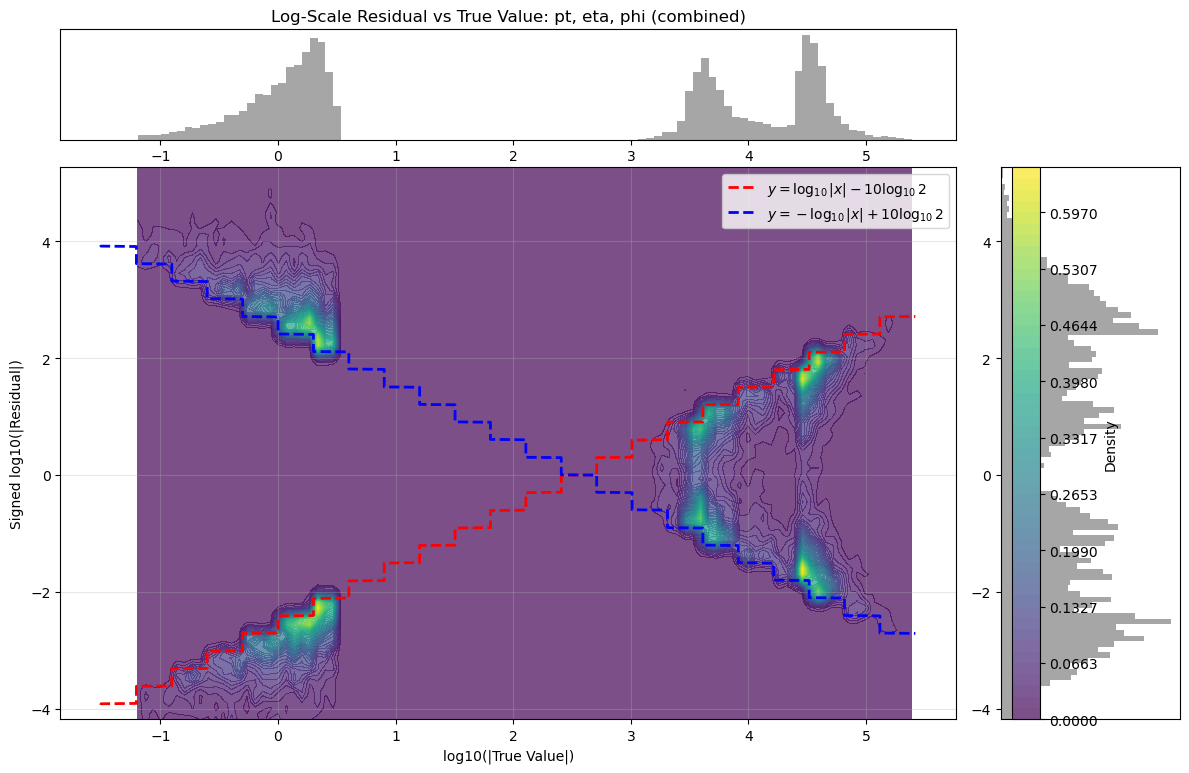+ 
+
+
+
+
+
+This represented the core theoretical output of the project. We found such regular, stepped patterns in the residual in all truncated float data which we understood was likely some generalised quantisation error that occurs due to discarding $n$ bits. The next step was then to rigorously derive the actual mechanism by which the residual changes based on the truncation amount. This theoretical model had not been found in literature in specifics, so this was a particularly exciting outcome. The full derivation can be found [here](https://github.com/yolannel/ATLAS_decompression/blob/master/theoretical_quantisation_bounds.md), with the model as follows:
+
+* **Final symmetric bounds**:
+
+ $\log_{10} |\Delta|_{\text{signed}} \in
+ \left[
+ -\log_{10}|x| + m\log_{10}(2), \;\; \log_{10}|x| - m\log_{10}(2)
+ \right]$
+
+ * These bounds form **two diagonal lines** on a log-log plot of $\log_{10}|x|$ vs. $\log_{10}|\Delta|$.
+ * Slopes: $\pm 1$.
+ * Vertical intercepts: determined by $m\log_{10}(2)$.
+ * The step-like function seen in real valued data has step sizes of approximately $\Delta \log_{10} \approx 0.28 \;\Rightarrow\; \text{ratio} \approx 1.9$, as in the peak spacing before.
+
+As a result, the project diverged slightly to explore how we can appropriately leverage this theoretical model to target any reconstruction of the remaining bits to quantisation error, rather than a blanket recovery.
+
+
+
+The current work in progress attempts to use the previously defined probabilistic models to model the distribution of data in varying ways, for which the residual can then be calculated and compared to the theoretical maximum and minimum bounds to determine how likely the residuals are to be due to quantisation. This hybrid approach is designed to minimize 'hallucinations' in the precision upsampling pipeline which could discard or modify important anomalies which can occur and are of particular interest in HEP data.
+
+As a part of exporatory work, I have implemented autoencoders, variational autoencoders, and flow matching models to successfully reconstruct the distributions of the data of interest (currently, the momentum, eta, and phi of electrons as a minimal test set), demonstrating that such models are sufficiently complex to capture the characteristics of the data. These models also carry additional benefits such as retrievable statistical characteristics and densities, which could benefit downstream usage.
+
+In the context of the proposed pipeline, I had first attempted to train an autoencoder (taking the implest model to create a 'minimum viable product', as it were) under a denoising workflow wherein I have as input to the model the compressed data, optionally with some added noise. The output of the model, then, is trained to be the 'denoised' data (where if no noise was added, one can consider the mantissa truncation to add 'quantisation noise') and MSE loss is taken of the model output versus the original, uncompressed data. The addition of some small amount of Gaussian noise is a common technique which I use in my day-to-day work and can often encourage the model to learn more effectively. Models at this scale are easily and quickly trained on an NVIDIA RTX4080, with 100 epochs taking on average ~15 minutes, or during testing, converging sufficiently within 30 epochs to establish a rough performance measure. All models were implemented using pytorch, with additional functionalities used for evaluation using scikit-learn statistics and numpy operations where necessary.
+
+Another approach under development is to treat the data as an inpainting problem, commonly seen within image generation where some part of an image may be blacked out; an inpainting model is designed to "fill in the blanks". In our case, we not only have the new theoretical bounds but also the first $23-n$ bits of data that is retained after truncation: this is valuable information which, in statistical tests, is also often a 'good-enough' approximation of the uncompressed data to begin with. Then, the challenge is only to "fill in" the remaining truncated $n$ bits which represents an even more bounded problem space and would minimize unexpected upsampling artifacts by constraining any correction terms to be within the allowable $n$ bits of change.
+
+While this project has not yet conclusively found a candidate model to precision upsample, ongoing work is being performed and is to continue beyond the timeline of the GSoC project toward proposing a working pipeline based off of the work performed up to this point. In short, autoencoders, variational autoencoders, and some simple flow matching models have been implemented and tested, with performance measured using simple MSE loss as well as distribution-based metrics such as KL divergence. The pipeline of the model was being tested in Jupyter notebook files, but I have begun to move them to modular python files to facilitate further work.
+
+## My thoughts on GSoC
+
+I had first approached my mentors and this project with the excitement of applying some of my current research in generative models for scientific machine learning directly to this precision upsampling problem, drawing parallels between "making the numbers more precise" and "superresolving medical images", for example. However, despite the extensive data exploration we performed and the theoretical work I ended up doing stalling the work directly applying deep learning models to these PHYSLITE file data, I found it both satisfying in being able to derive a clear reason to the phenomena I observe in the data but also extremely informative in terms of designing (as a work in progress) a more rigorous deep learning system. I have also had the opportunity to present my work to the S&C group, which generated some useful discussion which I look forward to applying to my work, and will be further presenting it during the ATLAS S&C Week workshop in the fall.
+
+Working on HEP data was both fascinating from the subject matter but also in terms of the problem area being tackled, and I hope that my continued work can benefit not only this specific upsampling target for PHYSLITE data, but lossy compression as a whole. My time working with my mentors was fruitful and inspiring, and I felt integrated into the group via group meetings and the strong support that both mentors provided throughout the project. I am thankful for such an exciting opportunity as well as my mentors' insightful feedback each week, and I look forward to continuing my work beyond this summer with them!
\ No newline at end of file