finish intro

Author: allensctong

class15/class15.jl

@@ -37,40 +37,62 @@ md"""
 md"""
 ## Chapter Outline
 
-- Transients and Transient Stability Constrained Optimal Power Flow (TSC-OPF) problem
-- Generator swing equations
-- Inverters
-- Dynamic load models
+This chapter motivates the need for optimization and control of power systems by introducing the **Economic Dispatch (ED)** and **Optimal Power Flow (OPF)** problems and analyzing the physical behaviors they capture in power system.
+ 
+We progressively move from solving *static optimization* problems to augmenting them with *dynamic optimal control* constraints as approaches to analyze and understand power systems.
+
+**Topics covered:**
+- **Transients and Transient Stability–Constrained OPF (TSC-OPF):**  
+  What are transients, their physical behaviors, and how they are factored into stability analysis of energy systems via the TSC-OPF formulation.
+
+- **Generator Swing Equations:**  
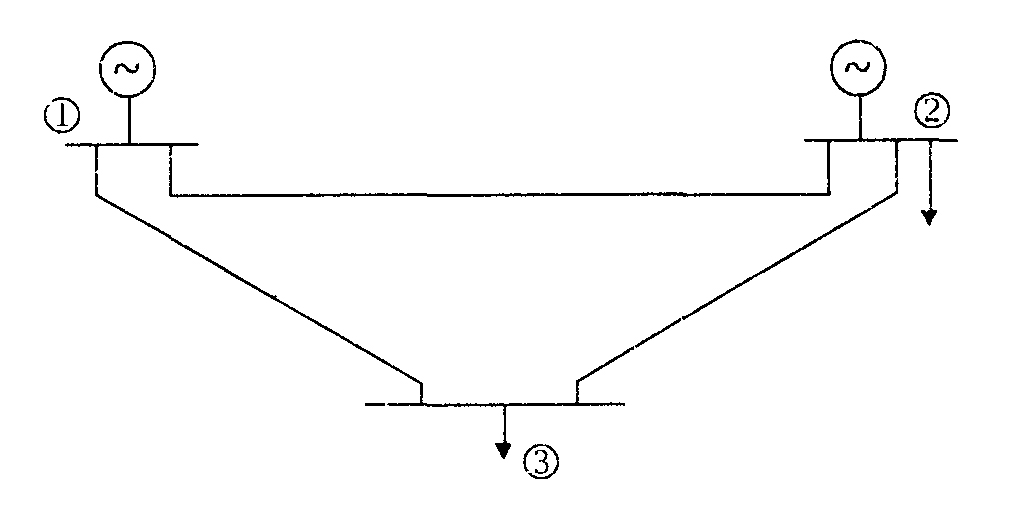
+  The physical foundation of synchronous machines — describes how mechanical torque and electrical power control frequency and machine responses to frequency changes.
+
+- **Inverter Control Models:**  
+  Grid-following vs. grid-forming inverters, and how virtual inertia control emulates synchronous generator dynamics for renewables.
+
+- **Dynamic Load Models:**  
+  Representations of demand that vary with voltage and frequency instead of a fixed a quantity, influencing both stability and control.
+
+> 🧭 **Overall goal:**  
+> To connect steady-state optimization (ED/DC-OPF) with **dynamic optimal control**, illustrating how classical control laws and physics-based constraints shape modern power system operation.
 """
 
 # ╔═╡ f742f5f3-d9d3-4374-ac9e-17073c3a2f6d
 md"""
 # Introduction to Energy Systems
-## Economic Dispatch
+## From Economic Dispatch to Dynamic Optimal Control
 
-To illustrate the fundamental concepts and problems in power system, we start with a simple economic dispatch (ED) problem on a 3-bus network.
+Optimal control of power systems builds on static optimization formulations like *economic dispatch* (ED) and *optimal power flow* (OPF).  
+These problems provide the mathematical foundation for **transient stability–constrained OPF (TSC-OPF)** formulations covered later in this chapter.
 
+To illustrate the key ideas, we start with the simplest case — the economic dispatch problem on a 3-bus system.
+
+**Example:**
 - Bus 1 load: 50 MW  
 - Bus 3 load: 75 MW  
-- Generator 1: Capacity 100 MW, Cost \$8/MW  
-- Generator 2: Capacity 40 MW, Cost \$2/MW  
+- Generator 1: capacity = 100 MW, cost = \$8/MW  
+- Generator 2: capacity = 40 MW, cost = \$2/MW  
 
 ![3-Bus Power System Network](https://www.al-roomi.org/multimedia/Power_Flow/3BusSystem/SystemIII/Murty3BusSystem.jpg)
+
+**Goal:** Minimize total generation cost while meeting total demand — the simplest form of *static* optimal control in power systems.
 """
 
+
 # ╔═╡ ad8e9d79-e226-468e-9981-52b7cda7c955
 md"""
 ### Quadratic Program (QP) Formulation of Economic Dispatch
 
-The economic dispatch problem can generally be formulated as a quadratic program. A generic ED formulation is:
+Economic dispatch can be formulated as a **quadratic program**, where generation cost is convex and constraints balance supply and demand conditions.
 
 ```math
 \begin{align}
 \min_{p_g} \quad & \sum_{g \in \mathcal{G}} C_g(p_g) \\
 \text{s.t.} \quad & \sum_{g \in \mathcal{G}} p_g = \sum_{d \in \mathcal{D}} P_d \quad \text{(power balance)} \\
-& p_g^{\min} \leq p_g \leq p_g^{\max} \quad \forall g \in \mathcal{G} \quad \text{(capacity bounds)}
+& p_g^{\min} \le p_g \le p_g^{\max}, \quad \forall g \in \mathcal{G} \quad \text{(capacity limits)}
 \end{align}
-```
+
 
 
 where:
@@ -86,14 +108,16 @@ where:
 
 # ╔═╡ fc329e51-e91c-4d83-b6fe-07a3bce44d5d
 md"""
-### Exercise: Formulate the ED problem for the 3-bus network
+### Exercise: Formulate the ED Problem for the 3-Bus Network
 
-Now let's apply this formulation to our 3-bus example. Using the 3-bus system above (with loads and cost data), write down:
+**Task:**  
+Apply the generic formulation to the 3-bus system. Identify:
+1. The decision variables  
+2. The objective function  
+3. The power-balance constraint  
+4. Generator bounds
 
-- The decision variables  
-- The objective function  
-- Power-balance constraint  
-- Generator bounds
+> 💡 *Hint:* Treat each generator’s output as a controllable decision variable. The total generation must exactly match total load.
 """
 
 # ╔═╡ d767175f-290d-403e-99de-d3a8f2ccb5b5
@@ -115,57 +139,65 @@ Here is the complete formulation for our 3-bus example:
 - Total cost: 8*85 + 2*40 = 760\$/hour
 - Gen 2 at maximum capacity (greedy)
 - Gen 1 supplies remaining demand
+
+> ⚙️ Control Interpretation: This is a static control allocation problem. In later sections, we’ll extend such formulations to time-varying states and control trajectories.
 """
 
 # ╔═╡ c9d0e1f2-0894-4340-a18b-72f8e1204432
 md"""
-### Discussion Questions
+### Discussion
+
+Reflect on the ED formulation:
 
-Before moving forward, let's reflect on what we've learned. What do you observe from your formulation?
+- What type of optimization problem is this (linear, quadratic, convex)? 
+- How does this formulation abstract away the **physical grid topology**? What kind of graph is it?
+- What critical physics are missing if we care about **how** power moves through lines?
 
-- What kind of problem is this (linear, quadratic, etc.)?
-- The power network is a graph -- what type? What is missing here?
-- The flow is not controllable - we did not place branch constraints.
+> 🧭 **Bridge to next topic:**  
+> ED models the **steady-state optimization** problem without considering power flow through lines.
+> The next step — **DC power flow** — adds physical coupling constraints between buses.
 """
 
 # ╔═╡ 9d1ea9be-2d7b-4602-8a8e-8426ea31661a
 md"""
-### What's the Problem?
+### Why the Simplified Model Falls Short
 
-The simple ED formulation we've seen has several limitations that become apparent when we consider the physical reality of power systems:
-
-- The graph should be directed: power has flow directions
-- Line ratings and safety are ignored in ED
-- Overloading lines is dangerous (thermal expansion, sag, wildfire risk)
+The simple ED model ignores the **network physics** that govern actual power transfer:
+- Power has **direction** — it flows through transmission lines governed by voltage phase angles so the graph needs to be directed.
+- Each line has a **thermal rating**: excessive current causes heating, sagging, or even wildfires.
 - What is a power line:
-  - Metal coil that expands and heats up when current is higher.
-  - That's why we have rating (magnitude of power flow cannot exceed this amount). Physically you can exceed it (nothing is preventing the power to flow) a bit, but there are consequences above ...
-- We need branch (line) constraints to ensure safe operation
+  - Metal coil that expands and heats up when current is high.
+
+In real systems, exceeding thermal limits does not immediately stop power flow — it simply becomes unsafe, which requires branch flow constraints.
+Thus, the next layer of realism is to introduce branch constraints → **DC power flow**.
 """
 
 # ╔═╡ 71ba62e6-bcc1-4e9b-91cd-a8860ba0d2b5
 md"""
 ## DC Power Flow
 
-To address these limitations, we extend the ED formulation to include network constraints through DC power flow. This formulation accounts for power flow directions and line limits.
+To make ED more realistic, we include the grid’s topology by adding branch constraints.
+The **DC power flow model** provides a linearized approximation of AC power flow and enforce Kirchhoff’s laws.
 
-**Data:**
+**Parameters:**
+- Line reactance $x_{ij}$
+- Line limit $F_\ell^{\max}$
 - Generator set $\mathcal{G}_i$ at bus $i$ (nodal generation)
 - Load set $\mathcal{L}_i$ at bus $i$ (nodal load)
+- Generator limits $P_j^{\min}, P_j^{\max}$
 - Costs $C_j(P_j)$ quadratic or piecewise-linear for generator $j$
-- Line limits $F_\ell^{\max}$, generator bounds $P_j^{\min}, P_j^{\max}$
 
-**Decision variables:**
+**Decision Variables:**
 - Generator outputs $P_j$ for $j \in \mathcal{G}_i$
 - Bus angles $\theta_i$ for $i \in \mathcal{N}$
 - Line flows $f_\ell$ for $\ell \in \mathcal{L}$
+
+> 🧩 We will see later that the bus angles $\theta_i$ enter as *state variables* in the control dynamics.
 """
 
 # ╔═╡ 7b4800c2-133d-4793-95b1-a654a4f19558
 md"""
-### DC Power Flow Formulation
-
-The DC power flow optimization problem combines economic dispatch with network physics:
+### DC Optimal Power Flow Formulation
 
 ```math
 \begin{align}
@@ -177,20 +209,20 @@ The DC power flow optimization problem combines economic dispatch with network p
 \end{align}
 ```
 
-- Reactance of line $x_{ij}$. $\frac{1}{x_{ij}} = b_{ij}$: susceptance (manufacturer specified)
-- Reference bus: only for modeling, you can pick any bus as the reference bus. We only care about angle differences (which carries current through lines
+- Reactance of line: $x_{ij}$. $\frac{1}{x_{ij}} = b_{ij}$: susceptance (specified by equipment manufacturer)
+- Reference bus: only for modeling, you can pick any bus as the reference bus. We only care about angle differences (which carries current through lines)
 - Individual bus angle has no physical meaning
 """
 
 # ╔═╡ 7961c1d1-3e82-49ea-8201-c5f82066d70d
 md"""
-### Exercise: Solve DCOPF (solver suggested: Ipopt)
+### Exercise: Solve DCOPF (suggested solver: Ipopt)
 
-Let's apply the DC power flow formulation to our 3-bus network with line constraints:
+Let's apply the DC power flow formulation to the 3-bus network with line constraints:
 
 ![3-Bus Network with Constraints](https://www.al-roomi.org/multimedia/Power_Flow/3BusSystem/SystemIII/Murty3BusSystem.jpg)
 
-**How did I get the numbers:**
+**Net generation calculations:**
 - Assume P1 generates 85 MW, with 50 MW of load, the net injection is 35 MW
 - Assume P2 generates 40 MW, with no load, net injection is 40 MW (we take upwards arrow as injection)
 - Bus 3 has no gen, only load
@@ -200,7 +232,7 @@ Let's apply the DC power flow formulation to our 3-bus network with line constra
 md"""
 ### DCOPF Solution
 
-Consult lecture slides for the solution and detailed analysis.
+Consult lecture slides for the solution and detailed analysis. Observe how adding line limits changes dispatch and total cost.
 """
 
 # ╔═╡ f72775b9-818c-4a9b-9b66-cfccd88e17ed
@@ -209,9 +241,10 @@ md"""
 
 This section has introduced the fundamentals of static optimal power flow problems including economic dispatch and DC optimal power flow. Key takeaways:
 
-- You will see that without thermal limits, optimal dispatch can overload lines
-- Reference bus is arbitrarily picked by the solver.
-- Real systems are AC (complex voltages/currents) -- much harder. This is just a lightweight intro so we can think about expressing real-world problems as optimization formulations without overburdening ourselves with AC physics, which we will see in transient stability section.
+- You observed that without thermal limits, optimal dispatch from ED can overload lines
+- Real systems are AC (complex voltages/currents) -- much harder. This is just a lightweight intro so we can think about expressing real-world problems as optimization formulations without burdening ourselves with AC physics, which we will see in transient stability section.
+
+In the next section, we introduce transients and transient stability constraints to capture dynamic states of grid components, bringing time domain dynamics into the optimization.
 """
 
 # ╔═╡ 53ab9b31-78aa-49b6-9e24-df47aa80f25a