|
| 1 | +# 局部加权线性回归(Locally weighted linear regression) |
| 2 | + |
| 3 | +假如问题还是根据从实数域内取值的 $x\in \mathbb R$ 来预测 $y$ 。左下角的图显示了使用 $y = \theta_0 + \theta_1x$ 来对一个数据集进行拟合。我们明显能看出来这个数据的趋势并不是一条严格的直线,所以用直线进行的拟合就不是好的方法。 |
| 4 | + |
| 5 | +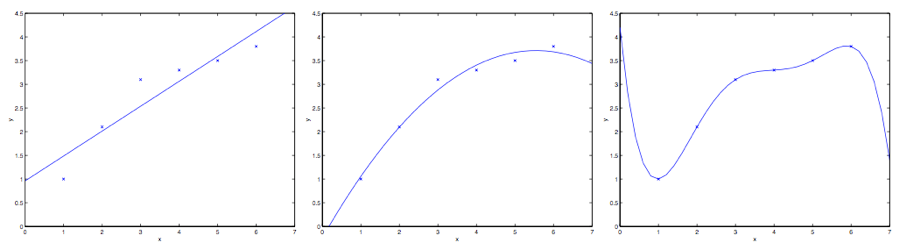 |
| 6 | + |
| 7 | +那么这次不用直线拟合,增加一个二次项,用二次多项式 $y = \theta_0 + \theta_1x +\theta_2x^2$ 来拟合。(看中间的图) 很明显,我们对特征补充得越多,效果就越好。 |
| 8 | + |
| 9 | +不过,增加太多特征也是有风险的:最右边的图就是使用了五次多项式 $y = \sum^5_{j=0} \theta_jx^j$ 来进行拟合。看图就能发现,虽然这个拟合曲线完美地通过了所有当前数据集中的数据,但我们明显不能认为这个曲线是一个良好的预测工具。最左边的图像就是一个**欠拟合 (under fitting)** 的例子,明显能看出拟合的模型漏掉了数据集中的结构信息;而最右边的图像就是一个**过拟合(over fitting)** 的例子。(当我们讨论到关于学习理论的时候,会给出这些概念的标准定义,也会给出拟合程度对于一个猜测的好坏检验的意义。) |
| 10 | + |
| 11 | +正如前文谈到的,也正如上面这个例子展示的,一个学习算法要保证能良好运行,特征的选择是非常重要的。(等到我们讲模型选择的时候,还会看到一些算法能够自动来选择一个良好的特征集。)在本节,咱们就简要地讲一下局部加权线性回归(locally weighted linear regression ,缩写为LWR),这个方法是假设有足够多的训练数据,对不太重要的特征进行一些筛选。 |
| 12 | + |
| 13 | +在原始版本的线性回归算法中,要对一个查询点 $x$ 进行预测,比如要衡量$h(x)$,要经过下面的步骤: |
| 14 | + |
| 15 | +1. 使用参数 $\theta$ 进行拟合,让数据集中的值与拟合算出的值的差值平方 $\sum_i(y^{(i)} − \theta^T x^{(i)} )^2$ 最小 (最小二乘法的思想); |
| 16 | +2. 输出 $\theta^T x$ 。 |
| 17 | + |
| 18 | +相应地,在 LWR 局部加权线性回归方法中,步骤如下: |
| 19 | + |
| 20 | +1. 使用参数 $\theta$ 进行拟合,让加权距离 $\sum_i w^{(i)}(y^{(i)} − \theta^T x^{(i)} )^2$ 最小; |
| 21 | +2. 输出 $\theta^T x$。 |
| 22 | + |
| 23 | + |
| 24 | +上面式子中的 $w^{(i)}$ 是非负的权值。直观点说就是,如果对应某个$i$ 的权值 $w^{(i)}$ 特别大,那么在选择拟合参数 $\theta$ 的时候,就要尽量让这一点的 $(y^{(i)} − \theta^T x^{(i)} )^2$ 最小。而如果权值$w^{(i)}$ 特别小,那么这一点对应的$(y^{(i)} − \theta^T x^{(i)} )^2$ 就基本在拟合过程中忽略掉了。 |
| 25 | + |
| 26 | +对于权值的选取可以使用下面这个比较标准的公式: |
| 27 | + |
| 28 | +$$ |
| 29 | +w^{(i)} = \exp(- \frac {(x^{(i)}-x)^2}{2\tau^2}) |
| 30 | +$$ |
| 31 | + |
| 32 | +>[!note] |
| 33 | +> |
| 34 | +>如果 $x$ 是有值的向量,那就要对上面的式子进行泛化,得到的是$w^{(i)} = \exp(− \frac {(x^{(i)}-x)^T(x^{(i)}-x)}{2\tau^2})$,或者:$w^{(i)} = \exp(− \frac {(x^{(i)}-x)^T\Sigma ^{-1}(x^{(i)}-x)}{2})$。 |
| 35 | +
|
| 36 | + |
| 37 | +要注意的是,权值是依赖每个特定的点 $x$ 的,而这些点正是我们要去进行预测评估的点。此外,如果 $|x^{(i)} − x|$ 非常小,那么权值 $w^{(i)} $ 就接近 $1$;反之如果 $|x^{(i)} − x|$ 非常大,那么权值 $w^{(i)} $ 就变小。所以可以看出, $\theta$ 的选择过程中,查询点 $x$ 附近的训练样本有更高得多的权值。(还要注意,虽然权值方程的形式跟高斯分布的概率密度函数比较接近,但权值和高斯分布并没有什么直接联系,权值有可能不是随机变量,不呈现正态分布或者其他形式分布。)训练样本的权值随 $x^{(i)}$ 与 $x$ 之间的距离增大而下降,参数$\tau$ 控制了下降的速度;$\tau$ 也叫做**带宽参数**。 |
| 38 | + |
| 39 | +局部加权线性回归是咱们接触的第一个**非参数** 算法。而更早之前咱们看到的无权重的线性回归算法就是一种**参数** 学习算法,因为有固定的有限个数的参数(也就是 $\theta_i$ ),这些参数用来拟合数据。我们对 $\theta_i$ 进行了拟合之后,就把它们存了起来,也就不需要再保留训练数据样本来进行更进一步的预测了。与之相反,如果用局部加权线性回归算法,我们就必须一直保留着整个训练集。这里的非参数算法中的 非参数 “non-parametric” 大约是指:为了呈现出假设 $h$ 随着数据集规模的增长而线性增长,我们需要以一定顺序保存一些数据的规模。(The term “non-parametric” (roughly) refers to the fact that the amount of stuff we need to keep in order to represent the hypothesis h grows linearly with the size of the training set. ) |
| 40 | + |
| 41 | +## LWR 的解析解 |
| 42 | + |
| 43 | +首先将损失函数写为矩阵形式: |
| 44 | +$$ |
| 45 | +\begin{align} |
| 46 | +J(\theta) &= \frac{1}{2} \sum_{i = 1}^{n} \omega^{(i)} (y^{(i)} - \theta^{\text T} x^{(i)})^2 \\ |
| 47 | +&= \frac{1}{2} (X \theta - \vec y)^{\text T} W (X \theta - \vec y), |
| 48 | +\end{align} |
| 49 | +$$ |
| 50 | +其中 |
| 51 | +$$ |
| 52 | +W = \begin{bmatrix} |
| 53 | +\omega^{(1)} \\ |
| 54 | +& \omega^{(2)} \\ |
| 55 | +& & \ddots \\ |
| 56 | +& & & \omega^{(n)} \\ |
| 57 | +\end{bmatrix}. |
| 58 | +$$ |
| 59 | +欲使损失函数最小,需对 $\theta$ 求导: |
| 60 | +$$ |
| 61 | +\begin{align} |
| 62 | +\nabla_{\theta} J(\theta) &= \frac{1}{2} \nabla_{\theta} (X \theta - \vec y)^{\text T} W (X \theta - \vec y) \\ |
| 63 | +&= \frac{1}{2} \nabla_{\theta} (\theta^{\text T} X^{\text T} - \vec y^{\text T})(WX\theta - W \vec y) \\ |
| 64 | +&= \frac{1}{2} \nabla_{\theta} (\theta^{\text T} (X^{\text T} W X) \theta - \theta^{\text T} (X^{\text T} W \vec y) - (\vec y^{\text T} W X) \theta - \vec y^{\text T} W \vec y) \\ |
| 65 | +&= \frac{1}{2} \nabla_{\theta} (\theta^{\text T} (X^{\text T} W X) \theta - \theta^{\text T} (X^{\text T} W \vec y) - (X^{\text T} W^{\text T} \vec y)^{\text T} \theta) \\ |
| 66 | +&= \frac{1}{2} \nabla_{\theta} (\theta^{\text T} (X^{\text T} W X) \theta - \theta^{\text T} (X^{\text T} W \vec y) - (X^{\text T} W \vec y)^{\text T} \theta) \\ |
| 67 | +&= \frac{1}{2} \nabla_{\theta} (\theta^{\text T} (X^{\text T} W X) \theta - 2\theta^{\text T} (X^{\text T} W \vec y)) \\ |
| 68 | +&= \frac{1}{2}(2 X^{\text T} W X \theta - 2 X^{\text T} W \vec y) \\ |
| 69 | +&= X^{\text T} WX \theta - X^{\text T} W \vec y. |
| 70 | +\end{align} |
| 71 | +$$ |
| 72 | +第五个等号利用了 $W^{\text T} = W$,第六个等号利用了向量内积的对称性,第七个等号利用了二次型求导和内积求导的相关结论。 |
| 73 | + |
| 74 | +故有 |
| 75 | +$$ |
| 76 | +\theta = (X^{\text T} WX)^{-1} X^{\text T} W \vec y. |
| 77 | +$$ |
0 commit comments