|
44 | 44 | "id": "ckzz5Hus-hJB" |
45 | 45 | }, |
46 | 46 | "source": [ |
47 | | - "# Part 1: Introduction to CAPSA" |
48 | | - ] |
49 | | - }, |
50 | | - { |
51 | | - "cell_type": "markdown", |
52 | | - "metadata": { |
53 | | - "id": "gTpt_Hj5j-FZ" |
54 | | - }, |
55 | | - "source": [ |
56 | | - "As we saw in lecture 6, it is critical to be able to estimate bias and uncertainty robustly: we need benchmarks that uniformly measure how uncertain a given model is, and we need principled ways of measuring bias and uncertainty. To that end, in this lab, we'll utilize [CAPSA](https://github.com/themis-ai/capsa), a risk-estimation wrapping library developed by [Themis AI](https://themisai.io/). CAPSA supports the estimation of three different types of *risk*, defined as measures of how trustworthy our model is. These are:\n", |
57 | | - "1. Representation bias: using a histogram estimation approach, CAPSA calculates how likely combinations of features are to appear in a given dataset. Often, certain combinations of features are severely underrepresented in datasets, which means models learn them less well. Since evaluation metrics are often also biased in the same manner, these biases are not caught through traditional validation pipelines.\n", |
58 | | - "2. Aleatoric uncertainty: we can estimate the uncertainty in *data* by learning a layer that predicts a standard deviation for every input. This is useful to determine when sensors have noise, classes in datasets have low separations, and generally when very similar inputs lead to drastically different outputs.\n", |
59 | | - "3. Epistemic uncertainty: also known as predictive or model uncertainty, epistemic uncertainty captures the areas of our underlying data distribution that the model has not yet learned. Areas of high epistemic uncertainty can be due to out of distribution (OOD) samples or data that is harder to learn.\n" |
| 47 | + "# Laboratory 3: Debiasing, Uncertainty, and Robustness\n", |
| 48 | + "\n", |
| 49 | + "# Part 1: Introduction to Capsa\n", |
| 50 | + "\n", |
| 51 | + "In this lab, we'll explore different ways to make deep learning models more **robust** and **trustworthy**.\n", |
| 52 | + "\n", |
| 53 | + "To achieve this it is critical to be able to identify and diagnose issues of bias and uncertainty in deep learning models, as we explored in the Facial Detection Lab 2. We need benchmarks that uniformly measure how uncertain a given model is, and we need principled ways of measuring bias and uncertainty. To that end, in this lab, we'll utilize [CAPSA](https://github.com/themis-ai/capsa), a risk-estimation wrapping library developed by [Themis AI](https://themisai.io/). CAPSA supports the estimation of three different types of ***risk***, defined as measures of how robust and trustworthy our model is. These are:\n", |
| 54 | + "1. **Representation bias**: reflects how likely combinations of features are to appear in a given dataset. Often, certain combinations of features are severely under-represented in datasets, which means models learn them less well and can thus lead to unwanted bias.\n", |
| 55 | + "2. **Data uncertainty**: reflects noise in the data, for example when sensors have noisy measurements, classes in datasets have low separations, and generally when very similar inputs lead to drastically different outputs. Also known as *aleatoric* uncertainty. \n", |
| 56 | + "3. **Model uncertainty**: captures the areas of our underlying data distribution that the model has not yet learned or has difficulty learning. Areas of high model uncertainty can be due to out-of-distribution (OOD) samples or data that is harder to learn. Also known as *epistemic* uncertainty." |
60 | 57 | ] |
61 | 58 | }, |
62 | 59 | { |
|
65 | 62 | "id": "o02MyoDrnNqP" |
66 | 63 | }, |
67 | 64 | "source": [ |
68 | | - "The core ideology behind CAPSA is that models can be *wrapped* in a way that makes them *risk-aware*. \n", |
| 65 | + "## CAPSA overview\n", |
| 66 | + "\n", |
| 67 | + "This lab introduces `CAPSA` and its functionalities, to next build automated tools that use `CAPSA` to mitigate the underlying issues of bias and uncertainty.\n", |
| 68 | + "\n", |
| 69 | + "The core idea behind `CAPSA` is that any deep learning model of interest can be ***wrapped*** -- just like wrapping a gift -- to be made ***aware of its own risks***. Risk is captured in representation bias, data uncertainty, and model uncertainty.\n", |
69 | 70 | "\n", |
70 | 71 | "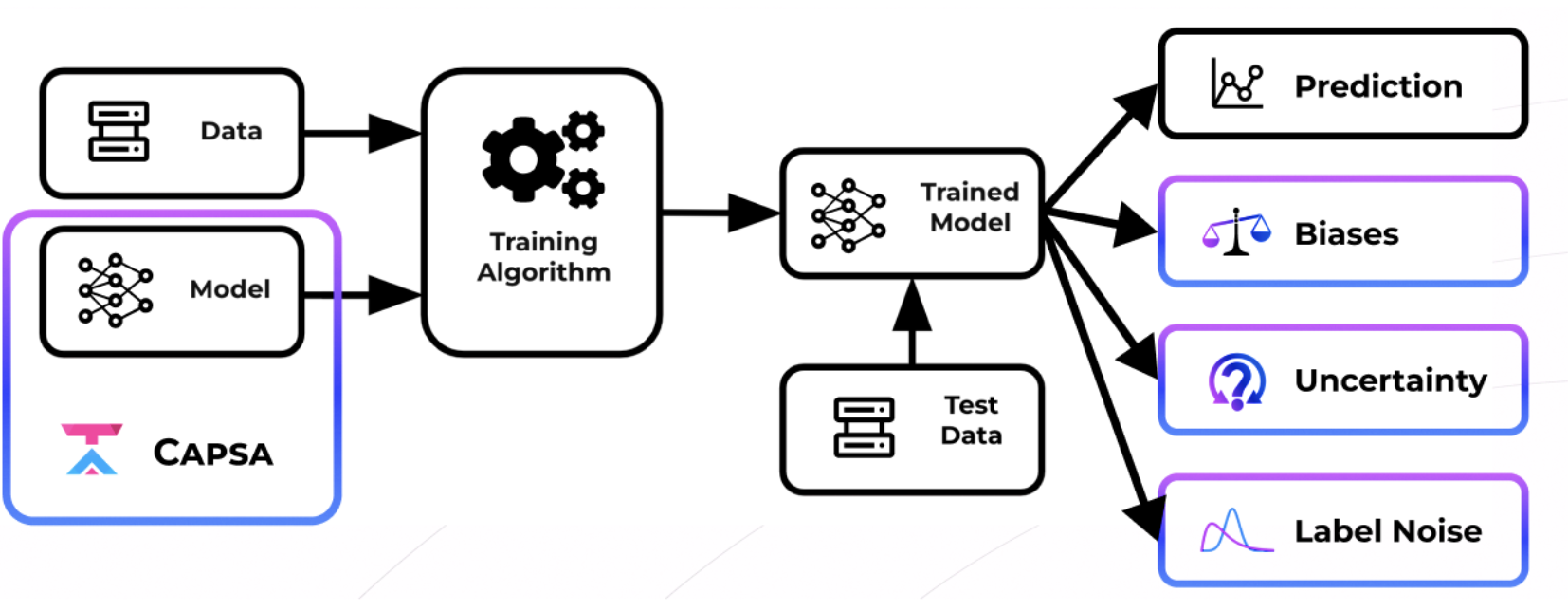\n", |
71 | 72 | "\n", |
72 | | - "This means that CAPSA augments or modifies the user's original model minimally to create a risk-aware variant while preserving the model's underlying structure and training pipeline. CAPSA is a one-line addition to any training workflow in Tensorflow. In this part of the lab, we'll apply CAPSA's risk estimation methods to a toy regression task to further explore the notions of bias and uncertainty. " |
| 73 | + "This means that `CAPSA` takes the user's original model as input, and modifies it minimally to create a risk-aware variant while preserving the model's underlying structure and training pipeline. `CAPSA` is a one-line addition to any training workflow in TensorFlow. In this part of the lab, we'll apply `CAPSA`'s risk estimation methods to a simple regression problem to further explore the notions of bias and uncertainty. " |
73 | 74 | ] |
74 | 75 | }, |
75 | 76 | { |
|
78 | 79 | "id": "hF0uSqk-nwmA" |
79 | 80 | }, |
80 | 81 | "source": [ |
81 | | - "Let's first install necessary dependencies:" |
| 82 | + "Let's get started by installing the necessary dependencies:" |
82 | 83 | ] |
83 | 84 | }, |
84 | 85 | { |
|
112 | 113 | } |
113 | 114 | ], |
114 | 115 | "source": [ |
| 116 | + "# Import Tensorflow 2.0\n", |
| 117 | + "%tensorflow_version 2.x\n", |
115 | 118 | "import tensorflow as tf\n", |
116 | | - "import numpy as np\n", |
117 | | - "import matplotlib.pyplot as plt\n", |
118 | | - "!pip install capsa\n", |
119 | 119 | "\n", |
120 | | - "from capsa import *\n", |
| 120 | + "import IPython\n", |
| 121 | + "import functools\n", |
| 122 | + "import matplotlib.pyplot as plt\n", |
| 123 | + "import numpy as np\n", |
| 124 | + "from tqdm import tqdm\n", |
121 | 125 | "from helper import gen_data_regression\n", |
122 | 126 | "\n", |
| 127 | + "# Download and import the MIT Introduction to Deep Learning package\n", |
123 | 128 | "!pip install mitdeeplearning\n", |
124 | 129 | "import mitdeeplearning as mdl\n", |
125 | | - "import tqdm" |
| 130 | + "\n", |
| 131 | + "# Download and import CAPSA\n", |
| 132 | + "!pip install capsa\n", |
| 133 | + "from capsa import *" |
126 | 134 | ] |
127 | 135 | }, |
128 | 136 | { |
|
131 | 139 | "id": "xzEcxjKHn8gc" |
132 | 140 | }, |
133 | 141 | "source": [ |
134 | | - "### 1.1 Datasets \n", |
135 | | - "Next, let's construct a dataset that we'll analyze. As shown in lecture, we'll look at the curve `y = x^3` with epistemic and aleatoric noise added to certain parts of the dataset. The blue points below are the test data: note that there are regions where we have no train data but we have test data! Do you expect these areas to have higher or lower uncertainty? What type of uncertainty?" |
| 142 | + "## 1.1 Dataset\n", |
| 143 | + "\n", |
| 144 | + "We will build understanding of bias and uncertainty by training a neural network for a simple 2D regression task: modeling the function $y = x^3$. We will use `CAPSA` to analyze this dataset and the performance of the model. Noise and missing-ness will be injected into the dataset.\n", |
| 145 | + "\n", |
| 146 | + "Let's generate the dataset and visualize it:" |
136 | 147 | ] |
137 | 148 | }, |
138 | 149 | { |
|
178 | 189 | "plt.show()" |
179 | 190 | ] |
180 | 191 | }, |
| 192 | + { |
| 193 | + "cell_type": "markdown", |
| 194 | + "source": [ |
| 195 | + "In the plot above, the orange points are the training data, which will be used as inputs to train the neural network model. The blue points are the test data, which will be used to evaluate the performance of the model. Write short (~1 sentence) answers to the questions below to complete the `TODO`s:\n", |
| 196 | + "\n", |
| 197 | + "#### **TODO: Inspecting the 2D regression dataset**\n", |
| 198 | + "1. What are your observations about where the train data and test data lie relative to each other?\n", |
| 199 | + "2. What, if any, areas do you expect to have high/low aleatoric (data) uncertainty?\n", |
| 200 | + "3. What, if any, areas do you expect to have high/low epistemic (model) uncertainty?" |
| 201 | + ], |
| 202 | + "metadata": { |
| 203 | + "id": "Fz3UxT8vuN95" |
| 204 | + } |
| 205 | + }, |
181 | 206 | { |
182 | 207 | "cell_type": "markdown", |
183 | 208 | "metadata": { |
|
313 | 338 | }, |
314 | 339 | "source": [ |
315 | 340 | "### 1.3 Bias Identification\n", |
316 | | - "Now that we've seen what the predictions from this model look like, let's see what the uncertainty and bias look like! To do this, we'll wrap a model first with a `HistogramWrapper`. For low-dimensional data, the HistogramWrapper bins the input directly into discrete categories and measures the density. " |
| 341 | + "Now that we've seen what the predictions from this model look like, let's see what the uncertainty and bias look like! To do this, we'll wrap a model first with a `HistogramWrapper`. For low-dimensional data, the HistogramWrapper bins the input directly into discrete categories and measures the density. \n", |
| 342 | + "\n", |
| 343 | + "--- FROM INTRO ---\n", |
| 344 | + "\n", |
| 345 | + "using a histogram estimation approach, CAPSA calculates how likely combinations of features are to appear in a given dataset. \n", |
| 346 | + "\n", |
| 347 | + " Since evaluation metrics are often also biased in the same manner, these biases are not caught through traditional validation pipelines." |
317 | 348 | ] |
318 | 349 | }, |
319 | 350 | { |
|
497 | 528 | }, |
498 | 529 | "source": [ |
499 | 530 | "## 1.3 Aleatoric Estimation\n", |
500 | | - "Now, let's do the same thing but for aleatoric estimation! The method we use here is Mean and Variance Estimation (MVE) since we're trying to estimate both mean and variance for every input. As presented in lecture 5, we measure the accuracy of these predictions negative likelihood loss in addition to mean squared error. However, capsa *automatically* does this for us, so we only have to specify the loss function that we want to use for evaluating the predictions, not the uncertainty." |
| 531 | + "Now, let's do the same thing but for aleatoric estimation! The method we use here is Mean and Variance Estimation (MVE) since we're trying to estimate both mean and variance for every input. As presented in lecture 5, we measure the accuracy of these predictions negative likelihood loss in addition to mean squared error. However, capsa *automatically* does this for us, so we only have to specify the loss function that we want to use for evaluating the predictions, not the uncertainty.\n", |
| 532 | + "\n", |
| 533 | + "we can estimate data uncertainty by learning a layer that predicts a standard deviation for every input." |
501 | 534 | ] |
502 | 535 | }, |
503 | 536 | { |
|
825 | 858 | "\n", |
826 | 859 | "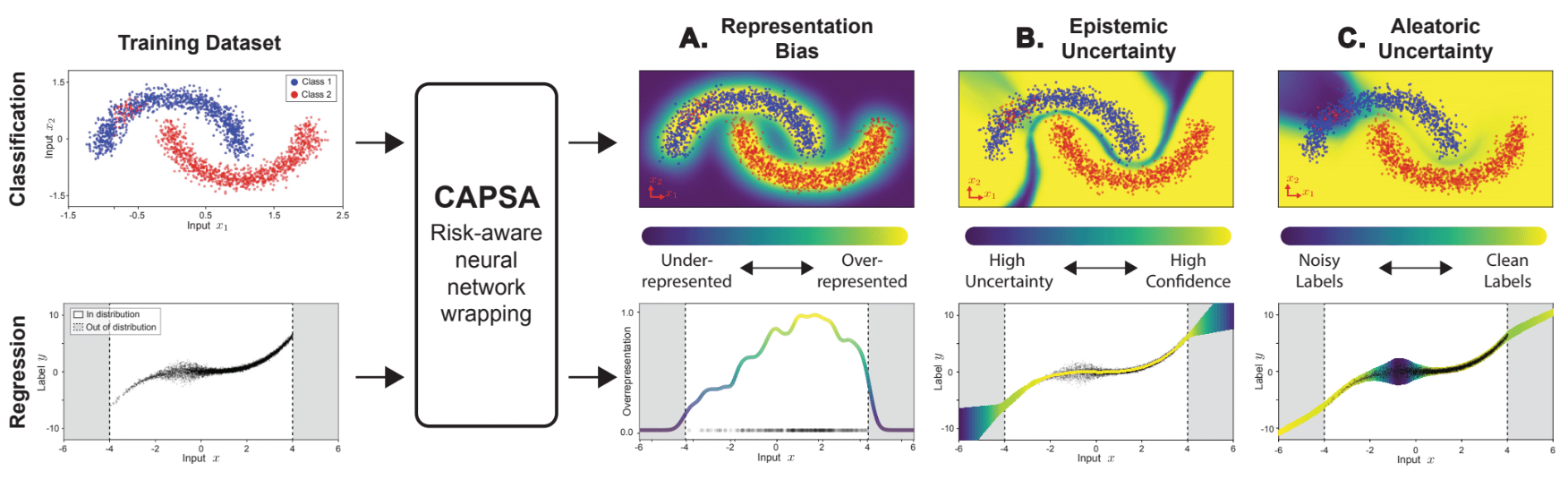" |
827 | 860 | ] |
828 | | - }, |
829 | | - { |
830 | | - "cell_type": "code", |
831 | | - "execution_count": null, |
832 | | - "metadata": { |
833 | | - "id": "bs4mAQ5c6cMY" |
834 | | - }, |
835 | | - "outputs": [], |
836 | | - "source": [] |
837 | 861 | } |
838 | 862 | ], |
839 | 863 | "metadata": { |
|
0 commit comments