Skip to content

Commit 468ba81

Browse files
HydrogenSulfateHydrogenSulfate
authored
[Example] add fundiff(turbulence_mass_transfer) (#1189)
* add fundiff(turbulence_mass_transfer) * fix docs
1 parent 931e5c5 commit 468ba81

File tree

9 files changed

+1744
-2
lines changed

9 files changed

+1744
-2
lines changed

‎docs/requirements.txt

Lines changed: 2 additions & 2 deletions
Original file line numberDiff line numberDiff line change
@@ -9,8 +9,8 @@ mkdocs-include-markdown-plugin
99
mkdocs-material
1010
mkdocs-material-extensions
1111
mkdocs-video
12-
mkdocstrings==0.27.0
13-
mkdocstrings-python
12+
mkdocstrings==0.29.0
13+
mkdocstrings-python==1.16.12
1414
numpy>=1.20.0,<2.0.0
1515
pyyaml
1616
scipy

‎docs/zh/examples/fundiff.md

Lines changed: 205 additions & 0 deletions
Original file line numberDiff line numberDiff line change
@@ -0,0 +1,205 @@
1+
# FunDiff
2+
3+
<!-- <a href="https://aistudio.baidu.com/projectdetail/7927786" class="md-button md-button--primary" style>AI Studio快速体验</a> -->
4+
5+
!!! warning
6+
7+
本文档仅复现了 Fundiff 论文中的 turbulence_mass_transfer 任务
8+
9+
!!! note
10+
11+
请先在 <https://drive.google.com/drive/folders/1GX5uG_3R-yfuP9nMIk0v7ChuEytYwYPW?usp=drive_link> 中下载 tmt.npy 数据集文件
12+
13+
=== "模型训练命令"
14+
15+
``` sh
16+
python main.py -cn fae.yaml
17+
18+
python main.py -cn diffusion.yaml FAE.pretrained_model_path=/your/fae/pretrained/model/path
19+
```
20+
21+
=== "模型评估命令"
22+
23+
``` sh
24+
python main.py -cn diffusion.yaml mode=eval EVAL.pretrained_model_path=https://paddle-org.bj.bcebos.com/paddlescience/models/fundiff/fundiff_turbulence_mass_transfer_dit_pretrained.pdparams
25+
```
26+
27+
<!-- === "模型导出命令"
28+
29+
暂无
30+
31+
=== "模型推理命令"
32+
33+
暂无 -->
34+
35+
| 预训练模型 | 指标 |
36+
|:--| :--|
37+
| [fundiff_turbulence_mass_transfer_dit_pretrained.pdparams](https://paddle-org.bj.bcebos.com/paddlescience/models/fundiff/fundiff_turbulence_mass_transfer_dit_pretrained.pdparams) | Mean relative p error: 0.0755<br>Max relative p error: 0.1976<br>Min relative p error: 0.0225<br>Std relative p error: 0.0389<br>Mean relative sdf error: 0.0841<br>Max relative sdf error: 0.2972<br>Min relative sdf error: 0.0205<br>Std relative sdf error: 0.0609 |
38+
39+
## 1. 背景简介
40+
41+
生成模型（尤其是扩散模型和流匹配）的最新进展在图像和视频等离散数据的合成方面取得了显著成功。然而，将这些模型应用于物理应用仍然具有挑战性，因为感兴趣的物理量是由复杂物理定律支配的连续函数。本文介绍了 $\textbf{FunDiff}$，这是一个用于函数空间生成模型的全新框架。FunDiff 将潜在扩散过程与函数自编码器架构相结合，以处理具有不同离散化程度的输入函数，生成可在任意位置求值的连续函数，并无缝地集成物理先验。这些先验通过架构约束或基于物理的损失函数来强制执行，从而确保生成的样本满足基本物理定律。作者从理论上建立了函数空间中密度估计的极小极大最优性保证，表明基于扩散的估计器在合适的正则条件下能够实现最佳收敛速度。结果中展示了 FunDiff 在流体动力学和固体力学等各种应用中的实际有效性。实证结果表明，作者的方法能够生成物理上一致的样本，与目标分布高度一致，并且对噪声数据和低分辨率数据表现出鲁棒性。
42+
43+
## 2. 问题定义
44+
45+
给定已知物理场 $u$ 和 $v$，求解物理场 $p$ 以及 $sdf$。
46+
47+
## 3. 问题求解
48+
49+
接下来开始讲解如何将问题一步一步地转化为 PaddleScience 代码，用深度学习的方法求解该问题。
50+
为了快速理解 PaddleScience，接下来仅对模型构建、方程构建、计算域构建等关键步骤进行阐述，而其余细节请参考 [API文档](../api/arch.md)。
51+
52+
### 3.1 训练 FAE
53+
54+
#### 3.1.1 FAE 模型构建
55+
56+
在 FuncDiff 模型中，FAE 模块采用了 Perceiver 的架构，其输入为物理场 $x$ 和查询坐标 $coords$，输出是某个物理场在查询坐标上的值 $u$，因此模型构建代码如下
57+
58+
``` yaml linenums="36"
59+
--8<--
60+
examples/fundiff/conf/fae.yaml:36:63
61+
--8<--
62+
```
63+
64+
``` py linenums="87"
65+
--8<--
66+
examples/fundiff/main.py:87:95
67+
--8<--
68+
```
69+
70+
#### 3.1.2 约束构建
71+
72+
FAE 使用 auto encoder decoder 的训练范式，因此标签即是输入 $u$
73+
74+
``` py linenums="97"
75+
--8<--
76+
examples/fundiff/main.py:97:148
77+
--8<--
78+
```
79+
80+
### 3.2 训练 DiT
81+
82+
#### 3.2.1 DiT 模型构建
83+
84+
DiT 的模型构建如下
85+
86+
``` yaml linenums="66"
87+
--8<--
88+
examples/fundiff/conf/diffusion.yaml:66:76
89+
--8<--
90+
```
91+
92+
``` py linenums="186"
93+
--8<--
94+
examples/fundiff/main.py:186:208
95+
--8<--
96+
```
97+
98+
#### 3.2.2 约束构建
99+
100+
在 FuncDiff 模型中，DiT 的训练使用 rectified flow 算法，其对应的数学公式如下：
101+
102+
$$
103+
\mathcal{L}(\theta) = \mathbb{E}_{\mathbf{z}, t, {\epsilon}} \left[ \left\| \hat{\mathbf{v}}_\theta(\mathbf{x}, t) - (\mathbf{z} - \mathbf{x}) \right\|^2 \right]
104+
$$
105+
106+
其对应的前向计算实现代码如下
107+
108+
``` py linenums="44"
109+
--8<--
110+
examples/fundiff/main.py:44:85
111+
--8<--
112+
```
113+
114+
整体约束构建如下
115+
116+
``` py linenums="210"
117+
--8<--
118+
examples/fundiff/main.py:210:262
119+
--8<--
120+
```
121+
122+
### 3.3 超参数设定
123+
124+
FAE 使用 100000 步训练步数，0.001 的初始学习率。
125+
126+
``` yaml linenums="65" title="fae.yaml"
127+
--8<--
128+
examples/fundiff/conf/fae.yaml:65:80
129+
--8<--
130+
```
131+
132+
DiT 使用 100000 步训练步数，0.001 的初始学习率。
133+
134+
``` yaml linenums="78" title="diffusion.yaml"
135+
--8<--
136+
examples/fundiff/conf/diffusion.yaml:78:92
137+
--8<--
138+
```
139+
140+
### 3.4 优化器构建
141+
142+
训练过程会调用优化器来更新模型参数，FAE 和 DiT 均选择较为常用的 `Adam` 优化器，并配合使用机器学习中常用的 ExponentialDecay 学习率调整策略。
143+
144+
``` yaml linenums="65" title="fae.yaml"
145+
--8<--
146+
examples/fundiff/conf/fae.yaml:65:80
147+
--8<--
148+
```
149+
150+
``` py linenums="159"
151+
--8<--
152+
examples/fundiff/main.py:159:172
153+
--8<--
154+
```
155+
156+
``` yaml linenums="78" title="diffusion.yaml"
157+
--8<--
158+
examples/fundiff/conf/diffusion.yaml:78:104
159+
--8<--
160+
```
161+
162+
``` py linenums="273" title="main.py"
163+
--8<--
164+
examples/fundiff/main.py:273:286
165+
--8<--
166+
```
167+
168+
### 3.5 模型训练
169+
170+
完成上述设置之后，只需要将上述实例化的对象按顺序传递给 `ppsci.solver.Solver`，然后启动训练即可。
171+
172+
``` py linenums="174"
173+
--8<--
174+
examples/fundiff/main.py:174:182
175+
--8<--
176+
```
177+
178+
``` py linenums="288"
179+
--8<--
180+
examples/fundiff/main.py:288:296
181+
--8<--
182+
```
183+
184+
## 4. 完整代码
185+
186+
``` py linenums="1" title="main.py"
187+
--8<--
188+
examples/fundiff/main.py
189+
--8<--
190+
```
191+
192+
## 5. 结果展示
193+
194+
在测试集上进行评估，并对部分结果进行展示
195+
196+
<figure markdown>
197+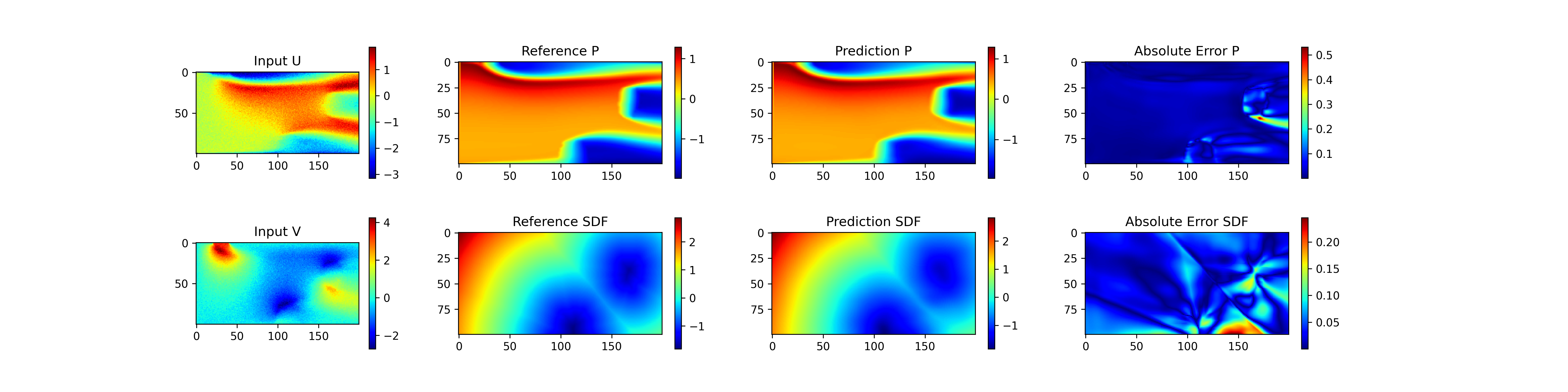
![result_of_sample_2.jpg](https://paddle-org.bj.bcebos.com/paddlescience/docs/fundiff/result_of_sample_2.png){ loading=lazy }
198+
</figure>
199+
200+
可以看到对于函数$p(x, coord | u,v)$ 和$sdf(x, coord | u,v)$，模型的预测结果和参考结果基本一致。
201+
202+
## 6. 参考资料
203+
204+
- [FunDiff: Diffusion Models over Function Spaces for Physics-Informed Generative Modeling](https://arxiv.org/abs/2506.07902v1)
205+
- [fundiff github](https://github.com/sifanexisted/fundiff/tree/main)

‎examples/fundiff/conf/diffusion.yaml

Lines changed: 130 additions & 0 deletions
Original file line numberDiff line numberDiff line change
@@ -0,0 +1,130 @@
1+
defaults:
2+
- ppsci_default
3+
- TRAIN: train_default
4+
- TRAIN/ema: ema_default
5+
- TRAIN/swa: swa_default
6+
- EVAL: eval_default
7+
- INFER: infer_default
8+
- hydra/job/config/override_dirname/exclude_keys: exclude_keys_default
9+
- _self_
10+
11+
hydra:
12+
run:
13+
# dynamic output directory according to running time and override name
14+
dir: outputs_dit/${now:%Y-%m-%d}/${now:%H-%M-%S}_${mode}/${hydra.job.override_dirname}
15+
job:
16+
name: ${mode} # name of logfile
17+
chdir: false # keep current working directory unchanged
18+
callbacks:
19+
init_callback:
20+
_target_: ppsci.utils.callbacks.InitCallback
21+
sweep:
22+
# output directory for multirun
23+
dir: ${hydra.run.dir}
24+
subdir: ./
25+
26+
# general settings
27+
mode: train # running mode: train/eval
28+
stage: dit # fae, dit
29+
seed: 42
30+
output_dir: ${hydra:run.dir}
31+
log_freq: 100
32+
33+
DATA_PATH: ./data/turbulence_mass_transfer/tmt.npy
34+
num_train: 900
35+
36+
# model settings
37+
FAE:
38+
input_keys: [coords, x]
39+
output_keys: [u]
40+
# x_dim: [2, 200, 100, 1]
41+
# c_dim: [2, 256, 512]
42+
# t_dim: [2]
43+
encoder:
44+
in_dim: 1
45+
patch_size: [10, 5]
46+
emb_dim: 256
47+
num_latents: 256
48+
grid_size: [200, 100]
49+
depth: 8
50+
num_heads: 8
51+
mlp_ratio: 2
52+
layer_norm_eps: 1e-05
53+
decoder:
54+
in_dim: 2
55+
period: null
56+
fourier_freq: 1.0
57+
dec_emb_dim: 256
58+
dec_depth: 4
59+
dec_num_heads: 8
60+
mlp_ratio: 2
61+
num_mlp_layers: 2
62+
out_dim: 1
63+
layer_norm_eps: 1e-05
64+
pretrained_model_path: null
65+
66+
DIT:
67+
# input_keys: [u, v, p, sdf]
68+
# output_keys: [v_t_err]
69+
in_dim: 512
70+
depth: 8
71+
emb_dim: 512
72+
mlp_ratio: 2
73+
num_heads: 16
74+
seq_len: 256
75+
out_dim: 512
76+
with_condition: true
77+
78+
# training settings
79+
TRAIN:
80+
steps: 100000
81+
epochs: 10000
82+
iters_per_epoch: -1
83+
solution: [1, 2, 4]
84+
save_freq: 0
85+
eval_during_train: false
86+
eval_freq: 10
87+
optim: adam
88+
beta1: 0.9
89+
beta2: 0.999
90+
eps: 1e-8
91+
weight_decay: 1e-5
92+
clip_norm: 1.0
93+
94+
lr_scheduler:
95+
# epochs: ${TRAIN.epochs}
96+
learning_rate: 0.001
97+
gamma: 0.9
98+
decay_steps: 5000
99+
by_epoch: false
100+
warmup_epoch: 2000
101+
102+
batch_size: 64
103+
pretrained_model_path: null
104+
checkpoint_path: null
105+
106+
# evaluation settings
107+
EVAL:
108+
pretrained_model_path: null
109+
eval_with_no_grad: true
110+
batch_size: 8
111+
num_steps: 100
112+
use_conditioning: true
113+
114+
# inference settings
115+
INFER:
116+
pretrained_model_path: null
117+
export_path: ./inference/fae
118+
pdmodel_path: ${INFER.export_path}.pdmodel
119+
pdiparams_path: ${INFER.export_path}.pdiparams
120+
onnx_path: ${INFER.export_path}.onnx
121+
device: gpu
122+
engine: native
123+
precision: fp32
124+
ir_optim: true
125+
min_subgraph_size: 5
126+
gpu_mem: 2000
127+
gpu_id: 0
128+
max_batch_size: 1024
129+
num_cpu_threads: 10
130+
batch_size: 1024

0 commit comments

Comments
 (0)