|
| 1 | +# NTopo: Mesh-free Topology Optimization using Implicit Neural Representations |
| 2 | + |
| 3 | +=== "模型训练命令" |
| 4 | + |
| 5 | + ``` sh |
| 6 | + python ntopo.py |
| 7 | + ``` |
| 8 | + |
| 9 | +=== "模型评估命令" |
| 10 | + |
| 11 | + ``` sh |
| 12 | + python ntopo.py mode=eval PROBLEM=Beam2D EVAL.pretrained_model_path_density=https://paddle-org.bj.bcebos.com/paddlescience/models/ntopo/beam2d_pretrained.pdparams |
| 13 | + python ntopo.py mode=eval PROBLEM=Bridge2D EVAL.pretrained_model_path_density=https://paddle-org.bj.bcebos.com/paddlescience/models/ntopo/bridge2d_pretrained.pdparams |
| 14 | + python ntopo.py mode=eval PROBLEM=Distributed2D EVAL.pretrained_model_path_density=https://paddle-org.bj.bcebos.com/paddlescience/models/ntopo/distributed2d_pretrained.pdparams |
| 15 | + python ntopo.py mode=eval PROBLEM=LongBeam2D EVAL.pretrained_model_path_density=https://paddle-org.bj.bcebos.com/paddlescience/models/ntopo/longbeam2d_pretrained.pdparams |
| 16 | + python ntopo.py mode=eval PROBLEM=LShape2D EVAL.pretrained_model_path_density=https://paddle-org.bj.bcebos.com/paddlescience/models/ntopo/lshape2d_pretrained.pdparams |
| 17 | + python ntopo.py mode=eval PROBLEM=Triangle2D EVAL.pretrained_model_path_density=https://paddle-org.bj.bcebos.com/paddlescience/models/ntopo/triangle2d_pretrained.pdparams |
| 18 | + python ntopo.py mode=eval PROBLEM=TriangleVariants2D EVAL.pretrained_model_path_density=https://paddle-org.bj.bcebos.com/paddlescience/models/ntopo/trianglevariants2d_pretrained.pdparams |
| 19 | + python ntopo.py --config-name ntopo.yaml mode=eval PROBLEM=Beam3D EVAL.pretrained_model_path_density=https://paddle-org.bj.bcebos.com/paddlescience/models/ntopo/beam3d_pretrained.pdparams |
| 20 | + python ntopo.py --config-name ntopo.yaml mode=eval PROBLEM=Bridge3D EVAL.pretrained_model_path_density=https://paddle-org.bj.bcebos.com/paddlescience/models/ntopo/bridge3d_pretrained.pdparams |
| 21 | + ``` |
| 22 | + |
| 23 | +*注:由于该案例训练方法较为特殊,没有参考指标,训练完成后直接生成可视化结果,以判断训练效果。* |
| 24 | + |
| 25 | +## 1. 背景简介 |
| 26 | + |
| 27 | +在拓扑优化问题中有一种常见的方法 SIMP(Solid Isotropic Material with Penalization),它是一种基于密度法的拓扑优化方法,通过连续设计变量(材料密度)描述设计域内各点的材料分布,最终逼近理想的“0-1”二元分布(材料存在或不存在)。其核心目标是优化材料布局,在满足约束条件(如体积、刚度)下实现特定性能目标(如最小柔顺度)。 |
| 28 | + |
| 29 | +在传统的数值计算中,SIMP 将设计域离散为有限元网格,每个单元分配连续密度变量 $\rho \in [0,1]$,然后引入幂律插值函数和惩罚因子,通过数学公式将中间密度值向0或1方向惩罚,抑制灰度区域,例如,弹性模量插值公式为:$E(\rho) = \rho^p E_1$ |
| 30 | + |
| 31 | +该案例提出了一种基于隐式神经表示的新型机器学习方法,用于解决拓扑优化这一高难度逆问题。传统方法依赖网格化处理,而该案例通过 MLP 无网格化地参数化密度场和位移场,利用神经网络的连续可微特性生成高细节解。实验表明,该方法在结构顺应性目标优化中表现优异,并能通过自监督学习探索拓扑优化问题的连续解空间,克服了传统方法在高维参数空间和非线性目标函数中的局限性。核心创新在于将神经表示与无网格优化结合,为复杂逆问题提供了高效且灵活的解决方案。 |
| 32 | + |
| 33 | +## 2. 问题定义 |
| 34 | + |
| 35 | +拓扑优化(TO)的目标是在给定的边界条件、作用力和目标材料体积比下,找到使结构最刚硬的材料分布。这一问题可以形式化为一个带约束的双层最小化问题: |
| 36 | + |
| 37 | +$$ |
| 38 | +\begin{cases} |
| 39 | + \min_{\rho}L_{comp}(\rho)=\int_{\Omega}e(\rho,u(\rho),\omega)d\omega \\ |
| 40 | + s.t. \quad u(\rho)=\arg\min_{u} L_{sim}(u,\rho) \\ |
| 41 | + \rho(\omega) \in {0, 1}, \quad \frac{1}{|\Omega|} \int_{\Omega} \rho d\omega = \hat{V} \\ |
| 42 | +\end{cases} |
| 43 | +$$ |
| 44 | + |
| 45 | +其中 $L_{comp}(\rho)$ 是顺应性损失函数; $e(\rho, u(\rho), \omega)$ 是点顺应性,与内部能量成正比; $u(\rho)$ 是位移场,满足力平衡条件,通过最小化模拟损失 $L_{sim}(u, \rho)$ 得到; $\rho(\omega)$ 是材料密度场,理论上取值为 $0$ 或 $1$(表示有无材料),但在实际优化中允许连续值,并鼓励收敛到二进制解; $\Omega$ 是设计域,$\omega$ 是空间坐标; $\hat{V}$ 是目标材料体积比。 |
| 46 | + |
| 47 | +## 3. 问题求解 |
| 48 | + |
| 49 | +接下来开始讲解如何将问题一步一步地转化为 PaddleScience 代码,用深度学习的方法求解该问题。 |
| 50 | +为了快速理解 PaddleScience,接下来仅对模型构建、方程构建、计算域构建等关键步骤进行阐述,而其余细节请参考 [API文档](../api/arch.md)。 |
| 51 | + |
| 52 | +### 3.1 模型构建 |
| 53 | + |
| 54 | +<figure markdown> |
| 55 | + 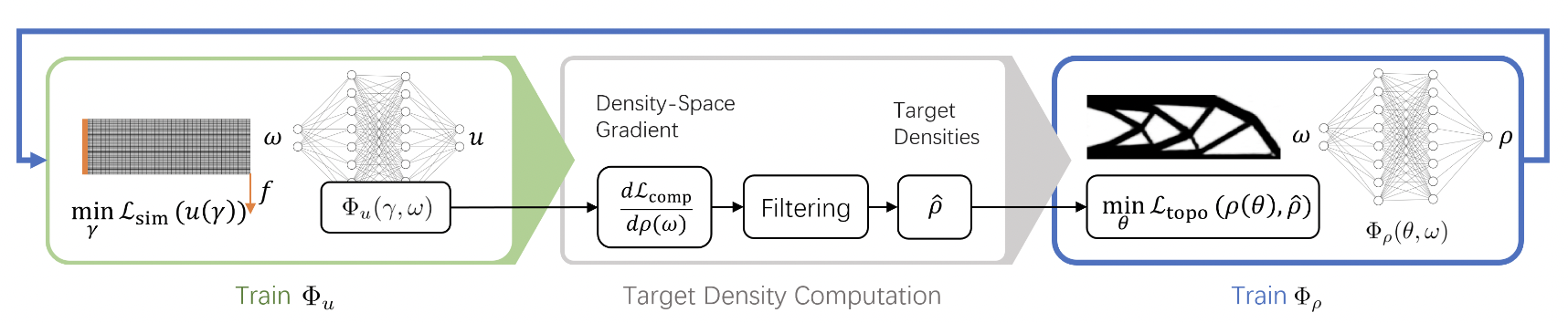{ loading=lazy style="margin:0 auto"} |
| 56 | + <figcaption> 训练整体流程 </figcaption> |
| 57 | +</figure> |
| 58 | + |
| 59 | +上图为训练整体流程,通过交替训练位移网络和密度网络这两个神经网络,分别将空间坐标 $ω$ 映射到平衡位移 $u$ 和最优密度 $\rho$ 来计算最优材料分布。在每次迭代中,首先通过最小化系统的总势能来更新位移网络,随后进行灵敏度分析以计算密度空间梯度,并通过灵敏度滤波生成目标密度场 $\hat{\rho}$。最后,通过最小化基于当前密度与目标密度均方误差的凸优化目标函数来更新密度网络。 |
| 60 | + |
| 61 | +位移网络和密度网络都是使用 SIREN 激活函数的 MLP 网络,具体代码请参考 [完整代码](#4) 中 model.py 文件。 |
| 62 | + |
| 63 | +### 3.2 参数和超参数设定 |
| 64 | + |
| 65 | +我们需要指定问题相关的参数,如要优化的问题的名称(几何类型)、材料参数、优化目标(体积百分比)等: |
| 66 | + |
| 67 | +``` yaml linenums="34" |
| 68 | +--8<-- |
| 69 | +examples/ntopo/conf/ntopo_2d.yaml:34:50 |
| 70 | +--8<-- |
| 71 | +``` |
| 72 | + |
| 73 | +另外需要在配置文件中指定训练轮数、`batch_size` 等其他训练所需参数,注意这里两个网络单独的 `epochs` 参数需要设置为 $1$: |
| 74 | + |
| 75 | +``` yaml linenums="69" |
| 76 | +--8<-- |
| 77 | +examples/ntopo/conf/ntopo_2d.yaml:69:101 |
| 78 | +--8<-- |
| 79 | +``` |
| 80 | + |
| 81 | +特别需要注意的是该案例中使用了一些技巧,如使用移动平方误差(MMSE)、基于多批次的最佳标准方法(OC)、滤波,它们相关的参数以及训练的 `iters_per_epoch` 需要谨慎设定,并非某个参数越大越好,不同的参数设置可能导向不同的优化结果。 |
| 82 | + |
| 83 | +### 3.3 优化器构建 |
| 84 | + |
| 85 | +训练过程会调用优化器来更新模型参数,此处选择 `Adam` 优化器。 |
| 86 | + |
| 87 | +``` py linenums="44" |
| 88 | +--8<-- |
| 89 | +examples/ntopo/ntopo.py:44:50 |
| 90 | +--8<-- |
| 91 | +``` |
| 92 | + |
| 93 | +### 3.4 方程构建 |
| 94 | + |
| 95 | +如 [问题定义](#2) 中所述,模型训练过程中需要使用弹性模量插值公式等公式,因此需要定义方程,具体代码请参考 [完整代码](#4) 中 equation.py 文件。 |
| 96 | + |
| 97 | +### 3.5 问题构建(包含 loss) |
| 98 | + |
| 99 | +本问题的计算域为初始几何结构,本案例中提供了部分 2D 及 3D 问题的类,其中包含了对计算域、边界条件、受力情况等多种参数和条件的定义,具体代码请参考 [完整代码](#4) 中 problems.py 文件。 |
| 100 | + |
| 101 | +其中值得注意的是,该案例中使用了一些技巧,如基于多批次的最佳标准方法(OC),这种方法需要一个批次的输入、输出数据,然后以某种方式计算得到该批次的 loss。 |
| 102 | + |
| 103 | +### 3.6 约束构建 |
| 104 | + |
| 105 | +本案例代码中存在 1 种内部点约束和 1 种监督约束(但实际上 loss 计算时没有用到标签,由于调用了 API, 这里按照约束的方式介绍)。 |
| 106 | + |
| 107 | +#### 3.6.1 内部点约束 |
| 108 | + |
| 109 | +几何内部的点存在约束 `InteriorConstraint`: |
| 110 | + |
| 111 | +``` py linenums="74" |
| 112 | +--8<-- |
| 113 | +examples/ntopo/ntopo.py:74:86 |
| 114 | +--8<-- |
| 115 | +``` |
| 116 | + |
| 117 | +`InteriorConstraint` 的第一个参数是方程(组)表达式,用于描述如何计算约束目标,此处填入在 [3.4 方程构建](#34) 章节中实例化好的 `problem.equation["EEquation"].equations`; |
| 118 | + |
| 119 | +第二个参数是约束变量的目标值,在本问题按照中希望与方程相关的 $E$ 值 `E_xyz` 或 `E_xy` 被优化至 0; |
| 120 | + |
| 121 | +第三个参数是约束方程作用的计算域,此处填入在 [3.5 问题构建](#35) 章节实例化好的相应问题的计算域 `problem.geom["geo"]` ; |
| 122 | + |
| 123 | +第四个参数是在计算域上的采样配置。 |
| 124 | + |
| 125 | +第五个参数是损失函数,此处通过 `ppsci.loss.FunctionalLoss` 传入自定义损失函数 `problem.disp_loss_func`; |
| 126 | + |
| 127 | +第六个是约束条件的名字,需要给每一个约束条件命名,方便后续对其索引。此处命名为 "INTERIOR_DISP"。 |
| 128 | + |
| 129 | +#### 3.6.2 监督约束 |
| 130 | + |
| 131 | +由于该案例中自定义了采样方法,因此此处调用监督约束 `SupervisedConstraint`,并将采样点以 input 的形式传递给它: |
| 132 | + |
| 133 | +``` py linenums="95" |
| 134 | +--8<-- |
| 135 | +examples/ntopo/ntopo.py:95:115 |
| 136 | +--8<-- |
| 137 | +``` |
| 138 | + |
| 139 | +`SupervisedConstraint` 的第一个参数是监督约束的读取配置,其中 `dataset` 字段表示使用的训练数据集信息,各个字段分别表示: |
| 140 | + |
| 141 | +1. `name`: 数据集类型,此处 `NamedArrayDataset` 表示从 Array 中读取的数据集; |
| 142 | +2. `input`: Array 类型的输入数据; |
| 143 | + |
| 144 | +注意,其中没有标签值 `label`。 |
| 145 | + |
| 146 | +`sampler` 字段表示采样方法,其中各个字段表示: |
| 147 | + |
| 148 | +1. `name`: 采样器类型,此处 `BatchSampler` 表示批采样器; |
| 149 | +2. `drop_last`: 是否需要丢弃最后无法凑整一个 mini-batch 的样本,设为 False; |
| 150 | +3. `shuffle`: 是否需要在生成样本下标时打乱顺序,设为 True; |
| 151 | + |
| 152 | +`num_workers` 字段表示输入加载时的线程数; |
| 153 | + |
| 154 | +`batch_size` 字段表示 batch 的大小; |
| 155 | + |
| 156 | +第二个参数是损失函数,这里自定义了一个损失函数类,用于接收该案例特殊的批次损失函数 `problem.density_loss_func`; |
| 157 | + |
| 158 | +第三个参数是约束条件的名字,我们需要给每一个约束条件命名,方便后续对其索引。此处命名为 "INTERIOR_DENSITY"。 |
| 159 | + |
| 160 | +### 3.7 可视化器构建 |
| 161 | + |
| 162 | +该案例每隔一定训练间隔,或通过可视化器 `ppsci.visualize.VisualizerVtu`,将优化结果保存为vtu文件: |
| 163 | + |
| 164 | +``` py linenums="130" |
| 165 | +--8<-- |
| 166 | +examples/ntopo/ntopo.py:130:146 |
| 167 | +--8<-- |
| 168 | +``` |
| 169 | + |
| 170 | +### 3.8 其他函数 |
| 171 | + |
| 172 | +如上所述,该案例中需要交替训练两个模型,同时增加了一些技巧,如使用移动平方误差(MMSE)、基于多批次的最佳标准方法(OC)、滤波,因此该案例的训练过程与单一模型训练差距较大。 |
| 173 | + |
| 174 | +因此该案例中根据 PaddleScience 代码,自定义了: |
| 175 | + |
| 176 | +1. `Trainer` 类,该类根据接收的 `solver` 中的信息,定义新的训练过程; |
| 177 | +2. `FunctionalLossBatch` 类,该类基于 `ppsci.loss.base.Loss`,重新定义 loss 处理方式,并在 `Trainer` 中被调用; |
| 178 | +3. `Sampler` 类,该类定义了案例所需的采样方法; |
| 179 | +3. `Plot` 类,对于形状对称的几何,该案例选择仅定义对称部分的一半,然后根据问题中的 `mirror`参数还原完整结果。该类提供了相关处理函数; |
| 180 | + |
| 181 | +具体代码请参考 [完整代码](#4) 中 functions.py 文件。 |
| 182 | + |
| 183 | +### 3.9 模型训练、评估 |
| 184 | + |
| 185 | +完成上述设置之后,将上述实例化的对象按顺序传递给 `ppsci.solver.Solver` 后,按照自定以训练过程进行训练,具体代码请参考 [完整代码](#4) 中 ntopo.py 文件。 |
| 186 | + |
| 187 | +由于拓扑优化问题没有标签,多种优化结果可能都行之有效,因此需要根据可视化结果,人为评估训练结果。 |
| 188 | + |
| 189 | +## 4. 完整代码 |
| 190 | + |
| 191 | +``` py linenums="1" title="ntopo.py" |
| 192 | +--8<-- |
| 193 | +examples/ntopo/ntopo.py |
| 194 | +--8<-- |
| 195 | +``` |
| 196 | + |
| 197 | +``` py linenums="1" title="model.py" |
| 198 | +--8<-- |
| 199 | +examples/ntopo/model.py |
| 200 | +--8<-- |
| 201 | +``` |
| 202 | + |
| 203 | +``` py linenums="1" title="equation.py" |
| 204 | +--8<-- |
| 205 | +examples/ntopo/equation.py |
| 206 | +--8<-- |
| 207 | +``` |
| 208 | + |
| 209 | +``` py linenums="1" title="problems.py" |
| 210 | +--8<-- |
| 211 | +examples/ntopo/problems.py |
| 212 | +--8<-- |
| 213 | +``` |
| 214 | + |
| 215 | +``` py linenums="1" title="functions.py" |
| 216 | +--8<-- |
| 217 | +examples/ntopo/functions.py |
| 218 | +--8<-- |
| 219 | +``` |
| 220 | + |
| 221 | +## 5. 结果展示 |
| 222 | + |
| 223 | +下面展示了不同问题上的优化结果。 |
| 224 | + |
| 225 | +| 序号 | 问题名称 | 预训练模型 | 结果 | |
| 226 | +| :-- | :-- | :-- | :-- | |
| 227 | +| 1 | Beam2D | [beam2d_pretrained.pdparams](https://paddle-org.bj.bcebos.com/paddlescience/models/ntopo/beam2d_pretrained.pdparams) | 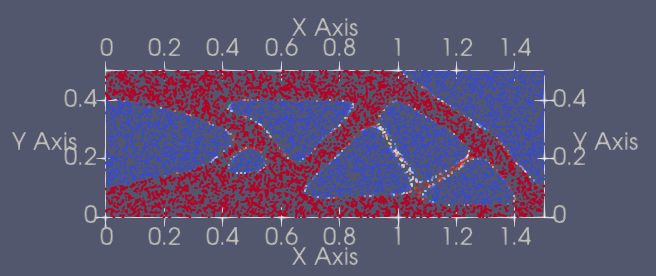 | |
| 228 | +| 2 | Bridge2D |[bridge2d_pretrained.pdparams](https://paddle-org.bj.bcebos.com/paddlescience/models/ntopo/bridge2d_pretrained.pdparams) | 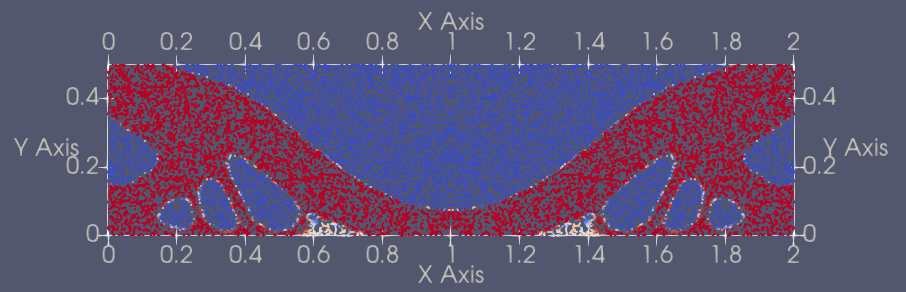 | |
| 229 | +| 3 | Distributed2D | [distributed2d_pretrained.pdparams](https://paddle-org.bj.bcebos.com/paddlescience/models/ntopo/distributed2d_pretrained.pdparams) | 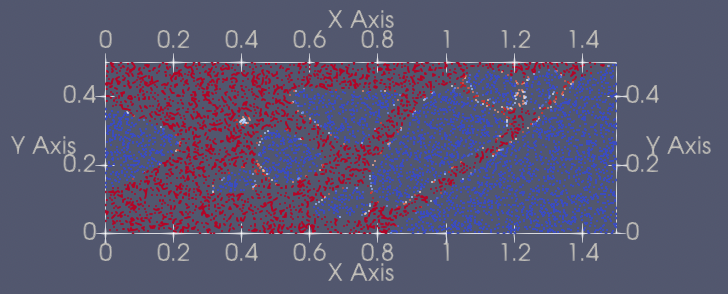 | |
| 230 | +| 4 | LongBeam2D |[longbeam2d_pretrained.pdparams](https://paddle-org.bj.bcebos.com/paddlescience/models/ntopo/longbeam2d_pretrained.pdparams) | 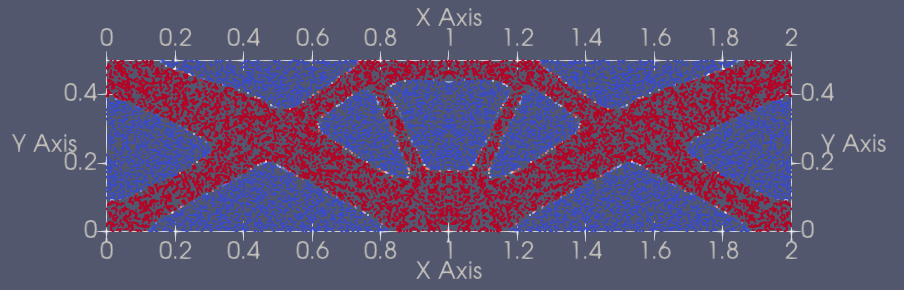 | |
| 231 | +| 5 | LShape2D | [lshape2d_pretrained.pdparams](https://paddle-org.bj.bcebos.com/paddlescience/models/ntopo/lshape2d_pretrained.pdparams) | 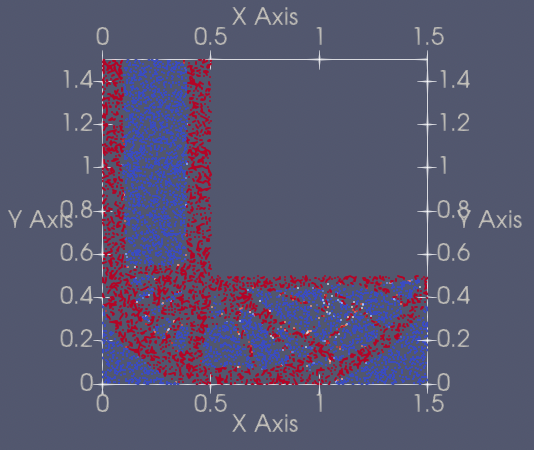 | |
| 232 | +| 6 | Triangle2D |[triangle2d_pretrained.pdparams](https://paddle-org.bj.bcebos.com/paddlescience/models/ntopo/triangle2d_pretrained.pdparams) | 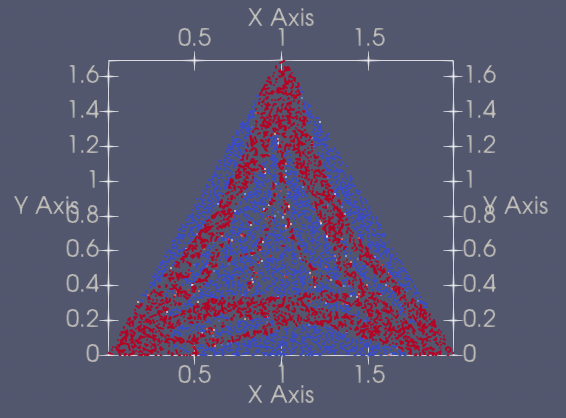 | |
| 233 | +| 7 | TriangleVariants2D | [trianglevariants2d_pretrained.pdparams](https://paddle-org.bj.bcebos.com/paddlescience/models/ntopo/trianglevariants2d_pretrained.pdparams) | 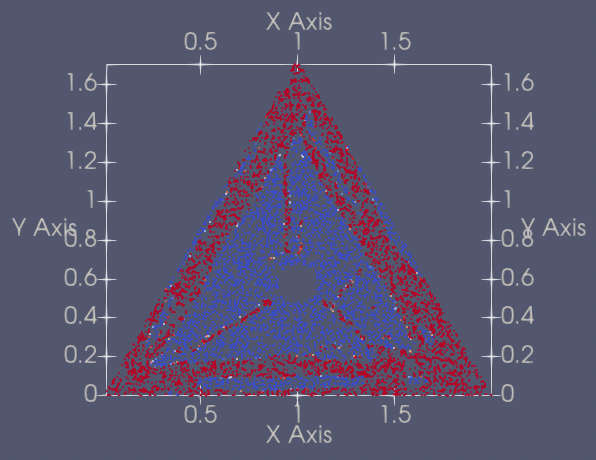 | |
| 234 | +| 8 | Beam3D |[beam3d_pretrained.pdparams](https://paddle-org.bj.bcebos.com/paddlescience/models/ntopo/beam3d_pretrained.pdparams) |  | |
| 235 | +| 9 | Bridge3D |[bridge3d_pretrained.pdparams](https://paddle-org.bj.bcebos.com/paddlescience/models/ntopo/bridge3d_pretrained.pdparams) |  | |
| 236 | + |
| 237 | +## 6. 参考文献 |
| 238 | + |
| 239 | +- [NTopo: Mesh-free Topology Optimization using Implicit Neural Representations](https://arxiv.org/abs/2102.10782) |
| 240 | + |
| 241 | +- [参考代码](https://github.com/JonasZehn/ntopo) |
0 commit comments