Skip to content

Commit f6dc71e

Browse files
Manas2030Manas2030
authored
Do multiple shooting (#505)
* Do multiple shooting * Update DiffEqFlux.jl Included multiple_shooting.jl and exported multiple_shoot method. * Update multiple_shooting.jl Changed the method name to multiple_shoot and also modified the method so that now it returns individual group predictions * Create multiple_shooting.md Added the docs for the multiple_shoot method. * Create multiple_shoot.jl Added test file for src/multiple_shooting.jl * Update multiple_shooting.md Corrected line lengths, added training with BFGS optimizer after ADAM optimizer and changed output image with respect to `grp_size` = 1
1 parent 46811b2 commit f6dc71e

File tree

4 files changed

+260
-0
lines changed

4 files changed

+260
-0
lines changed

‎docs/src/examples/multiple_shooting.md

Lines changed: 118 additions & 0 deletions
Original file line numberDiff line numberDiff line change
@@ -0,0 +1,118 @@
1+
# Multiple Shooting
2+
3+
In Multiple Shooting, the training data is split into overlapping intervals.
4+
The solver is then trained on individual intervals. If the end conditions of any
5+
interval co-incide with the initial conditions of the next immediate interval,
6+
then the joined/combined solution is same as solving on the whole dataset
7+
(without splitting).
8+
9+
To ensure that the overlapping part of two consecutive intervals co-incide,
10+
we add a penalizing term, `continuity_strength * absolute_value_of( prediction
11+
of last point of some group, i - prediction of first point of group i+1 )`, to
12+
the loss.
13+
14+
Note that the `continuity_strength` should have a large positive value to add
15+
high penalities in case the solver predicts discontinuous values.
16+
17+
18+
The following is a working demo, using Multiple Shooting
19+
20+
```julia
21+
using DiffEqFlux, OrdinaryDiffEq, Flux, Optim, Plots
22+
23+
# Define initial conditions and timesteps
24+
datasize = 30
25+
u0 = Float32[2.0, 0.0]
26+
tspan = (0.0f0, 5.0f0)
27+
tsteps = range(tspan[1], tspan[2], length = datasize)
28+
29+
30+
# Get the data
31+
function trueODEfunc(du, u, p, t)
32+
true_A = [-0.1 2.0; -2.0 -0.1]
33+
du .= ((u.^3)'true_A)'
34+
end
35+
prob_trueode = ODEProblem(trueODEfunc, u0, tspan)
36+
ode_data = Array(solve(prob_trueode, Tsit5(), saveat = tsteps))
37+
38+
39+
# Define the Neural Network
40+
dudt2 = FastChain((x, p) -> x.^3,
41+
FastDense(2, 16, tanh),
42+
FastDense(16, 2))
43+
44+
prob_neuralode = NeuralODE(dudt2, (0.0,5.0), Tsit5(), saveat = tsteps)
45+
46+
function plot_function_for_multiple_shoot(plt, pred, grp_size)
47+
step = 1
48+
if(grp_size != 1)
49+
step = grp_size-1
50+
end
51+
if(grp_size == datasize)
52+
scatter!(plt, tsteps, pred[1][1,:], label = "pred")
53+
else
54+
for i in 1:step:datasize-grp_size
55+
# The term `trunc(Integer,(i-1)/(grp_size-1)+1)` goes from 1, 2, ... , N where N is the total number of groups that can be formed from `ode_data` (In other words, N = trunc(Integer, (datasize-1)/(grp_size-1)))
56+
scatter!(plt, tsteps[i:i+step], pred[trunc(Integer,(i-1)/step+1)][1,:], label = "grp"*string(trunc(Integer,(i-1)/step+1)))
57+
end
58+
end
59+
end
60+
61+
callback = function (p, l, pred, predictions; doplot = true)
62+
display(l)
63+
if doplot
64+
# plot the original data
65+
plt = scatter(tsteps[1:size(pred,2)], ode_data[1,1:size(pred,2)], label = "data")
66+
67+
# plot the different predictions for individual shoot
68+
plot_function_for_multiple_shoot(plt, predictions, grp_size_param)
69+
70+
# plot a single shooting performance of our multiple shooting training (this is what the solver predicts after the training is done)
71+
# scatter!(plt, tsteps[1:size(pred,2)], pred[1,:], label = "pred")
72+
73+
display(plot(plt))
74+
end
75+
return false
76+
end
77+
78+
# Define parameters for Multiple Shooting
79+
grp_size_param = 1
80+
loss_multiplier_param = 100
81+
82+
neural_ode_f(u,p,t) = dudt2(u,p)
83+
prob_param = ODEProblem(neural_ode_f, u0, tspan, initial_params(dudt2))
84+
85+
function loss_function_param(ode_data, pred):: Float32
86+
return sum(abs2, (ode_data .- pred))^2
87+
end
88+
89+
function loss_neuralode(p)
90+
return multiple_shoot(p, ode_data, tsteps, prob_param, loss_function_param, grp_size_param, loss_multiplier_param)
91+
end
92+
93+
result_neuralode = DiffEqFlux.sciml_train(loss_neuralode, prob_neuralode.p,
94+
ADAM(0.05), cb = callback,
95+
maxiters = 300)
96+
callback(result_neuralode.minimizer,loss_neuralode(result_neuralode.minimizer)...;doplot=true)
97+
98+
result_neuralode_2 = DiffEqFlux.sciml_train(loss_neuralode, result_neuralode.minimizer,
99+
BFGS(), cb = callback,
100+
maxiters = 100, allow_f_increases=true)
101+
callback(result_neuralode_2.minimizer,loss_neuralode(result_neuralode_2.minimizer)...;doplot=true)
102+
103+
```
104+
Here's the plots that we get from above
105+
106+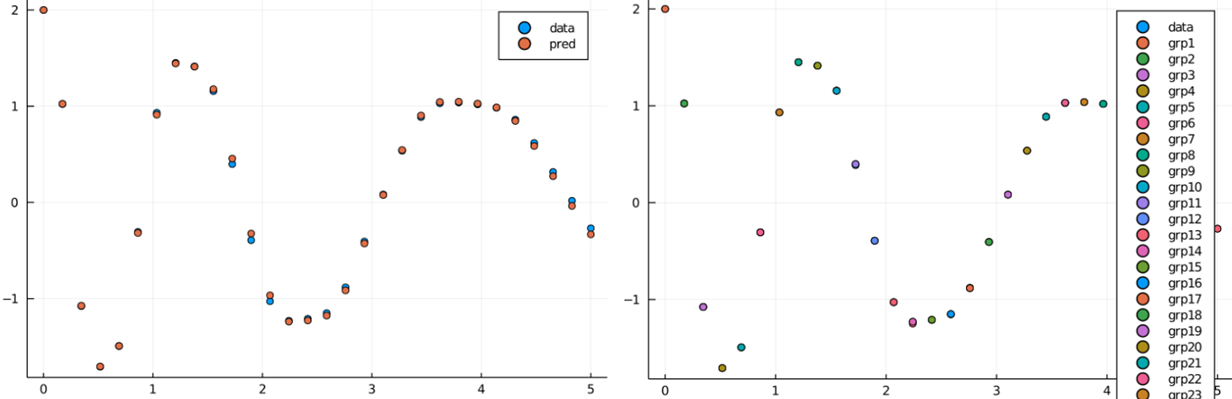
![pic](https://user-images.githubusercontent.com/58384989/111881194-6de9a480-89d5-11eb-8f21-6481d1e22521.PNG)
107+
The picture on the left shows how well our Neural Network does on a single shoot
108+
after training it through `multiple_shoot`.
109+
The picture on the right shows the predictions of each group (Notice that there
110+
are overlapping points as well. These are the points we are trying to co-incide.)
111+
112+
Here is an output with `grp_size` = 30 (which is same as solving on the whole
113+
interval without splitting also called single shooting)
114+
115+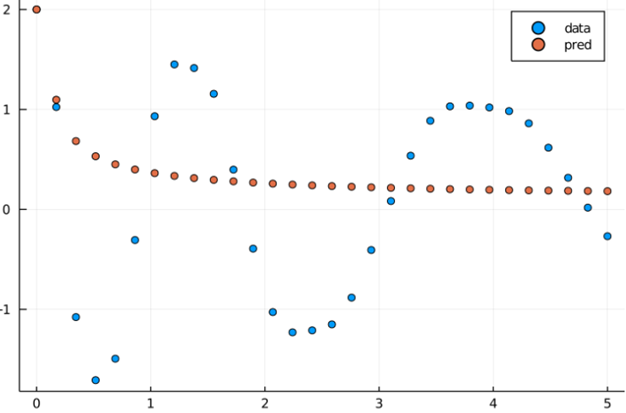
![pic_single_shoot3](https://user-images.githubusercontent.com/58384989/111843307-f0fff180-8926-11eb-9a06-2731113173bc.PNG)
116+
117+
It is clear from the above picture, a single shoot doesn't perform very well
118+
with the ODE Problem we have and gets stuck in a local minima.

‎src/DiffEqFlux.jl

Lines changed: 3 additions & 0 deletions
Original file line numberDiff line numberDiff line change
@@ -82,6 +82,7 @@ include("tensor_product_basis.jl")
8282
include("tensor_product_layer.jl")
8383
include("collocation.jl")
8484
include("hnn.jl")
85+
include("multiple_shooting.jl")
8586

8687
export diffeq_fd, diffeq_rd, diffeq_adjoint
8788
export DeterministicCNF, FFJORD, NeuralODE, NeuralDSDE, NeuralSDE, NeuralCDDE, NeuralDAE, NeuralODEMM, TensorLayer, AugmentedNDELayer, SplineLayer, NeuralHamiltonianDE
@@ -96,4 +97,6 @@ export TriweightKernel, TricubeKernel, GaussianKernel, CosineKernel
9697
export LogisticKernel, SigmoidKernel, SilvermanKernel
9798
export collocate_data
9899

100+
export multiple_shoot
101+
99102
end

‎src/multiple_shooting.jl

Lines changed: 61 additions & 0 deletions
Original file line numberDiff line numberDiff line change
@@ -0,0 +1,61 @@
1+
"""
2+
Returns the a total loss after trying a 'Direct multiple shooting' on ODE data, predictions on the whole ODE data and an array of predictions from the each of the groups (smaller intervals).
3+
In Direct Multiple Shooting, the Neural Network divides the interval into smaller intervals and solves for them separately.
4+
The default group size is 5 implying the whole dataset would be divided in groups of 5 and the Neural Network will solve on them individually.
5+
The default continuity term is 100 implying any losses arising from the non-continuity of 2 different groups will be scaled by 100.
6+
7+
```julia
8+
multiple_shoot(p,ode_data,tsteps,prob,loss_function,grp_size=5,continuity_strength=100)
9+
```
10+
Arguments:
11+
- `p`: The parameters of the Neural Network to be trained.
12+
- `ode_data`: Original Data to be modelled.
13+
- `tsteps`: Timesteps on which ode_data was calculated.
14+
- `prob`: ODE problem that the Neural Network attempts to solve.
15+
- `loss_function`: Any arbitrary function to calculate loss.
16+
- `grp_size`: The group size achieved after splitting the ode_data into equal sizes.
17+
- `continuity_strength`: Multiplying factor to ensure continuity of predictions throughout different groups.
18+
19+
!!!note
20+
The parameter 'continuity_strength' should be a relatively big number to enforce a large penalty whenever the last point of any group doesn't coincide with the first point of next group.
21+
"""
22+
function multiple_shoot(p :: Array, ode_data :: Array, tsteps, prob :: ODEProblem, loss_function ::Function, grp_size :: Integer = 5, continuity_term :: Integer = 100)
23+
datasize = length(ode_data[1,:])
24+
25+
@assert (grp_size >= 1 && grp_size <= datasize) "grp_size can't be <= 1 or >= number of data points"
26+
27+
tot_loss = 0
28+
29+
if(grp_size == datasize)
30+
grp_predictions = [solve(remake(prob, p = p, tspan = (tsteps[1],tsteps[datasize]), u0 = ode_data[:,1]), Tsit5(),saveat = tsteps)]
31+
tot_loss = loss_function(ode_data, grp_predictions[1][:,1:grp_size])
32+
return tot_loss, grp_predictions[1], grp_predictions
33+
end
34+
35+
if(grp_size == 1)
36+
# store individual single shooting predictions for each group
37+
grp_predictions = [solve(remake(prob, p = p, tspan = (tsteps[i],tsteps[i+1]), u0 = ode_data[:,i]), Tsit5(),saveat = tsteps[i:i+1]) for i in 1:datasize-1]
38+
39+
# calculate multiple shooting loss from the single shoots done in above step
40+
for i in 1:datasize-1
41+
tot_loss += loss_function(ode_data[:,i:i+1], grp_predictions[i][:, 1:grp_size]) + (continuity_term * sum(abs,grp_predictions[i][:,2] - ode_data[:,i+1]))
42+
end
43+
44+
# single shooting predictions from ode_data[:,1] (= u0)
45+
pred = solve(remake(prob, p = p, tspan = (tsteps[1],tsteps[datasize]), u0 = ode_data[:,1]), Tsit5(),saveat = tsteps)
46+
return tot_loss, pred, grp_predictions
47+
end
48+
49+
# multiple shooting predictions
50+
grp_predictions = [solve(remake(prob, p = p, tspan = (tsteps[i],tsteps[i+grp_size-1]), u0 = ode_data[:,i]), Tsit5(),saveat = tsteps[i:i+grp_size-1]) for i in 1:grp_size-1:datasize-grp_size]
51+
52+
# calculate multiple shooting loss
53+
for i in 1:grp_size-1:datasize-grp_size
54+
# The term `trunc(Integer,(i-1)/(grp_size-1)+1)` goes from 1, 2, ... , N where N is the total number of groups that can be formed from `ode_data` (In other words, N = trunc(Integer, (datasize-1)/(grp_size-1)))
55+
tot_loss += loss_function(ode_data[:,i:i+grp_size-1], grp_predictions[trunc(Integer,(i-1)/(grp_size-1)+1)][:, 1:grp_size]) + (continuity_term * sum(abs,grp_predictions[trunc(Integer,(i-1)/(grp_size-1)+1)][:,grp_size] - ode_data[:,i+grp_size-1]))
56+
end
57+
58+
# single shooting prediction
59+
pred = solve(remake(prob, p = p, tspan = (tsteps[1],tsteps[datasize]), u0 = ode_data[:,1]), Tsit5(),saveat = tsteps)
60+
return tot_loss, pred, grp_predictions
61+
end

‎test/multiple_shoot.jl

Lines changed: 78 additions & 0 deletions
Original file line numberDiff line numberDiff line change
@@ -0,0 +1,78 @@
1+
using DiffEqFlux, OrdinaryDiffEq, Flux, Optim, Test
2+
3+
# General loss function to compare single shooting and multiple shooting predictions
4+
function general_loss_function(result_neuralode)
5+
return sum(abs2, (ode_data[:,:] .- Array(prob_neuralode(u0, result_neuralode.minimizer)) ))
6+
end
7+
8+
# Define initial conditions and timesteps
9+
datasize = 30
10+
u0 = Float32[2.0, 0.0]
11+
tspan = (0.0f0, 5.0f0)
12+
tsteps = range(tspan[1], tspan[2], length = datasize)
13+
14+
# Get the data
15+
function trueODEfunc(du, u, p, t)
16+
true_A = [-0.1 2.0; -2.0 -0.1]
17+
du .= ((u.^3)'true_A)'
18+
end
19+
prob_trueode = ODEProblem(trueODEfunc, u0, tspan)
20+
ode_data = Array(solve(prob_trueode, Tsit5(), saveat = tsteps))
21+
22+
# Define the Neural Network
23+
dudt2 = FastChain((x, p) -> x.^3,
24+
FastDense(2, 16, tanh),
25+
FastDense(16, 2))
26+
prob_neuralode = NeuralODE(dudt2, (0.0,5.0), Tsit5(), saveat = tsteps)
27+
28+
function loss_neuralode(p)
29+
pred = Array(prob_neuralode(u0, p))
30+
loss = sum(abs2, (ode_data[:,1:size(pred,2)] .- pred))
31+
return loss, pred
32+
end
33+
34+
35+
result_neuralode = DiffEqFlux.sciml_train(loss_neuralode, prob_neuralode.p,
36+
ADAM(0.05),
37+
maxiters = 300)
38+
39+
single_shoot_loss = general_loss_function(result_neuralode)
40+
println("single_shoot_loss: ",single_shoot_loss)
41+
42+
# Define parameters for Multiple Shooting
43+
grp_size_param = 1
44+
loss_multiplier_param = 100
45+
46+
neural_ode_f(u,p,t) = dudt2(u,p)
47+
prob_param = ODEProblem(neural_ode_f, u0, tspan, initial_params(dudt2))
48+
49+
function loss_function_param(ode_data, pred):: Float32
50+
return sum(abs2, (ode_data .- pred))^2
51+
end
52+
53+
function loss_neuralode_param(p)
54+
return multiple_shoot(p, ode_data, tsteps, prob_param, loss_function_param, grp_size_param, loss_multiplier_param)
55+
end
56+
57+
58+
multiple_shoot_result_neuralode_1 = DiffEqFlux.sciml_train(loss_neuralode_param, prob_neuralode.p,
59+
ADAM(0.05),
60+
maxiters = 300)
61+
62+
multiple_shoot_loss_1 = general_loss_function(multiple_shoot_result_neuralode_1)
63+
println("multiple_shoot_loss_1: ",multiple_shoot_loss_1)
64+
65+
66+
# test for grp_size = 1
67+
@test multiple_shoot_loss_1 < single_shoot_loss
68+
69+
# test for grp_size = 5
70+
grp_size_param = 5
71+
multiple_shoot_result_neuralode_2 = DiffEqFlux.sciml_train(loss_neuralode_param, prob_neuralode.p,
72+
ADAM(0.05),
73+
maxiters = 300)
74+
75+
multiple_shoot_loss_2 = general_loss_function(multiple_shoot_result_neuralode_2)
76+
println("multiple_shoot_loss_2: ",multiple_shoot_loss_2)
77+
78+
@test multiple_shoot_loss_2 < single_shoot_loss

0 commit comments

Comments
 (0)