Skip to content

Commit 7d2c43b

Browse files
ChrisRackauckasChrisRackauckas
authored
Merge pull request #1227 from AayushSabharwal/spring-mass-example
Add spring-mass system tutorial
2 parents 8d36632 + 942362d commit 7d2c43b

File tree

2 files changed

+234
-0
lines changed

2 files changed

+234
-0
lines changed

‎docs/make.jl

Lines changed: 1 addition & 0 deletions
Original file line numberDiff line numberDiff line change
@@ -12,6 +12,7 @@ makedocs(
1212
"Home" => "index.md",
1313
"Symbolic Modeling Tutorials" => Any[
1414
"tutorials/ode_modeling.md",
15+
"tutorials/spring_mass.md",
1516
"tutorials/acausal_components.md",
1617
"tutorials/higher_order.md",
1718
"tutorials/tearing_parallelism.md",

‎docs/src/tutorials/spring_mass.md

Lines changed: 233 additions & 0 deletions
Original file line numberDiff line numberDiff line change
@@ -0,0 +1,233 @@
1+
# Component-Based Modeling a Spring-Mass System
2+
3+
In this tutorial we will build a simple component-based model of a spring-mass system. A spring-mass system consists of one or more masses connected by springs. [Hooke's law](https://en.wikipedia.org/wiki/Hooke%27s_law) gives the force exerted by a spring when it is extended or compressed by a given distance. This specifies a differential-equation system where the acceleration of the masses is specified using the forces acting on them.
4+
5+
## Copy-Paste Example
6+
7+
```julia
8+
using ModelingToolkit, Plots, DifferentialEquations, LinearAlgebra
9+
10+
@variables t
11+
D = Differential(t)
12+
13+
function Mass(; name, m = 1.0, xy = [0., 0.], u = [0., 0.])
14+
ps = @parameters m=m
15+
sts = @variables pos[1:2](t)=xy v[1:2](t)=u
16+
eqs = collect(D.(pos) .~ v)
17+
ODESystem(eqs, t, [pos..., v...], ps; name)
18+
end
19+
20+
function Spring(; name, k = 1e4, l = 1.)
21+
ps = @parameters k=k l=l
22+
@variables x(t), dir[1:2](t)
23+
ODESystem(Equation[], t, [x, dir...], ps; name)
24+
end
25+
26+
function connect_spring(spring, a, b)
27+
[
28+
spring.x ~ norm(collect(a .- b))
29+
collect(spring.dir .~ collect(a .- b))
30+
]
31+
end
32+
33+
spring_force(spring) = -spring.k .* collect(spring.dir) .* (spring.x - spring.l) ./ spring.x
34+
35+
m = 1.0
36+
xy = [1., -1.]
37+
k = 1e4
38+
l = 1.
39+
center = [0., 0.]
40+
g = [0., -9.81]
41+
@named mass = Mass(m=m, xy=xy)
42+
@named spring = Spring(k=k, l=l)
43+
44+
eqs = [
45+
connect_spring(spring, mass.pos, center)
46+
collect(D.(mass.v) .~ spring_force(spring) / mass.m .+ g)
47+
]
48+
49+
@named _model = ODESystem(eqs, t)
50+
@named model = compose(_model, mass, spring)
51+
sys = structural_simplify(model)
52+
53+
prob = ODEProblem(sys, [], (0., 3.))
54+
sol = solve(prob, Rosenbrock23())
55+
plot(sol)
56+
```
57+
58+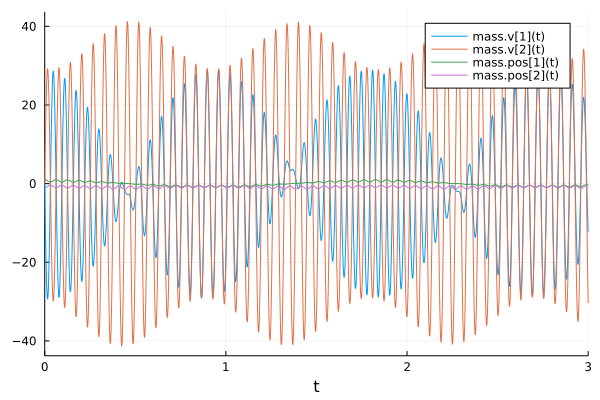
![plotsol](https://user-images.githubusercontent.com/23384717/130322185-52ff1523-4ad8-4b24-94d3-3aa2c4a87082.png)
59+
60+
## Explanation
61+
### Building the components
62+
For each component we use a Julia function that returns an `ODESystem`. At the top, we define the fundamental properties of a `Mass`: it has a mass `m`, a position `pos` and a velocity `v`. We also define that the velocity is the rate of change of position with respect to time.
63+
64+
```julia
65+
function Mass(; name, m = 1.0, xy = [0., 0.], u = [0., 0.])
66+
ps = @parameters m=m
67+
sts = @variables pos[1:2](t)=xy v[1:2](t)=u
68+
eqs = collect(D.(pos) .~ v)
69+
ODESystem(eqs, t, [pos..., v...], ps; name)
70+
end
71+
```
72+
73+
Note that this is an incompletely specified `ODESystem`. It cannot be simulated on its own since the equations for the velocity `v[1:2](t)` are unknown. Notice the addition of a `name` keyword. This allows us to generate different masses with different names. A `Mass` can now be constructed as:
74+
75+
```julia
76+
Mass(name = :mass1)
77+
```
78+
79+
Or using the `@named` helper macro
80+
81+
```julia
82+
@named mass1 = Mass()
83+
```
84+
85+
Next we build the spring component. It is characterised by the spring constant `k` and the length `l` of the spring when no force is applied to it. The state of a spring is defined by its current length and direction.
86+
87+
```julia
88+
function Spring(; name, k = 1e4, l = 1.)
89+
ps = @parameters k=k l=l
90+
@variables x(t), dir[1:2](t)
91+
ODESystem(Equation[], t, [x, dir...], ps; name)
92+
end
93+
```
94+
95+
We now define functions that help construct the equations for a mass-spring system. First, the `connect_spring` function connects a `spring` between two positions `a` and `b`. Note that `a` and `b` can be the `pos` of a `Mass`, or just a fixed position such as `[0., 0.]`. In that sense, the length of the spring `x` is given by the length of the vector `dir` joining `a` and `b`.
96+
97+
```julia
98+
function connect_spring(spring, a, b)
99+
[
100+
spring.x ~ norm(collect(a .- b))
101+
collect(spring.dir .~ collect(a .- b))
102+
]
103+
end
104+
```
105+
106+
Lastly, we define the `spring_force` function that takes a `spring` and returns the force exerted by this spring.
107+
108+
```julia
109+
spring_force(spring) = -spring.k .* collect(spring.dir) .* (spring.x - spring.l) ./ spring.x
110+
```
111+
112+
To create our system, we will first create the components: a mass and a spring. This is done as follows:
113+
114+
```julia
115+
m = 1.0
116+
xy = [1., -1.]
117+
k = 1e4
118+
l = 1.
119+
center = [0., 0.]
120+
g = [0., -9.81]
121+
@named mass = Mass(m=m, xy=xy)
122+
@named spring = Spring(k=k, l=l)
123+
```
124+
125+
We can now create the equations describing this system, by connecting `spring` to `mass` and a fixed point.
126+
127+
```julia
128+
eqs = [
129+
connect_spring(spring, mass.pos, center)
130+
collect(D.(mass.v) .~ spring_force(spring) / mass.m .+ g)
131+
]
132+
```
133+
134+
Finally, we can build the model using these equations and components.
135+
136+
```julia
137+
@named _model = ODESystem(eqs, t)
138+
@named model = compose(_model, mass, spring)
139+
```
140+
141+
We can take a look at the equations in the model using the `equations` function.
142+
143+
```julia
144+
equations(model)
145+
146+
7-element Vector{Equation}:
147+
Differential(t)(mass₊v[1](t)) ~ -spring₊k*spring₊dir[1](t)*(mass₊m^-1)*(spring₊x(t) - spring₊l)*(spring₊x(t)^-1)
148+
Differential(t)(mass₊v[2](t)) ~ -9.81 - (spring₊k*spring₊dir[2](t)*(mass₊m^-1)*(spring₊x(t) - spring₊l)*(spring₊x(t)^-1))
149+
spring₊x(t) ~ sqrt(abs2(mass₊pos[1](t)) + abs2(mass₊pos[2](t)))
150+
spring₊dir[1](t) ~ mass₊pos[1](t)
151+
spring₊dir[2](t) ~ mass₊pos[2](t)
152+
Differential(t)(mass₊pos[1](t)) ~ mass₊v[1](t)
153+
Differential(t)(mass₊pos[2](t)) ~ mass₊v[2](t)
154+
```
155+
156+
The states of this model are:
157+
158+
```julia
159+
states(model)
160+
161+
7-element Vector{Term{Real, Base.ImmutableDict{DataType, Any}}}:
162+
mass₊v[1](t)
163+
mass₊v[2](t)
164+
spring₊x(t)
165+
mass₊pos[1](t)
166+
mass₊pos[2](t)
167+
spring₊dir[1](t)
168+
spring₊dir[2](t)
169+
```
170+
171+
And the parameters of this model are:
172+
173+
```julia
174+
parameters(model)
175+
176+
6-element Vector{Sym{Real, Base.ImmutableDict{DataType, Any}}}:
177+
spring₊k
178+
mass₊m
179+
spring₊l
180+
mass₊m
181+
spring₊k
182+
spring₊l
183+
```
184+
185+
### Simplifying and solving this system
186+
187+
This system can be solved directly as a DAE using [one of the DAE solvers from DifferentialEquations.jl](https://diffeq.sciml.ai/stable/solvers/dae_solve/). However, we can symbolically simplify the system first beforehand. Running `structural_simplify` eliminates unnecessary variables from the model to give the leanest numerical representation of the system.
188+
189+
```julia
190+
sys = structural_simplify(model)
191+
equations(sys)
192+
193+
4-element Vector{Equation}:
194+
Differential(t)(mass₊v[1](t)) ~ -spring₊k*mass₊pos[1](t)*(mass₊m^-1)*(sqrt(abs2(mass₊pos[1](t)) + abs2(mass₊pos[2](t))) - spring₊l)*(sqrt(abs2(mass₊pos[1](t)) + abs2(mass₊pos[2](t)))^-1)
195+
Differential(t)(mass₊v[2](t)) ~ -9.81 - (spring₊k*mass₊pos[2](t)*(mass₊m^-1)*(sqrt(abs2(mass₊pos[1](t)) + abs2(mass₊pos[2](t))) - spring₊l)*(sqrt(abs2(mass₊pos[1](t)) + abs2(mass₊pos[2](t)))^-1))
196+
Differential(t)(mass₊pos[1](t)) ~ mass₊v[1](t)
197+
Differential(t)(mass₊pos[2](t)) ~ mass₊v[2](t)
198+
```
199+
200+
We are left with only 4 equations involving 4 state variables (`mass.pos[1]`, `mass.pos[2]`, `mass.v[1]`, `mass.v[2]`). We can solve the system by converting it to an `ODEProblem` in mass matrix form and solving with an [`ODEProblem` mass matrix solver](https://diffeq.sciml.ai/stable/solvers/dae_solve/#OrdinaryDiffEq.jl-(Mass-Matrix)). This is done as follows:
201+
202+
```julia
203+
prob = ODEProblem(sys, [], (0., 3.))
204+
sol = solve(prob, Rosenbrock23())
205+
plot(sol)
206+
```
207+
208+
What if we want the timeseries of a different variable? That information is not lost! Instead, `structural_simplify` simply changes state variables into `observed` variables.
209+
210+
```julia
211+
observed(sys)
212+
213+
3-element Vector{Equation}:
214+
spring₊dir[2](t) ~ mass₊pos[2](t)
215+
spring₊dir[1](t) ~ mass₊pos[1](t)
216+
spring₊x(t) ~ sqrt(abs2(mass₊pos[1](t)) + abs2(mass₊pos[2](t)))
217+
```
218+
219+
These are explicit algebraic equations which can be used to reconstruct the required variables on the fly. This leads to dramatic computational savings since implicitly solving an ODE scales as O(n^3), so fewer states are signficantly better!
220+
221+
We can access these variables using the solution object. For example, let's retrieve the x-position of the mass over time:
222+
223+
```julia
224+
sol[mass.pos[1]]
225+
```
226+
227+
We can also plot the path of the mass:
228+
229+
```julia
230+
plot(sol, vars = (mass.pos[1], mass.pos[2]))
231+
```
232+
233+
![plotpos](https://user-images.githubusercontent.com/23384717/130322197-cff35eb7-0739-471d-a3d9-af83d87f1cc7.png)

0 commit comments

Comments
 (0)