finalize comments

Author: ChrisRackauckas

docs/src/tutorials/ode_modeling.md

@@ -37,10 +37,8 @@ D = Differential(t) # define an operator for the differentiation w.r.t. time
 ```
 
 Note that equations in MTK use the tilde character (`~`) as equality sign.
-The `@named` macro just adds the keyword-argument `name` to the call of
-`ODESystem`. Its value is the name of the variable the system is assigned to.
-For this example, calling `fol_model = ODESystem(...; name=:fol_model)` would do
-exactly the same.
+Also note that the `@named` macro simply ensures that the symbolic name
+matches the name in the REPL. If omitted, you can directly set the `name` keyword.
 
 After construction of the ODE, you can solve it using [DifferentialEquations.jl](https://diffeq.sciml.ai/):
 
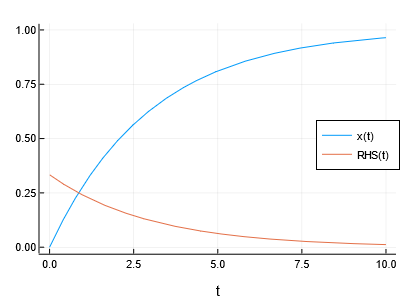
@@ -107,6 +105,10 @@ plot(sol, vars=[x, RHS])
 
 ![Simulation result of first-order lag element, with right-hand side](https://user-images.githubusercontent.com/13935112/111958403-7e8d3e00-8aed-11eb-9d18-08b5180a59f9.png)
 
+Note that similarly the indexing of the solution works via the names, and so
+`sol[x]` gives the timeseries for `x`, `sol[x,2:10]` gives the 2nd through 10th
+values of `x` matching `sol.t`, etc. Note that this works even for variables
+which have been eliminated, and thus `sol[RHS]` retrieves the values of `RHS`.
 
 ## Specifying a time-variable forcing function
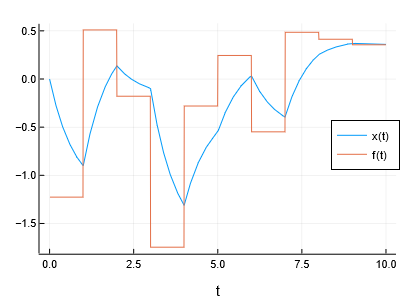
 What if the forcing function (the "external input") ``f(t)`` is not constant?
@@ -133,18 +135,15 @@ f_fun(t) = t >= 10 ? value_vector[end] : value_vector[Int(floor(t))+1]
 @named fol_external_f = ODESystem([f ~ f_fun(t), D(x) ~ (f - x)/τ])
 prob = ODEProblem(structural_simplify(fol_external_f), [x => 0.0], (0.0,10.0), [τ => 0.75])
 
-using DifferentialEquations: Rodas4
-sol = solve(prob, Rodas4())
+sol = solve(prob)
 plot(sol, vars=[x,f])
 ```
 
 ![Simulation result of first-order lag element, step-wise forcing function](https://user-images.githubusercontent.com/13935112/111958424-83ea8880-8aed-11eb-8f42-489f4b44c3bc.png)
 
 
-Note that for this problem, the implicit solver `Rodas4` is used, to cleanly resolve
-the steps in the forcing function.
-
 ## Building component-based, hierarchical models
+
 Working with simple one-equation systems is already fun, but composing more complex systems from
 simple ones is even more fun. Best practice for such a "modeling framework" could be to use
 
@@ -275,6 +274,7 @@ partial derivatives, are not used. Let's benchmark this (`prob` still is the pro
 
 ```julia
 using BenchmarkTools
+using DifferentialEquations: Rodas4
 
 @btime solve(prob, Rodas4());
       # 251.300 μs (873 allocations: 31.18 KiB)
@@ -293,7 +293,9 @@ prob_an = ODEProblem(connected_simp, u0, (0.0,10.0), p; jac=true, sparse=true)
 The speedup is significant. For this small dense model (3 of 4 entries are populated), using sparse matrices is counterproductive in terms of required memory allocations. For large,
 
 hierarchically built models, which tend to be sparse, speedup and the reduction of
-memory allocation can be expected to be substantial.
+memory allocation can be expected to be substantial. In addition, these problem
+builders allow for automatic parallelism using the structural information. For
+more information, see the [ODESystem](@ref ODESystem) page.
 
 ## Notes and pointers how to go on
 Here are some notes that may be helpful during your initial steps with MTK: