You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
This project is under development at the moment. The implementation of potential calculations is fairly experimental and has not been extensively verified yet.
7
-
You can test simulation of different systems now but be aware of possible changes in future.
7
+
You can test simulation of different systems now but be aware of possible changes in the future.
8
8
9
9
## Add Package
10
10
@@ -15,12 +15,12 @@ In order to start simulating systems of N interacting bodies, it is necessary to
15
15
using NBodySimulator
16
16
```
17
17
18
-
If you cannot wait to start codding, try to run some scripts from `examples` folder. The number of particles `N` and the final timestep of simulations `t2` are the two parameters which will determine the time of script execution.
18
+
If you cannot wait to start coding, try to run some scripts from the`examples` folder. The number of particles `N` and the final timestep of simulations `t2` are the two parameters which will determine the time of script execution.
19
19
20
20
## Basic Components
21
-
There are three basic components required for any simulation of systems of N-bodies: `bodies`, `system` and `simulation`.
21
+
There are three basic components required for any simulation of systems of N-bodies: `bodies`, `system`, and `simulation`.
22
22
23
-
**Bodies** or **Particles** are the objects which will interact with each other and for which the equations of Newton's 2nd law are solved during the simulation process. Three parameters of a body are necessary, they are initial location, initial velocity and mass. `MassBody` structure represents such particles:
23
+
**Bodies** or **Particles** are the objects which will interact with each other and for which the equations of Newton's 2nd law are solved during the simulation process. Three parameters of a body are necessary, namely: initial location, initial velocity, and mass. `MassBody` structure represents such particles:
24
24
25
25
```julia
26
26
using StaticArrays
@@ -29,7 +29,7 @@ v = SVector(.1,.2,.5)
29
29
mass =1.25
30
30
body =MassBody(r,v,mass)
31
31
```
32
-
For the sake of simulation speed it is advised to use [static arrays](https://github.com/JuliaArrays/StaticArrays.jl).
32
+
For the sake of simulation speed, it is advised to use [static arrays](https://github.com/JuliaArrays/StaticArrays.jl).
33
33
34
34
A **System** covers bodies and necessary parameters for correct simulation of interaction between particles. For example, to create an entity for a system of gravitationally interacting particles, one needs to use `GravitationalSystem` constructor:
35
35
@@ -38,7 +38,7 @@ const G = 6.67e-11 # m^3/kg/s^2
38
38
system =GravitationalSystem(bodies, G)
39
39
```
40
40
41
-
**Simulation** is an entity determining parameters of the experiment: time span of simulation, global physical constants, borders of the simulation cell, external magnetic or electric fields, etc. The required arguments for `NBodySImulation` constructor are the system to be tested and the time span of simulation.
41
+
**Simulation** is an entity determining parameters of the experiment: time span of simulation, global physical constants, borders of the simulation cell, external magnetic or electric fields, etc. The required arguments for `NBodySImulation` constructor are the system to be tested and the time span of the simulation.
The Lennard-Jones potential is used in molecular dynamics simulations for approximating interactions between neutral atoms or molecules. The [SPC/Fw water model](http://www.sklogwiki.org/SklogWiki/index.php/SPC/Fw_model_of_water) is used in water simulations. The meaning of arguments for `SPCFwParameters` constructor will be clarified further in this documentation.
81
81
82
-
`PotentialNBodySystem` structure represents systems with a custom set of potentials. In other words, the user determines the ways in which the particles are allowed to interact. One can pass the bodies and parameters of interaction potentials into that system. In case the potential parameters are not set, during the simulation particles will move at constant velocities without acceleration.
82
+
`PotentialNBodySystem` structure represents systems with a custom set of potentials. In other words, the user determines the ways in which the particles are allowed to interact. One can pass the bodies and parameters of interaction potentials into that system. In the case the potential parameters are not set, the particles will move at constant velocities without acceleration during the simulation.
83
83
84
84
```julia
85
85
system =PotentialNBodySystem(bodies, Dict(:gravitational=> g_parameters, electrostatic:=> el_potential))
86
86
```
87
87
88
88
### Custom Potential
89
-
There exists an [example](http://docs.juliadiffeq.org/dev/models/physical.html) of simulation of an N-body system at absolutely custom potential.
89
+
There exists an [example](http://docs.juliadiffeq.org/dev/models/physical.html) of a simulation of an N-body system at absolutely custom potential.
90
90
91
91
Here is shown how to create custom acceleration functions using tools of NBodySimulator.
Next, the acceleration function for the potential is required. The custom potential defined here creates a force acting on all the particles proportionate to their masses. The first argument of the function determines the potential for which the acceleration should be calculated in this method.
101
+
Next, the acceleration function for the potential is required. The custom potential defined here creates a force acting on all the particles proportionate to their masses. The first argument of the function determines the potential for which the acceleration should be calculated in this method.
(dv, u, v, t, i) ->begin custom_accel =SVector(0.0, 0.0, p.a); dv .= custom_accel*ms[i] end
107
+
(dv, u, v, t, i) ->begin custom_accel =SVector(0.0, 0.0, p.a); dv .= custom_accel*ms[i] end
108
108
end
109
109
```
110
110
111
-
After the parameters and acceleration function are created, one can instantiate a system of particles interacting with a set of potentials which includes the justcreated custom potential:
111
+
After the parameters and acceleration function have been created, one can instantiate a system of particles interacting with a set of potentials which includes the just-created custom potential:
112
112
113
113
```julia
114
114
parameters =CustomPotentialParameters(-9.8)
115
115
system =PotentialNBodySystem(bodies, Dict(:custom_potential_params=> parameters))
116
116
```
117
117
118
118
### Gravitational Interaction
119
-
Using NBodySimulator it is possible to simulate gravitational interaction of celestial bodies.
119
+
Using NBodySimulator, it is possible to simulate gravitational interaction of celestial bodies.
120
120
In fact, any structure for bodies can be used for simulation of gravitational interaction since all those structures are required to have mass as one of their parameters:
Interaction between charged particles obeys Coulomb's law. The movement of such bodies can be simulated using `ChargedParticle` and `ChargedParticles` structures.
161
161
162
-
The following example shows how to model two oppositely charged particles. If one body is more massive that another, it will be possible to observe rotation of the light body around the heavy one without adjusting their positions in space. The constructor for `ChargedParticles` system requires bodies and Coulomb's constant `k` to be passed as arguments.
162
+
The following example shows how to model two oppositely charged particles. If one body is more massive than another, it will be possible to observe rotation of the light body around the heavy one without adjusting their positions in space. The constructor for the`ChargedParticles` system requires bodies and Coulomb's constant `k` to be passed as arguments.
An N-body system consisting of `MagneticParticle`s can be used for simulation of interacting magnetic dipoles, though such dipoles cannot rotate in space. Such a model can represent single domain particles interacting under the influence of a strong external magnetic field.
181
181
182
-
In order to create a magnetic particle, one specifies its location in space, velocity and the vector of its magnetic moment. The following code shows how we can construct an iron particle:
182
+
In order to create a magnetic particle, one specifies its location in space, velocity, and the vector of its magnetic moment. The following code shows how we can construct an iron particle:
To calculate magnetic interactions properly one should also specify the value for the constant μ<sub>0</sub>/4π or its substitute. Having created parameters for the magnetostatic potential, one can now instantiate a system of particles which should interact magnetically. For that purpose we use `PotentialNBodySystem` and pass particles and potential parameters as arguments.
202
+
To calculate magnetic interactions properly, one should also specify the value for the constant μ<sub>0</sub>/4π or its substitute. Having created parameters for the magnetostatic potential, one can now instantiate a system of particles which should interact magnetically. For that purpose, we use `PotentialNBodySystem` and pass particles and potential parameters as arguments.
NBodySimulator allows one to conduct molecular dynamic simulations for the Lennard-Jones liquids, SPC/Fw model of water and other molecular systems thanks to implementations of basic interaction potentials between atoms and molecules:
212
+
NBodySimulator allows one to conduct molecular dynamic simulations for the Lennard-Jones liquids, SPC/Fw model of water, and other molecular systems thanks to implementations of basic interaction potentials between atoms and molecules:
213
213
214
214
- Lennard-Jones
215
215
- electrostatic and magnetostatic
216
216
- harmonic bonds
217
-
- harmonic valence angle generated by pairs of bonds
217
+
- harmonic valence angle generated by pairs of bonds
218
218
219
-
The comprehensive examples of liquid argon and water simulations can be found in `examples` folder.
219
+
The comprehensive examples of liquid argon and water simulations can be found in the `examples` folder.
220
220
Here only the basic principles of the molecular dynamics simulations using NBodySimulator are presented using liquid argon as a classical MD system for beginners.
221
221
222
222
First of all, one needs to define parameters of the simulation:
@@ -244,7 +244,7 @@ Liquid argon consists of neutral molecules so the Lennard-Jones potential runs t
The default boundary conditions are `InfiniteBox` without any limits, default thermostat is `NullThermostat` which does no thermostating and default Boltzmann constant `kb` equals its value in SI, i.e. 1.38e-23 J/K.
267
+
The default boundary conditions are `InfiniteBox` without any limits, default thermostat is `NullThermostat`(which does no thermostating), and the default Boltzmann constant `kb` equals its value in SI, i.e., 1.38e-23 J/K.
268
268
269
269
## Water Simulations
270
-
In NBodySImulator the [SPC/Fw water model](http://www.sklogwiki.org/SklogWiki/index.php/SPC/Fw_model_of_water) is implemented. For using this model, one has to specify parameters of the Lennard-Jones potential between the oxygen atoms of water molecules, parameters of the electrostatic potential for the corresponding interactions between atoms of different molecules and parameters for harmonic potentials representing bonds between atoms and the valence angle made from bonds between hydrogen atoms and the oxygen one.
270
+
In NBodySImulator the [SPC/Fw water model](http://www.sklogwiki.org/SklogWiki/index.php/SPC/Fw_model_of_water) is implemented. For using this model, one has to specify parameters of the Lennard-Jones potential between the oxygen atoms of water molecules, parameters of the electrostatic potential for the corresponding interactions between atoms of different molecules and parameters for harmonic potentials representing bonds between atoms and the valence angle made from bonds between hydrogen atoms and the oxygen atom.
For each water molecule here, `rOH` is the equilibrium distance between a hydrogen atom and the oxygen atom, `∠HOH` denotes the equilibrium angle made of those two bonds, `k_bond` and `k_angle` are the elastic coefficients for the corresponding harmonic potentials.
281
281
282
-
Further, one pass the water system into `NBodySimulation` constructor as a usual system of N-bodies.
282
+
Further, one can pass the water system into the`NBodySimulation` constructor as a usual system of N-bodies.
Usually during simulation of a system is required to be at a particular temperature. NBodySimulator contains several thermostats for that purpose. Here the thermostating of liquid argon is presented, for thermostating of water one can refer to [this post](https://mikhail-vaganov.github.io/gsoc-2018-blog/2018/08/06/thermostating.html)
289
+
Usually, during the simulation, a system is required to be at a particular temperature. NBodySimulator contains several thermostats for that purpose. Here the thermostating of liquid argon is presented, for thermostating of water one can refer to [this post](https://mikhail-vaganov.github.io/gsoc-2018-blog/2018/08/06/thermostating.html)
Once the simulation is completed, one can analyze the result and obtain some useful characteristics of the system.
322
+
Once the simulation is completed, one can analyze the result and obtain some useful characteristics of the system.
323
323
324
-
Function `run_simulation` returns a structure containing the initial parameters of simulation and the solution of differential equation (DE) required for description of the corresponding system of particles. There are different functions which help to interpret solution of DEs into physical quantities.
324
+
The function `run_simulation` returns a structure containing the initial parameters of the simulation and the solution of the differential equation (DE) required for the description of the corresponding system of particles. There are different functions which help to interpret the solution of DEs into physical quantities.
325
325
326
326
One of the main characteristics of a system during molecular dynamics simulations is its thermodynamic temperature. The value of the temperature at a particular time `t` can be obtained via calling this function:
327
327
328
328
```julia
329
-
T =temperature(result, t)
329
+
T =temperature(result, t)
330
330
```
331
331
332
-
### [Radial distribution functions](https://en.wikipedia.org/wiki/Radial_distribution_function)
332
+
### [Radial distribution functions](https://en.wikipedia.org/wiki/Radial_distribution_function)
333
333
The RDF is another popular and essential characteristic of molecules or similar systems of particles. It shows the reciprocal location of particles averaged by the time of simulation.
334
334
335
335
```julia
@@ -346,35 +346,35 @@ The MSD characteristic can be used to estimate the shift of particles from their
346
346
```julia
347
347
(ts, dr2) =msd(result)
348
348
```
349
-
For a standard liquid argon system the displacement grows with time:
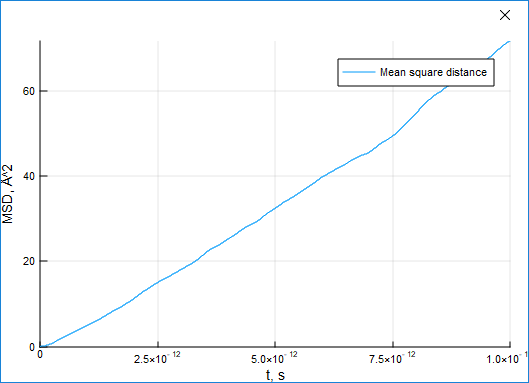
349
+
For a standard liquid argon system, the displacement grows with time:
350
350
351
351
352
352
### Energy Functions
353
353
354
354
Energy is a highly important physical characteristic of a system. The module provides four functions to obtain it, though the `total_energy` function just sums potential and kinetic energy:
355
355
356
356
```julia
357
-
e_init =initial_energy(simualtion)
357
+
e_init =initial_energy(simulation)
358
358
e_kin =kinetic_energy(result, t)
359
359
e_pot =potential_energy(result, t)
360
360
e_tot =total_energy(result, t)
361
361
```
362
362
363
363
## Plotting Images
364
-
Using tools of NBodySimulator one can export results of simulation into a [Protein Database File](https://en.wikipedia.org/wiki/Protein_Data_Bank_(file_format)). [VMD](http://www.ks.uiuc.edu/Research/vmd/) is a well-known tool for visualizing molecular dynamics, which can read data from PDB files.
364
+
Using tools of NBodySimulator, one can export the results of a simulation into a [Protein Database File](https://en.wikipedia.org/wiki/Protein_Data_Bank_(file_format)). [VMD](http://www.ks.uiuc.edu/Research/vmd/) is a well-known tool for visualizing molecular dynamics, which can read data from PDB files.
In future it will be possible to export results via FileIO interface and its `save` function.
370
+
In the future it will be possible to export results via FileIO interface and its `save` function.
371
371
372
-
Using Plots.jl one can draw positions of particles at any time of simulation or create an animation of moving particles, molecules of water:
372
+
Using Plots.jl, one can draw positions of particles at any time of simulation or create an animation of moving particles, molecules of water:
373
373
374
374
```julia
375
375
using Plots
376
376
plot(result)
377
377
animate(result, "path_to_file.gif")
378
378
```
379
379
380
-
Makie.jl also has a recipe for plotting results of N-body simulations. The [example](http://makie.juliaplots.org/stable/examples-meshscatter.html#Type-recipe-for-molecule-simulation-1) is presented in the documentation.
380
+
Makie.jl also has a recipe for plotting the results of N-body simulations. The [example](http://makie.juliaplots.org/stable/examples-meshscatter.html#Type-recipe-for-molecule-simulation-1) is presented in the documentation.
0 commit comments