You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
Copy file name to clipboardExpand all lines: README.md
+22-13Lines changed: 22 additions & 13 deletions
Display the source diff
Display the rich diff
Original file line number
Diff line number
Diff line change
@@ -1,17 +1,21 @@
1
+
<divstyle="text-align: center;"align="center">
2
+
3
+
<imgclass="dark-light"width="98"height="85"alt="s2fft logo - schematic representation of a tiled sphere"src="https://raw.githubusercontent.com/astro-informatics/s2fft/main/docs/assets/sax_logo.png">
4
+
5
+
# Differentiable and accelerated spherical transforms
[](https://colab.research.google.com/github/astro-informatics/s2fft/blob/main/notebooks/spherical_harmonic_transform.ipynb)
<imgalign="left"height="85"width="98"alt="s2fft logo - schematic representation of a tiled sphere"src="https://raw.githubusercontent.com/astro-informatics/s2fft/main//docs/assets/sax_logo.png">
13
-
14
-
# Differentiable and accelerated spherical transforms
18
+
</div>
15
19
16
20
`S2FFT` is a Python package for computing Fourier transforms on the sphere
17
21
and rotation group [(Price & McEwen 2024)](https://arxiv.org/abs/2311.14670) using
@@ -24,7 +28,6 @@ for adjoint transformations where needed, and comes with different
24
28
optimisations (precompute or not) that one may select depending on
25
29
available resources and desired angular resolution $L$.
26
30
27
-
28
31
## Algorithms ⚡
29
32
30
33
`S2FFT` leverages new algorithmic structures that can he highly
@@ -34,7 +37,10 @@ algorithms are based on new Wigner-d recursions that are stable to high
34
37
angular resolution $L$. The diagram below illustrates the recursions
35
38
(for further details see [Price & McEwen 2024]((https://arxiv.org/abs/2311.14670))).
36
39
37
-
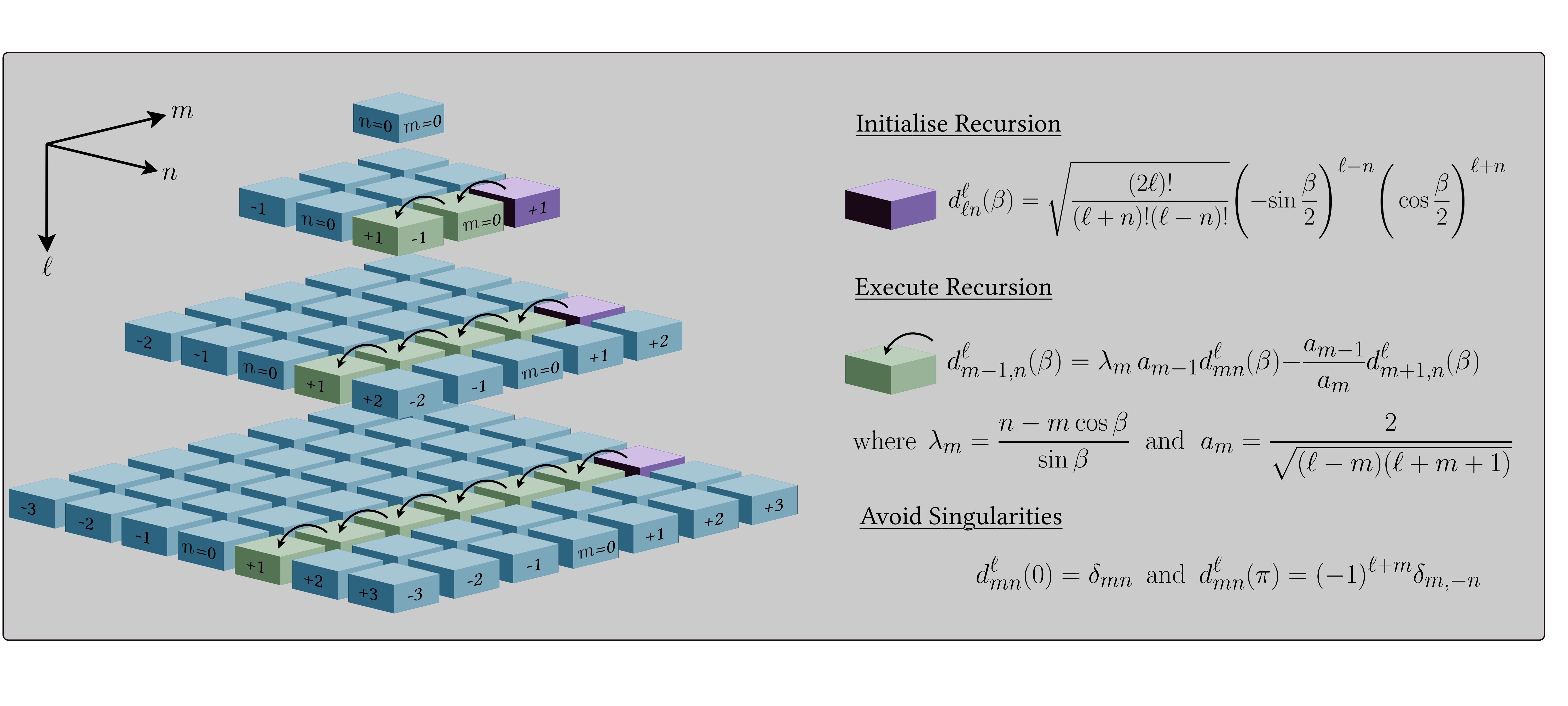
40
+
<divstyle="text-align: center;"align="center">
41
+
<imgclass="dark-light"alt="Schematic of Wigner recursions"src="https://raw.githubusercontent.com/astro-informatics/s2fft/main/docs/assets/figures/Wigner_recursion_legend_darkmode.png" />
42
+
</div>
43
+
38
44
With this recursion to hand, the spherical harmonic coefficients of an
39
45
isolatitudinally sampled map may be computed as a two step process. First,
40
46
a 1D Fourier transform over longitude, for each latitudinal ring. Second,
@@ -47,7 +53,9 @@ negligible memory overhead at the cost of slightly slower execution. The
47
53
diagram below illustrates the separable spherical harmonic transform
48
54
(for further details see [Price & McEwen 2024]((https://arxiv.org/abs/2311.14670))).
49
55
50
-
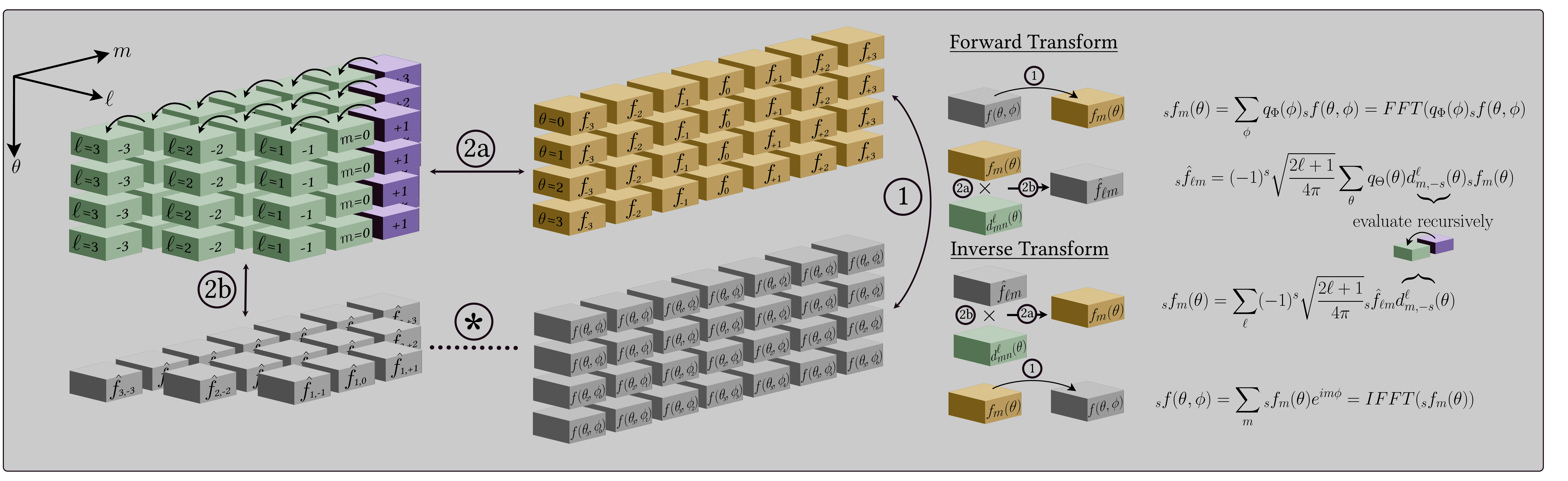
56
+
<divstyle="text-align: center;"align="center">
57
+
<imgclass="dark-light"alt="Schematic of forward and inverse spherical harmonic transforms"src="https://raw.githubusercontent.com/astro-informatics/s2fft/main/docs/assets/figures/sax_schematic_legend_darkmode.png" />
58
+
</div>
51
59
52
60
## Sampling 🌍
53
61
@@ -72,7 +80,9 @@ so the corresponding harmonic transforms do not achieve machine
72
80
precision but exhibit some error. However, the HEALPix sampling provides
73
81
pixels of equal areas, which has many practical advantages.
74
82
75
-
<palign="center"><imgalt="Visualization of spherical sampling schemes"src="https://raw.githubusercontent.com/astro-informatics/s2fft/main/docs/assets/figures/spherical_sampling.png"width="700"></p>
83
+
<divstyle="text-align: center;"align="center">
84
+
<imgclass="dark-light"alt="Visualization of spherical sampling schemes"src="https://raw.githubusercontent.com/astro-informatics/s2fft/main/docs/assets/figures/spherical_sampling.png"width="700">
85
+
</div>
76
86
77
87
> [!NOTE]
78
88
> For algorithmic reasons JIT compilation of HEALPix transforms can become slow at high bandlimits, due to XLA unfolding of loops which currently cannot be avoided. After compiling HEALPix transforms should execute with the efficiency outlined in the associated paper, therefore this additional time overhead need only be incurred once. We are aware of this issue and are working to fix it. A fix for CPU execution has now been implemented (see example [notebook](https://astro-informatics.github.io/s2fft/tutorials/spherical_harmonic/JAX_HEALPix_backend.html)).
@@ -181,7 +191,7 @@ For further details on usage see the [documentation](https://astro-informatics.g
181
191
> [!NOTE]
182
192
> We also provide PyTorch support for the precompute version of our transforms, as demonstrated in the [_Torch frontend_ tutorial notebook](https://astro-informatics.github.io/s2fft/tutorials/torch_frontend/torch_frontend.html).
183
193
184
-
## JAX wrappers for SSHT and HEALPix 💡
194
+
## SSHT & HEALPix wrappers 💡
185
195
186
196
`S2FFT` also provides JAX support for existing C/C++ packages, specifically [`HEALPix`](https://healpix.jpl.nasa.gov) and [`SSHT`](https://github.com/astro-informatics/ssht). This works
187
197
by wrapping Python bindings with custom JAX frontends. Note that this C/C++ to JAX interoperability is currently limited to CPU.
@@ -207,7 +217,6 @@ For further details on usage see the associated [notebooks](https://astro-inform
207
217
208
218
A suite of benchmark functions for both the on-the-fly and precompute versions of the spherical harmonic and Wigner transforms are available in the `benchmarks` directory, along with utilities for running the benchmarks and plotting the results.
209
219
210
-
211
220
## Contributors ✨
212
221
213
222
Thanks goes to these wonderful people ([emoji
@@ -300,13 +309,13 @@ it will be of use to a wider community.
300
309
Copyright 2023 Matthew Price, Jason McEwen and contributors.
301
310
302
311
`S2FFT` is free software made available under the MIT License. For
303
-
details see the [`LICENCE.txt`](LICENCE.txt) file.
312
+
details see the [`LICENCE.txt`](https://github.com/astro-informatics/s2fft/blob/main/LICENCE.txt) file.
304
313
305
-
The file [`lib/include/kernel_helpers.h`](lib/include/kernel_helpers.h) is adapted from
314
+
The file [`lib/include/kernel_helpers.h`](https://github.com/astro-informatics/s2fft/blob/main/lib/include/kernel_helpers.h) is adapted from
306
315
[code](https://github.com/dfm/extending-jax/blob/c33869665236877a2ae281f3f5dbff579e8f5b00/lib/kernel_helpers.h) in [a tutorial on extending JAX](https://github.com/dfm/extending-jax) by
307
316
[Dan Foreman-Mackey](https://github.com/dfm) and licensed under a [MIT license](https://github.com/dfm/extending-jax/blob/371dca93c6405368fa8e71690afd3968d75f4bac/LICENSE).
308
317
309
-
The file [`lib/include/kernel_nanobind_helpers.h`](lib/include/kernel_nanobind_helpers.h)
318
+
The file [`lib/include/kernel_nanobind_helpers.h`](https://github.com/astro-informatics/s2fft/blob/main/lib/include/kernel_nanobind_helpers.h)
310
319
is adapted from [code](https://github.com/jax-ml/jax/blob/3d389a7fb440c412d95a1f70ffb91d58408247d0/jaxlib/kernel_nanobind_helpers.h)
311
320
by the [JAX](https://github.com/jax-ml/jax) authors
312
321
and licensed under a [Apache-2.0 license](https://github.com/jax-ml/jax/blob/3d389a7fb440c412d95a1f70ffb91d58408247d0/LICENSE).
0 commit comments