+
+

+
+# S2FFT: differentiable and accelerated spherical transforms
+
[](https://github.com/astro-informatics/s2fft/actions/workflows/tests.yml)
[](https://github.com/astro-informatics/s2fft/actions/workflows/linting.yml)
[](https://github.com/astro-informatics/s2fft/actions/workflows/docs.yml)
[](https://codecov.io/gh/astro-informatics/s2fft)
[](https://opensource.org/licenses/MIT)
[](https://badge.fury.io/py/s2fft)
-[](https://arxiv.org/abs/2311.14670)
-[](#contributors-)
-
+[](https://arxiv.org/abs/2311.14670)
+
[](https://colab.research.google.com/github/astro-informatics/s2fft/blob/main/notebooks/spherical_harmonic_transform.ipynb)
[](https://github.com/astral-sh/ruff)
-

-
-# Differentiable and accelerated spherical transforms
+
 +
+# S2FFT: differentiable and accelerated spherical transforms
+
[](https://github.com/astro-informatics/s2fft/actions/workflows/tests.yml)
[](https://github.com/astro-informatics/s2fft/actions/workflows/linting.yml)
[](https://github.com/astro-informatics/s2fft/actions/workflows/docs.yml)
[](https://codecov.io/gh/astro-informatics/s2fft)
[](https://opensource.org/licenses/MIT)
[](https://badge.fury.io/py/s2fft)
-[](https://arxiv.org/abs/2311.14670)
-[](#contributors-)
-
+[](https://arxiv.org/abs/2311.14670)
+
[](https://colab.research.google.com/github/astro-informatics/s2fft/blob/main/notebooks/spherical_harmonic_transform.ipynb)
[](https://github.com/astral-sh/ruff)
-
+
+# S2FFT: differentiable and accelerated spherical transforms
+
[](https://github.com/astro-informatics/s2fft/actions/workflows/tests.yml)
[](https://github.com/astro-informatics/s2fft/actions/workflows/linting.yml)
[](https://github.com/astro-informatics/s2fft/actions/workflows/docs.yml)
[](https://codecov.io/gh/astro-informatics/s2fft)
[](https://opensource.org/licenses/MIT)
[](https://badge.fury.io/py/s2fft)
-[](https://arxiv.org/abs/2311.14670)
-[](#contributors-)
-
+[](https://arxiv.org/abs/2311.14670)
+
[](https://colab.research.google.com/github/astro-informatics/s2fft/blob/main/notebooks/spherical_harmonic_transform.ipynb)
[](https://github.com/astral-sh/ruff)
- -
-# Differentiable and accelerated spherical transforms
+
-
-# Differentiable and accelerated spherical transforms
+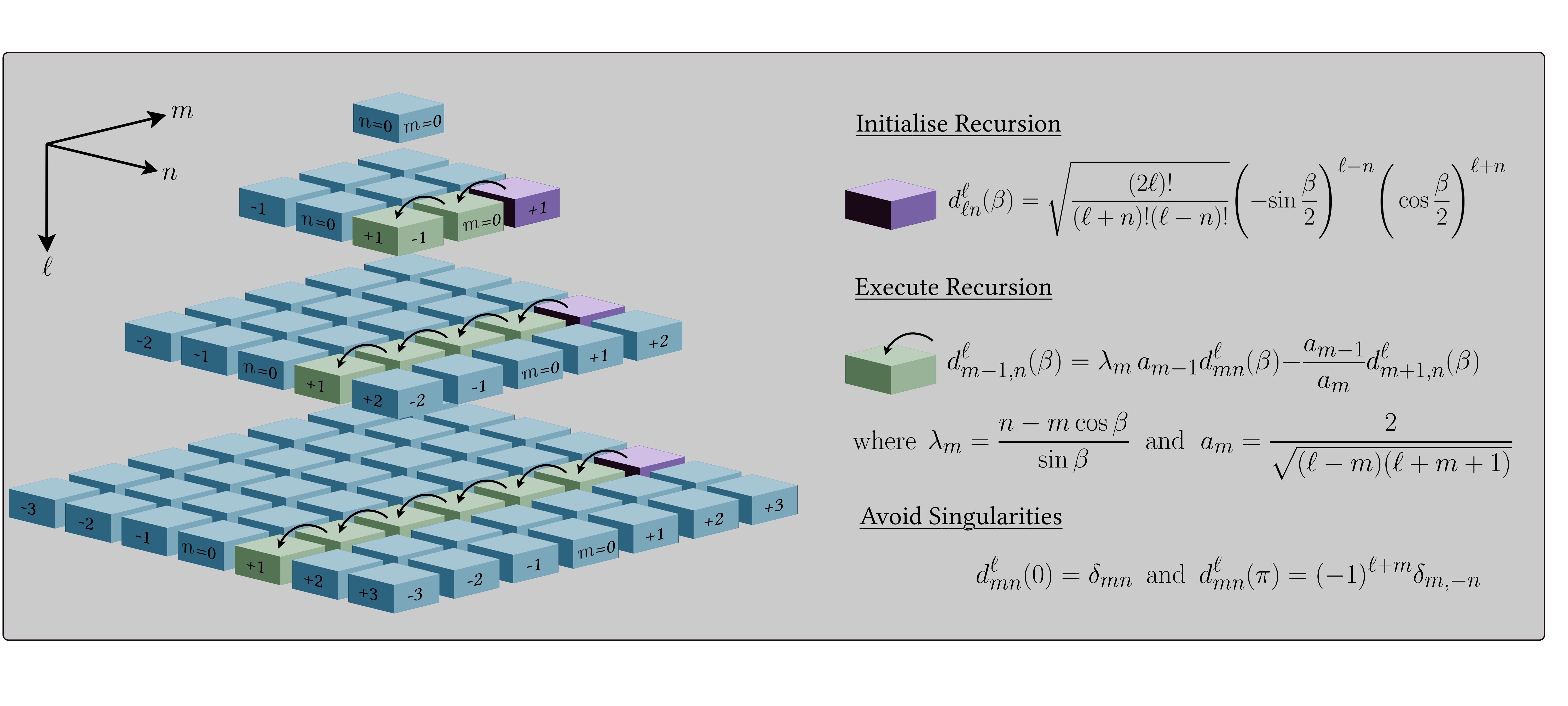 +
+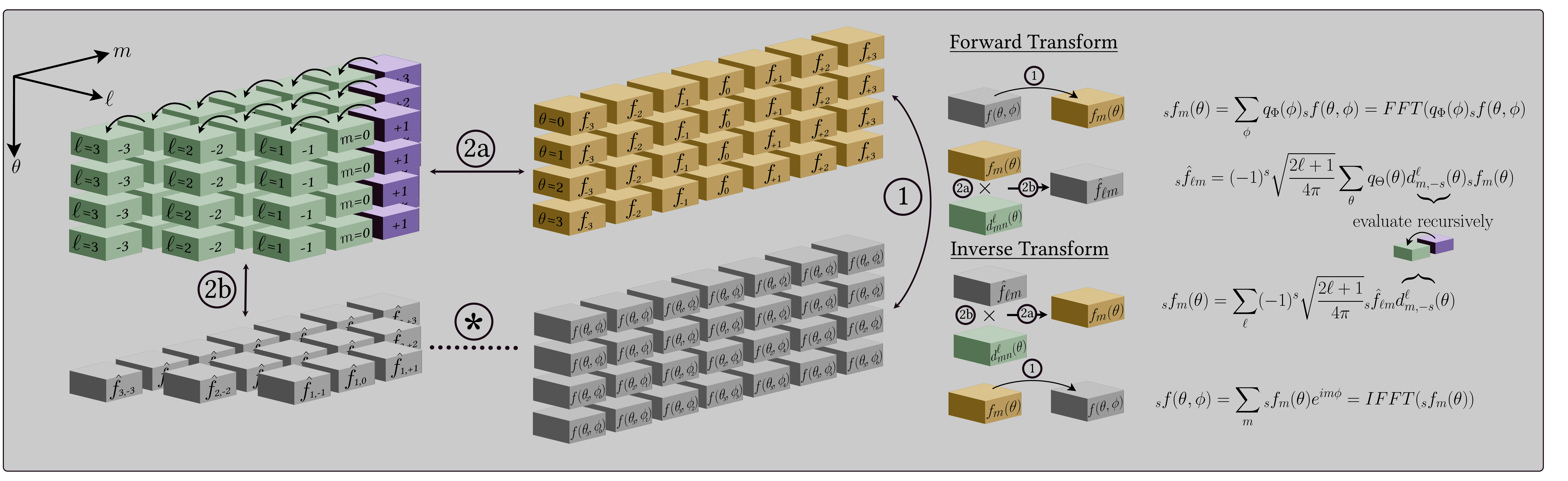 +
+
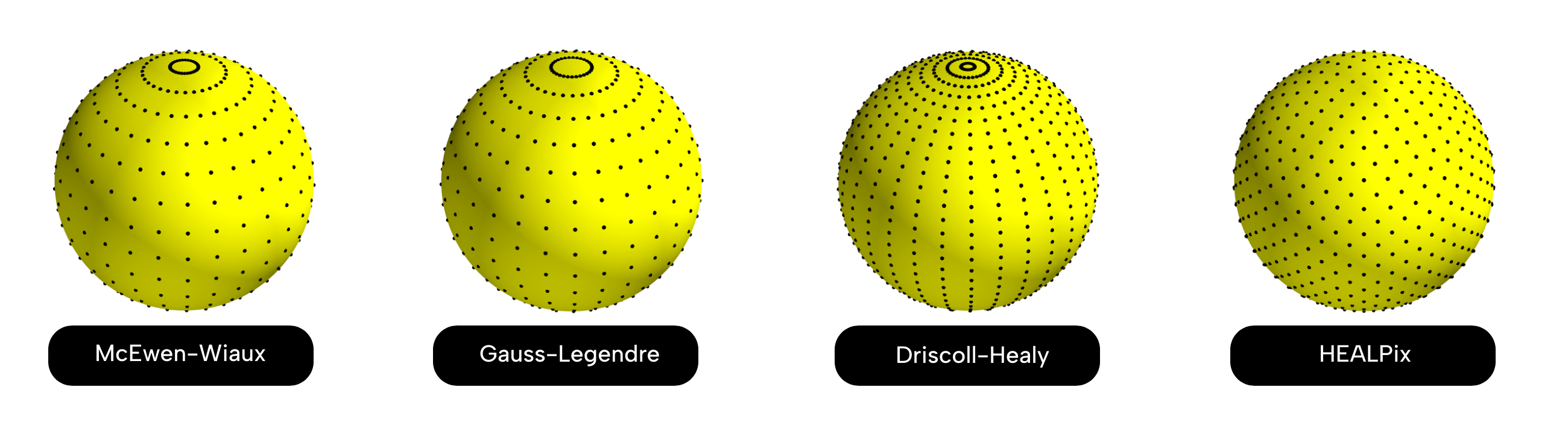 +
+