|
| 1 | +# Graph Theory |
| 2 | + |
| 3 | +## What is a Graph? |
| 4 | + |
| 5 | +A _graph_ consists of _vertices_ (or nodes) and _edges_ (or paths) |
| 6 | + |
| 7 | +Edges |
| 8 | +- are connections between vertices |
| 9 | + - _e.g._, roads between cities |
| 10 | +- can have one-way direction or can be bidirectional |
| 11 | +- can have weights |
| 12 | + - _e.g._, time to travel between two cities |
| 13 | + |
| 14 | +A _directional graph_ has edges that are all directional (_i.e._, if there's an edge from _A_ to _B_, there might not be one from _B_ to _A_) |
| 15 | + |
| 16 | +An _acyclic graph_ contains no cycles (in a directed graph, there's no path starting from some vertex _v_ that will take you back to _v_) |
| 17 | + |
| 18 | +A _weighted graph_ contains edges that hold a numerical value (_e.g._, cost, time, etc.) |
| 19 | + |
| 20 | +### Unweighted, undirected graph |
| 21 | + |
| 22 | + |
| 23 | + |
| 24 | +### Unweighted, directed cyclic graph |
| 25 | + |
| 26 | + |
| 27 | + |
| 28 | +### Unweighted, directed acyclic graph |
| 29 | + |
| 30 | + |
| 31 | + |
| 32 | +### Weighted, undirected graph |
| 33 | + |
| 34 | + |
| 35 | + |
| 36 | +### Complete graph |
| 37 | + |
| 38 | +A _complete graph_ is a graph where each vertex has an edge to all other vertices in the graph |
| 39 | + |
| 40 | + |
| 41 | + |
| 42 | +## Representing a Graph |
| 43 | + |
| 44 | +There are two main ways to represent a graph: |
| 45 | +1. _Adjacency matrix_ |
| 46 | +2. _Adjacency list_ |
| 47 | + |
| 48 | +### Adjacency Matrix |
| 49 | + |
| 50 | +An adjacency matrix uses a 2-dimensional array to represent edges between two vertices |
| 51 | + |
| 52 | +There are many ways to use an adjacency matrix to represent a matrix, but we will look at two variations |
| 53 | + |
| 54 | +#### Connection matrix |
| 55 | + |
| 56 | +```java |
| 57 | +boolean[][] conn = new boolean[ N ][ N ]; |
| 58 | +``` |
| 59 | + |
| 60 | +The matrix `conn` tells us if two vertices are connected |
| 61 | + |
| 62 | +```java |
| 63 | +if ( conn[ i ][ j ] ) |
| 64 | + // there is an edge from vertex i to vertex j |
| 65 | + |
| 66 | +else |
| 67 | + // there is no edge from vertex i to vertex j |
| 68 | +``` |
| 69 | + |
| 70 | +#### Cost matrix |
| 71 | + |
| 72 | +```java |
| 73 | +int[][] cost = new int[ N ][ N ]; |
| 74 | +``` |
| 75 | + |
| 76 | +The matrix `cost` tells us the cost (or edge weight) between two vertices |
| 77 | + |
| 78 | +```java |
| 79 | +cost[ i ][ j ] = 7; // this means it costs 7 units to travel from vertex i to vertex j |
| 80 | +cost[ i ][ j ] = 0; // this usually means there is no edge from vertiex i to vertex j |
| 81 | +``` |
| 82 | + |
| 83 | +#### Pros and Cons |
| 84 | + |
| 85 | +_Pros_ |
| 86 | +- Easy to check if there is an edge between _i_ and _j_ |
| 87 | + - calling `matrix[ i ][ j ]` will tell us if there is a connection |
| 88 | + |
| 89 | +_Cons_ |
| 90 | +- To find all neighbors of vertex _i_, you would need to check the value of `matrix[ i ][ j ]` for all _j_ |
| 91 | +- Need to construct a 2-dimensional array of size _N_ x _N_ |
| 92 | + |
| 93 | +### Adjacency List |
| 94 | + |
| 95 | +Rather than making space for all _N_ x _N_ possible edge connections, an _adjacency list_ keeps track of the vertices that a vertex has an edge to. |
| 96 | + |
| 97 | +We are able to do this by creating an `ArrayList` that contains `ArrayLists` holding the values of the vertices that a vertex is connected to. |
| 98 | + |
| 99 | +```java |
| 100 | +ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>(); |
| 101 | + |
| 102 | +// For each vertex, we need to initialize the list of vertices the vertex has a connection to |
| 103 | +for ( int i = 0; i <= N; i++ ) |
| 104 | +{ |
| 105 | + graph.add( new ArrayList<Integer>() ); |
| 106 | +} |
| 107 | + |
| 108 | +graph.get( i ).add( j ); // get the list of vertices for vertex i and add a connection to vertex j |
| 109 | + |
| 110 | +ArrayList<Integer> neighbors = graph.get( k ); // get the list of vertices that vertex k is connected to |
| 111 | +``` |
| 112 | + |
| 113 | +#### Pros and Cons |
| 114 | + |
| 115 | +_Pros_ |
| 116 | +- Saves memory by only keeping track of edges that a vertex has |
| 117 | +- Efficient to iterate over the edges of a vertex |
| 118 | + - Doesn't need to go through all _N_ vertices and check if there is a connection |
| 119 | + |
| 120 | +_Cons_ |
| 121 | +- Difficult to quickly determine if there is an edge between two vertices |
| 122 | + |
| 123 | +## Breadth-first Search |
| 124 | + |
| 125 | +_Breadth-first search_ (or BFS) is a form of graph traversal that starts at some vertex _i_ and visits all of _i_'s neighbors. It then visits all of the neighbors of _i_'s neighbors. This process keeps going until there are no more vertices left to visit. |
| 126 | + |
| 127 | +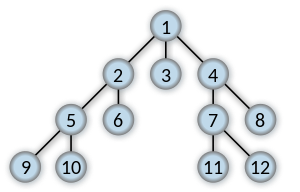 |
| 128 | + |
| 129 | +Imagine a "family tree", like one shown in the picture above. BFS will visit all vertices of the same level before moving on to the next level. |
| 130 | + |
| 131 | +We start by visiting vertex 1. |
| 132 | + |
| 133 | +Then, we visit all of 1's neighbors: 2, 3, 4 |
| 134 | + |
| 135 | +Then, we visit all of 1's neighbors' neighbors: 5, 6, 7, 8 |
| 136 | + |
| 137 | +Finally, we visit all of their neighbors: 9, 10, 11, 12 |
| 138 | + |
| 139 | +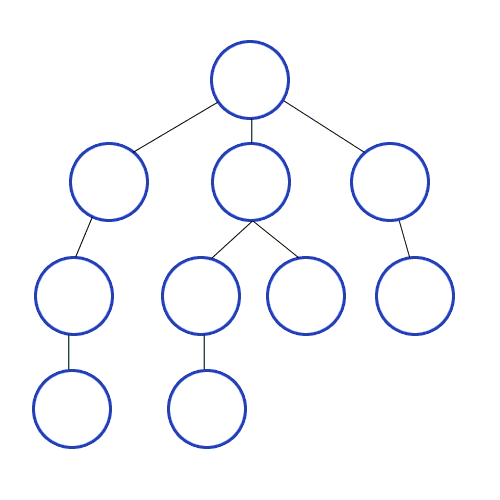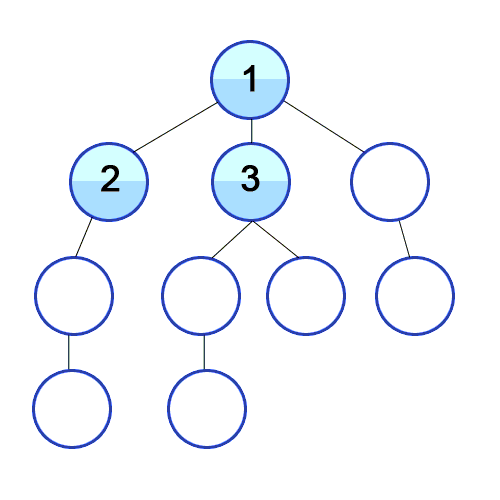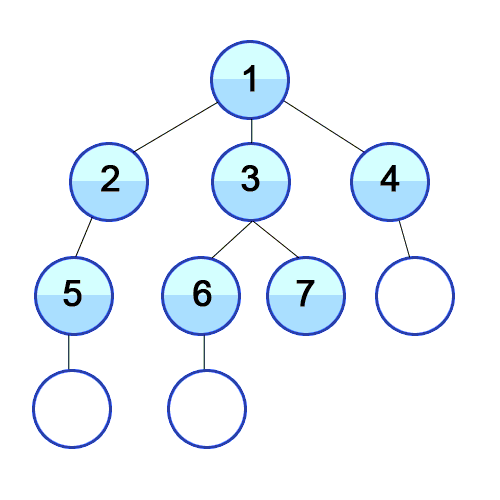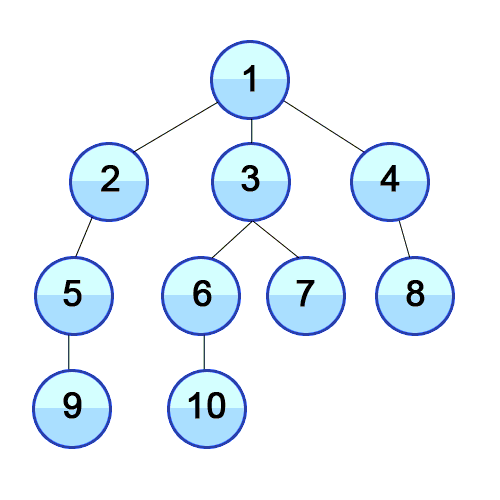 |
| 140 | + |
| 141 | +Above is another visual representation of the BFS process starting from the top vertex. |
| 142 | + |
| 143 | +### Coding BFS |
| 144 | + |
| 145 | +We need to use some data structure that will allow us to visit vertices "_level-by-level_", that is, visit every vertex at level _j_ before we visit any vertex at level _j_+1. |
| 146 | + |
| 147 | +In order to do this, we will be using a `Queue` since it follows the "_first in, first out_" ordering; this means if we put all the vertices at level _j_ into the queue before the vertices at level _j_+1, we are guaranteed to visit the lower level vertices first. |
| 148 | + |
| 149 | + Below are the steps to follow for BFS: |
| 150 | + 1. Push the root vertex onto the queue |
| 151 | + 2. Pop the queue to get the current vertex |
| 152 | + 3. For each unvisited neighbor of the current vertex, mark them as visited and push them onto the queue |
| 153 | + 4. Go back to step 2 until the queue is empty |
| 154 | + |
| 155 | + ```java |
| 156 | + // Initialize the queue |
| 157 | + Queue<Integer> queue = new LinkedList<Integer>(); |
| 158 | + |
| 159 | + // This array will tell us if we have visited a vertex |
| 160 | + boolean[] visited = new boolean[ N ]; |
| 161 | + |
| 162 | + // Push the root vertex onto the queue |
| 163 | + queue.add( rootVertex ); |
| 164 | + |
| 165 | + // While there is a vertex still in the queue... |
| 166 | + while ( !queue.isEmpty() ) |
| 167 | + { |
| 168 | + // Get the current vertex |
| 169 | + Integer current = queue.remove(); |
| 170 | + // Get the current vertex's neighbors |
| 171 | + List<Integer> neighbors = graph.get( current ); |
| 172 | + |
| 173 | + // For each of the current vertex's neighbors... |
| 174 | + foreach ( Integer neighbor : neighbors ) |
| 175 | + { |
| 176 | + // If we haven't visited the neighbor... |
| 177 | + if ( !visited[ neighbor ] ) |
| 178 | + { |
| 179 | + // Add the neighbor to the queue |
| 180 | + queue.add( neighbor ); |
| 181 | + // Mark the neighbor as visited |
| 182 | + visited[ neighbor ] = true; |
| 183 | + } |
| 184 | + } |
| 185 | + } |
| 186 | + ``` |
0 commit comments