|
| 1 | +# Dynamic Programming |
| 2 | + |
| 3 | +## What is Dynamic Programming? |
| 4 | + |
| 5 | +Calculate the answer to the following expression: 3<sup>4</sup> + 5! + (50 * 9) |
| 6 | + |
| 7 | +Now calculate the answer to the following expression: 3<sup>4</sup> + 5! + (50 * 9) + 17 |
| 8 | + |
| 9 | +It was much easier to calculate the second expression than it was the first, but why? |
| 10 | + |
| 11 | +You didn't need to recalculate the entire second expression because you _memorized_ the value of the first expression and used it for a later time. |
| 12 | + |
| 13 | +That's exactly what dynamic programming is: _remembering information in order to save some time later on_. |
| 14 | + |
| 15 | +## What is Dynamic Programming (Mathematical definition) |
| 16 | + |
| 17 | +Dynamic programming is a method for solving complex problems by breaking it down into a collection of simpler subproblems. |
| 18 | + |
| 19 | +Dynamic programming problems exhibit two properties: |
| 20 | +- Overlapping subproblems |
| 21 | +- Optimal substructure |
| 22 | + |
| 23 | +So what exactly does this mean? Let's take a look at some examples. |
| 24 | + |
| 25 | +## Fibonacci Sequence |
| 26 | + |
| 27 | +The Fibonacci sequence is one in which a term in the sequence is determined by the sum of the two terms before it. |
| 28 | + |
| 29 | +1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... |
| 30 | + |
| 31 | +We say that the _n_<sup>_th_</sup> Fibonacci number can be found by F<sub>n</sub> = F<sub>n-1</sub> + F<sub>n-2</sub>, where F<sub>0</sub> = 1 and F<sub>1</sub> = 1 |
| 32 | + |
| 33 | +Let's say we wanted to write a recursive function for this sequence to determine the n<sup>th</sup> Fibonacci number. |
| 34 | + |
| 35 | +```java |
| 36 | +// This function will return the nth Fibonacci number |
| 37 | +public int fib( int n ) |
| 38 | +{ |
| 39 | + // Base case: the first two Fibonacci numbers are 1 |
| 40 | + if ( n == 0 || n == 1 ) |
| 41 | + return 1; |
| 42 | + return fib( n - 1 ) + fib( n - 2 ); |
| 43 | +} |
| 44 | +``` |
| 45 | + |
| 46 | +What will be the function calls if we wanted to determine `fib( 5 )`? |
| 47 | + |
| 48 | +``` |
| 49 | +fib( 5 ) |
| 50 | +fib( 4 ) + fib( 3 ) |
| 51 | +fib( 3 ) + fib( 2 ) + fib( 3 ) |
| 52 | +fib( 2 ) + fib( 1 ) + fib( 2 ) + fib( 3 ) |
| 53 | +fib( 1 ) + fib( 0 ) + 1 + fib( 2 ) + fib( 3 ) |
| 54 | +1 + 1 + 1 + fib( 2 ) + fib( 3 ) |
| 55 | +``` |
| 56 | + |
| 57 | +Is it necessary to compute `fib( 2 )` and `fib( 3 )`? |
| 58 | + |
| 59 | +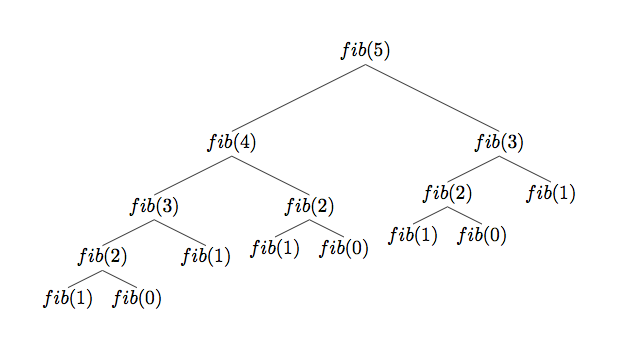 |
| 60 | + |
| 61 | +The above tree represents the function calls for `fib( 5 )` |
| 62 | + |
| 63 | +Notice that when we calculate `fib( 4 )` we also calculate the value of `fib( 3 )` |
| 64 | + |
| 65 | +When we call `fib( 5 )`, it calls `fib( 3 )`, but if we already have the value of that function call from before, there's no need to recompute it. |
| 66 | + |
| 67 | +Since `fib( 5 )` asks us to call the function `fib( 3 )` _multiple times_, we have found an _overlapping subproblem_ - a subproblem that is reused numerous times, but given the same result each time it's solved. |
| 68 | + |
| 69 | +`fib( 3 )` will give us the same result no matter how many times we call it. |
| 70 | + |
| 71 | +Rather than solving these overlapping subproblems _every time_, we can do the following: |
| 72 | +- solve the subproblem once and save its value |
| 73 | +- when you need to solve the subproblem _again_, rather than going through all the computation to do the solving, return the _memorized_ value |
| 74 | + |
| 75 | +```java |
| 76 | +int[] dp = new int[ SIZE ]; // all values initialized to 0 |
| 77 | +public int fib( int n ) |
| 78 | +{ |
| 79 | + if ( n == 0 || n == 1 ) |
| 80 | + return 1; |
| 81 | + if ( dp[ n ] != 0 ) |
| 82 | + return dp[ n ]; |
| 83 | + return dp[ n ] = fib( n - 1 ) + fib( n - 2 ); |
| 84 | +} |
| 85 | +``` |
| 86 | + |
| 87 | +## Pascal's Triangle |
| 88 | + |
| 89 | +In mathematics, Pascal's triangle is a triangular array of the binomial coefficients. |
| 90 | + |
| 91 | +Binomial coefficients can be read as "_n_ choose _k_" - how many ways are there to choose _k_ elements from a set of _n_ elements? |
| 92 | + |
| 93 | +The entries in each row are numbered with row _n_ = 0 at the top, and the entries in each row are numbered from the left beginning with _k_ = 0 |
| 94 | + |
| 95 | +The _k_<sup>_th_</sup> element in the _n_<sup>_th_</sup> row represents "_n_ choose _k_" |
| 96 | + |
| 97 | + |
| 98 | + |
| 99 | +Elements in each row of Pascal's triangle can be found by summing the two numbers in the row above and to the left and right of the element. |
| 100 | + |
| 101 | +This property can be seen as a closed formula: |
| 102 | + |
| 103 | + |
| 104 | + |
| 105 | +Let's try and create a recursive method that will find us "_n_ choose _k_" using the above formula. |
| 106 | + |
| 107 | +What are the base cases? |
| 108 | + |
| 109 | +We know that there is only _one_ way to choose zero elements from an _n_-element set, as well as _one_way to choose _n_ elements from an _n_-element set. |
| 110 | + |
| 111 | +```java |
| 112 | +// This function will return "n choose k" |
| 113 | +public int pascal( int n, int k ) |
| 114 | +{ |
| 115 | + if ( k == 0 || k == n ) |
| 116 | + return 1; |
| 117 | + return pascal( n - 1, k - 1 ) + pascal( n - 1, k ); |
| 118 | +} |
| 119 | +``` |
| 120 | + |
| 121 | +This function leaves us with the same problem we hads with the Fibonacci function: we are going to be recalculating subproblems that we have already solved before. |
| 122 | + |
| 123 | +We can fix this like we did with the Fibonacci function: memorizing the value of the subproblems so that we don't have to recalculate them later. |
| 124 | + |
| 125 | +```java |
| 126 | +int[][] dp = new int[ N_SIZE ][ K_SIZE ]; |
| 127 | +public int pascal( int n, int k ) |
| 128 | +{ |
| 129 | + if ( k == 0 || k == n ) |
| 130 | + return 1; |
| 131 | + if ( dp[ n ][ k ] != 0 ) |
| 132 | + return dp[ n ][ k ]; |
| 133 | + return dp[ n ][ k ] = pascal( n - 1, k - 1 ) + pascal ( n - 1, k ); |
| 134 | +} |
| 135 | +``` |
| 136 | + |
| 137 | +## Knapsack Problem |
0 commit comments