11. 盛最多水的容器

[crawler-django]

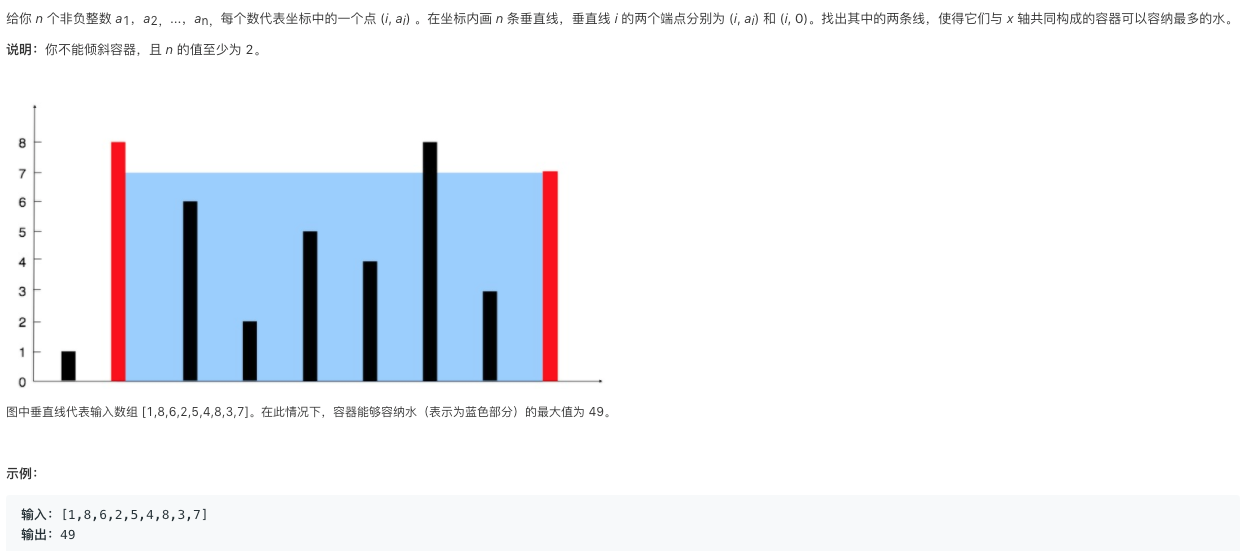
题目描述: 给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

问题1: 怎么找区域面积的最大值? 好像没什么规律可言, 得一个个计算来找?
答: 是的... 真的得一个个计算来找, 最优解可以排除大量的计算. 我觉得的最优解是双指针法, 当时我是想用动态规划做的, 因为最近对动态规划有了更深的理解, 所以我当时的第一想法就是用动态规划.....(此题用动态规划复杂度太高, �过不了时间限制, 下面只是记录一下动态规划的想法)

当时我列出来的动态规划是这么算的... 就像图中x坐标从1到9, 假设x -> (1,9)里的最大区域面积为maxArea(1, 9). 假设x ---> (1, 9)的面积为Area(1, 9) (一个是最大的区域面积, 一个是(min(y1, y9) * 8 ). 然后我就列了一个式子.

        maxArea(1, 9) =  Area(1, 9) > maxArea(1, 8) ? 
                                         (Area(1, 9) > maxArea(2, 9) ? Area(1, 9) : maxArea(2, 9)) 
                                         : maxArea(1, 8)
    // 然后同理...maxArea(1, 8), maxArea(2, 9) 一直往下算, 然后值存起来.

按这个方法写下来, 是可以解出来的, 但是写的过程中比较复杂, 而且效率不高, 整体都远远不如另一种方法(双指针法), 动态规划在这道题中复杂度太高.

接下来讲讲双指针法.

双指针法:

问题1: 双指针法是怎样的? 怎么使用?
答:
所谓双指针, 指的是在遍历对象的过程中, 不是普通的使用单个指针进行访问, 而是使用两个相同方向或者相反方向的指针进行扫描, 从而达到相应的目的.

这道题的双指针使用方法 就是边界左右各设一个指针如left, right. 假设y值的数组为heights. 那么从left开始到right结束, 这个区域的大小就为 min( heights[left], height[right] ) * (right - left). 因为区域面积的大小是由它们短板决定的. 所以我们指针移动的时候, 总是移动最短的那一边。 为什么呢?

就是因为区域面积的大小是由它们短板决定的, 因为y值只能取最小, 如果移动长的那一版, y值要么跟原来一样, 要么比原来更小, 而x是越来越小的, 那么x * y只能越来越小, 不能算出最大的区域面积. 只有移动最短的那一边, 才能得到可能的更大的值.

所以我们总是移动最短的那一边, 如果两边一样, 就随便选一边, 直到left = right, 结束循环.

代码如下:

var maxArea = function(height) {
    let len = height.length

    let max = 0

    let left = 0
    let right = len - 1

    while(left !== right) {
        let tempArea = 0
        if (height[left] < height[right]) {
            tempArea = height[left] * (right - left)
            left += 1
        } else {
            tempArea = height[right] * (right - left)
            right -= 1
        }

        if (tempArea > max) {
            max = tempArea
        }
    }

    return max
};

运行结果: