diff --git a/source/_posts/LibRI.md b/source/_posts/LibRI.md
new file mode 100644
index 00000000..15be6b9d
--- /dev/null
+++ b/source/_posts/LibRI.md
@@ -0,0 +1,94 @@
+---
+title: "LibRI | Collaborating with the DeepModeling Community to Support Advanced Methods Beyond Conventional DFT"
+date: 2023-05-26
+categories:
+- LibRI
+mathjax: true
+---
+
+## Introducing LibRI: Advancing Computational Methods for DFT
+
+### Development and Features
+
+**Dr. Peize Lin** and the research group led by **Xinguo Ren** at the Institute of Physics, Chinese Academy of Sciences, have developed the open-source library **LibRI**. This innovative tool is designed for **high-efficiency and highly parallelized RI model calculations** and has already integrated several advanced electronic structure computation methods.
+
+### Joining the DeepModeling Community
+
+To accelerate its development and broaden its impact, **LibRI has joined the DeepModeling community**. This collaboration will:
+- Support **advanced methods that go beyond conventional DFT**, enabling the further development of RI methods.
+- Provide **more efficient and accurate computational capabilities** for the domestic DFT software **ABACUS**, boosting its performance and efficiency.
+- Contribute to **AI-assisted, next-generation electronic structure algorithms**.
+
+
+
+
+### The Importance of Density Functional Theory
+
+**Density Functional Theory (DFT)** is a cornerstone in first-principles electronic structure calculations. Recent advances in **accuracy** and **speed** have made DFT a widely used tool in fields such as:
+- **Physics**
+- **Materials Science**
+- **Chemistry**
+- **Biology**
+
+However, DFT methods based on local or semi-local exchange-correlation functional approximations face significant limitations. These functionals rely solely on charge density and its gradient, which prevents accurate descriptions of certain critical physical interactions.
+
+### Overcoming Limitations with Advanced Methods
+
+To address these limitations, higher-level methods, such as:
+- **Hybrid Density Functionals**
+- **Random Phase Approximation (RPA)**
+- **GW Methods**
+
+are often required for more accurate calculations, such as ground-state energies or quasiparticle excitation energies. Unfortunately, these methods are computationally intensive, with costs scaling **quartically with system size**, restricting their use for large systems.
+
+### The Role of the RI Method in LibRI
+
+The **Resolution of Identity (RI)** method reduces computational cost by expanding localized orbital products onto a selected auxiliary basis set, significantly lowering computational scaling. This allows advanced methods to be applied to large systems.
+
+The research group developed a **unified mathematical model** for the RI method, enabling various advanced methods to share the same computational framework. This abstraction means developers can focus on **physical problems** without worrying about code optimization, reducing development complexity for both computation and method development.
+
+### Optimization and Applications
+
+LibRI incorporates a series of optimized algorithms to enhance computational speed and **parallel algorithms** for efficient resource use, enabling large-scale, high-level calculations on systems with thousands of atoms. It has already been integrated into **ABACUS**, supporting self-consistent electronic structure calculations, structural relaxation, and molecular dynamics simulations for hybrid functionals. Development of **low-scaling RPA** and **\(G_0W_0\)** functionalities is nearly complete, with internal testing underway.
+
+### Acknowledgments
+
+The development of LibRI received support from:
+- **Prof. Lixin He (USTC)**
+- **Profs. Hongming Weng and Sheng Meng (Institute of Physics)**
+- **Prof. Mohan Chen (Peking University)**
+
+Contributions were also made by:
+- **Minye Zhang (Institute of Physics)**
+- **Rong Shi (USTC)**
+- **Yuyang Ji (USTC)**
+- **Xinyang Dong (Beijing Academy of Artificial Intelligence, AISI)**
+- **Wenfei Li (AISI)**
+- **Qi Ou (AISI)**
+- **Yu Cao (Peking University)**
+
+Special thanks to the **DeepModeling community** for offering comprehensive support and providing a broader platform for model reuse and sharing.
+
+### Further Development
+LibRI will focus on three key areas of future development:
+
+1. **Deeper Optimization of RI Model Computations**
+ Efforts will continue to further optimize RI model computations, enabling the handling of larger systems and enhancing the degree of parallelism.
+
+2. **Expanding High-Level Methods Compatible with the RI Model**
+ Additional advanced electronic structure calculation methods will be developed, with an emphasis on achieving greater precision and efficiency.
+
+3. **Collaboration with DFT Software Using Localized Orbitals**
+ Partnerships will be established with DFT software based on localized orbitals, allowing more DFT programs to perform large-scale high-level method calculations.
+
+### Project Repository
+
+LibRI has now joined the DeepModeling community. The project repository is available at:
+[https://github.com/deepmodeling/LibRI.git](https://github.com/deepmodeling/LibRI.git)
+(The original repository was located at: [https://github.com/abacusmodeling/LibRI.git](https://github.com/abacusmodeling/LibRI.git))
+
+#### How to Contribute
+
+We welcome everyone to participate by creating issues and submitting pull requests in the LibRI GitHub repository. Additionally, we encourage users performing electronic structure calculations to provide feedback and share their needs and challenges in materials computations. These valuable suggestions will help refine and improve LibRI further.
+
+
diff --git a/source/_posts/ReacNetGenerator.md b/source/_posts/ReacNetGenerator.md
new file mode 100644
index 00000000..80e03852
--- /dev/null
+++ b/source/_posts/ReacNetGenerator.md
@@ -0,0 +1,83 @@
+---
+title: "ReacNetGenerator | Partnering with the DeepModeling Community to Advance Research on Complex Reaction Systems"
+date: 2024-09-01
+categories:
+- ReacNetGenerator
+mathjax: true
+---
+
+The **ReacNetGenerator** project has officially joined the **DeepModeling** open-source community, aiming to further advance its development.
+
+### Project Homepage
+[https://github.com/deepmodeling/reacnetgenerator](https://github.com/deepmodeling/reacnetgenerator)
+
+
+
+### Background
+
+In recent years, **reactive molecular dynamics (Reactive MD)** simulation methods have been widely used to study the reaction mechanisms of various complex molecular systems, such as:
+- **Combustion**
+- **Explosions**
+- **Heterogeneous catalysis**
+
+However, long-term MD simulations of large systems generate highly complex trajectory files that include numerous reactions and molecular species. **Manually analyzing such trajectories is impractical.**
+
+---
+
+### About ReacNetGenerator
+
+To address these challenges, the **ReacNetGenerator** software was introduced in the spring of 2018.
+
+#### Key Features:
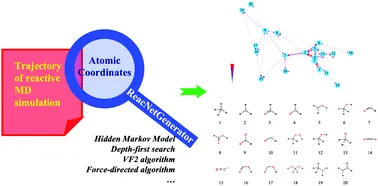
+- **Input Requirements:** Uses atomic coordinates from the trajectory as its sole input.
+- **Automatic Analysis:** Determines species and reactions based on atomic connectivity.
+- **Interactive Visualization:** Presents reaction types, quantities, and networks on an interactive webpage.
+ - Users can click to analyze localized reaction networks involving specific species.
+- **Noise Filtering:** Employs a **Hidden Markov Model (HMM)** to filter noise, highlighting key reactions.
+- **High Efficiency:** Supports **parallel computing** and optimized memory usage, making it capable of analyzing large trajectory files.
+
+ +
+
+---
+
+
+**Original Paper:**
+Jinzhe Zeng, Liqun Cao, Chih-Hao Chin, Haisheng Ren, John Z. H. Zhang, Tong Zhu,
+*ReacNetGenerator: an automatic reaction network generator for reactive molecular dynamics simulations*,
+**Phys. Chem. Chem. Phys.**, 2020, 22 (2), 683–691.
+[https://doi.org/10.1039/C9CP05091D](https://doi.org/10.1039/C9CP05091D)
+
+Check out following publications employing **ReacNetGenerator** in their research: https://blogs.deepmodeling.com/papers/ReacNetGenerator/
+
+---
+
+### Impact
+
+By joining the **DeepModeling community**, ReacNetGenerator aims to further facilitate research on complex reaction systems, advancing our understanding of intricate molecular dynamics.
+
+
+### Installation and Usage of ReacNetGenerator
+
+You can install **ReacNetGenerator** using either `pip` or `conda`:
+
+#### Using `pip`:
+```bash
+pip install reacnetgenerator
+```
+
+#### Using `conda`:
+```bash
+conda install reacnetgenerator -c conda-forge
+```
+
+**Verify Installation**
+
+After installation, you can check if **ReacNetGenerator** was installed successfully by running:
+```bash
+reacnetgenerator -h
+```
+
+If installed correctly, this will display the help information and available commands for the software.
+
+
diff --git a/source/_posts/TBPLaS.md b/source/_posts/TBPLaS.md
new file mode 100644
index 00000000..aea8860f
--- /dev/null
+++ b/source/_posts/TBPLaS.md
@@ -0,0 +1,267 @@
+---
+title: "TBPLaS | Partnering with the DeepModeling Community to Build Large-Scale Computational Physics Software"
+date: 2024-03-15
+categories:
+- TBPLaS
+mathjax: true
+---
+
+The **tight-binding model** based on **second quantization** is a widely used theoretical model in **condensed matter physics**. In this model:
+
+- Atoms in a lattice are represented as **discrete points** with a specific number of electrons.
+- Each electron occupies a corresponding **atomic orbital**.
+- Using **creation and annihilation operators**, electron transitions between atomic orbitals are described in the second quantization framework.
+- The **Hamiltonian** comprises:
+ - **Transition terms** between atomic orbitals.
+ - **Energy levels** of the orbitals.
+
+Project on GitHub: https://github.com/deepmodeling/tbplas
+
+
+
+
+---
+
+
+**Original Paper:**
+Jinzhe Zeng, Liqun Cao, Chih-Hao Chin, Haisheng Ren, John Z. H. Zhang, Tong Zhu,
+*ReacNetGenerator: an automatic reaction network generator for reactive molecular dynamics simulations*,
+**Phys. Chem. Chem. Phys.**, 2020, 22 (2), 683–691.
+[https://doi.org/10.1039/C9CP05091D](https://doi.org/10.1039/C9CP05091D)
+
+Check out following publications employing **ReacNetGenerator** in their research: https://blogs.deepmodeling.com/papers/ReacNetGenerator/
+
+---
+
+### Impact
+
+By joining the **DeepModeling community**, ReacNetGenerator aims to further facilitate research on complex reaction systems, advancing our understanding of intricate molecular dynamics.
+
+
+### Installation and Usage of ReacNetGenerator
+
+You can install **ReacNetGenerator** using either `pip` or `conda`:
+
+#### Using `pip`:
+```bash
+pip install reacnetgenerator
+```
+
+#### Using `conda`:
+```bash
+conda install reacnetgenerator -c conda-forge
+```
+
+**Verify Installation**
+
+After installation, you can check if **ReacNetGenerator** was installed successfully by running:
+```bash
+reacnetgenerator -h
+```
+
+If installed correctly, this will display the help information and available commands for the software.
+
+
diff --git a/source/_posts/TBPLaS.md b/source/_posts/TBPLaS.md
new file mode 100644
index 00000000..aea8860f
--- /dev/null
+++ b/source/_posts/TBPLaS.md
@@ -0,0 +1,267 @@
+---
+title: "TBPLaS | Partnering with the DeepModeling Community to Build Large-Scale Computational Physics Software"
+date: 2024-03-15
+categories:
+- TBPLaS
+mathjax: true
+---
+
+The **tight-binding model** based on **second quantization** is a widely used theoretical model in **condensed matter physics**. In this model:
+
+- Atoms in a lattice are represented as **discrete points** with a specific number of electrons.
+- Each electron occupies a corresponding **atomic orbital**.
+- Using **creation and annihilation operators**, electron transitions between atomic orbitals are described in the second quantization framework.
+- The **Hamiltonian** comprises:
+ - **Transition terms** between atomic orbitals.
+ - **Energy levels** of the orbitals.
+
+Project on GitHub: https://github.com/deepmodeling/tbplas
+
+ +
+
+
+
+**Challenges in Large-Scale Computation**
+Solving the tight-binding model typically involves:
+- The **stationary Schrödinger equation**, requiring diagonalization of the Hamiltonian.
+- A computational complexity proportional to the **cube of the system size** (\(O(N^3)\)).
+
+For instance:
+- In a **3D system**, if the size increases tenfold:
+ - The **volume** and **number of atoms** increase by **1,000 times**.
+ - The Hamiltonian's **dimension** grows 1,000-fold.
+ - The time required for diagonalization increases nearly **1 billion times**.
+
+This poses significant challenges for **large-scale numerical computations** in fields such as:
+- Defects, impurities, and interfaces.
+- Superlattices, alloys, and clusters.
+- Quasicrystals, fractals, polycrystals, and amorphous systems.
+
+**Breakthrough with TBPLaS**
+Addressing these challenges, **Professor Shengjun Yuan** from **Wuhan University** has:
+- Conducted **over a decade of research** to propose universally applicable computational physics formulas.
+- Developed the **Tight-Binding Propagation Method (TBPM)** and the **TBPLaS** software package.
+
+**Key Features of TBPLaS**
+- **Low-scaling computation**: Overcomes the limitations of traditional diagonalization methods.
+- **Scalable simulations**: Can simulate systems spanning nearly **10 orders of magnitude** in size, including those with billions of atoms (lattice points).
+
+**Collaboration with DeepModeling**
+TBPLaS has officially joined the **DeepModeling community** to:
+- Collaborate with developers and users.
+- Promote the development and application of **large-scale computational physics methods** and **software**.
+
+---
+
+## Basics
+The core idea of the TBPM (Tight-Binding Propagation Method) is as follows: In solid-state physics, a random state in real space contains information about all eigenstates of the system. As the wave function of the random state evolves, each eigenstate evolves independently. However, in terms of physical observables, what is needed is the contribution from a group of eigenstates with similar eigenvalues, not their individual characteristics. Hence, this idea suggests that information from the wave function’s time-domain evolution can be converted into physical quantities of interest, thereby avoiding the diagonalization process. By reducing the computational complexity from \(O(N^3)\) to \(O(N)\), this approach ensures that the linear scaling relationship between computational cost and system size is maintained, even for extremely large systems.
+
+Below is a brief explanation using electronic transport properties as an example. The formula for the electrical conductivity \(\sigma_{AA}(E, \tau)\) is approximately:
+
+\[
+\sigma_{AA}(E, \tau) \approx \frac{1}{\Omega} \rho(E) \int_0^{\tau} dt \, \text{Re} \left[ e^{-iEt} \langle \phi | A e^{iHt} J_A e^{-iHt} | \phi \rangle \right]
+\]
+
+Here:
+- \(|\phi\rangle\) represents a random initial state.
+- \(|\phi(t)\rangle\) is the time-evolved state calculated from \(|\phi\rangle\) (via the time-dependent Schrödinger equation).
+- \(\Omega\) is the system's volume (or area in 2D).
+- \(J_A\) is the \(A\)-direction component of the current operator.
+- \(\rho(E)\) is the electronic density of states (which can be obtained via the spectral correlation function).
+- The time-evolution operator \(e^{iHt}\) is computed using the Chebyshev polynomial expansion method.
+
+The quantity \(\sigma_{AA}(E, \tau)\) is determined by the integral up to the time limit \(\tau\). It provides information about the energy-dependent conductivity, with \(\rho(E)\) describing the contribution of states near energy \(E\). The diffusion coefficient \(D_{AA}(E, \tau)\), derived from this method, captures the dynamics and transport properties over different timescales. Additionally, quantities like the mean free path and localization length can be obtained.
+
+For more computational details, refer to the following articles:
+- *Phys. Rev. B 82, 115448 (2010)* (Electrical, optical, and transport properties)
+- *Phys. Rev. B 84, 035439 (2011)* (Polarization and related quantities)
+- *Phys. Rev. B 91, 045420 (2015)* (Transport properties)
+- *Comput. Phys. Commun. 285, 108632 (2023)* (Summary of the computational methodology for transport properties)
+- *Chin. Phys. Lett. 40, 027101 (2023)* (Automated self-consistent calculations of the electronic density distribution).
+
+---
+## **Features of TBPLaS**
+
+
+**1. Powerful Modeling Capabilities**
+- **Supports diverse models**:
+ - Tight-binding models in arbitrary dimensions, shapes, and boundary conditions.
+ - Molecules, clusters, nanotubes, nanoribbons, 2D crystals, 3D crystals, etc.
+- **Built-in modeling tools**:
+ - Quickly construct complex models like heterojunctions, twisted structures, quasicrystals, and fractals.
+ - Handle defects like vacancies and deformations, as well as external electric and magnetic fields.
+- **Analytical support**:
+ - Derive and use analytical Hamiltonians directly.
+- **Built-in formula libraries**:
+ - **Slater-Koster formula library**: Build tight-binding models directly from atomic structures.
+ - **Spin-orbit coupling formula library**: Support various spin-orbit coupling effects.
+- **Predefined material models**:
+ - Tight-binding models for common materials like graphene, phosphorene, and transition metal dichalcogenides are readily available.
+- **Parameter optimization**:
+ - Fit tight-binding models to band structures obtained from first-principles calculations.
+- **Seamless integration**:
+ - Interface with **Wannier90**: Directly import tight-binding models fitted by Wannier90.
+ - Interface with **LAMMPS**: Import optimized atomic configurations to build tight-binding models.
+ - Interface with **DeePTB** and **DeepH**: Directly import machine-learning-fitted tight-binding models.
+
+
+
+
+
+
+**Challenges in Large-Scale Computation**
+Solving the tight-binding model typically involves:
+- The **stationary Schrödinger equation**, requiring diagonalization of the Hamiltonian.
+- A computational complexity proportional to the **cube of the system size** (\(O(N^3)\)).
+
+For instance:
+- In a **3D system**, if the size increases tenfold:
+ - The **volume** and **number of atoms** increase by **1,000 times**.
+ - The Hamiltonian's **dimension** grows 1,000-fold.
+ - The time required for diagonalization increases nearly **1 billion times**.
+
+This poses significant challenges for **large-scale numerical computations** in fields such as:
+- Defects, impurities, and interfaces.
+- Superlattices, alloys, and clusters.
+- Quasicrystals, fractals, polycrystals, and amorphous systems.
+
+**Breakthrough with TBPLaS**
+Addressing these challenges, **Professor Shengjun Yuan** from **Wuhan University** has:
+- Conducted **over a decade of research** to propose universally applicable computational physics formulas.
+- Developed the **Tight-Binding Propagation Method (TBPM)** and the **TBPLaS** software package.
+
+**Key Features of TBPLaS**
+- **Low-scaling computation**: Overcomes the limitations of traditional diagonalization methods.
+- **Scalable simulations**: Can simulate systems spanning nearly **10 orders of magnitude** in size, including those with billions of atoms (lattice points).
+
+**Collaboration with DeepModeling**
+TBPLaS has officially joined the **DeepModeling community** to:
+- Collaborate with developers and users.
+- Promote the development and application of **large-scale computational physics methods** and **software**.
+
+---
+
+## Basics
+The core idea of the TBPM (Tight-Binding Propagation Method) is as follows: In solid-state physics, a random state in real space contains information about all eigenstates of the system. As the wave function of the random state evolves, each eigenstate evolves independently. However, in terms of physical observables, what is needed is the contribution from a group of eigenstates with similar eigenvalues, not their individual characteristics. Hence, this idea suggests that information from the wave function’s time-domain evolution can be converted into physical quantities of interest, thereby avoiding the diagonalization process. By reducing the computational complexity from \(O(N^3)\) to \(O(N)\), this approach ensures that the linear scaling relationship between computational cost and system size is maintained, even for extremely large systems.
+
+Below is a brief explanation using electronic transport properties as an example. The formula for the electrical conductivity \(\sigma_{AA}(E, \tau)\) is approximately:
+
+\[
+\sigma_{AA}(E, \tau) \approx \frac{1}{\Omega} \rho(E) \int_0^{\tau} dt \, \text{Re} \left[ e^{-iEt} \langle \phi | A e^{iHt} J_A e^{-iHt} | \phi \rangle \right]
+\]
+
+Here:
+- \(|\phi\rangle\) represents a random initial state.
+- \(|\phi(t)\rangle\) is the time-evolved state calculated from \(|\phi\rangle\) (via the time-dependent Schrödinger equation).
+- \(\Omega\) is the system's volume (or area in 2D).
+- \(J_A\) is the \(A\)-direction component of the current operator.
+- \(\rho(E)\) is the electronic density of states (which can be obtained via the spectral correlation function).
+- The time-evolution operator \(e^{iHt}\) is computed using the Chebyshev polynomial expansion method.
+
+The quantity \(\sigma_{AA}(E, \tau)\) is determined by the integral up to the time limit \(\tau\). It provides information about the energy-dependent conductivity, with \(\rho(E)\) describing the contribution of states near energy \(E\). The diffusion coefficient \(D_{AA}(E, \tau)\), derived from this method, captures the dynamics and transport properties over different timescales. Additionally, quantities like the mean free path and localization length can be obtained.
+
+For more computational details, refer to the following articles:
+- *Phys. Rev. B 82, 115448 (2010)* (Electrical, optical, and transport properties)
+- *Phys. Rev. B 84, 035439 (2011)* (Polarization and related quantities)
+- *Phys. Rev. B 91, 045420 (2015)* (Transport properties)
+- *Comput. Phys. Commun. 285, 108632 (2023)* (Summary of the computational methodology for transport properties)
+- *Chin. Phys. Lett. 40, 027101 (2023)* (Automated self-consistent calculations of the electronic density distribution).
+
+---
+## **Features of TBPLaS**
+
+
+**1. Powerful Modeling Capabilities**
+- **Supports diverse models**:
+ - Tight-binding models in arbitrary dimensions, shapes, and boundary conditions.
+ - Molecules, clusters, nanotubes, nanoribbons, 2D crystals, 3D crystals, etc.
+- **Built-in modeling tools**:
+ - Quickly construct complex models like heterojunctions, twisted structures, quasicrystals, and fractals.
+ - Handle defects like vacancies and deformations, as well as external electric and magnetic fields.
+- **Analytical support**:
+ - Derive and use analytical Hamiltonians directly.
+- **Built-in formula libraries**:
+ - **Slater-Koster formula library**: Build tight-binding models directly from atomic structures.
+ - **Spin-orbit coupling formula library**: Support various spin-orbit coupling effects.
+- **Predefined material models**:
+ - Tight-binding models for common materials like graphene, phosphorene, and transition metal dichalcogenides are readily available.
+- **Parameter optimization**:
+ - Fit tight-binding models to band structures obtained from first-principles calculations.
+- **Seamless integration**:
+ - Interface with **Wannier90**: Directly import tight-binding models fitted by Wannier90.
+ - Interface with **LAMMPS**: Import optimized atomic configurations to build tight-binding models.
+ - Interface with **DeePTB** and **DeepH**: Directly import machine-learning-fitted tight-binding models.
+
+ +
+
+**2. Rich Physical Property Calculation Features**
+- **Precise diagonalization methods**:
+ - Calculate band structures, density of states, local density of states, \(Z(2)\) topological invariants, polarizability, dielectric functions, AC (optical) conductivity, and more.
+- **Time-evolution algorithms (TBPM)**:
+ - Simulate real-space wavefunction propagation.
+ - Compute:
+ - Energy density of states, Landau levels, local density of states, quasi-eigenstates.
+ - Optical conductivity, electrical conductivity, magneto-optical conductivity.
+ - Carrier velocity, mobility, mean free path, localization length, diffusion coefficients.
+ - Transmission coefficients, magnetization, magnetic susceptibility.
+ - Polarization functions, response functions, dielectric constants.
+ - Energy loss spectra, plasmon spectra, plasmon lifetime, and spatial electron density distribution.
+- **Kernel Polynomial Method (KPM)**:
+ - Compute DC conductivity and Hall conductivity.
+- **Green’s function methods**:
+ - Calculate the local density of states.
+
+
+**3. High Computational Efficiency**
+- **Optimized performance**:
+ - Core components written in **Cython** and **Fortran**.
+ - Extensive use of **sparse matrices** to reduce memory usage.
+- **High-performance libraries**:
+ - Support for **MKL** and other efficient math libraries.
+- **Parallelization**:
+ - **MPI + OpenMP hybrid parallelization** for optimal hardware resource utilization.
+
+
+**4. Simple and User-Friendly**
+- **Python-based interface**:
+ - Object-oriented design closely tied to physical concepts, reducing the learning curve.
+- **Robust error handling**:
+ - Built-in parameter checks and exception handling for detailed error diagnostics.
+- **Comprehensive documentation**:
+ - The project website provides detailed tutorials and example programs:
+ [TBPLaS Tutorials](http://www.tbplas.net/tutorial/index.html).
+
+## **Recent Applications of TBPLaS in Large-Scale Electronic Structure and Property Research**
+
+**1. Research on Twisted Graphene Structures by Francisco Guinea's Group**
+- **Who**: Professor Francisco Guinea, Foreign Member of the U.S. National Academy of Sciences, and his group at the **IMDEA Research Institute, Spain**.
+- **Published Work**:
+ - *Phys. Rev. Res. 6, 013165 (2024)*.
+ - *arXiv:2401.09010 (2024)*.
+- **Highlights**:
+ - TBPLaS was used to perform large-scale electronic structure and property calculations.
+ - **Topics**:
+ - The mechanism behind the formation of "magic angles" in **twisted multilayer graphene**.
+ - The flat-band properties of **quasicrystals in twisted trilayer graphene**.
+ - **Scale**:
+ - Simulations were conducted on systems with **over 10 million atoms** in the supercell using the **TBPM method**.
+
+
+**2. Research on GaP Crystals by Wei-Nan E and Linfeng Zhang’s Team**
+- **Who**:
+ - Academician **Wei-Nan E** from the **Chinese Academy of Sciences** and **Peking University**.
+ - Linfeng Zhang’s team from the **Beijing Institute for General Artificial Intelligence (BIGAI)**.
+ - Researcher Gu Qiangqiang et al.
+- **Published Work**:
+ - *arXiv:2307.04638*.
+- **Highlights**:
+ - Proposed a deep-learning-based method, **DeePTB**, to construct tight-binding model Hamiltonians.
+ - **Steps**:
+ 1. **Finite-temperature structure sampling**:
+ - Conducted molecular dynamics simulations using **DeePMD** (Deep Potential Molecular Dynamics) to sample structures at finite temperatures.
+ 2. **Hamiltonian construction**:
+ - Constructed tight-binding Hamiltonians using the **DeePTB method**.
+ 3. **Property calculations**:
+ - Leveraged **TBPLaS** and the **TBPM method** to calculate properties of **millions of atoms** in large-scale GaP crystal systems.
+ - **Results**:
+ - Computed finite-temperature **electronic density of states**, **optical conductivity**, **dielectric functions**, and **complex refractive indices**.
+
+
+**Representative Applications of TBPLaS in the Past Five Years**
+**1. 2D Crystals and Quantum Dots**
+- **References**:
+ - *Phys. Rev. X 12, 021055 (2022)*
+ - *Phys. Rev. Lett. 129, 056803 (2022)*
+ - *Phys. Rev. B 108, 045404 (2023)*
+ - *Phys. Rev. B 105, 094111 (2022)*
+ - *Phys. Rev. B 104, 155110 (2021)*
+ - *Phys. Rev. B 98, 155411 (2018)*
+ - *Phys. Rev. B 98, 115117 (2018)*
+ - *Phys. Rev. B 97, 245410 (2018)*
+ - *Phys. Rev. Mater. 2, 114011 (2018)*
+ - *Nanoscale 10, 21918 (2018)*
+
+
+**2. Moiré Superlattice Structures**
+- **References**:
+ - *Science 380, 1367 (2023)*
+ - *Nat. Commun. 11, 371 (2020)*
+ - *Phys. Rev. B 109, 085118 (2024)*
+ - *Nano Lett. 23, 1836 (2023)*
+ - *Phys. Rev. B 108, 045138 (2023)*
+ - *Phys. Rev. B 107, 035109 (2023)*
+ - *Phys. Rev. B 105, 245415 (2022)*
+ - *npj Comput. Mater. 8, 73 (2022)*
+ - *Phys. Rev. B 104, 205104 (2021)*
+ - *Phys. Rev. B 103, 115431 (2021)*
+ - *Sci. China: Phys. Mech. Astron. 64, 267811 (2021)*
+ - *Phys. Rev. B 102, 235418 (2020)*
+ - *Phys. Rev. B 102, 241106 (R) (2020)*
+
+
+**3. Quasicrystals with Rotational Symmetry**
+- **References**:
+ - *Phys. Rev. B 105, 075121 (2022)*
+ - *Phys. Rev. B 105, 125403 (2022)*
+ - *Phys. Rev. B 102, 115123 (2020)*
+ - *Phys. Rev. B 102, 045113 (2020)*
+ - *npj Comput. Mater. 5, 122 (2019)*
+
+
+**4. Fractal Structures with Fractional Spatial Dimensions**
+- **References**:
+ - *Phys. Rev. B 107, 115424 (2023)*
+ - *Phys. Rev. B 105, 205433 (2022)*
+ - *Phys. Rev. B 102, 075440 (2020)*
+ - *Phys. Rev. B 102, 245425 (2020)*
+ - *Phys. Rev. B 101, 045413 (2020)*
+ - *Phys. Rev. B 99, 075402 (2019)*
+ - *Phys. Rev. B 97, 205434 (2018)*
+
+---
+
+## **Future Development Directions for TBPLaS**
+
+**1. Algorithm Development for Strongly Correlated Systems**
+- Implementation of algorithms for **strongly correlated systems**, including:
+ - **Hubbard models**.
+ - **Self-consistent iterative methods**.
+
+
+**2. Code Refactoring**
+- Refactor legacy code in **C++**:
+ - Simplify the installation process.
+ - Improve code maintainability and readability.
+
+
+**3. High-Performance C++ User Interfaces**
+- Develop a comprehensive **C++ user interface** for scenarios requiring extremely high performance.
+
+
+**4. Deep Collaboration with the DeepModeling Community**
+- Foster deeper integration with other software in the **DeepModeling community**, enabling seamless workflows for:
+ - **First-principles modeling** to **large-scale property calculations**.
+ - Full integration of the toolchain:
+ - **ABACUS**: First-principles calculations.
+ - **DeePTB**: Tight-binding Hamiltonian construction via deep learning.
+ - **DeePMD**: Molecular dynamics simulations.
+ - **TBPLaS**: Tight-binding simulations and large-scale property calculations.
+
+
+
+
+
diff --git a/source/_posts/jax_fem.md b/source/_posts/jax_fem.md
new file mode 100644
index 00000000..f215638f
--- /dev/null
+++ b/source/_posts/jax_fem.md
@@ -0,0 +1,68 @@
+---
+title: "JAX-FEM | Advancing Development Towards Large-Scale Problem Solving"
+date: 2024-02-05
+categories:
+- JAX-FEM
+mathjax: true
+---
+"The integration of machine learning and physical modeling is revolutionizing the paradigm of scientific research. People aiming to push the boundaries of science and solve challenging problems through computational modeling are coming together in unprecedented ways." Recently, the DeepModeling open-source community has welcomed a new member in the field of macro-scale computation. To further advance the development of the JAX-FEM project, a differentiable finite element method library, JAX-FEM will join the DeepModeling community. Together with developers and users in the community, it aims to expand the frontiers of finite element methods in the AI4Science era.
+
+Community project homepage:
+https://github.com/deepmodeling/jax-fem
+
+
+
+### **Finite Element Method (FEM):**
+ FEM is a representative physical modeling technique widely applied in engineering manufacturing and industrial design. It divides the entire problem domain into subdomains, defines basis functions over each subdomain, and combines the finite elements to approximate the solution of the original equations. FEM is effectively used in structural analysis, fluid dynamics, heat transfer, and electromagnetic problems for solving partial differential equations numerically.
+
+### Challenges in Conventional FEM:
+Despite its widespread application, FEM faces challenges as problem scales grow. These challenges include increased computational complexity and memory requirements, leading to prolonged computational times and excessive resource consumption. Additionally, the user-friendliness of interfaces (e.g., explicit derivation of linear incremental forms for solving nonlinear problems) and the extensibility of code interfaces (e.g., integration with data-driven models) in many commercial and open-source FEM software are limited.
+
+### **What is JAX-FEM?**
+JAX-FEM is designed to overcome these limitations. By utilizing Google’s JAX library—a high-performance numerical computing and machine learning toolkit—the developers have created an extensible FEM solution written entirely in Python. This enables efficient solving of nonlinear finite element problems.
+
+
+
+
+**2. Rich Physical Property Calculation Features**
+- **Precise diagonalization methods**:
+ - Calculate band structures, density of states, local density of states, \(Z(2)\) topological invariants, polarizability, dielectric functions, AC (optical) conductivity, and more.
+- **Time-evolution algorithms (TBPM)**:
+ - Simulate real-space wavefunction propagation.
+ - Compute:
+ - Energy density of states, Landau levels, local density of states, quasi-eigenstates.
+ - Optical conductivity, electrical conductivity, magneto-optical conductivity.
+ - Carrier velocity, mobility, mean free path, localization length, diffusion coefficients.
+ - Transmission coefficients, magnetization, magnetic susceptibility.
+ - Polarization functions, response functions, dielectric constants.
+ - Energy loss spectra, plasmon spectra, plasmon lifetime, and spatial electron density distribution.
+- **Kernel Polynomial Method (KPM)**:
+ - Compute DC conductivity and Hall conductivity.
+- **Green’s function methods**:
+ - Calculate the local density of states.
+
+
+**3. High Computational Efficiency**
+- **Optimized performance**:
+ - Core components written in **Cython** and **Fortran**.
+ - Extensive use of **sparse matrices** to reduce memory usage.
+- **High-performance libraries**:
+ - Support for **MKL** and other efficient math libraries.
+- **Parallelization**:
+ - **MPI + OpenMP hybrid parallelization** for optimal hardware resource utilization.
+
+
+**4. Simple and User-Friendly**
+- **Python-based interface**:
+ - Object-oriented design closely tied to physical concepts, reducing the learning curve.
+- **Robust error handling**:
+ - Built-in parameter checks and exception handling for detailed error diagnostics.
+- **Comprehensive documentation**:
+ - The project website provides detailed tutorials and example programs:
+ [TBPLaS Tutorials](http://www.tbplas.net/tutorial/index.html).
+
+## **Recent Applications of TBPLaS in Large-Scale Electronic Structure and Property Research**
+
+**1. Research on Twisted Graphene Structures by Francisco Guinea's Group**
+- **Who**: Professor Francisco Guinea, Foreign Member of the U.S. National Academy of Sciences, and his group at the **IMDEA Research Institute, Spain**.
+- **Published Work**:
+ - *Phys. Rev. Res. 6, 013165 (2024)*.
+ - *arXiv:2401.09010 (2024)*.
+- **Highlights**:
+ - TBPLaS was used to perform large-scale electronic structure and property calculations.
+ - **Topics**:
+ - The mechanism behind the formation of "magic angles" in **twisted multilayer graphene**.
+ - The flat-band properties of **quasicrystals in twisted trilayer graphene**.
+ - **Scale**:
+ - Simulations were conducted on systems with **over 10 million atoms** in the supercell using the **TBPM method**.
+
+
+**2. Research on GaP Crystals by Wei-Nan E and Linfeng Zhang’s Team**
+- **Who**:
+ - Academician **Wei-Nan E** from the **Chinese Academy of Sciences** and **Peking University**.
+ - Linfeng Zhang’s team from the **Beijing Institute for General Artificial Intelligence (BIGAI)**.
+ - Researcher Gu Qiangqiang et al.
+- **Published Work**:
+ - *arXiv:2307.04638*.
+- **Highlights**:
+ - Proposed a deep-learning-based method, **DeePTB**, to construct tight-binding model Hamiltonians.
+ - **Steps**:
+ 1. **Finite-temperature structure sampling**:
+ - Conducted molecular dynamics simulations using **DeePMD** (Deep Potential Molecular Dynamics) to sample structures at finite temperatures.
+ 2. **Hamiltonian construction**:
+ - Constructed tight-binding Hamiltonians using the **DeePTB method**.
+ 3. **Property calculations**:
+ - Leveraged **TBPLaS** and the **TBPM method** to calculate properties of **millions of atoms** in large-scale GaP crystal systems.
+ - **Results**:
+ - Computed finite-temperature **electronic density of states**, **optical conductivity**, **dielectric functions**, and **complex refractive indices**.
+
+
+**Representative Applications of TBPLaS in the Past Five Years**
+**1. 2D Crystals and Quantum Dots**
+- **References**:
+ - *Phys. Rev. X 12, 021055 (2022)*
+ - *Phys. Rev. Lett. 129, 056803 (2022)*
+ - *Phys. Rev. B 108, 045404 (2023)*
+ - *Phys. Rev. B 105, 094111 (2022)*
+ - *Phys. Rev. B 104, 155110 (2021)*
+ - *Phys. Rev. B 98, 155411 (2018)*
+ - *Phys. Rev. B 98, 115117 (2018)*
+ - *Phys. Rev. B 97, 245410 (2018)*
+ - *Phys. Rev. Mater. 2, 114011 (2018)*
+ - *Nanoscale 10, 21918 (2018)*
+
+
+**2. Moiré Superlattice Structures**
+- **References**:
+ - *Science 380, 1367 (2023)*
+ - *Nat. Commun. 11, 371 (2020)*
+ - *Phys. Rev. B 109, 085118 (2024)*
+ - *Nano Lett. 23, 1836 (2023)*
+ - *Phys. Rev. B 108, 045138 (2023)*
+ - *Phys. Rev. B 107, 035109 (2023)*
+ - *Phys. Rev. B 105, 245415 (2022)*
+ - *npj Comput. Mater. 8, 73 (2022)*
+ - *Phys. Rev. B 104, 205104 (2021)*
+ - *Phys. Rev. B 103, 115431 (2021)*
+ - *Sci. China: Phys. Mech. Astron. 64, 267811 (2021)*
+ - *Phys. Rev. B 102, 235418 (2020)*
+ - *Phys. Rev. B 102, 241106 (R) (2020)*
+
+
+**3. Quasicrystals with Rotational Symmetry**
+- **References**:
+ - *Phys. Rev. B 105, 075121 (2022)*
+ - *Phys. Rev. B 105, 125403 (2022)*
+ - *Phys. Rev. B 102, 115123 (2020)*
+ - *Phys. Rev. B 102, 045113 (2020)*
+ - *npj Comput. Mater. 5, 122 (2019)*
+
+
+**4. Fractal Structures with Fractional Spatial Dimensions**
+- **References**:
+ - *Phys. Rev. B 107, 115424 (2023)*
+ - *Phys. Rev. B 105, 205433 (2022)*
+ - *Phys. Rev. B 102, 075440 (2020)*
+ - *Phys. Rev. B 102, 245425 (2020)*
+ - *Phys. Rev. B 101, 045413 (2020)*
+ - *Phys. Rev. B 99, 075402 (2019)*
+ - *Phys. Rev. B 97, 205434 (2018)*
+
+---
+
+## **Future Development Directions for TBPLaS**
+
+**1. Algorithm Development for Strongly Correlated Systems**
+- Implementation of algorithms for **strongly correlated systems**, including:
+ - **Hubbard models**.
+ - **Self-consistent iterative methods**.
+
+
+**2. Code Refactoring**
+- Refactor legacy code in **C++**:
+ - Simplify the installation process.
+ - Improve code maintainability and readability.
+
+
+**3. High-Performance C++ User Interfaces**
+- Develop a comprehensive **C++ user interface** for scenarios requiring extremely high performance.
+
+
+**4. Deep Collaboration with the DeepModeling Community**
+- Foster deeper integration with other software in the **DeepModeling community**, enabling seamless workflows for:
+ - **First-principles modeling** to **large-scale property calculations**.
+ - Full integration of the toolchain:
+ - **ABACUS**: First-principles calculations.
+ - **DeePTB**: Tight-binding Hamiltonian construction via deep learning.
+ - **DeePMD**: Molecular dynamics simulations.
+ - **TBPLaS**: Tight-binding simulations and large-scale property calculations.
+
+
+
+
+
diff --git a/source/_posts/jax_fem.md b/source/_posts/jax_fem.md
new file mode 100644
index 00000000..f215638f
--- /dev/null
+++ b/source/_posts/jax_fem.md
@@ -0,0 +1,68 @@
+---
+title: "JAX-FEM | Advancing Development Towards Large-Scale Problem Solving"
+date: 2024-02-05
+categories:
+- JAX-FEM
+mathjax: true
+---
+"The integration of machine learning and physical modeling is revolutionizing the paradigm of scientific research. People aiming to push the boundaries of science and solve challenging problems through computational modeling are coming together in unprecedented ways." Recently, the DeepModeling open-source community has welcomed a new member in the field of macro-scale computation. To further advance the development of the JAX-FEM project, a differentiable finite element method library, JAX-FEM will join the DeepModeling community. Together with developers and users in the community, it aims to expand the frontiers of finite element methods in the AI4Science era.
+
+Community project homepage:
+https://github.com/deepmodeling/jax-fem
+
+
+
+### **Finite Element Method (FEM):**
+ FEM is a representative physical modeling technique widely applied in engineering manufacturing and industrial design. It divides the entire problem domain into subdomains, defines basis functions over each subdomain, and combines the finite elements to approximate the solution of the original equations. FEM is effectively used in structural analysis, fluid dynamics, heat transfer, and electromagnetic problems for solving partial differential equations numerically.
+
+### Challenges in Conventional FEM:
+Despite its widespread application, FEM faces challenges as problem scales grow. These challenges include increased computational complexity and memory requirements, leading to prolonged computational times and excessive resource consumption. Additionally, the user-friendliness of interfaces (e.g., explicit derivation of linear incremental forms for solving nonlinear problems) and the extensibility of code interfaces (e.g., integration with data-driven models) in many commercial and open-source FEM software are limited.
+
+### **What is JAX-FEM?**
+JAX-FEM is designed to overcome these limitations. By utilizing Google’s JAX library—a high-performance numerical computing and machine learning toolkit—the developers have created an extensible FEM solution written entirely in Python. This enables efficient solving of nonlinear finite element problems.
+
+ +
+
+---
+
+### **Key Features and Advantages of JAX-FEM**
+
+1. **Interactivity and Extensibility:**
+ Unlike most existing FEM libraries implemented in low-level languages like C/C++ or Fortran, JAX-FEM is developed in pure Python. This significantly enhances development flexibility and ease of use, providing a streamlined experience for both users and developers.
+
+2. **GPU Acceleration:**
+ JAX-FEM can leverage GPUs for accelerated computation, which is particularly useful for problems with a large number of degrees of freedom (DOF). Supported by JAX’s XLA backend for linear algebra acceleration, JAX-FEM achieves competitive performance, especially when GPUs are available. For example, in a 3D tensile loading problem with 7.7 million DOF, JAX-FEM’s GPU-based computation is approximately 10 times faster than commercial FEM software.
+
+3. **Automatic Differentiation (AD):**
+ JAX-FEM incorporates AD technology, eliminating the need for manual derivation of sensitivity or Jacobian matrices. This simplifies solving nonlinear and inverse problems, automating complex mathematical operations. It is particularly useful in areas like engineering optimization and parameter identification.
+
+
+
+
+---
+
+### **Key Features and Advantages of JAX-FEM**
+
+1. **Interactivity and Extensibility:**
+ Unlike most existing FEM libraries implemented in low-level languages like C/C++ or Fortran, JAX-FEM is developed in pure Python. This significantly enhances development flexibility and ease of use, providing a streamlined experience for both users and developers.
+
+2. **GPU Acceleration:**
+ JAX-FEM can leverage GPUs for accelerated computation, which is particularly useful for problems with a large number of degrees of freedom (DOF). Supported by JAX’s XLA backend for linear algebra acceleration, JAX-FEM achieves competitive performance, especially when GPUs are available. For example, in a 3D tensile loading problem with 7.7 million DOF, JAX-FEM’s GPU-based computation is approximately 10 times faster than commercial FEM software.
+
+3. **Automatic Differentiation (AD):**
+ JAX-FEM incorporates AD technology, eliminating the need for manual derivation of sensitivity or Jacobian matrices. This simplifies solving nonlinear and inverse problems, automating complex mathematical operations. It is particularly useful in areas like engineering optimization and parameter identification.
+
+ +
+4. **Integration with Machine Learning:**
+ Beyond being a finite element solver, JAX-FEM effectively integrates machine learning capabilities. Users can seamlessly train and deploy models on a single platform, enabling data-driven computational mechanics research.
+
+5. **Open Source and Community Support:**
+ As an open-source project, JAX-FEM encourages contributions and collaboration. Users can freely access the source code, customize it according to their needs, and share improvements and applications with others.
+
+
+
+4. **Integration with Machine Learning:**
+ Beyond being a finite element solver, JAX-FEM effectively integrates machine learning capabilities. Users can seamlessly train and deploy models on a single platform, enabling data-driven computational mechanics research.
+
+5. **Open Source and Community Support:**
+ As an open-source project, JAX-FEM encourages contributions and collaboration. Users can freely access the source code, customize it according to their needs, and share improvements and applications with others.
+
+ +
+---
+
+### **Joining and Using JAX-FEM**
+JAX-FEM has joined the DeepModeling open-source community. The project is hosted at:
+[https://github.com/deepmodeling/jax-fem](https://github.com/deepmodeling/jax-fem)
+
+---
+
+### **Future Development Plans**
+The upcoming development of JAX-FEM will revolve around solving ultra-large-scale problems using CPU/GPU hybrid parallelization and integrating third-party linear solvers to maximize computational efficiency. The project will also explore machine-learning-based multiscale computational problems, organically combining FEM as a macro-scale tool with other micro-scale tools.
+
+In summary, JAX-FEM combines modern computing techniques and automatic differentiation, offering a powerful and efficient tool for automating finite element analysis workflows, particularly in scenarios involving complex physical phenomena and material behaviors.
+
+If you are interested in contributing to the development of differentiable FEM algorithms and frameworks, the development team warmly invites you to connect with them.
+
+---
+
+**Reference:**
+Xue, T., Liao, S., Gan, Z., Park, C., Xie, X., Liu, W. K., & Cao, J. (2023). *JAX-FEM: A differentiable GPU-accelerated 3D finite element solver for automatic inverse design and mechanistic data science.* Computer Physics Communications, 108802.
\ No newline at end of file
+
+---
+
+### **Joining and Using JAX-FEM**
+JAX-FEM has joined the DeepModeling open-source community. The project is hosted at:
+[https://github.com/deepmodeling/jax-fem](https://github.com/deepmodeling/jax-fem)
+
+---
+
+### **Future Development Plans**
+The upcoming development of JAX-FEM will revolve around solving ultra-large-scale problems using CPU/GPU hybrid parallelization and integrating third-party linear solvers to maximize computational efficiency. The project will also explore machine-learning-based multiscale computational problems, organically combining FEM as a macro-scale tool with other micro-scale tools.
+
+In summary, JAX-FEM combines modern computing techniques and automatic differentiation, offering a powerful and efficient tool for automating finite element analysis workflows, particularly in scenarios involving complex physical phenomena and material behaviors.
+
+If you are interested in contributing to the development of differentiable FEM algorithms and frameworks, the development team warmly invites you to connect with them.
+
+---
+
+**Reference:**
+Xue, T., Liao, S., Gan, Z., Park, C., Xie, X., Liu, W. K., & Cao, J. (2023). *JAX-FEM: A differentiable GPU-accelerated 3D finite element solver for automatic inverse design and mechanistic data science.* Computer Physics Communications, 108802.
\ No newline at end of file






