diff --git a/solution/1000-1099/1035.Uncrossed Lines/README.md b/solution/1000-1099/1035.Uncrossed Lines/README.md index a5b523e771cd3..5d903db95ac83 100644 --- a/solution/1000-1099/1035.Uncrossed Lines/README.md +++ b/solution/1000-1099/1035.Uncrossed Lines/README.md @@ -39,7 +39,7 @@ tags: 
 输入：nums1 = [1,4,2], nums2 = [1,2,4]
 输出：2
-解释：可以画出两条不交叉的线，如上图所示。
+解释：可以画出两条不交叉的线，如上图所示。 
 但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。
diff --git a/solution/3200-3299/3248.Snake in Matrix/README.md b/solution/3200-3299/3248.Snake in Matrix/README.md new file mode 100644 index 0000000000000..b77f4b733962a --- /dev/null +++ b/solution/3200-3299/3248.Snake in Matrix/README.md @@ -0,0 +1,293 @@ +--- +comments: true +difficulty: 简单 +edit_url: https://github.com/doocs/leetcode/edit/main/solution/3200-3299/3248.Snake%20in%20Matrix/README.md +--- + + + +# [3248. 矩阵中的蛇](https://leetcode.cn/problems/snake-in-matrix) + +[English Version](/solution/3200-3299/3248.Snake%20in%20Matrix/README_EN.md) + +## 题目描述 + + + +

大小为 n x n 的矩阵 grid 中有一条蛇。蛇可以朝 四个可能的方向 移动。矩阵中的每个单元格都使用位置进行标识： grid[i][j] = (i * n) + j。

+ +

蛇从单元格 0 开始，并遵循一系列命令移动。

+ +

给你一个整数 n 表示 grid 的大小，另给你一个字符串数组 commands，其中包括 "UP"、"RIGHT"、"DOWN" 和 "LEFT"。题目测评数据保证蛇在整个移动过程中将始终位于 grid 边界内。

+ +

返回执行 commands 后蛇所停留的最终单元格的位置。

+ +

 

+ +

示例 1：

+ +
+

输入：n = 2, commands = ["RIGHT","DOWN"]

+ +

输出：3

+ +

解释：

+ +
+ + + + + + + + + + + +
01
23
+ + + + + + + + + + + + +
01
23
+ + + + + + + + + + + + +
01
23
+
+
+ +

示例 2：

+ +
+

输入：n = 3, commands = ["DOWN","RIGHT","UP"]

+ +

输出：1

+ +

解释：

+ +
+ + + + + + + + + + + + + + + + + + +
012
345
678
+ + + + + + + + + + + + + + + + + + + +
012
345
678
+ + + + + + + + + + + + + + + + + + + +
012
345
678
+ + + + + + + + + + + + + + + + + + + +
012
345
678
+
+
+ +

 

+ +

提示：

+ + + + + +## 解法 + + + +### 方法一：模拟 + +我们可以用两个变量 $x$ 和 $y$ 来表示蛇的位置，初始时 $x = y = 0$，然后遍历 $\textit{commands}$，根据当前的命令更新 $x$ 和 $y$ 的值，最后返回 $x \times n + y$ 即可。 + +时间复杂度 $O(n)$，其中 $n$ 是数组 $\textit{commands}$ 的长度。空间复杂度 $O(1)$。 + + + +#### Python3 + +```python +class Solution: + def finalPositionOfSnake(self, n: int, commands: List[str]) -> int: + x = y = 0 + for c in commands: + match c[0]: + case "U": + x -= 1 + case "D": + x += 1 + case "L": + y -= 1 + case "R": + y += 1 + return x * n + y +``` + +#### Java + +```java +class Solution { + public int finalPositionOfSnake(int n, List commands) { + int x = 0, y = 0; + for (var c : commands) { + switch (c.charAt(0)) { + case 'U' -> x--; + case 'D' -> x++; + case 'L' -> y--; + case 'R' -> y++; + } + } + return x * n + y; + } +} +``` + +#### C++ + +```cpp +class Solution { +public: + int finalPositionOfSnake(int n, vector& commands) { + int x = 0, y = 0; + for (const auto& c : commands) { + switch (c[0]) { + case 'U': x--; break; + case 'D': x++; break; + case 'L': y--; break; + case 'R': y++; break; + } + } + return x * n + y; + } +}; +``` + +#### Go + +```go +func finalPositionOfSnake(n int, commands []string) int { + x, y := 0, 0 + for _, c := range commands { + switch c[0] { + case 'U': + x-- + case 'D': + x++ + case 'L': + y-- + case 'R': + y++ + } + } + return x*n + y +} +``` + +#### TypeScript + +```ts +function finalPositionOfSnake(n: number, commands: string[]): number { + let [x, y] = [0, 0]; + for (const c of commands) { + c[0] === 'U' && x--; + c[0] === 'D' && x++; + c[0] === 'L' && y--; + c[0] === 'R' && y++; + } + return x * n + y; +} +``` + + + + + + diff --git a/solution/3200-3299/3248.Snake in Matrix/README_EN.md b/solution/3200-3299/3248.Snake in Matrix/README_EN.md new file mode 100644 index 0000000000000..b08375121cd2b --- /dev/null +++ b/solution/3200-3299/3248.Snake in Matrix/README_EN.md @@ -0,0 +1,291 @@ +--- +comments: true +difficulty: Easy +edit_url: https://github.com/doocs/leetcode/edit/main/solution/3200-3299/3248.Snake%20in%20Matrix/README_EN.md +--- + + + +# [3248. Snake in Matrix](https://leetcode.com/problems/snake-in-matrix) + +[中文文档](/solution/3200-3299/3248.Snake%20in%20Matrix/README.md) + +## Description + + + +

There is a snake in an n x n matrix grid and can move in four possible directions. Each cell in the grid is identified by the position: grid[i][j] = (i * n) + j.

+ +

The snake starts at cell 0 and follows a sequence of commands.

+ +

You are given an integer n representing the size of the grid and an array of strings commands where each command[i] is either "UP", "RIGHT", "DOWN", and "LEFT". It's guaranteed that the snake will remain within the grid boundaries throughout its movement.

+ +

Return the position of the final cell where the snake ends up after executing commands.

+ +

 

+

Example 1:

+ +
+

Input: n = 2, commands = ["RIGHT","DOWN"]

+ +

Output: 3

+ +

Explanation:

+ +
+ + + + + + + + + + + +
01
23
+ + + + + + + + + + + + +
01
23
+ + + + + + + + + + + + +
01
23
+
+
+ +

Example 2:

+ +
+

Input: n = 3, commands = ["DOWN","RIGHT","UP"]

+ +

Output: 1

+ +

Explanation:

+ +
+ + + + + + + + + + + + + + + + + + +
012
345
678
+ + + + + + + + + + + + + + + + + + + +
012
345
678
+ + + + + + + + + + + + + + + + + + + +
012
345
678
+ + + + + + + + + + + + + + + + + + + +
012
345
678
+
+
+ +

 

+

Constraints:

+ + + + + +## Solutions + + + +### Solution 1: Simulation + +We can use two variables $x$ and $y$ to represent the position of the snake. Initially, $x = y = 0$. Then, we traverse $\textit{commands}$ and update the values of $x$ and $y$ based on the current command. Finally, we return $x \times n + y$. + +The time complexity is $O(n)$, where $n$ is the length of the array $\textit{commands}$. The space complexity is $O(1)$. + + + +#### Python3 + +```python +class Solution: + def finalPositionOfSnake(self, n: int, commands: List[str]) -> int: + x = y = 0 + for c in commands: + match c[0]: + case "U": + x -= 1 + case "D": + x += 1 + case "L": + y -= 1 + case "R": + y += 1 + return x * n + y +``` + +#### Java + +```java +class Solution { + public int finalPositionOfSnake(int n, List commands) { + int x = 0, y = 0; + for (var c : commands) { + switch (c.charAt(0)) { + case 'U' -> x--; + case 'D' -> x++; + case 'L' -> y--; + case 'R' -> y++; + } + } + return x * n + y; + } +} +``` + +#### C++ + +```cpp +class Solution { +public: + int finalPositionOfSnake(int n, vector& commands) { + int x = 0, y = 0; + for (const auto& c : commands) { + switch (c[0]) { + case 'U': x--; break; + case 'D': x++; break; + case 'L': y--; break; + case 'R': y++; break; + } + } + return x * n + y; + } +}; +``` + +#### Go + +```go +func finalPositionOfSnake(n int, commands []string) int { + x, y := 0, 0 + for _, c := range commands { + switch c[0] { + case 'U': + x-- + case 'D': + x++ + case 'L': + y-- + case 'R': + y++ + } + } + return x*n + y +} +``` + +#### TypeScript + +```ts +function finalPositionOfSnake(n: number, commands: string[]): number { + let [x, y] = [0, 0]; + for (const c of commands) { + c[0] === 'U' && x--; + c[0] === 'D' && x++; + c[0] === 'L' && y--; + c[0] === 'R' && y++; + } + return x * n + y; +} +``` + + + + + + diff --git a/solution/3200-3299/3248.Snake in Matrix/Solution.cpp b/solution/3200-3299/3248.Snake in Matrix/Solution.cpp new file mode 100644 index 0000000000000..76bf76325ff9a --- /dev/null +++ b/solution/3200-3299/3248.Snake in Matrix/Solution.cpp @@ -0,0 +1,15 @@ +class Solution { +public: + int finalPositionOfSnake(int n, vector& commands) { + int x = 0, y = 0; + for (const auto& c : commands) { + switch (c[0]) { + case 'U': x--; break; + case 'D': x++; break; + case 'L': y--; break; + case 'R': y++; break; + } + } + return x * n + y; + } +}; diff --git a/solution/3200-3299/3248.Snake in Matrix/Solution.go b/solution/3200-3299/3248.Snake in Matrix/Solution.go new file mode 100644 index 0000000000000..14125f00d9be8 --- /dev/null +++ b/solution/3200-3299/3248.Snake in Matrix/Solution.go @@ -0,0 +1,16 @@ +func finalPositionOfSnake(n int, commands []string) int { + x, y := 0, 0 + for _, c := range commands { + switch c[0] { + case 'U': + x-- + case 'D': + x++ + case 'L': + y-- + case 'R': + y++ + } + } + return x*n + y +} diff --git a/solution/3200-3299/3248.Snake in Matrix/Solution.java b/solution/3200-3299/3248.Snake in Matrix/Solution.java new file mode 100644 index 0000000000000..52f6251492a6f --- /dev/null +++ b/solution/3200-3299/3248.Snake in Matrix/Solution.java @@ -0,0 +1,14 @@ +class Solution { + public int finalPositionOfSnake(int n, List commands) { + int x = 0, y = 0; + for (var c : commands) { + switch (c.charAt(0)) { + case 'U' -> x--; + case 'D' -> x++; + case 'L' -> y--; + case 'R' -> y++; + } + } + return x * n + y; + } +} diff --git a/solution/3200-3299/3248.Snake in Matrix/Solution.py b/solution/3200-3299/3248.Snake in Matrix/Solution.py new file mode 100644 index 0000000000000..2063c455b24d1 --- /dev/null +++ b/solution/3200-3299/3248.Snake in Matrix/Solution.py @@ -0,0 +1,14 @@ +class Solution: + def finalPositionOfSnake(self, n: int, commands: List[str]) -> int: + x = y = 0 + for c in commands: + match c[0]: + case "U": + x -= 1 + case "D": + x += 1 + case "L": + y -= 1 + case "R": + y += 1 + return x * n + y diff --git a/solution/3200-3299/3248.Snake in Matrix/Solution.ts b/solution/3200-3299/3248.Snake in Matrix/Solution.ts new file mode 100644 index 0000000000000..26c4b7e17792c --- /dev/null +++ b/solution/3200-3299/3248.Snake in Matrix/Solution.ts @@ -0,0 +1,10 @@ +function finalPositionOfSnake(n: number, commands: string[]): number { + let [x, y] = [0, 0]; + for (const c of commands) { + c[0] === 'U' && x--; + c[0] === 'D' && x++; + c[0] === 'L' && y--; + c[0] === 'R' && y++; + } + return x * n + y; +} diff --git a/solution/3200-3299/3249.Count the Number of Good Nodes/README.md b/solution/3200-3299/3249.Count the Number of Good Nodes/README.md new file mode 100644 index 0000000000000..f863e25fea1e8 --- /dev/null +++ b/solution/3200-3299/3249.Count the Number of Good Nodes/README.md @@ -0,0 +1,274 @@ +--- +comments: true +difficulty: 中等 +edit_url: https://github.com/doocs/leetcode/edit/main/solution/3200-3299/3249.Count%20the%20Number%20of%20Good%20Nodes/README.md +--- + + + +# [3249. 统计好节点的数目](https://leetcode.cn/problems/count-the-number-of-good-nodes) + +[English Version](/solution/3200-3299/3249.Count%20the%20Number%20of%20Good%20Nodes/README_EN.md) + +## 题目描述 + + + +

现有一棵 无向 树，树中包含 n 个节点，按从 0 到 n - 1 标记。树的根节点是节点 0 。给你一个长度为 n - 1 的二维整数数组 edges，其中 edges[i] = [ai, bi] 表示树中节点 ai 与节点 bi 之间存在一条边。

+ +

如果一个节点的所有子节点为根的 子树 包含的节点数相同，则认为该节点是一个 好节点。

+ +

返回给定树中 好节点 的数量。

+ +

子树 指的是一个节点以及它所有后代节点构成的一棵树。

+ +

 

+ +

 

+ +

示例 1：

+ +
+

输入：edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]

+ +

输出：7

+ +

说明：

+ +

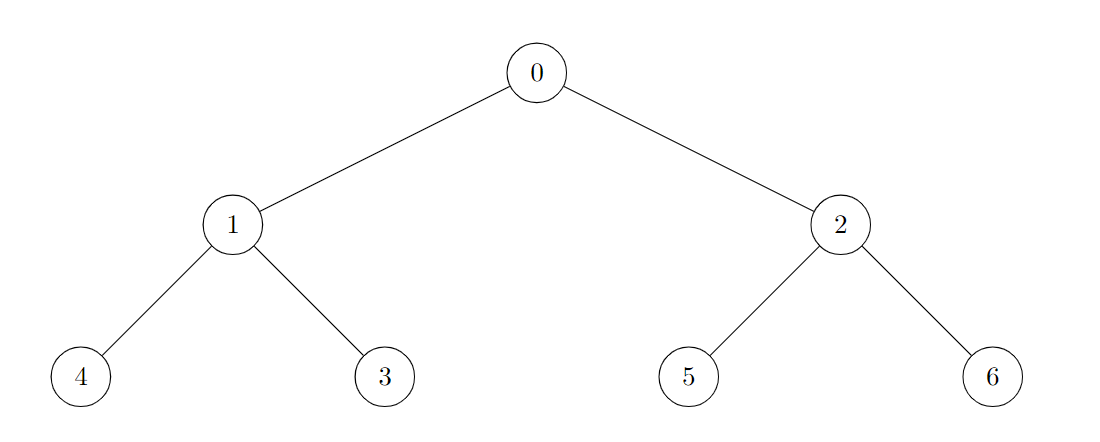树的所有节点都是好节点。

+
+ +

示例 2：

+ +
+

输入：edges = [[0,1],[1,2],[2,3],[3,4],[0,5],[1,6],[2,7],[3,8]]

+ +

输出：6

+ +

说明：

+ +

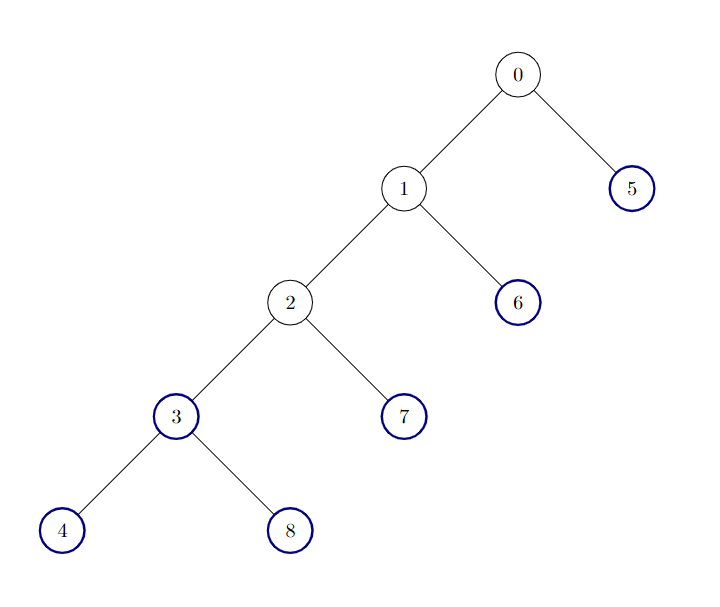树中有 6 个好节点。上图中已将这些节点着色。

+
+ +

示例 3：

+ +
+

输入：edges = [[0,1],[1,2],[1,3],[1,4],[0,5],[5,6],[6,7],[7,8],[0,9],[9,10],[9,12],[10,11]]

+ +

输出：12

+ +

解释：

+ +

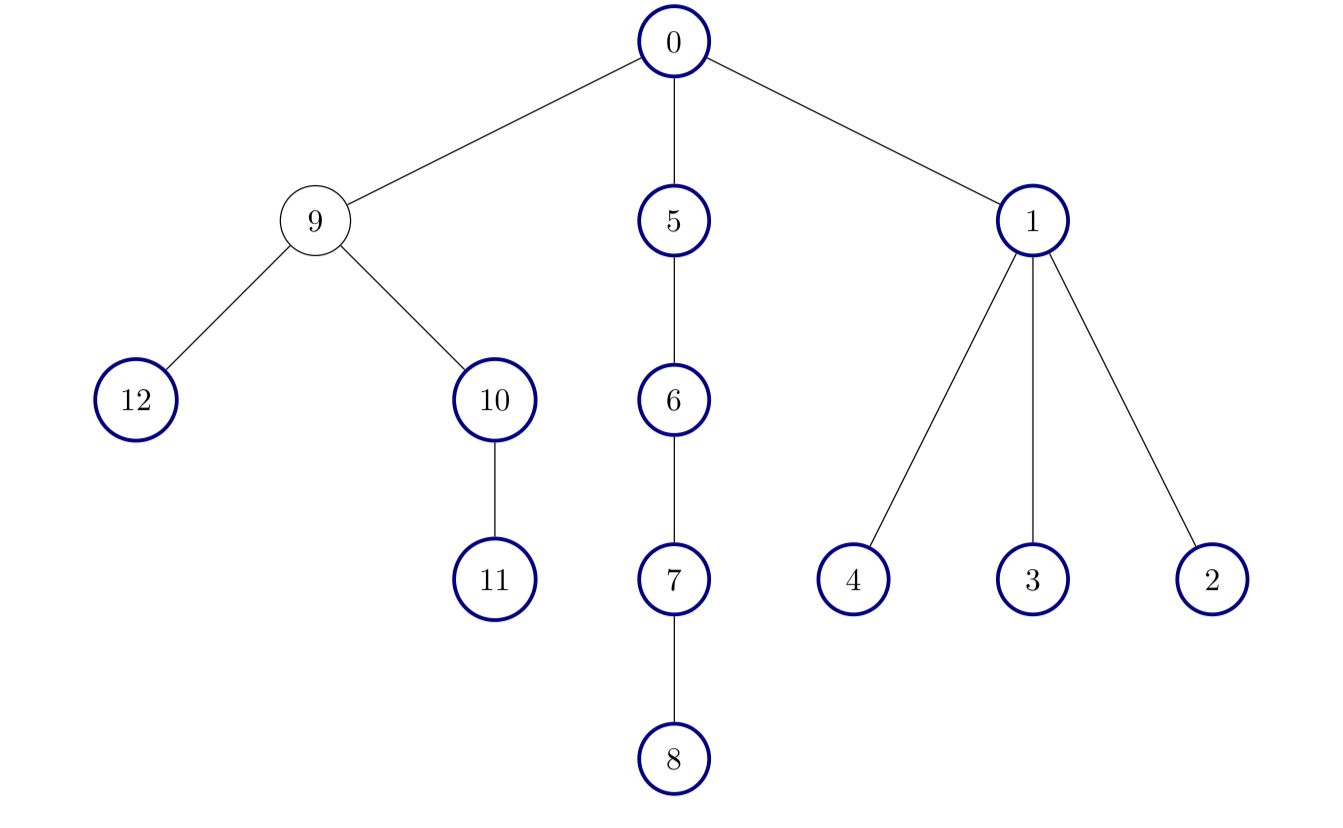除了节点 9 以外其他所有节点都是好节点。

+
+ +

 

+ +

提示：

+ +
    +
  • 2 <= n <= 105
    • +
  • edges.length == n - 1
    • +
  • edges[i].length == 2
    • +
  • 0 <= ai, bi < n
    • +
  • 输入确保 edges 总表示一棵有效的树。
    • +
+ + + +## 解法 + + + +### 方法一：DFS + +我们先根据题目给定的边 $\textit{edges}$ 构建出树的邻接表 $\textit{g}$，其中 $\textit{g}[a]$ 表示节点 $a$ 的所有邻居节点。 + +然后，我们设计一个函数 $\textit{dfs}(a, \textit{fa})$，表示计算以节点 $a$ 为根的子树中的节点数，并累计好节点的数量。其中 $\textit{fa}$ 表示节点 $a$ 的父节点。 + +函数 $\textit{dfs}(a, \textit{fa})$ 的执行过程如下： + +1. 初始化变量 $\textit{pre} = -1$, $\textit{cnt} = 1$, $\textit{ok} = 1$，分别表示节点 $a$ 的某个子树的节点数、节点 $a$ 的所有子树的节点数、以及节点 $a$ 是否为好节点。 +2. 遍历节点 $a$ 的所有邻居节点 $b$，如果 $b$ 不等于 $\textit{fa}$，则递归调用 $\textit{dfs}(b, a)$，返回值为 $\textit{cur}$，并累加到 $\textit{cnt}$ 中。如果 $\textit{pre} < 0$，则将 $\textit{cur}$ 赋值给 $\textit{pre}$；否则，如果 $\textit{pre}$ 不等于 $\textit{cur}$，说明节点 $a$ 的不同子树的节点数不同，将 $\textit{ok}$ 置为 $0$。 +3. 最后，累加 $\textit{ok}$ 到答案中，并返回 $\textit{cnt}$。 + +在主函数中，我们调用 $\textit{dfs}(0, -1)$，最后返回答案。 + +时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 表示节点的数量。 + + + +#### Python3 + +```python +class Solution: + def countGoodNodes(self, edges: List[List[int]]) -> int: + def dfs(a: int, fa: int) -> int: + pre = -1 + cnt = ok = 1 + for b in g[a]: + if b != fa: + cur = dfs(b, a) + cnt += cur + if pre < 0: + pre = cur + elif pre != cur: + ok = 0 + nonlocal ans + ans += ok + return cnt + + g = defaultdict(list) + for a, b in edges: + g[a].append(b) + g[b].append(a) + ans = 0 + dfs(0, -1) + return ans +``` + +#### Java + +```java +class Solution { + private int ans; + private List[] g; + + public int countGoodNodes(int[][] edges) { + int n = edges.length + 1; + g = new List[n]; + Arrays.setAll(g, k -> new ArrayList<>()); + for (var e : edges) { + int a = e[0], b = e[1]; + g[a].add(b); + g[b].add(a); + } + dfs(0, -1); + return ans; + } + + private int dfs(int a, int fa) { + int pre = -1, cnt = 1, ok = 1; + for (int b : g[a]) { + if (b != fa) { + int cur = dfs(b, a); + cnt += cur; + if (pre < 0) { + pre = cur; + } else if (pre != cur) { + ok = 0; + } + } + } + ans += ok; + return cnt; + } +} +``` + +#### C++ + +```cpp +class Solution { +public: + int countGoodNodes(vector>& edges) { + int n = edges.size() + 1; + vector g[n]; + for (const auto& e : edges) { + int a = e[0], b = e[1]; + g[a].push_back(b); + g[b].push_back(a); + } + int ans = 0; + auto dfs = [&](auto&& dfs, int a, int fa) -> int { + int pre = -1, cnt = 1, ok = 1; + for (int b : g[a]) { + if (b != fa) { + int cur = dfs(dfs, b, a); + cnt += cur; + if (pre < 0) { + pre = cur; + } else if (pre != cur) { + ok = 0; + } + } + } + ans += ok; + return cnt; + }; + dfs(dfs, 0, -1); + return ans; + } +}; +``` + +#### Go + +```go +func countGoodNodes(edges [][]int) (ans int) { + n := len(edges) + 1 + g := make([][]int, n) + for _, e := range edges { + a, b := e[0], e[1] + g[a] = append(g[a], b) + g[b] = append(g[b], a) + } + var dfs func(int, int) int + dfs = func(a, fa int) int { + pre, cnt, ok := -1, 1, 1 + for _, b := range g[a] { + if b != fa { + cur := dfs(b, a) + cnt += cur + if pre < 0 { + pre = cur + } else if pre != cur { + ok = 0 + } + } + } + ans += ok + return cnt + } + dfs(0, -1) + return +} +``` + +#### TypeScript + +```ts +function countGoodNodes(edges: number[][]): number { + const n = edges.length + 1; + const g: number[][] = Array.from({ length: n }, () => []); + for (const [a, b] of edges) { + g[a].push(b); + g[b].push(a); + } + let ans = 0; + const dfs = (a: number, fa: number): number => { + let [pre, cnt, ok] = [-1, 1, 1]; + for (const b of g[a]) { + if (b !== fa) { + const cur = dfs(b, a); + cnt += cur; + if (pre < 0) { + pre = cur; + } else if (pre !== cur) { + ok = 0; + } + } + } + ans += ok; + return cnt; + }; + dfs(0, -1); + return ans; +} +``` + + + + + + diff --git a/solution/3200-3299/3249.Count the Number of Good Nodes/README_EN.md b/solution/3200-3299/3249.Count the Number of Good Nodes/README_EN.md new file mode 100644 index 0000000000000..b251ba71f7c7c --- /dev/null +++ b/solution/3200-3299/3249.Count the Number of Good Nodes/README_EN.md @@ -0,0 +1,270 @@ +--- +comments: true +difficulty: Medium +edit_url: https://github.com/doocs/leetcode/edit/main/solution/3200-3299/3249.Count%20the%20Number%20of%20Good%20Nodes/README_EN.md +--- + + + +# [3249. Count the Number of Good Nodes](https://leetcode.com/problems/count-the-number-of-good-nodes) + +[中文文档](/solution/3200-3299/3249.Count%20the%20Number%20of%20Good%20Nodes/README.md) + +## Description + + + +

There is an undirected tree with n nodes labeled from 0 to n - 1, and rooted at node 0. You are given a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

+ +

A node is good if all the subtrees rooted at its children have the same size.

+ +

Return the number of good nodes in the given tree.

+ +

A subtree of treeName is a tree consisting of a node in treeName and all of its descendants.

+ +

 

+

Example 1:

+ +
+

Input: edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]

+ +

Output: 7

+ +

Explanation:

+ +

All of the nodes of the given tree are good.

+
+ +

Example 2:

+ +
+

Input: edges = [[0,1],[1,2],[2,3],[3,4],[0,5],[1,6],[2,7],[3,8]]

+ +

Output: 6

+ +

Explanation:

+ +

There are 6 good nodes in the given tree. They are colored in the image above.

+ +

Example 3:

+ +
+

Input: edges = [[0,1],[1,2],[1,3],[1,4],[0,5],[5,6],[6,7],[7,8],[0,9],[9,10],[9,12],[10,11]]

+ +

Output: 12

+ +

Explanation:

+ +

All nodes except node 9 are good.

+
+
+ +

 

+

Constraints:

+ +
    +
  • 2 <= n <= 105
    • +
  • edges.length == n - 1
    • +
  • edges[i].length == 2
    • +
  • 0 <= ai, bi < n
    • +
  • The input is generated such that edges represents a valid tree.
    • +
+ + + +## Solutions + + + +### Solution 1: DFS + +First, we construct the adjacency list $\textit{g}$ of the tree based on the given edges $\textit{edges}$, where $\textit{g}[a]$ represents all the neighboring nodes of node $a$. + +Next, we design a function $\textit{dfs}(a, \textit{fa})$ to calculate the number of nodes in the subtree rooted at node $a$ and to accumulate the count of good nodes. Here, $\textit{fa}$ represents the parent node of node $a$. + +The execution process of the function $\textit{dfs}(a, \textit{fa})$ is as follows: + +1. Initialize variables $\textit{pre} = -1$, $\textit{cnt} = 1$, $\textit{ok} = 1$, representing the number of nodes in a subtree of node $a$, the total number of nodes in all subtrees of node $a$, and whether node $a$ is a good node, respectively. +2. Traverse all neighboring nodes $b$ of node $a$. If $b$ is not equal to $\textit{fa}$, recursively call $\textit{dfs}(b, a)$, with the return value being $\textit{cur}$, and add $\textit{cur}$ to $\textit{cnt}$. If $\textit{pre} < 0$, assign $\textit{cur}$ to $\textit{pre}$; otherwise, if $\textit{pre}$ is not equal to $\textit{cur}$, it means the number of nodes in different subtrees of node $a$ is different, and set $\textit{ok}$ to $0$. +3. Finally, add $\textit{ok}$ to the answer and return $\textit{cnt}$. + +In the main function, we call $\textit{dfs}(0, -1)$ and return the final answer. + +The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ represents the number of nodes. + + + +#### Python3 + +```python +class Solution: + def countGoodNodes(self, edges: List[List[int]]) -> int: + def dfs(a: int, fa: int) -> int: + pre = -1 + cnt = ok = 1 + for b in g[a]: + if b != fa: + cur = dfs(b, a) + cnt += cur + if pre < 0: + pre = cur + elif pre != cur: + ok = 0 + nonlocal ans + ans += ok + return cnt + + g = defaultdict(list) + for a, b in edges: + g[a].append(b) + g[b].append(a) + ans = 0 + dfs(0, -1) + return ans +``` + +#### Java + +```java +class Solution { + private int ans; + private List[] g; + + public int countGoodNodes(int[][] edges) { + int n = edges.length + 1; + g = new List[n]; + Arrays.setAll(g, k -> new ArrayList<>()); + for (var e : edges) { + int a = e[0], b = e[1]; + g[a].add(b); + g[b].add(a); + } + dfs(0, -1); + return ans; + } + + private int dfs(int a, int fa) { + int pre = -1, cnt = 1, ok = 1; + for (int b : g[a]) { + if (b != fa) { + int cur = dfs(b, a); + cnt += cur; + if (pre < 0) { + pre = cur; + } else if (pre != cur) { + ok = 0; + } + } + } + ans += ok; + return cnt; + } +} +``` + +#### C++ + +```cpp +class Solution { +public: + int countGoodNodes(vector>& edges) { + int n = edges.size() + 1; + vector g[n]; + for (const auto& e : edges) { + int a = e[0], b = e[1]; + g[a].push_back(b); + g[b].push_back(a); + } + int ans = 0; + auto dfs = [&](auto&& dfs, int a, int fa) -> int { + int pre = -1, cnt = 1, ok = 1; + for (int b : g[a]) { + if (b != fa) { + int cur = dfs(dfs, b, a); + cnt += cur; + if (pre < 0) { + pre = cur; + } else if (pre != cur) { + ok = 0; + } + } + } + ans += ok; + return cnt; + }; + dfs(dfs, 0, -1); + return ans; + } +}; +``` + +#### Go + +```go +func countGoodNodes(edges [][]int) (ans int) { + n := len(edges) + 1 + g := make([][]int, n) + for _, e := range edges { + a, b := e[0], e[1] + g[a] = append(g[a], b) + g[b] = append(g[b], a) + } + var dfs func(int, int) int + dfs = func(a, fa int) int { + pre, cnt, ok := -1, 1, 1 + for _, b := range g[a] { + if b != fa { + cur := dfs(b, a) + cnt += cur + if pre < 0 { + pre = cur + } else if pre != cur { + ok = 0 + } + } + } + ans += ok + return cnt + } + dfs(0, -1) + return +} +``` + +#### TypeScript + +```ts +function countGoodNodes(edges: number[][]): number { + const n = edges.length + 1; + const g: number[][] = Array.from({ length: n }, () => []); + for (const [a, b] of edges) { + g[a].push(b); + g[b].push(a); + } + let ans = 0; + const dfs = (a: number, fa: number): number => { + let [pre, cnt, ok] = [-1, 1, 1]; + for (const b of g[a]) { + if (b !== fa) { + const cur = dfs(b, a); + cnt += cur; + if (pre < 0) { + pre = cur; + } else if (pre !== cur) { + ok = 0; + } + } + } + ans += ok; + return cnt; + }; + dfs(0, -1); + return ans; +} +``` + + + + + + diff --git a/solution/3200-3299/3249.Count the Number of Good Nodes/Solution.cpp b/solution/3200-3299/3249.Count the Number of Good Nodes/Solution.cpp new file mode 100644 index 0000000000000..73189db599497 --- /dev/null +++ b/solution/3200-3299/3249.Count the Number of Good Nodes/Solution.cpp @@ -0,0 +1,31 @@ +class Solution { +public: + int countGoodNodes(vector>& edges) { + int n = edges.size() + 1; + vector g[n]; + for (const auto& e : edges) { + int a = e[0], b = e[1]; + g[a].push_back(b); + g[b].push_back(a); + } + int ans = 0; + auto dfs = [&](auto&& dfs, int a, int fa) -> int { + int pre = -1, cnt = 1, ok = 1; + for (int b : g[a]) { + if (b != fa) { + int cur = dfs(dfs, b, a); + cnt += cur; + if (pre < 0) { + pre = cur; + } else if (pre != cur) { + ok = 0; + } + } + } + ans += ok; + return cnt; + }; + dfs(dfs, 0, -1); + return ans; + } +}; diff --git a/solution/3200-3299/3249.Count the Number of Good Nodes/Solution.go b/solution/3200-3299/3249.Count the Number of Good Nodes/Solution.go new file mode 100644 index 0000000000000..fe5bc40195bd4 --- /dev/null +++ b/solution/3200-3299/3249.Count the Number of Good Nodes/Solution.go @@ -0,0 +1,28 @@ +func countGoodNodes(edges [][]int) (ans int) { + n := len(edges) + 1 + g := make([][]int, n) + for _, e := range edges { + a, b := e[0], e[1] + g[a] = append(g[a], b) + g[b] = append(g[b], a) + } + var dfs func(int, int) int + dfs = func(a, fa int) int { + pre, cnt, ok := -1, 1, 1 + for _, b := range g[a] { + if b != fa { + cur := dfs(b, a) + cnt += cur + if pre < 0 { + pre = cur + } else if pre != cur { + ok = 0 + } + } + } + ans += ok + return cnt + } + dfs(0, -1) + return +} diff --git a/solution/3200-3299/3249.Count the Number of Good Nodes/Solution.java b/solution/3200-3299/3249.Count the Number of Good Nodes/Solution.java new file mode 100644 index 0000000000000..3917be07c689b --- /dev/null +++ b/solution/3200-3299/3249.Count the Number of Good Nodes/Solution.java @@ -0,0 +1,34 @@ +class Solution { + private int ans; + private List[] g; + + public int countGoodNodes(int[][] edges) { + int n = edges.length + 1; + g = new List[n]; + Arrays.setAll(g, k -> new ArrayList<>()); + for (var e : edges) { + int a = e[0], b = e[1]; + g[a].add(b); + g[b].add(a); + } + dfs(0, -1); + return ans; + } + + private int dfs(int a, int fa) { + int pre = -1, cnt = 1, ok = 1; + for (int b : g[a]) { + if (b != fa) { + int cur = dfs(b, a); + cnt += cur; + if (pre < 0) { + pre = cur; + } else if (pre != cur) { + ok = 0; + } + } + } + ans += ok; + return cnt; + } +} diff --git a/solution/3200-3299/3249.Count the Number of Good Nodes/Solution.py b/solution/3200-3299/3249.Count the Number of Good Nodes/Solution.py new file mode 100644 index 0000000000000..035ca6e74663e --- /dev/null +++ b/solution/3200-3299/3249.Count the Number of Good Nodes/Solution.py @@ -0,0 +1,24 @@ +class Solution: + def countGoodNodes(self, edges: List[List[int]]) -> int: + def dfs(a: int, fa: int) -> int: + pre = -1 + cnt = ok = 1 + for b in g[a]: + if b != fa: + cur = dfs(b, a) + cnt += cur + if pre < 0: + pre = cur + elif pre != cur: + ok = 0 + nonlocal ans + ans += ok + return cnt + + g = defaultdict(list) + for a, b in edges: + g[a].append(b) + g[b].append(a) + ans = 0 + dfs(0, -1) + return ans diff --git a/solution/3200-3299/3249.Count the Number of Good Nodes/Solution.ts b/solution/3200-3299/3249.Count the Number of Good Nodes/Solution.ts new file mode 100644 index 0000000000000..adfc1f2b20d39 --- /dev/null +++ b/solution/3200-3299/3249.Count the Number of Good Nodes/Solution.ts @@ -0,0 +1,27 @@ +function countGoodNodes(edges: number[][]): number { + const n = edges.length + 1; + const g: number[][] = Array.from({ length: n }, () => []); + for (const [a, b] of edges) { + g[a].push(b); + g[b].push(a); + } + let ans = 0; + const dfs = (a: number, fa: number): number => { + let [pre, cnt, ok] = [-1, 1, 1]; + for (const b of g[a]) { + if (b !== fa) { + const cur = dfs(b, a); + cnt += cur; + if (pre < 0) { + pre = cur; + } else if (pre !== cur) { + ok = 0; + } + } + } + ans += ok; + return cnt; + }; + dfs(0, -1); + return ans; +} diff --git a/solution/3200-3299/3249.Count the Number of Good Nodes/images/rob.jpg b/solution/3200-3299/3249.Count the Number of Good Nodes/images/rob.jpg new file mode 100644 index 0000000000000..78cf21ae7bac5 Binary files /dev/null and b/solution/3200-3299/3249.Count the Number of Good Nodes/images/rob.jpg differ diff --git a/solution/3200-3299/3249.Count the Number of Good Nodes/images/screenshot-2024-06-03-193552.png b/solution/3200-3299/3249.Count the Number of Good Nodes/images/screenshot-2024-06-03-193552.png new file mode 100644 index 0000000000000..1a4674f03a9fb Binary files /dev/null and b/solution/3200-3299/3249.Count the Number of Good Nodes/images/screenshot-2024-06-03-193552.png differ diff --git a/solution/3200-3299/3249.Count the Number of Good Nodes/images/tree1.png b/solution/3200-3299/3249.Count the Number of Good Nodes/images/tree1.png new file mode 100644 index 0000000000000..aa41918f80818 Binary files /dev/null and b/solution/3200-3299/3249.Count the Number of Good Nodes/images/tree1.png differ diff --git a/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/README.md b/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/README.md new file mode 100644 index 0000000000000..fb312a499e1b8 --- /dev/null +++ b/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/README.md @@ -0,0 +1,248 @@ +--- +comments: true +difficulty: 困难 +edit_url: https://github.com/doocs/leetcode/edit/main/solution/3200-3299/3250.Find%20the%20Count%20of%20Monotonic%20Pairs%20I/README.md +--- + + + +# [3250. 单调数组对的数目 I](https://leetcode.cn/problems/find-the-count-of-monotonic-pairs-i) + +[English Version](/solution/3200-3299/3250.Find%20the%20Count%20of%20Monotonic%20Pairs%20I/README_EN.md) + +## 题目描述 + + + +

给你一个长度为 n 的 正 整数数组 nums 。

+ +

如果两个 非负 整数数组 (arr1, arr2) 满足以下条件，我们称它们是 单调 数组对：

+ +
    +
  • 两个数组的长度都是 n 。
    • +
  • arr1 是单调 非递减 的，换句话说 arr1[0] <= arr1[1] <= ... <= arr1[n - 1] 。
    • +
  • arr2 是单调 非递增 的，换句话说 arr2[0] >= arr2[1] >= ... >= arr2[n - 1] 。
    • +
  • 对于所有的 0 <= i <= n - 1 都有 arr1[i] + arr2[i] == nums[i] 。
    • +
+ +

请你返回所有 单调 数组对的数目。

+ +

由于答案可能很大，请你将它对 109 + 7 取余 后返回。

+ +

 

+ +

示例 1：

+ +
+

输入：nums = [2,3,2]

+ +

输出：4

+ +

解释：

+ +

单调数组对包括：

+ +
    +
  1. ([0, 1, 1], [2, 2, 1])
    2. +
  2. ([0, 1, 2], [2, 2, 0])
    3. +
  3. ([0, 2, 2], [2, 1, 0])
    4. +
  4. ([1, 2, 2], [1, 1, 0])
    5. +
+
+ +

示例 2：

+ +
+

输入：nums = [5,5,5,5]

+ +

输出：126

+
+ +

 

+ +

提示：

+ +
    +
  • 1 <= n == nums.length <= 2000
    • +
  • 1 <= nums[i] <= 50
    • +
+ + + +## 解法 + + + +### 方法一：动态规划 + 前缀和优化 + +我们定义 $f[i][j]$ 表示下标 $[0,..i]$ 的单调数组对的数目，且 $arr1[i] = j$。初始时 $[i][j] = 0$，答案为 $\sum_{j=0}^{\textit{nums}[n-1]} f[n-1][j]$。 + +当 $i = 0$ 时，有 $[0][j] = 1$，其中 $0 \leq j \leq \textit{nums}[0]$。 + +当 $i > 0$ 时，我们可以根据 $f[i-1][j']$ 计算 $f[i][j]$。由于 $\textit{arr1}$ 是单调非递减的，因此 $j' \leq j$。又由于 $\textit{arr2}$ 是单调非递增的，因此 $\textit{nums}[i] - j \leq \textit{nums}[i - 1] - j'$。即 $j' \leq \min(j, j + \textit{nums}[i - 1] - \textit{nums}[i])$。 + +答案为 $\sum_{j=0}^{\textit{nums}[n-1]} f[n-1][j]$。 + +时间复杂度 $O(n \times m)$，空间复杂度 $O(n \times m)$。其中 $n$ 表示数组 $\textit{nums}$ 的长度，而 $m$ 表示数组 $\textit{nums}$ 中的最大值。 + + + +#### Python3 + +```python +class Solution: + def countOfPairs(self, nums: List[int]) -> int: + mod = 10**9 + 7 + n, m = len(nums), max(nums) + f = [[0] * (m + 1) for _ in range(n)] + for j in range(nums[0] + 1): + f[0][j] = 1 + for i in range(1, n): + s = list(accumulate(f[i - 1])) + for j in range(nums[i] + 1): + k = min(j, j + nums[i - 1] - nums[i]) + if k >= 0: + f[i][j] = s[k] % mod + return sum(f[-1][: nums[-1] + 1]) % mod +``` + +#### Java + +```java +class Solution { + public int countOfPairs(int[] nums) { + final int mod = (int) 1e9 + 7; + int n = nums.length; + int m = Arrays.stream(nums).max().getAsInt(); + int[][] f = new int[n][m + 1]; + for (int j = 0; j <= nums[0]; ++j) { + f[0][j] = 1; + } + int[] g = new int[m + 1]; + for (int i = 1; i < n; ++i) { + g[0] = f[i - 1][0]; + for (int j = 1; j <= m; ++j) { + g[j] = (g[j - 1] + f[i - 1][j]) % mod; + } + for (int j = 0; j <= nums[i]; ++j) { + int k = Math.min(j, j + nums[i - 1] - nums[i]); + if (k >= 0) { + f[i][j] = g[k]; + } + } + } + int ans = 0; + for (int j = 0; j <= nums[n - 1]; ++j) { + ans = (ans + f[n - 1][j]) % mod; + } + return ans; + } +} +``` + +#### C++ + +```cpp +class Solution { +public: + int countOfPairs(vector& nums) { + const int mod = 1e9 + 7; + int n = nums.size(); + int m = *max_element(nums.begin(), nums.end()); + vector> f(n, vector(m + 1)); + for (int j = 0; j <= nums[0]; ++j) { + f[0][j] = 1; + } + vector g(m + 1); + for (int i = 1; i < n; ++i) { + g[0] = f[i - 1][0]; + for (int j = 1; j <= m; ++j) { + g[j] = (g[j - 1] + f[i - 1][j]) % mod; + } + for (int j = 0; j <= nums[i]; ++j) { + int k = min(j, j + nums[i - 1] - nums[i]); + if (k >= 0) { + f[i][j] = g[k]; + } + } + } + int ans = 0; + for (int j = 0; j <= nums[n - 1]; ++j) { + ans = (ans + f[n - 1][j]) % mod; + } + return ans; + } +}; +``` + +#### Go + +```go +func countOfPairs(nums []int) (ans int) { + const mod int = 1e9 + 7 + n := len(nums) + m := slices.Max(nums) + f := make([][]int, n) + for i := range f { + f[i] = make([]int, m+1) + } + for j := 0; j <= nums[0]; j++ { + f[0][j] = 1 + } + g := make([]int, m+1) + for i := 1; i < n; i++ { + g[0] = f[i-1][0] + for j := 1; j <= m; j++ { + g[j] = (g[j-1] + f[i-1][j]) % mod + } + for j := 0; j <= nums[i]; j++ { + k := min(j, j+nums[i-1]-nums[i]) + if k >= 0 { + f[i][j] = g[k] + } + } + } + for j := 0; j <= nums[n-1]; j++ { + ans = (ans + f[n-1][j]) % mod + } + return +} +``` + +#### TypeScript + +```ts +function countOfPairs(nums: number[]): number { + const mod = 1e9 + 7; + const n = nums.length; + const m = Math.max(...nums); + const f: number[][] = Array.from({ length: n }, () => Array(m + 1).fill(0)); + for (let j = 0; j <= nums[0]; j++) { + f[0][j] = 1; + } + const g: number[] = Array(m + 1).fill(0); + for (let i = 1; i < n; i++) { + g[0] = f[i - 1][0]; + for (let j = 1; j <= m; j++) { + g[j] = (g[j - 1] + f[i - 1][j]) % mod; + } + for (let j = 0; j <= nums[i]; j++) { + const k = Math.min(j, j + nums[i - 1] - nums[i]); + if (k >= 0) { + f[i][j] = g[k]; + } + } + } + let ans = 0; + for (let j = 0; j <= nums[n - 1]; j++) { + ans = (ans + f[n - 1][j]) % mod; + } + return ans; +} +``` + + + + + + diff --git a/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/README_EN.md b/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/README_EN.md new file mode 100644 index 0000000000000..c01cde5beb182 --- /dev/null +++ b/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/README_EN.md @@ -0,0 +1,246 @@ +--- +comments: true +difficulty: Hard +edit_url: https://github.com/doocs/leetcode/edit/main/solution/3200-3299/3250.Find%20the%20Count%20of%20Monotonic%20Pairs%20I/README_EN.md +--- + + + +# [3250. Find the Count of Monotonic Pairs I](https://leetcode.com/problems/find-the-count-of-monotonic-pairs-i) + +[中文文档](/solution/3200-3299/3250.Find%20the%20Count%20of%20Monotonic%20Pairs%20I/README.md) + +## Description + + + +

You are given an array of positive integers nums of length n.

+ +

We call a pair of non-negative integer arrays (arr1, arr2) monotonic if:

+ +
    +
  • The lengths of both arrays are n.
    • +
  • arr1 is monotonically non-decreasing, in other words, arr1[0] <= arr1[1] <= ... <= arr1[n - 1].
    • +
  • arr2 is monotonically non-increasing, in other words, arr2[0] >= arr2[1] >= ... >= arr2[n - 1].
    • +
  • arr1[i] + arr2[i] == nums[i] for all 0 <= i <= n - 1.
    • +
+ +

Return the count of monotonic pairs.

+ +

Since the answer may be very large, return it modulo 109 + 7.

+ +

 

+

Example 1:

+ +
+

Input: nums = [2,3,2]

+ +

Output: 4

+ +

Explanation:

+ +

The good pairs are:

+ +
    +
  1. ([0, 1, 1], [2, 2, 1])
    2. +
  2. ([0, 1, 2], [2, 2, 0])
    3. +
  3. ([0, 2, 2], [2, 1, 0])
    4. +
  4. ([1, 2, 2], [1, 1, 0])
    5. +
+
+ +

Example 2:

+ +
+

Input: nums = [5,5,5,5]

+ +

Output: 126

+
+ +

 

+

Constraints:

+ +
    +
  • 1 <= n == nums.length <= 2000
    • +
  • 1 <= nums[i] <= 50
    • +
+ + + +## Solutions + + + +### Solution 1: Dynamic Programming + Prefix Sum Optimization + +We define $f[i][j]$ to represent the number of monotonic array pairs for the subarray $[0, \ldots, i]$ where $arr1[i] = j$. Initially, $f[i][j] = 0$, and the answer is $\sum_{j=0}^{\textit{nums}[n-1]} f[n-1][j]$. + +When $i = 0$, we have $f[0][j] = 1$ for $0 \leq j \leq \textit{nums}[0]$. + +When $i > 0$, we can calculate $f[i][j]$ based on $f[i-1][j']$. Since $\textit{arr1}$ is non-decreasing, $j' \leq j$. Additionally, since $\textit{arr2}$ is non-increasing, $\textit{nums}[i] - j \leq \textit{nums}[i - 1] - j'$. Thus, $j' \leq \min(j, j + \textit{nums}[i - 1] - \textit{nums}[i])$. + +The answer is $\sum_{j=0}^{\textit{nums}[n-1]} f[n-1][j]$. + +The time complexity is $O(n \times m)$, and the space complexity is $O(n \times m)$. Here, $n$ represents the length of the array $\textit{nums}$, and $m$ represents the maximum value in the array $\textit{nums}$. + + + +#### Python3 + +```python +class Solution: + def countOfPairs(self, nums: List[int]) -> int: + mod = 10**9 + 7 + n, m = len(nums), max(nums) + f = [[0] * (m + 1) for _ in range(n)] + for j in range(nums[0] + 1): + f[0][j] = 1 + for i in range(1, n): + s = list(accumulate(f[i - 1])) + for j in range(nums[i] + 1): + k = min(j, j + nums[i - 1] - nums[i]) + if k >= 0: + f[i][j] = s[k] % mod + return sum(f[-1][: nums[-1] + 1]) % mod +``` + +#### Java + +```java +class Solution { + public int countOfPairs(int[] nums) { + final int mod = (int) 1e9 + 7; + int n = nums.length; + int m = Arrays.stream(nums).max().getAsInt(); + int[][] f = new int[n][m + 1]; + for (int j = 0; j <= nums[0]; ++j) { + f[0][j] = 1; + } + int[] g = new int[m + 1]; + for (int i = 1; i < n; ++i) { + g[0] = f[i - 1][0]; + for (int j = 1; j <= m; ++j) { + g[j] = (g[j - 1] + f[i - 1][j]) % mod; + } + for (int j = 0; j <= nums[i]; ++j) { + int k = Math.min(j, j + nums[i - 1] - nums[i]); + if (k >= 0) { + f[i][j] = g[k]; + } + } + } + int ans = 0; + for (int j = 0; j <= nums[n - 1]; ++j) { + ans = (ans + f[n - 1][j]) % mod; + } + return ans; + } +} +``` + +#### C++ + +```cpp +class Solution { +public: + int countOfPairs(vector& nums) { + const int mod = 1e9 + 7; + int n = nums.size(); + int m = *max_element(nums.begin(), nums.end()); + vector> f(n, vector(m + 1)); + for (int j = 0; j <= nums[0]; ++j) { + f[0][j] = 1; + } + vector g(m + 1); + for (int i = 1; i < n; ++i) { + g[0] = f[i - 1][0]; + for (int j = 1; j <= m; ++j) { + g[j] = (g[j - 1] + f[i - 1][j]) % mod; + } + for (int j = 0; j <= nums[i]; ++j) { + int k = min(j, j + nums[i - 1] - nums[i]); + if (k >= 0) { + f[i][j] = g[k]; + } + } + } + int ans = 0; + for (int j = 0; j <= nums[n - 1]; ++j) { + ans = (ans + f[n - 1][j]) % mod; + } + return ans; + } +}; +``` + +#### Go + +```go +func countOfPairs(nums []int) (ans int) { + const mod int = 1e9 + 7 + n := len(nums) + m := slices.Max(nums) + f := make([][]int, n) + for i := range f { + f[i] = make([]int, m+1) + } + for j := 0; j <= nums[0]; j++ { + f[0][j] = 1 + } + g := make([]int, m+1) + for i := 1; i < n; i++ { + g[0] = f[i-1][0] + for j := 1; j <= m; j++ { + g[j] = (g[j-1] + f[i-1][j]) % mod + } + for j := 0; j <= nums[i]; j++ { + k := min(j, j+nums[i-1]-nums[i]) + if k >= 0 { + f[i][j] = g[k] + } + } + } + for j := 0; j <= nums[n-1]; j++ { + ans = (ans + f[n-1][j]) % mod + } + return +} +``` + +#### TypeScript + +```ts +function countOfPairs(nums: number[]): number { + const mod = 1e9 + 7; + const n = nums.length; + const m = Math.max(...nums); + const f: number[][] = Array.from({ length: n }, () => Array(m + 1).fill(0)); + for (let j = 0; j <= nums[0]; j++) { + f[0][j] = 1; + } + const g: number[] = Array(m + 1).fill(0); + for (let i = 1; i < n; i++) { + g[0] = f[i - 1][0]; + for (let j = 1; j <= m; j++) { + g[j] = (g[j - 1] + f[i - 1][j]) % mod; + } + for (let j = 0; j <= nums[i]; j++) { + const k = Math.min(j, j + nums[i - 1] - nums[i]); + if (k >= 0) { + f[i][j] = g[k]; + } + } + } + let ans = 0; + for (let j = 0; j <= nums[n - 1]; j++) { + ans = (ans + f[n - 1][j]) % mod; + } + return ans; +} +``` + + + + + + diff --git a/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/Solution.cpp b/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/Solution.cpp new file mode 100644 index 0000000000000..835f1154a7ade --- /dev/null +++ b/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/Solution.cpp @@ -0,0 +1,30 @@ +class Solution { +public: + int countOfPairs(vector& nums) { + const int mod = 1e9 + 7; + int n = nums.size(); + int m = *max_element(nums.begin(), nums.end()); + vector> f(n, vector(m + 1)); + for (int j = 0; j <= nums[0]; ++j) { + f[0][j] = 1; + } + vector g(m + 1); + for (int i = 1; i < n; ++i) { + g[0] = f[i - 1][0]; + for (int j = 1; j <= m; ++j) { + g[j] = (g[j - 1] + f[i - 1][j]) % mod; + } + for (int j = 0; j <= nums[i]; ++j) { + int k = min(j, j + nums[i - 1] - nums[i]); + if (k >= 0) { + f[i][j] = g[k]; + } + } + } + int ans = 0; + for (int j = 0; j <= nums[n - 1]; ++j) { + ans = (ans + f[n - 1][j]) % mod; + } + return ans; + } +}; diff --git a/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/Solution.go b/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/Solution.go new file mode 100644 index 0000000000000..72ed9c30e80f3 --- /dev/null +++ b/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/Solution.go @@ -0,0 +1,29 @@ +func countOfPairs(nums []int) (ans int) { + const mod int = 1e9 + 7 + n := len(nums) + m := slices.Max(nums) + f := make([][]int, n) + for i := range f { + f[i] = make([]int, m+1) + } + for j := 0; j <= nums[0]; j++ { + f[0][j] = 1 + } + g := make([]int, m+1) + for i := 1; i < n; i++ { + g[0] = f[i-1][0] + for j := 1; j <= m; j++ { + g[j] = (g[j-1] + f[i-1][j]) % mod + } + for j := 0; j <= nums[i]; j++ { + k := min(j, j+nums[i-1]-nums[i]) + if k >= 0 { + f[i][j] = g[k] + } + } + } + for j := 0; j <= nums[n-1]; j++ { + ans = (ans + f[n-1][j]) % mod + } + return +} diff --git a/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/Solution.java b/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/Solution.java new file mode 100644 index 0000000000000..6391ae1136ff4 --- /dev/null +++ b/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/Solution.java @@ -0,0 +1,29 @@ +class Solution { + public int countOfPairs(int[] nums) { + final int mod = (int) 1e9 + 7; + int n = nums.length; + int m = Arrays.stream(nums).max().getAsInt(); + int[][] f = new int[n][m + 1]; + for (int j = 0; j <= nums[0]; ++j) { + f[0][j] = 1; + } + int[] g = new int[m + 1]; + for (int i = 1; i < n; ++i) { + g[0] = f[i - 1][0]; + for (int j = 1; j <= m; ++j) { + g[j] = (g[j - 1] + f[i - 1][j]) % mod; + } + for (int j = 0; j <= nums[i]; ++j) { + int k = Math.min(j, j + nums[i - 1] - nums[i]); + if (k >= 0) { + f[i][j] = g[k]; + } + } + } + int ans = 0; + for (int j = 0; j <= nums[n - 1]; ++j) { + ans = (ans + f[n - 1][j]) % mod; + } + return ans; + } +} diff --git a/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/Solution.py b/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/Solution.py new file mode 100644 index 0000000000000..cf4957154bf61 --- /dev/null +++ b/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/Solution.py @@ -0,0 +1,14 @@ +class Solution: + def countOfPairs(self, nums: List[int]) -> int: + mod = 10**9 + 7 + n, m = len(nums), max(nums) + f = [[0] * (m + 1) for _ in range(n)] + for j in range(nums[0] + 1): + f[0][j] = 1 + for i in range(1, n): + s = list(accumulate(f[i - 1])) + for j in range(nums[i] + 1): + k = min(j, j + nums[i - 1] - nums[i]) + if k >= 0: + f[i][j] = s[k] % mod + return sum(f[-1][: nums[-1] + 1]) % mod diff --git a/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/Solution.ts b/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/Solution.ts new file mode 100644 index 0000000000000..94b14790bc2e3 --- /dev/null +++ b/solution/3200-3299/3250.Find the Count of Monotonic Pairs I/Solution.ts @@ -0,0 +1,27 @@ +function countOfPairs(nums: number[]): number { + const mod = 1e9 + 7; + const n = nums.length; + const m = Math.max(...nums); + const f: number[][] = Array.from({ length: n }, () => Array(m + 1).fill(0)); + for (let j = 0; j <= nums[0]; j++) { + f[0][j] = 1; + } + const g: number[] = Array(m + 1).fill(0); + for (let i = 1; i < n; i++) { + g[0] = f[i - 1][0]; + for (let j = 1; j <= m; j++) { + g[j] = (g[j - 1] + f[i - 1][j]) % mod; + } + for (let j = 0; j <= nums[i]; j++) { + const k = Math.min(j, j + nums[i - 1] - nums[i]); + if (k >= 0) { + f[i][j] = g[k]; + } + } + } + let ans = 0; + for (let j = 0; j <= nums[n - 1]; j++) { + ans = (ans + f[n - 1][j]) % mod; + } + return ans; +} diff --git a/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/README.md b/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/README.md new file mode 100644 index 0000000000000..c1156c4d1d1cf --- /dev/null +++ b/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/README.md @@ -0,0 +1,248 @@ +--- +comments: true +difficulty: 困难 +edit_url: https://github.com/doocs/leetcode/edit/main/solution/3200-3299/3251.Find%20the%20Count%20of%20Monotonic%20Pairs%20II/README.md +--- + + + +# [3251. 单调数组对的数目 II](https://leetcode.cn/problems/find-the-count-of-monotonic-pairs-ii) + +[English Version](/solution/3200-3299/3251.Find%20the%20Count%20of%20Monotonic%20Pairs%20II/README_EN.md) + +## 题目描述 + + + +

给你一个长度为 n 的 正 整数数组 nums 。

+ +

如果两个 非负 整数数组 (arr1, arr2) 满足以下条件，我们称它们是 单调 数组对：

+ +
    +
  • 两个数组的长度都是 n 。
    • +
  • arr1 是单调 非递减 的，换句话说 arr1[0] <= arr1[1] <= ... <= arr1[n - 1] 。
    • +
  • arr2 是单调 非递增 的，换句话说 arr2[0] >= arr2[1] >= ... >= arr2[n - 1] 。
    • +
  • 对于所有的 0 <= i <= n - 1 都有 arr1[i] + arr2[i] == nums[i] 。
    • +
+ +

请你返回所有 单调 数组对的数目。

+ +

由于答案可能很大，请你将它对 109 + 7 取余 后返回。

+ +

 

+ +

示例 1：

+ +
+

输入：nums = [2,3,2]

+ +

输出：4

+ +

解释：

+ +

单调数组对包括：

+ +
    +
  1. ([0, 1, 1], [2, 2, 1])
    2. +
  2. ([0, 1, 2], [2, 2, 0])
    3. +
  3. ([0, 2, 2], [2, 1, 0])
    4. +
  4. ([1, 2, 2], [1, 1, 0])
    5. +
+
+ +

示例 2：

+ +
+

输入：nums = [5,5,5,5]

+ +

输出：126

+
+ +

 

+ +

提示：

+ +
    +
  • 1 <= n == nums.length <= 2000
    • +
  • 1 <= nums[i] <= 1000
    • +
+ + + +## 解法 + + + +### 方法一：动态规划 + 前缀和优化 + +我们定义 $f[i][j]$ 表示下标 $[0,..i]$ 的单调数组对的数目，且 $arr1[i] = j$。初始时 $[i][j] = 0$，答案为 $\sum_{j=0}^{\textit{nums}[n-1]} f[n-1][j]$。 + +当 $i = 0$ 时，有 $[0][j] = 1$，其中 $0 \leq j \leq \textit{nums}[0]$。 + +当 $i > 0$ 时，我们可以根据 $f[i-1][j']$ 计算 $f[i][j]$。由于 $\textit{arr1}$ 是单调非递减的，因此 $j' \leq j$。又由于 $\textit{arr2}$ 是单调非递增的，因此 $\textit{nums}[i] - j \leq \textit{nums}[i - 1] - j'$。即 $j' \leq \min(j, j + \textit{nums}[i - 1] - \textit{nums}[i])$。 + +答案为 $\sum_{j=0}^{\textit{nums}[n-1]} f[n-1][j]$。 + +时间复杂度 $O(n \times m)$，空间复杂度 $O(n \times m)$。其中 $n$ 表示数组 $\textit{nums}$ 的长度，而 $m$ 表示数组 $\textit{nums}$ 中的最大值。 + + + +#### Python3 + +```python +class Solution: + def countOfPairs(self, nums: List[int]) -> int: + mod = 10**9 + 7 + n, m = len(nums), max(nums) + f = [[0] * (m + 1) for _ in range(n)] + for j in range(nums[0] + 1): + f[0][j] = 1 + for i in range(1, n): + s = list(accumulate(f[i - 1])) + for j in range(nums[i] + 1): + k = min(j, j + nums[i - 1] - nums[i]) + if k >= 0: + f[i][j] = s[k] % mod + return sum(f[-1][: nums[-1] + 1]) % mod +``` + +#### Java + +```java +class Solution { + public int countOfPairs(int[] nums) { + final int mod = (int) 1e9 + 7; + int n = nums.length; + int m = Arrays.stream(nums).max().getAsInt(); + int[][] f = new int[n][m + 1]; + for (int j = 0; j <= nums[0]; ++j) { + f[0][j] = 1; + } + int[] g = new int[m + 1]; + for (int i = 1; i < n; ++i) { + g[0] = f[i - 1][0]; + for (int j = 1; j <= m; ++j) { + g[j] = (g[j - 1] + f[i - 1][j]) % mod; + } + for (int j = 0; j <= nums[i]; ++j) { + int k = Math.min(j, j + nums[i - 1] - nums[i]); + if (k >= 0) { + f[i][j] = g[k]; + } + } + } + int ans = 0; + for (int j = 0; j <= nums[n - 1]; ++j) { + ans = (ans + f[n - 1][j]) % mod; + } + return ans; + } +} +``` + +#### C++ + +```cpp +class Solution { +public: + int countOfPairs(vector& nums) { + const int mod = 1e9 + 7; + int n = nums.size(); + int m = *max_element(nums.begin(), nums.end()); + vector> f(n, vector(m + 1)); + for (int j = 0; j <= nums[0]; ++j) { + f[0][j] = 1; + } + vector g(m + 1); + for (int i = 1; i < n; ++i) { + g[0] = f[i - 1][0]; + for (int j = 1; j <= m; ++j) { + g[j] = (g[j - 1] + f[i - 1][j]) % mod; + } + for (int j = 0; j <= nums[i]; ++j) { + int k = min(j, j + nums[i - 1] - nums[i]); + if (k >= 0) { + f[i][j] = g[k]; + } + } + } + int ans = 0; + for (int j = 0; j <= nums[n - 1]; ++j) { + ans = (ans + f[n - 1][j]) % mod; + } + return ans; + } +}; +``` + +#### Go + +```go +func countOfPairs(nums []int) (ans int) { + const mod int = 1e9 + 7 + n := len(nums) + m := slices.Max(nums) + f := make([][]int, n) + for i := range f { + f[i] = make([]int, m+1) + } + for j := 0; j <= nums[0]; j++ { + f[0][j] = 1 + } + g := make([]int, m+1) + for i := 1; i < n; i++ { + g[0] = f[i-1][0] + for j := 1; j <= m; j++ { + g[j] = (g[j-1] + f[i-1][j]) % mod + } + for j := 0; j <= nums[i]; j++ { + k := min(j, j+nums[i-1]-nums[i]) + if k >= 0 { + f[i][j] = g[k] + } + } + } + for j := 0; j <= nums[n-1]; j++ { + ans = (ans + f[n-1][j]) % mod + } + return +} +``` + +#### TypeScript + +```ts +function countOfPairs(nums: number[]): number { + const mod = 1e9 + 7; + const n = nums.length; + const m = Math.max(...nums); + const f: number[][] = Array.from({ length: n }, () => Array(m + 1).fill(0)); + for (let j = 0; j <= nums[0]; j++) { + f[0][j] = 1; + } + const g: number[] = Array(m + 1).fill(0); + for (let i = 1; i < n; i++) { + g[0] = f[i - 1][0]; + for (let j = 1; j <= m; j++) { + g[j] = (g[j - 1] + f[i - 1][j]) % mod; + } + for (let j = 0; j <= nums[i]; j++) { + const k = Math.min(j, j + nums[i - 1] - nums[i]); + if (k >= 0) { + f[i][j] = g[k]; + } + } + } + let ans = 0; + for (let j = 0; j <= nums[n - 1]; j++) { + ans = (ans + f[n - 1][j]) % mod; + } + return ans; +} +``` + + + + + + diff --git a/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/README_EN.md b/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/README_EN.md new file mode 100644 index 0000000000000..749b4f2cc9d23 --- /dev/null +++ b/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/README_EN.md @@ -0,0 +1,246 @@ +--- +comments: true +difficulty: Hard +edit_url: https://github.com/doocs/leetcode/edit/main/solution/3200-3299/3251.Find%20the%20Count%20of%20Monotonic%20Pairs%20II/README_EN.md +--- + + + +# [3251. Find the Count of Monotonic Pairs II](https://leetcode.com/problems/find-the-count-of-monotonic-pairs-ii) + +[中文文档](/solution/3200-3299/3251.Find%20the%20Count%20of%20Monotonic%20Pairs%20II/README.md) + +## Description + + + +

You are given an array of positive integers nums of length n.

+ +

We call a pair of non-negative integer arrays (arr1, arr2) monotonic if:

+ +
    +
  • The lengths of both arrays are n.
    • +
  • arr1 is monotonically non-decreasing, in other words, arr1[0] <= arr1[1] <= ... <= arr1[n - 1].
    • +
  • arr2 is monotonically non-increasing, in other words, arr2[0] >= arr2[1] >= ... >= arr2[n - 1].
    • +
  • arr1[i] + arr2[i] == nums[i] for all 0 <= i <= n - 1.
    • +
+ +

Return the count of monotonic pairs.

+ +

Since the answer may be very large, return it modulo 109 + 7.

+ +

 

+

Example 1:

+ +
+

Input: nums = [2,3,2]

+ +

Output: 4

+ +

Explanation:

+ +

The good pairs are:

+ +
    +
  1. ([0, 1, 1], [2, 2, 1])
    2. +
  2. ([0, 1, 2], [2, 2, 0])
    3. +
  3. ([0, 2, 2], [2, 1, 0])
    4. +
  4. ([1, 2, 2], [1, 1, 0])
    5. +
+
+ +

Example 2:

+ +
+

Input: nums = [5,5,5,5]

+ +

Output: 126

+
+ +

 

+

Constraints:

+ +
    +
  • 1 <= n == nums.length <= 2000
    • +
  • 1 <= nums[i] <= 1000
    • +
+ + + +## Solutions + + + +### Solution 1: Dynamic Programming + Prefix Sum Optimization + +We define $f[i][j]$ to represent the number of monotonic array pairs for the subarray $[0, \ldots, i]$ where $arr1[i] = j$. Initially, $f[i][j] = 0$, and the answer is $\sum_{j=0}^{\textit{nums}[n-1]} f[n-1][j]$. + +When $i = 0$, we have $f[0][j] = 1$ for $0 \leq j \leq \textit{nums}[0]$. + +When $i > 0$, we can calculate $f[i][j]$ based on $f[i-1][j']$. Since $\textit{arr1}$ is non-decreasing, $j' \leq j$. Additionally, since $\textit{arr2}$ is non-increasing, $\textit{nums}[i] - j \leq \textit{nums}[i - 1] - j'$. Thus, $j' \leq \min(j, j + \textit{nums}[i - 1] - \textit{nums}[i])$. + +The answer is $\sum_{j=0}^{\textit{nums}[n-1]} f[n-1][j]$. + +The time complexity is $O(n \times m)$, and the space complexity is $O(n \times m)$. Here, $n$ represents the length of the array $\textit{nums}$, and $m$ represents the maximum value in the array $\textit{nums}$. + + + +#### Python3 + +```python +class Solution: + def countOfPairs(self, nums: List[int]) -> int: + mod = 10**9 + 7 + n, m = len(nums), max(nums) + f = [[0] * (m + 1) for _ in range(n)] + for j in range(nums[0] + 1): + f[0][j] = 1 + for i in range(1, n): + s = list(accumulate(f[i - 1])) + for j in range(nums[i] + 1): + k = min(j, j + nums[i - 1] - nums[i]) + if k >= 0: + f[i][j] = s[k] % mod + return sum(f[-1][: nums[-1] + 1]) % mod +``` + +#### Java + +```java +class Solution { + public int countOfPairs(int[] nums) { + final int mod = (int) 1e9 + 7; + int n = nums.length; + int m = Arrays.stream(nums).max().getAsInt(); + int[][] f = new int[n][m + 1]; + for (int j = 0; j <= nums[0]; ++j) { + f[0][j] = 1; + } + int[] g = new int[m + 1]; + for (int i = 1; i < n; ++i) { + g[0] = f[i - 1][0]; + for (int j = 1; j <= m; ++j) { + g[j] = (g[j - 1] + f[i - 1][j]) % mod; + } + for (int j = 0; j <= nums[i]; ++j) { + int k = Math.min(j, j + nums[i - 1] - nums[i]); + if (k >= 0) { + f[i][j] = g[k]; + } + } + } + int ans = 0; + for (int j = 0; j <= nums[n - 1]; ++j) { + ans = (ans + f[n - 1][j]) % mod; + } + return ans; + } +} +``` + +#### C++ + +```cpp +class Solution { +public: + int countOfPairs(vector& nums) { + const int mod = 1e9 + 7; + int n = nums.size(); + int m = *max_element(nums.begin(), nums.end()); + vector> f(n, vector(m + 1)); + for (int j = 0; j <= nums[0]; ++j) { + f[0][j] = 1; + } + vector g(m + 1); + for (int i = 1; i < n; ++i) { + g[0] = f[i - 1][0]; + for (int j = 1; j <= m; ++j) { + g[j] = (g[j - 1] + f[i - 1][j]) % mod; + } + for (int j = 0; j <= nums[i]; ++j) { + int k = min(j, j + nums[i - 1] - nums[i]); + if (k >= 0) { + f[i][j] = g[k]; + } + } + } + int ans = 0; + for (int j = 0; j <= nums[n - 1]; ++j) { + ans = (ans + f[n - 1][j]) % mod; + } + return ans; + } +}; +``` + +#### Go + +```go +func countOfPairs(nums []int) (ans int) { + const mod int = 1e9 + 7 + n := len(nums) + m := slices.Max(nums) + f := make([][]int, n) + for i := range f { + f[i] = make([]int, m+1) + } + for j := 0; j <= nums[0]; j++ { + f[0][j] = 1 + } + g := make([]int, m+1) + for i := 1; i < n; i++ { + g[0] = f[i-1][0] + for j := 1; j <= m; j++ { + g[j] = (g[j-1] + f[i-1][j]) % mod + } + for j := 0; j <= nums[i]; j++ { + k := min(j, j+nums[i-1]-nums[i]) + if k >= 0 { + f[i][j] = g[k] + } + } + } + for j := 0; j <= nums[n-1]; j++ { + ans = (ans + f[n-1][j]) % mod + } + return +} +``` + +#### TypeScript + +```ts +function countOfPairs(nums: number[]): number { + const mod = 1e9 + 7; + const n = nums.length; + const m = Math.max(...nums); + const f: number[][] = Array.from({ length: n }, () => Array(m + 1).fill(0)); + for (let j = 0; j <= nums[0]; j++) { + f[0][j] = 1; + } + const g: number[] = Array(m + 1).fill(0); + for (let i = 1; i < n; i++) { + g[0] = f[i - 1][0]; + for (let j = 1; j <= m; j++) { + g[j] = (g[j - 1] + f[i - 1][j]) % mod; + } + for (let j = 0; j <= nums[i]; j++) { + const k = Math.min(j, j + nums[i - 1] - nums[i]); + if (k >= 0) { + f[i][j] = g[k]; + } + } + } + let ans = 0; + for (let j = 0; j <= nums[n - 1]; j++) { + ans = (ans + f[n - 1][j]) % mod; + } + return ans; +} +``` + + + + + + diff --git a/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/Solution.cpp b/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/Solution.cpp new file mode 100644 index 0000000000000..835f1154a7ade --- /dev/null +++ b/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/Solution.cpp @@ -0,0 +1,30 @@ +class Solution { +public: + int countOfPairs(vector& nums) { + const int mod = 1e9 + 7; + int n = nums.size(); + int m = *max_element(nums.begin(), nums.end()); + vector> f(n, vector(m + 1)); + for (int j = 0; j <= nums[0]; ++j) { + f[0][j] = 1; + } + vector g(m + 1); + for (int i = 1; i < n; ++i) { + g[0] = f[i - 1][0]; + for (int j = 1; j <= m; ++j) { + g[j] = (g[j - 1] + f[i - 1][j]) % mod; + } + for (int j = 0; j <= nums[i]; ++j) { + int k = min(j, j + nums[i - 1] - nums[i]); + if (k >= 0) { + f[i][j] = g[k]; + } + } + } + int ans = 0; + for (int j = 0; j <= nums[n - 1]; ++j) { + ans = (ans + f[n - 1][j]) % mod; + } + return ans; + } +}; diff --git a/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/Solution.go b/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/Solution.go new file mode 100644 index 0000000000000..72ed9c30e80f3 --- /dev/null +++ b/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/Solution.go @@ -0,0 +1,29 @@ +func countOfPairs(nums []int) (ans int) { + const mod int = 1e9 + 7 + n := len(nums) + m := slices.Max(nums) + f := make([][]int, n) + for i := range f { + f[i] = make([]int, m+1) + } + for j := 0; j <= nums[0]; j++ { + f[0][j] = 1 + } + g := make([]int, m+1) + for i := 1; i < n; i++ { + g[0] = f[i-1][0] + for j := 1; j <= m; j++ { + g[j] = (g[j-1] + f[i-1][j]) % mod + } + for j := 0; j <= nums[i]; j++ { + k := min(j, j+nums[i-1]-nums[i]) + if k >= 0 { + f[i][j] = g[k] + } + } + } + for j := 0; j <= nums[n-1]; j++ { + ans = (ans + f[n-1][j]) % mod + } + return +} diff --git a/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/Solution.java b/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/Solution.java new file mode 100644 index 0000000000000..6391ae1136ff4 --- /dev/null +++ b/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/Solution.java @@ -0,0 +1,29 @@ +class Solution { + public int countOfPairs(int[] nums) { + final int mod = (int) 1e9 + 7; + int n = nums.length; + int m = Arrays.stream(nums).max().getAsInt(); + int[][] f = new int[n][m + 1]; + for (int j = 0; j <= nums[0]; ++j) { + f[0][j] = 1; + } + int[] g = new int[m + 1]; + for (int i = 1; i < n; ++i) { + g[0] = f[i - 1][0]; + for (int j = 1; j <= m; ++j) { + g[j] = (g[j - 1] + f[i - 1][j]) % mod; + } + for (int j = 0; j <= nums[i]; ++j) { + int k = Math.min(j, j + nums[i - 1] - nums[i]); + if (k >= 0) { + f[i][j] = g[k]; + } + } + } + int ans = 0; + for (int j = 0; j <= nums[n - 1]; ++j) { + ans = (ans + f[n - 1][j]) % mod; + } + return ans; + } +} diff --git a/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/Solution.py b/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/Solution.py new file mode 100644 index 0000000000000..cf4957154bf61 --- /dev/null +++ b/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/Solution.py @@ -0,0 +1,14 @@ +class Solution: + def countOfPairs(self, nums: List[int]) -> int: + mod = 10**9 + 7 + n, m = len(nums), max(nums) + f = [[0] * (m + 1) for _ in range(n)] + for j in range(nums[0] + 1): + f[0][j] = 1 + for i in range(1, n): + s = list(accumulate(f[i - 1])) + for j in range(nums[i] + 1): + k = min(j, j + nums[i - 1] - nums[i]) + if k >= 0: + f[i][j] = s[k] % mod + return sum(f[-1][: nums[-1] + 1]) % mod diff --git a/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/Solution.ts b/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/Solution.ts new file mode 100644 index 0000000000000..94b14790bc2e3 --- /dev/null +++ b/solution/3200-3299/3251.Find the Count of Monotonic Pairs II/Solution.ts @@ -0,0 +1,27 @@ +function countOfPairs(nums: number[]): number { + const mod = 1e9 + 7; + const n = nums.length; + const m = Math.max(...nums); + const f: number[][] = Array.from({ length: n }, () => Array(m + 1).fill(0)); + for (let j = 0; j <= nums[0]; j++) { + f[0][j] = 1; + } + const g: number[] = Array(m + 1).fill(0); + for (let i = 1; i < n; i++) { + g[0] = f[i - 1][0]; + for (let j = 1; j <= m; j++) { + g[j] = (g[j - 1] + f[i - 1][j]) % mod; + } + for (let j = 0; j <= nums[i]; j++) { + const k = Math.min(j, j + nums[i - 1] - nums[i]); + if (k >= 0) { + f[i][j] = g[k]; + } + } + } + let ans = 0; + for (let j = 0; j <= nums[n - 1]; j++) { + ans = (ans + f[n - 1][j]) % mod; + } + return ans; +} diff --git a/solution/CONTEST_README.md b/solution/CONTEST_README.md index 9e92b37c841b9..cae1c353ad573 100644 --- a/solution/CONTEST_README.md +++ b/solution/CONTEST_README.md @@ -26,6 +26,13 @@ comments: true ## 往期竞赛 +#### 第 410 场周赛(2024-08-11 10:30, 90 分钟) 参赛人数 2987 + +- [3248. 矩阵中的蛇](/solution/3200-3299/3248.Snake%20in%20Matrix/README.md) +- [3249. 统计好节点的数目](/solution/3200-3299/3249.Count%20the%20Number%20of%20Good%20Nodes/README.md) +- [3250. 单调数组对的数目 I](/solution/3200-3299/3250.Find%20the%20Count%20of%20Monotonic%20Pairs%20I/README.md) +- [3251. 单调数组对的数目 II](/solution/3200-3299/3251.Find%20the%20Count%20of%20Monotonic%20Pairs%20II/README.md) + #### 第 409 场周赛(2024-08-04 10:30, 90 分钟) 参赛人数 3643 - [3242. 设计相邻元素求和服务](/solution/3200-3299/3242.Design%20Neighbor%20Sum%20Service/README.md) diff --git a/solution/CONTEST_README_EN.md b/solution/CONTEST_README_EN.md index ed54924b06e68..0524eb350dfaa 100644 --- a/solution/CONTEST_README_EN.md +++ b/solution/CONTEST_README_EN.md @@ -29,6 +29,13 @@ If you want to estimate your score changes after the contest ends, you can visit ## Past Contests +#### Weekly Contest 410 + +- [3248. Snake in Matrix](/solution/3200-3299/3248.Snake%20in%20Matrix/README_EN.md) +- [3249. Count the Number of Good Nodes](/solution/3200-3299/3249.Count%20the%20Number%20of%20Good%20Nodes/README_EN.md) +- [3250. Find the Count of Monotonic Pairs I](/solution/3200-3299/3250.Find%20the%20Count%20of%20Monotonic%20Pairs%20I/README_EN.md) +- [3251. Find the Count of Monotonic Pairs II](/solution/3200-3299/3251.Find%20the%20Count%20of%20Monotonic%20Pairs%20II/README_EN.md) + #### Weekly Contest 409 - [3242. Design Neighbor Sum Service](/solution/3200-3299/3242.Design%20Neighbor%20Sum%20Service/README_EN.md) diff --git a/solution/README.md b/solution/README.md index cab5ed7dd8927..f49ad4f6d5d19 100644 --- a/solution/README.md +++ b/solution/README.md @@ -3258,6 +3258,10 @@ | 3245 | [交替组 III](/solution/3200-3299/3245.Alternating%20Groups%20III/README.md) | `树状数组`,`数组` | 困难 | 第 409 场周赛 | | 3246 | [英超积分榜排名](/solution/3200-3299/3246.Premier%20League%20Table%20Ranking/README.md) | `数据库` | 简单 | 🔒 | | 3247 | [奇数和子序列的数量](/solution/3200-3299/3247.Number%20of%20Subsequences%20with%20Odd%20Sum/README.md) | | 中等 | 🔒 | +| 3248 | [矩阵中的蛇](/solution/3200-3299/3248.Snake%20in%20Matrix/README.md) | | 简单 | 第 410 场周赛 | +| 3249 | [统计好节点的数目](/solution/3200-3299/3249.Count%20the%20Number%20of%20Good%20Nodes/README.md) | | 中等 | 第 410 场周赛 | +| 3250 | [单调数组对的数目 I](/solution/3200-3299/3250.Find%20the%20Count%20of%20Monotonic%20Pairs%20I/README.md) | | 困难 | 第 410 场周赛 | +| 3251 | [单调数组对的数目 II](/solution/3200-3299/3251.Find%20the%20Count%20of%20Monotonic%20Pairs%20II/README.md) | | 困难 | 第 410 场周赛 | ## 版权 diff --git a/solution/README_EN.md b/solution/README_EN.md index a14e9fb996174..20298ce0e86e7 100644 --- a/solution/README_EN.md +++ b/solution/README_EN.md @@ -3256,6 +3256,10 @@ Press Control + F(or Command + F on | 3245 | [Alternating Groups III](/solution/3200-3299/3245.Alternating%20Groups%20III/README_EN.md) | `Binary Indexed Tree`,`Array` | Hard | Weekly Contest 409 | | 3246 | [Premier League Table Ranking](/solution/3200-3299/3246.Premier%20League%20Table%20Ranking/README_EN.md) | `Database` | Easy | 🔒 | | 3247 | [Number of Subsequences with Odd Sum](/solution/3200-3299/3247.Number%20of%20Subsequences%20with%20Odd%20Sum/README_EN.md) | | Medium | 🔒 | +| 3248 | [Snake in Matrix](/solution/3200-3299/3248.Snake%20in%20Matrix/README_EN.md) | | Easy | Weekly Contest 410 | +| 3249 | [Count the Number of Good Nodes](/solution/3200-3299/3249.Count%20the%20Number%20of%20Good%20Nodes/README_EN.md) | | Medium | Weekly Contest 410 | +| 3250 | [Find the Count of Monotonic Pairs I](/solution/3200-3299/3250.Find%20the%20Count%20of%20Monotonic%20Pairs%20I/README_EN.md) | | Hard | Weekly Contest 410 | +| 3251 | [Find the Count of Monotonic Pairs II](/solution/3200-3299/3251.Find%20the%20Count%20of%20Monotonic%20Pairs%20II/README_EN.md) | | Hard | Weekly Contest 410 | ## Copyright diff --git a/solution/contest.json b/solution/contest.json index 855229c2b1370..604f6663ab846 100644 --- a/solution/contest.json +++ b/solution/contest.json @@ -1 +1 @@ -[{"contest_title": "\u7b2c 83 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 83", "contest_title_slug": "weekly-contest-83", "contest_id": 5, "contest_start_time": 1525570200, "contest_duration": 5400, "user_num": 58, "question_slugs": ["positions-of-large-groups", "masking-personal-information", "consecutive-numbers-sum", "count-unique-characters-of-all-substrings-of-a-given-string"]}, {"contest_title": "\u7b2c 84 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 84", "contest_title_slug": "weekly-contest-84", "contest_id": 6, "contest_start_time": 1526175000, "contest_duration": 5400, "user_num": 656, "question_slugs": ["flipping-an-image", "find-and-replace-in-string", "image-overlap", "sum-of-distances-in-tree"]}, {"contest_title": "\u7b2c 85 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 85", "contest_title_slug": "weekly-contest-85", "contest_id": 7, "contest_start_time": 1526779800, "contest_duration": 5400, "user_num": 467, "question_slugs": ["rectangle-overlap", "push-dominoes", "new-21-game", "similar-string-groups"]}, {"contest_title": "\u7b2c 86 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 86", "contest_title_slug": "weekly-contest-86", "contest_id": 8, "contest_start_time": 1527384600, "contest_duration": 5400, "user_num": 377, "question_slugs": ["magic-squares-in-grid", "keys-and-rooms", "split-array-into-fibonacci-sequence", "guess-the-word"]}, {"contest_title": "\u7b2c 87 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 87", "contest_title_slug": "weekly-contest-87", "contest_id": 9, "contest_start_time": 1527989400, "contest_duration": 5400, "user_num": 343, "question_slugs": ["backspace-string-compare", "longest-mountain-in-array", "hand-of-straights", "shortest-path-visiting-all-nodes"]}, {"contest_title": "\u7b2c 88 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 88", "contest_title_slug": "weekly-contest-88", "contest_id": 11, "contest_start_time": 1528594200, "contest_duration": 5400, "user_num": 404, "question_slugs": ["shifting-letters", "maximize-distance-to-closest-person", "loud-and-rich", "rectangle-area-ii"]}, {"contest_title": "\u7b2c 89 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 89", "contest_title_slug": "weekly-contest-89", "contest_id": 12, "contest_start_time": 1529199000, "contest_duration": 5400, "user_num": 491, "question_slugs": ["peak-index-in-a-mountain-array", "car-fleet", "exam-room", "k-similar-strings"]}, {"contest_title": "\u7b2c 90 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 90", "contest_title_slug": "weekly-contest-90", "contest_id": 13, "contest_start_time": 1529803800, "contest_duration": 5400, "user_num": 573, "question_slugs": ["buddy-strings", "score-of-parentheses", "mirror-reflection", "minimum-cost-to-hire-k-workers"]}, {"contest_title": "\u7b2c 91 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 91", "contest_title_slug": "weekly-contest-91", "contest_id": 14, "contest_start_time": 1530408600, "contest_duration": 5400, "user_num": 578, "question_slugs": ["lemonade-change", "all-nodes-distance-k-in-binary-tree", "score-after-flipping-matrix", "shortest-subarray-with-sum-at-least-k"]}, {"contest_title": "\u7b2c 92 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 92", "contest_title_slug": "weekly-contest-92", "contest_id": 15, "contest_start_time": 1531013400, "contest_duration": 5400, "user_num": 610, "question_slugs": ["transpose-matrix", "smallest-subtree-with-all-the-deepest-nodes", "prime-palindrome", "shortest-path-to-get-all-keys"]}, {"contest_title": "\u7b2c 93 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 93", "contest_title_slug": "weekly-contest-93", "contest_id": 16, "contest_start_time": 1531618200, "contest_duration": 5400, "user_num": 732, "question_slugs": ["binary-gap", "reordered-power-of-2", "advantage-shuffle", "minimum-number-of-refueling-stops"]}, {"contest_title": "\u7b2c 94 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 94", "contest_title_slug": "weekly-contest-94", "contest_id": 17, "contest_start_time": 1532223000, "contest_duration": 5400, "user_num": 733, "question_slugs": ["leaf-similar-trees", "walking-robot-simulation", "koko-eating-bananas", "length-of-longest-fibonacci-subsequence"]}, {"contest_title": "\u7b2c 95 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 95", "contest_title_slug": "weekly-contest-95", "contest_id": 18, "contest_start_time": 1532827800, "contest_duration": 5400, "user_num": 831, "question_slugs": ["middle-of-the-linked-list", "stone-game", "nth-magical-number", "profitable-schemes"]}, {"contest_title": "\u7b2c 96 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 96", "contest_title_slug": "weekly-contest-96", "contest_id": 19, "contest_start_time": 1533432600, "contest_duration": 5400, "user_num": 789, "question_slugs": ["projection-area-of-3d-shapes", "boats-to-save-people", "decoded-string-at-index", "reachable-nodes-in-subdivided-graph"]}, {"contest_title": "\u7b2c 97 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 97", "contest_title_slug": "weekly-contest-97", "contest_id": 20, "contest_start_time": 1534037400, "contest_duration": 5400, "user_num": 635, "question_slugs": ["uncommon-words-from-two-sentences", "spiral-matrix-iii", "possible-bipartition", "super-egg-drop"]}, {"contest_title": "\u7b2c 98 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 98", "contest_title_slug": "weekly-contest-98", "contest_id": 21, "contest_start_time": 1534642200, "contest_duration": 5400, "user_num": 670, "question_slugs": ["fair-candy-swap", "find-and-replace-pattern", "construct-binary-tree-from-preorder-and-postorder-traversal", "sum-of-subsequence-widths"]}, {"contest_title": "\u7b2c 99 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 99", "contest_title_slug": "weekly-contest-99", "contest_id": 22, "contest_start_time": 1535247000, "contest_duration": 5400, "user_num": 725, "question_slugs": ["surface-area-of-3d-shapes", "groups-of-special-equivalent-strings", "all-possible-full-binary-trees", "maximum-frequency-stack"]}, {"contest_title": "\u7b2c 100 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 100", "contest_title_slug": "weekly-contest-100", "contest_id": 23, "contest_start_time": 1535851800, "contest_duration": 5400, "user_num": 718, "question_slugs": ["monotonic-array", "increasing-order-search-tree", "bitwise-ors-of-subarrays", "orderly-queue"]}, {"contest_title": "\u7b2c 101 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 101", "contest_title_slug": "weekly-contest-101", "contest_id": 24, "contest_start_time": 1536456600, "contest_duration": 6300, "user_num": 854, "question_slugs": ["rle-iterator", "online-stock-span", "numbers-at-most-n-given-digit-set", "valid-permutations-for-di-sequence"]}, {"contest_title": "\u7b2c 102 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 102", "contest_title_slug": "weekly-contest-102", "contest_id": 25, "contest_start_time": 1537061400, "contest_duration": 5400, "user_num": 660, "question_slugs": ["sort-array-by-parity", "fruit-into-baskets", "sum-of-subarray-minimums", "super-palindromes"]}, {"contest_title": "\u7b2c 103 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 103", "contest_title_slug": "weekly-contest-103", "contest_id": 26, "contest_start_time": 1537666200, "contest_duration": 5400, "user_num": 575, "question_slugs": ["smallest-range-i", "snakes-and-ladders", "smallest-range-ii", "online-election"]}, {"contest_title": "\u7b2c 104 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 104", "contest_title_slug": "weekly-contest-104", "contest_id": 27, "contest_start_time": 1538271000, "contest_duration": 5400, "user_num": 354, "question_slugs": ["x-of-a-kind-in-a-deck-of-cards", "partition-array-into-disjoint-intervals", "word-subsets", "cat-and-mouse"]}, {"contest_title": "\u7b2c 105 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 105", "contest_title_slug": "weekly-contest-105", "contest_id": 28, "contest_start_time": 1538875800, "contest_duration": 5400, "user_num": 393, "question_slugs": ["reverse-only-letters", "maximum-sum-circular-subarray", "complete-binary-tree-inserter", "number-of-music-playlists"]}, {"contest_title": "\u7b2c 106 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 106", "contest_title_slug": "weekly-contest-106", "contest_id": 29, "contest_start_time": 1539480600, "contest_duration": 5400, "user_num": 369, "question_slugs": ["sort-array-by-parity-ii", "minimum-add-to-make-parentheses-valid", "3sum-with-multiplicity", "minimize-malware-spread"]}, {"contest_title": "\u7b2c 107 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 107", "contest_title_slug": "weekly-contest-107", "contest_id": 30, "contest_start_time": 1540085400, "contest_duration": 5400, "user_num": 504, "question_slugs": ["long-pressed-name", "flip-string-to-monotone-increasing", "three-equal-parts", "minimize-malware-spread-ii"]}, {"contest_title": "\u7b2c 108 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 108", "contest_title_slug": "weekly-contest-108", "contest_id": 31, "contest_start_time": 1540690200, "contest_duration": 5400, "user_num": 524, "question_slugs": ["unique-email-addresses", "binary-subarrays-with-sum", "minimum-falling-path-sum", "beautiful-array"]}, {"contest_title": "\u7b2c 109 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 109", "contest_title_slug": "weekly-contest-109", "contest_id": 32, "contest_start_time": 1541295000, "contest_duration": 5400, "user_num": 439, "question_slugs": ["number-of-recent-calls", "knight-dialer", "shortest-bridge", "stamping-the-sequence"]}, {"contest_title": "\u7b2c 110 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 110", "contest_title_slug": "weekly-contest-110", "contest_id": 33, "contest_start_time": 1541903400, "contest_duration": 5400, "user_num": 346, "question_slugs": ["reorder-data-in-log-files", "range-sum-of-bst", "minimum-area-rectangle", "distinct-subsequences-ii"]}, {"contest_title": "\u7b2c 111 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 111", "contest_title_slug": "weekly-contest-111", "contest_id": 34, "contest_start_time": 1542508200, "contest_duration": 5400, "user_num": 353, "question_slugs": ["valid-mountain-array", "delete-columns-to-make-sorted", "di-string-match", "find-the-shortest-superstring"]}, {"contest_title": "\u7b2c 112 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 112", "contest_title_slug": "weekly-contest-112", "contest_id": 35, "contest_start_time": 1543113000, "contest_duration": 5400, "user_num": 299, "question_slugs": ["minimum-increment-to-make-array-unique", "validate-stack-sequences", "most-stones-removed-with-same-row-or-column", "bag-of-tokens"]}, {"contest_title": "\u7b2c 113 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 113", "contest_title_slug": "weekly-contest-113", "contest_id": 36, "contest_start_time": 1543717800, "contest_duration": 5400, "user_num": 462, "question_slugs": ["largest-time-for-given-digits", "flip-equivalent-binary-trees", "reveal-cards-in-increasing-order", "largest-component-size-by-common-factor"]}, {"contest_title": "\u7b2c 114 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 114", "contest_title_slug": "weekly-contest-114", "contest_id": 37, "contest_start_time": 1544322600, "contest_duration": 5400, "user_num": 391, "question_slugs": ["verifying-an-alien-dictionary", "array-of-doubled-pairs", "delete-columns-to-make-sorted-ii", "tallest-billboard"]}, {"contest_title": "\u7b2c 115 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 115", "contest_title_slug": "weekly-contest-115", "contest_id": 38, "contest_start_time": 1544927400, "contest_duration": 5400, "user_num": 383, "question_slugs": ["prison-cells-after-n-days", "check-completeness-of-a-binary-tree", "regions-cut-by-slashes", "delete-columns-to-make-sorted-iii"]}, {"contest_title": "\u7b2c 116 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 116", "contest_title_slug": "weekly-contest-116", "contest_id": 39, "contest_start_time": 1545532200, "contest_duration": 5400, "user_num": 369, "question_slugs": ["n-repeated-element-in-size-2n-array", "maximum-width-ramp", "minimum-area-rectangle-ii", "least-operators-to-express-number"]}, {"contest_title": "\u7b2c 117 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 117", "contest_title_slug": "weekly-contest-117", "contest_id": 41, "contest_start_time": 1546137000, "contest_duration": 5400, "user_num": 657, "question_slugs": ["univalued-binary-tree", "numbers-with-same-consecutive-differences", "vowel-spellchecker", "binary-tree-cameras"]}, {"contest_title": "\u7b2c 118 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 118", "contest_title_slug": "weekly-contest-118", "contest_id": 42, "contest_start_time": 1546741800, "contest_duration": 5400, "user_num": 383, "question_slugs": ["powerful-integers", "pancake-sorting", "flip-binary-tree-to-match-preorder-traversal", "equal-rational-numbers"]}, {"contest_title": "\u7b2c 119 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 119", "contest_title_slug": "weekly-contest-119", "contest_id": 43, "contest_start_time": 1547346600, "contest_duration": 5400, "user_num": 513, "question_slugs": ["k-closest-points-to-origin", "largest-perimeter-triangle", "subarray-sums-divisible-by-k", "odd-even-jump"]}, {"contest_title": "\u7b2c 120 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 120", "contest_title_slug": "weekly-contest-120", "contest_id": 44, "contest_start_time": 1547951400, "contest_duration": 5400, "user_num": 382, "question_slugs": ["squares-of-a-sorted-array", "longest-turbulent-subarray", "distribute-coins-in-binary-tree", "unique-paths-iii"]}, {"contest_title": "\u7b2c 121 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 121", "contest_title_slug": "weekly-contest-121", "contest_id": 45, "contest_start_time": 1548556200, "contest_duration": 5400, "user_num": 384, "question_slugs": ["string-without-aaa-or-bbb", "time-based-key-value-store", "minimum-cost-for-tickets", "triples-with-bitwise-and-equal-to-zero"]}, {"contest_title": "\u7b2c 122 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 122", "contest_title_slug": "weekly-contest-122", "contest_id": 46, "contest_start_time": 1549161000, "contest_duration": 5400, "user_num": 280, "question_slugs": ["sum-of-even-numbers-after-queries", "smallest-string-starting-from-leaf", "interval-list-intersections", "vertical-order-traversal-of-a-binary-tree"]}, {"contest_title": "\u7b2c 123 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 123", "contest_title_slug": "weekly-contest-123", "contest_id": 47, "contest_start_time": 1549765800, "contest_duration": 5400, "user_num": 247, "question_slugs": ["add-to-array-form-of-integer", "satisfiability-of-equality-equations", "broken-calculator", "subarrays-with-k-different-integers"]}, {"contest_title": "\u7b2c 124 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 124", "contest_title_slug": "weekly-contest-124", "contest_id": 48, "contest_start_time": 1550370600, "contest_duration": 5400, "user_num": 417, "question_slugs": ["cousins-in-binary-tree", "rotting-oranges", "minimum-number-of-k-consecutive-bit-flips", "number-of-squareful-arrays"]}, {"contest_title": "\u7b2c 125 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 125", "contest_title_slug": "weekly-contest-125", "contest_id": 49, "contest_start_time": 1550975400, "contest_duration": 5400, "user_num": 469, "question_slugs": ["find-the-town-judge", "available-captures-for-rook", "maximum-binary-tree-ii", "grid-illumination"]}, {"contest_title": "\u7b2c 126 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 126", "contest_title_slug": "weekly-contest-126", "contest_id": 50, "contest_start_time": 1551580200, "contest_duration": 5400, "user_num": 591, "question_slugs": ["find-common-characters", "check-if-word-is-valid-after-substitutions", "max-consecutive-ones-iii", "minimum-cost-to-merge-stones"]}, {"contest_title": "\u7b2c 127 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 127", "contest_title_slug": "weekly-contest-127", "contest_id": 52, "contest_start_time": 1552185000, "contest_duration": 5400, "user_num": 664, "question_slugs": ["maximize-sum-of-array-after-k-negations", "clumsy-factorial", "minimum-domino-rotations-for-equal-row", "construct-binary-search-tree-from-preorder-traversal"]}, {"contest_title": "\u7b2c 128 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 128", "contest_title_slug": "weekly-contest-128", "contest_id": 53, "contest_start_time": 1552789800, "contest_duration": 5400, "user_num": 1251, "question_slugs": ["complement-of-base-10-integer", "pairs-of-songs-with-total-durations-divisible-by-60", "capacity-to-ship-packages-within-d-days", "numbers-with-repeated-digits"]}, {"contest_title": "\u7b2c 129 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 129", "contest_title_slug": "weekly-contest-129", "contest_id": 54, "contest_start_time": 1553391000, "contest_duration": 5400, "user_num": 759, "question_slugs": ["partition-array-into-three-parts-with-equal-sum", "smallest-integer-divisible-by-k", "best-sightseeing-pair", "binary-string-with-substrings-representing-1-to-n"]}, {"contest_title": "\u7b2c 130 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 130", "contest_title_slug": "weekly-contest-130", "contest_id": 55, "contest_start_time": 1553999400, "contest_duration": 5400, "user_num": 1294, "question_slugs": ["binary-prefix-divisible-by-5", "convert-to-base-2", "next-greater-node-in-linked-list", "number-of-enclaves"]}, {"contest_title": "\u7b2c 131 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 131", "contest_title_slug": "weekly-contest-131", "contest_id": 56, "contest_start_time": 1554604200, "contest_duration": 5400, "user_num": 918, "question_slugs": ["remove-outermost-parentheses", "sum-of-root-to-leaf-binary-numbers", "camelcase-matching", "video-stitching"]}, {"contest_title": "\u7b2c 132 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 132", "contest_title_slug": "weekly-contest-132", "contest_id": 57, "contest_start_time": 1555209000, "contest_duration": 5400, "user_num": 1050, "question_slugs": ["divisor-game", "maximum-difference-between-node-and-ancestor", "longest-arithmetic-subsequence", "recover-a-tree-from-preorder-traversal"]}, {"contest_title": "\u7b2c 133 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 133", "contest_title_slug": "weekly-contest-133", "contest_id": 59, "contest_start_time": 1555813800, "contest_duration": 5400, "user_num": 999, "question_slugs": ["two-city-scheduling", "matrix-cells-in-distance-order", "maximum-sum-of-two-non-overlapping-subarrays", "stream-of-characters"]}, {"contest_title": "\u7b2c 134 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 134", "contest_title_slug": "weekly-contest-134", "contest_id": 64, "contest_start_time": 1556418600, "contest_duration": 5400, "user_num": 728, "question_slugs": ["moving-stones-until-consecutive", "coloring-a-border", "uncrossed-lines", "escape-a-large-maze"]}, {"contest_title": "\u7b2c 135 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 135", "contest_title_slug": "weekly-contest-135", "contest_id": 65, "contest_start_time": 1557023400, "contest_duration": 5400, "user_num": 549, "question_slugs": ["valid-boomerang", "binary-search-tree-to-greater-sum-tree", "minimum-score-triangulation-of-polygon", "moving-stones-until-consecutive-ii"]}, {"contest_title": "\u7b2c 136 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 136", "contest_title_slug": "weekly-contest-136", "contest_id": 66, "contest_start_time": 1557628200, "contest_duration": 5400, "user_num": 790, "question_slugs": ["robot-bounded-in-circle", "flower-planting-with-no-adjacent", "partition-array-for-maximum-sum", "longest-duplicate-substring"]}, {"contest_title": "\u7b2c 137 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 137", "contest_title_slug": "weekly-contest-137", "contest_id": 67, "contest_start_time": 1558233000, "contest_duration": 5400, "user_num": 766, "question_slugs": ["last-stone-weight", "remove-all-adjacent-duplicates-in-string", "longest-string-chain", "last-stone-weight-ii"]}, {"contest_title": "\u7b2c 138 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 138", "contest_title_slug": "weekly-contest-138", "contest_id": 68, "contest_start_time": 1558837800, "contest_duration": 5400, "user_num": 752, "question_slugs": ["height-checker", "grumpy-bookstore-owner", "previous-permutation-with-one-swap", "distant-barcodes"]}, {"contest_title": "\u7b2c 139 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 139", "contest_title_slug": "weekly-contest-139", "contest_id": 69, "contest_start_time": 1559442600, "contest_duration": 5400, "user_num": 785, "question_slugs": ["greatest-common-divisor-of-strings", "flip-columns-for-maximum-number-of-equal-rows", "adding-two-negabinary-numbers", "number-of-submatrices-that-sum-to-target"]}, {"contest_title": "\u7b2c 140 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 140", "contest_title_slug": "weekly-contest-140", "contest_id": 71, "contest_start_time": 1560047400, "contest_duration": 5400, "user_num": 660, "question_slugs": ["occurrences-after-bigram", "letter-tile-possibilities", "insufficient-nodes-in-root-to-leaf-paths", "smallest-subsequence-of-distinct-characters"]}, {"contest_title": "\u7b2c 141 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 141", "contest_title_slug": "weekly-contest-141", "contest_id": 72, "contest_start_time": 1560652200, "contest_duration": 5400, "user_num": 763, "question_slugs": ["duplicate-zeros", "largest-values-from-labels", "shortest-path-in-binary-matrix", "shortest-common-supersequence"]}, {"contest_title": "\u7b2c 142 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 142", "contest_title_slug": "weekly-contest-142", "contest_id": 74, "contest_start_time": 1561257000, "contest_duration": 5400, "user_num": 801, "question_slugs": ["statistics-from-a-large-sample", "car-pooling", "find-in-mountain-array", "brace-expansion-ii"]}, {"contest_title": "\u7b2c 143 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 143", "contest_title_slug": "weekly-contest-143", "contest_id": 84, "contest_start_time": 1561861800, "contest_duration": 5400, "user_num": 803, "question_slugs": ["distribute-candies-to-people", "path-in-zigzag-labelled-binary-tree", "filling-bookcase-shelves", "parsing-a-boolean-expression"]}, {"contest_title": "\u7b2c 144 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 144", "contest_title_slug": "weekly-contest-144", "contest_id": 86, "contest_start_time": 1562466600, "contest_duration": 5400, "user_num": 777, "question_slugs": ["defanging-an-ip-address", "corporate-flight-bookings", "delete-nodes-and-return-forest", "maximum-nesting-depth-of-two-valid-parentheses-strings"]}, {"contest_title": "\u7b2c 145 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 145", "contest_title_slug": "weekly-contest-145", "contest_id": 87, "contest_start_time": 1563071400, "contest_duration": 5400, "user_num": 1114, "question_slugs": ["relative-sort-array", "lowest-common-ancestor-of-deepest-leaves", "longest-well-performing-interval", "smallest-sufficient-team"]}, {"contest_title": "\u7b2c 146 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 146", "contest_title_slug": "weekly-contest-146", "contest_id": 89, "contest_start_time": 1563676200, "contest_duration": 5400, "user_num": 1189, "question_slugs": ["number-of-equivalent-domino-pairs", "shortest-path-with-alternating-colors", "minimum-cost-tree-from-leaf-values", "maximum-of-absolute-value-expression"]}, {"contest_title": "\u7b2c 147 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 147", "contest_title_slug": "weekly-contest-147", "contest_id": 90, "contest_start_time": 1564281000, "contest_duration": 5400, "user_num": 1132, "question_slugs": ["n-th-tribonacci-number", "alphabet-board-path", "largest-1-bordered-square", "stone-game-ii"]}, {"contest_title": "\u7b2c 148 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 148", "contest_title_slug": "weekly-contest-148", "contest_id": 93, "contest_start_time": 1564885800, "contest_duration": 5400, "user_num": 1251, "question_slugs": ["decrease-elements-to-make-array-zigzag", "binary-tree-coloring-game", "snapshot-array", "longest-chunked-palindrome-decomposition"]}, {"contest_title": "\u7b2c 149 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 149", "contest_title_slug": "weekly-contest-149", "contest_id": 94, "contest_start_time": 1565490600, "contest_duration": 5400, "user_num": 1351, "question_slugs": ["day-of-the-year", "number-of-dice-rolls-with-target-sum", "swap-for-longest-repeated-character-substring", "online-majority-element-in-subarray"]}, {"contest_title": "\u7b2c 150 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 150", "contest_title_slug": "weekly-contest-150", "contest_id": 96, "contest_start_time": 1566095400, "contest_duration": 5400, "user_num": 1473, "question_slugs": ["find-words-that-can-be-formed-by-characters", "maximum-level-sum-of-a-binary-tree", "as-far-from-land-as-possible", "last-substring-in-lexicographical-order"]}, {"contest_title": "\u7b2c 151 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 151", "contest_title_slug": "weekly-contest-151", "contest_id": 98, "contest_start_time": 1566700200, "contest_duration": 5400, "user_num": 1341, "question_slugs": ["invalid-transactions", "compare-strings-by-frequency-of-the-smallest-character", "remove-zero-sum-consecutive-nodes-from-linked-list", "dinner-plate-stacks"]}, {"contest_title": "\u7b2c 152 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 152", "contest_title_slug": "weekly-contest-152", "contest_id": 100, "contest_start_time": 1567305000, "contest_duration": 5400, "user_num": 1367, "question_slugs": ["prime-arrangements", "diet-plan-performance", "can-make-palindrome-from-substring", "number-of-valid-words-for-each-puzzle"]}, {"contest_title": "\u7b2c 153 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 153", "contest_title_slug": "weekly-contest-153", "contest_id": 102, "contest_start_time": 1567909800, "contest_duration": 5400, "user_num": 1434, "question_slugs": ["distance-between-bus-stops", "day-of-the-week", "maximum-subarray-sum-with-one-deletion", "make-array-strictly-increasing"]}, {"contest_title": "\u7b2c 154 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 154", "contest_title_slug": "weekly-contest-154", "contest_id": 106, "contest_start_time": 1568514600, "contest_duration": 5400, "user_num": 1299, "question_slugs": ["maximum-number-of-balloons", "reverse-substrings-between-each-pair-of-parentheses", "k-concatenation-maximum-sum", "critical-connections-in-a-network"]}, {"contest_title": "\u7b2c 155 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 155", "contest_title_slug": "weekly-contest-155", "contest_id": 107, "contest_start_time": 1569119400, "contest_duration": 5400, "user_num": 1603, "question_slugs": ["minimum-absolute-difference", "ugly-number-iii", "smallest-string-with-swaps", "sort-items-by-groups-respecting-dependencies"]}, {"contest_title": "\u7b2c 156 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 156", "contest_title_slug": "weekly-contest-156", "contest_id": 113, "contest_start_time": 1569724200, "contest_duration": 5400, "user_num": 1433, "question_slugs": ["unique-number-of-occurrences", "get-equal-substrings-within-budget", "remove-all-adjacent-duplicates-in-string-ii", "minimum-moves-to-reach-target-with-rotations"]}, {"contest_title": "\u7b2c 157 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 157", "contest_title_slug": "weekly-contest-157", "contest_id": 114, "contest_start_time": 1570329000, "contest_duration": 5400, "user_num": 1217, "question_slugs": ["minimum-cost-to-move-chips-to-the-same-position", "longest-arithmetic-subsequence-of-given-difference", "path-with-maximum-gold", "count-vowels-permutation"]}, {"contest_title": "\u7b2c 158 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 158", "contest_title_slug": "weekly-contest-158", "contest_id": 116, "contest_start_time": 1570933800, "contest_duration": 5400, "user_num": 1716, "question_slugs": ["split-a-string-in-balanced-strings", "queens-that-can-attack-the-king", "dice-roll-simulation", "maximum-equal-frequency"]}, {"contest_title": "\u7b2c 159 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 159", "contest_title_slug": "weekly-contest-159", "contest_id": 117, "contest_start_time": 1571538600, "contest_duration": 5400, "user_num": 1634, "question_slugs": ["check-if-it-is-a-straight-line", "remove-sub-folders-from-the-filesystem", "replace-the-substring-for-balanced-string", "maximum-profit-in-job-scheduling"]}, {"contest_title": "\u7b2c 160 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 160", "contest_title_slug": "weekly-contest-160", "contest_id": 119, "contest_start_time": 1572143400, "contest_duration": 5400, "user_num": 1692, "question_slugs": ["find-positive-integer-solution-for-a-given-equation", "circular-permutation-in-binary-representation", "maximum-length-of-a-concatenated-string-with-unique-characters", "tiling-a-rectangle-with-the-fewest-squares"]}, {"contest_title": "\u7b2c 161 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 161", "contest_title_slug": "weekly-contest-161", "contest_id": 120, "contest_start_time": 1572748200, "contest_duration": 5400, "user_num": 1610, "question_slugs": ["minimum-swaps-to-make-strings-equal", "count-number-of-nice-subarrays", "minimum-remove-to-make-valid-parentheses", "check-if-it-is-a-good-array"]}, {"contest_title": "\u7b2c 162 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 162", "contest_title_slug": "weekly-contest-162", "contest_id": 122, "contest_start_time": 1573353000, "contest_duration": 5400, "user_num": 1569, "question_slugs": ["cells-with-odd-values-in-a-matrix", "reconstruct-a-2-row-binary-matrix", "number-of-closed-islands", "maximum-score-words-formed-by-letters"]}, {"contest_title": "\u7b2c 163 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 163", "contest_title_slug": "weekly-contest-163", "contest_id": 123, "contest_start_time": 1573957800, "contest_duration": 5400, "user_num": 1605, "question_slugs": ["shift-2d-grid", "find-elements-in-a-contaminated-binary-tree", "greatest-sum-divisible-by-three", "minimum-moves-to-move-a-box-to-their-target-location"]}, {"contest_title": "\u7b2c 164 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 164", "contest_title_slug": "weekly-contest-164", "contest_id": 125, "contest_start_time": 1574562600, "contest_duration": 5400, "user_num": 1676, "question_slugs": ["minimum-time-visiting-all-points", "count-servers-that-communicate", "search-suggestions-system", "number-of-ways-to-stay-in-the-same-place-after-some-steps"]}, {"contest_title": "\u7b2c 165 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 165", "contest_title_slug": "weekly-contest-165", "contest_id": 128, "contest_start_time": 1575167400, "contest_duration": 5400, "user_num": 1660, "question_slugs": ["find-winner-on-a-tic-tac-toe-game", "number-of-burgers-with-no-waste-of-ingredients", "count-square-submatrices-with-all-ones", "palindrome-partitioning-iii"]}, {"contest_title": "\u7b2c 166 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 166", "contest_title_slug": "weekly-contest-166", "contest_id": 130, "contest_start_time": 1575772200, "contest_duration": 5400, "user_num": 1676, "question_slugs": ["subtract-the-product-and-sum-of-digits-of-an-integer", "group-the-people-given-the-group-size-they-belong-to", "find-the-smallest-divisor-given-a-threshold", "minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix"]}, {"contest_title": "\u7b2c 167 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 167", "contest_title_slug": "weekly-contest-167", "contest_id": 131, "contest_start_time": 1576377000, "contest_duration": 5400, "user_num": 1537, "question_slugs": ["convert-binary-number-in-a-linked-list-to-integer", "sequential-digits", "maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold", "shortest-path-in-a-grid-with-obstacles-elimination"]}, {"contest_title": "\u7b2c 168 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 168", "contest_title_slug": "weekly-contest-168", "contest_id": 133, "contest_start_time": 1576981800, "contest_duration": 5400, "user_num": 1553, "question_slugs": ["find-numbers-with-even-number-of-digits", "divide-array-in-sets-of-k-consecutive-numbers", "maximum-number-of-occurrences-of-a-substring", "maximum-candies-you-can-get-from-boxes"]}, {"contest_title": "\u7b2c 169 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 169", "contest_title_slug": "weekly-contest-169", "contest_id": 134, "contest_start_time": 1577586600, "contest_duration": 5400, "user_num": 1568, "question_slugs": ["find-n-unique-integers-sum-up-to-zero", "all-elements-in-two-binary-search-trees", "jump-game-iii", "verbal-arithmetic-puzzle"]}, {"contest_title": "\u7b2c 170 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 170", "contest_title_slug": "weekly-contest-170", "contest_id": 136, "contest_start_time": 1578191400, "contest_duration": 5400, "user_num": 1649, "question_slugs": ["decrypt-string-from-alphabet-to-integer-mapping", "xor-queries-of-a-subarray", "get-watched-videos-by-your-friends", "minimum-insertion-steps-to-make-a-string-palindrome"]}, {"contest_title": "\u7b2c 171 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 171", "contest_title_slug": "weekly-contest-171", "contest_id": 137, "contest_start_time": 1578796200, "contest_duration": 5400, "user_num": 1708, "question_slugs": ["convert-integer-to-the-sum-of-two-no-zero-integers", "minimum-flips-to-make-a-or-b-equal-to-c", "number-of-operations-to-make-network-connected", "minimum-distance-to-type-a-word-using-two-fingers"]}, {"contest_title": "\u7b2c 172 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 172", "contest_title_slug": "weekly-contest-172", "contest_id": 139, "contest_start_time": 1579401000, "contest_duration": 5400, "user_num": 1415, "question_slugs": ["maximum-69-number", "print-words-vertically", "delete-leaves-with-a-given-value", "minimum-number-of-taps-to-open-to-water-a-garden"]}, {"contest_title": "\u7b2c 173 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 173", "contest_title_slug": "weekly-contest-173", "contest_id": 142, "contest_start_time": 1580005800, "contest_duration": 5400, "user_num": 1072, "question_slugs": ["remove-palindromic-subsequences", "filter-restaurants-by-vegan-friendly-price-and-distance", "find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance", "minimum-difficulty-of-a-job-schedule"]}, {"contest_title": "\u7b2c 174 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 174", "contest_title_slug": "weekly-contest-174", "contest_id": 144, "contest_start_time": 1580610600, "contest_duration": 5400, "user_num": 1660, "question_slugs": ["the-k-weakest-rows-in-a-matrix", "reduce-array-size-to-the-half", "maximum-product-of-splitted-binary-tree", "jump-game-v"]}, {"contest_title": "\u7b2c 175 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 175", "contest_title_slug": "weekly-contest-175", "contest_id": 145, "contest_start_time": 1581215400, "contest_duration": 5400, "user_num": 2048, "question_slugs": ["check-if-n-and-its-double-exist", "minimum-number-of-steps-to-make-two-strings-anagram", "tweet-counts-per-frequency", "maximum-students-taking-exam"]}, {"contest_title": "\u7b2c 176 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 176", "contest_title_slug": "weekly-contest-176", "contest_id": 147, "contest_start_time": 1581820200, "contest_duration": 5400, "user_num": 2410, "question_slugs": ["count-negative-numbers-in-a-sorted-matrix", "product-of-the-last-k-numbers", "maximum-number-of-events-that-can-be-attended", "construct-target-array-with-multiple-sums"]}, {"contest_title": "\u7b2c 177 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 177", "contest_title_slug": "weekly-contest-177", "contest_id": 148, "contest_start_time": 1582425000, "contest_duration": 5400, "user_num": 2986, "question_slugs": ["number-of-days-between-two-dates", "validate-binary-tree-nodes", "closest-divisors", "largest-multiple-of-three"]}, {"contest_title": "\u7b2c 178 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 178", "contest_title_slug": "weekly-contest-178", "contest_id": 154, "contest_start_time": 1583029800, "contest_duration": 5400, "user_num": 3305, "question_slugs": ["how-many-numbers-are-smaller-than-the-current-number", "rank-teams-by-votes", "linked-list-in-binary-tree", "minimum-cost-to-make-at-least-one-valid-path-in-a-grid"]}, {"contest_title": "\u7b2c 179 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 179", "contest_title_slug": "weekly-contest-179", "contest_id": 156, "contest_start_time": 1583634600, "contest_duration": 5400, "user_num": 3606, "question_slugs": ["generate-a-string-with-characters-that-have-odd-counts", "number-of-times-binary-string-is-prefix-aligned", "time-needed-to-inform-all-employees", "frog-position-after-t-seconds"]}, {"contest_title": "\u7b2c 180 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 180", "contest_title_slug": "weekly-contest-180", "contest_id": 160, "contest_start_time": 1584239400, "contest_duration": 5400, "user_num": 3715, "question_slugs": ["lucky-numbers-in-a-matrix", "design-a-stack-with-increment-operation", "balance-a-binary-search-tree", "maximum-performance-of-a-team"]}, {"contest_title": "\u7b2c 181 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 181", "contest_title_slug": "weekly-contest-181", "contest_id": 162, "contest_start_time": 1584844200, "contest_duration": 5400, "user_num": 4149, "question_slugs": ["create-target-array-in-the-given-order", "four-divisors", "check-if-there-is-a-valid-path-in-a-grid", "longest-happy-prefix"]}, {"contest_title": "\u7b2c 182 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 182", "contest_title_slug": "weekly-contest-182", "contest_id": 166, "contest_start_time": 1585449000, "contest_duration": 5400, "user_num": 3911, "question_slugs": ["find-lucky-integer-in-an-array", "count-number-of-teams", "design-underground-system", "find-all-good-strings"]}, {"contest_title": "\u7b2c 183 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 183", "contest_title_slug": "weekly-contest-183", "contest_id": 168, "contest_start_time": 1586053800, "contest_duration": 5400, "user_num": 3756, "question_slugs": ["minimum-subsequence-in-non-increasing-order", "number-of-steps-to-reduce-a-number-in-binary-representation-to-one", "longest-happy-string", "stone-game-iii"]}, {"contest_title": "\u7b2c 184 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 184", "contest_title_slug": "weekly-contest-184", "contest_id": 175, "contest_start_time": 1586658600, "contest_duration": 5400, "user_num": 3847, "question_slugs": ["string-matching-in-an-array", "queries-on-a-permutation-with-key", "html-entity-parser", "number-of-ways-to-paint-n-3-grid"]}, {"contest_title": "\u7b2c 185 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 185", "contest_title_slug": "weekly-contest-185", "contest_id": 177, "contest_start_time": 1587263400, "contest_duration": 5400, "user_num": 5004, "question_slugs": ["reformat-the-string", "display-table-of-food-orders-in-a-restaurant", "minimum-number-of-frogs-croaking", "build-array-where-you-can-find-the-maximum-exactly-k-comparisons"]}, {"contest_title": "\u7b2c 186 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 186", "contest_title_slug": "weekly-contest-186", "contest_id": 185, "contest_start_time": 1587868200, "contest_duration": 5400, "user_num": 3108, "question_slugs": ["maximum-score-after-splitting-a-string", "maximum-points-you-can-obtain-from-cards", "diagonal-traverse-ii", "constrained-subsequence-sum"]}, {"contest_title": "\u7b2c 187 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 187", "contest_title_slug": "weekly-contest-187", "contest_id": 191, "contest_start_time": 1588473000, "contest_duration": 5400, "user_num": 3109, "question_slugs": ["destination-city", "check-if-all-1s-are-at-least-length-k-places-away", "longest-continuous-subarray-with-absolute-diff-less-than-or-equal-to-limit", "find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows"]}, {"contest_title": "\u7b2c 188 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 188", "contest_title_slug": "weekly-contest-188", "contest_id": 195, "contest_start_time": 1589077800, "contest_duration": 5400, "user_num": 3982, "question_slugs": ["build-an-array-with-stack-operations", "count-triplets-that-can-form-two-arrays-of-equal-xor", "minimum-time-to-collect-all-apples-in-a-tree", "number-of-ways-of-cutting-a-pizza"]}, {"contest_title": "\u7b2c 189 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 189", "contest_title_slug": "weekly-contest-189", "contest_id": 197, "contest_start_time": 1589682600, "contest_duration": 5400, "user_num": 3692, "question_slugs": ["number-of-students-doing-homework-at-a-given-time", "rearrange-words-in-a-sentence", "people-whose-list-of-favorite-companies-is-not-a-subset-of-another-list", "maximum-number-of-darts-inside-of-a-circular-dartboard"]}, {"contest_title": "\u7b2c 190 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 190", "contest_title_slug": "weekly-contest-190", "contest_id": 201, "contest_start_time": 1590287400, "contest_duration": 5400, "user_num": 3352, "question_slugs": ["check-if-a-word-occurs-as-a-prefix-of-any-word-in-a-sentence", "maximum-number-of-vowels-in-a-substring-of-given-length", "pseudo-palindromic-paths-in-a-binary-tree", "max-dot-product-of-two-subsequences"]}, {"contest_title": "\u7b2c 191 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 191", "contest_title_slug": "weekly-contest-191", "contest_id": 203, "contest_start_time": 1590892200, "contest_duration": 5400, "user_num": 3687, "question_slugs": ["maximum-product-of-two-elements-in-an-array", "maximum-area-of-a-piece-of-cake-after-horizontal-and-vertical-cuts", "reorder-routes-to-make-all-paths-lead-to-the-city-zero", "probability-of-a-two-boxes-having-the-same-number-of-distinct-balls"]}, {"contest_title": "\u7b2c 192 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 192", "contest_title_slug": "weekly-contest-192", "contest_id": 207, "contest_start_time": 1591497000, "contest_duration": 5400, "user_num": 3615, "question_slugs": ["shuffle-the-array", "the-k-strongest-values-in-an-array", "design-browser-history", "paint-house-iii"]}, {"contest_title": "\u7b2c 193 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 193", "contest_title_slug": "weekly-contest-193", "contest_id": 209, "contest_start_time": 1592101800, "contest_duration": 5400, "user_num": 3804, "question_slugs": ["running-sum-of-1d-array", "least-number-of-unique-integers-after-k-removals", "minimum-number-of-days-to-make-m-bouquets", "kth-ancestor-of-a-tree-node"]}, {"contest_title": "\u7b2c 194 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 194", "contest_title_slug": "weekly-contest-194", "contest_id": 213, "contest_start_time": 1592706600, "contest_duration": 5400, "user_num": 4378, "question_slugs": ["xor-operation-in-an-array", "making-file-names-unique", "avoid-flood-in-the-city", "find-critical-and-pseudo-critical-edges-in-minimum-spanning-tree"]}, {"contest_title": "\u7b2c 195 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 195", "contest_title_slug": "weekly-contest-195", "contest_id": 215, "contest_start_time": 1593311400, "contest_duration": 5400, "user_num": 3401, "question_slugs": ["path-crossing", "check-if-array-pairs-are-divisible-by-k", "number-of-subsequences-that-satisfy-the-given-sum-condition", "max-value-of-equation"]}, {"contest_title": "\u7b2c 196 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 196", "contest_title_slug": "weekly-contest-196", "contest_id": 219, "contest_start_time": 1593916200, "contest_duration": 5400, "user_num": 5507, "question_slugs": ["can-make-arithmetic-progression-from-sequence", "last-moment-before-all-ants-fall-out-of-a-plank", "count-submatrices-with-all-ones", "minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits"]}, {"contest_title": "\u7b2c 197 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 197", "contest_title_slug": "weekly-contest-197", "contest_id": 221, "contest_start_time": 1594521000, "contest_duration": 5400, "user_num": 5275, "question_slugs": ["number-of-good-pairs", "number-of-substrings-with-only-1s", "path-with-maximum-probability", "best-position-for-a-service-centre"]}, {"contest_title": "\u7b2c 198 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 198", "contest_title_slug": "weekly-contest-198", "contest_id": 226, "contest_start_time": 1595125800, "contest_duration": 5400, "user_num": 5780, "question_slugs": ["water-bottles", "number-of-nodes-in-the-sub-tree-with-the-same-label", "maximum-number-of-non-overlapping-substrings", "find-a-value-of-a-mysterious-function-closest-to-target"]}, {"contest_title": "\u7b2c 199 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 199", "contest_title_slug": "weekly-contest-199", "contest_id": 228, "contest_start_time": 1595730600, "contest_duration": 5400, "user_num": 5232, "question_slugs": ["shuffle-string", "minimum-suffix-flips", "number-of-good-leaf-nodes-pairs", "string-compression-ii"]}, {"contest_title": "\u7b2c 200 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 200", "contest_title_slug": "weekly-contest-200", "contest_id": 235, "contest_start_time": 1596335400, "contest_duration": 5400, "user_num": 5476, "question_slugs": ["count-good-triplets", "find-the-winner-of-an-array-game", "minimum-swaps-to-arrange-a-binary-grid", "get-the-maximum-score"]}, {"contest_title": "\u7b2c 201 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 201", "contest_title_slug": "weekly-contest-201", "contest_id": 238, "contest_start_time": 1596940200, "contest_duration": 5400, "user_num": 5615, "question_slugs": ["make-the-string-great", "find-kth-bit-in-nth-binary-string", "maximum-number-of-non-overlapping-subarrays-with-sum-equals-target", "minimum-cost-to-cut-a-stick"]}, {"contest_title": "\u7b2c 202 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 202", "contest_title_slug": "weekly-contest-202", "contest_id": 242, "contest_start_time": 1597545000, "contest_duration": 5400, "user_num": 4990, "question_slugs": ["three-consecutive-odds", "minimum-operations-to-make-array-equal", "magnetic-force-between-two-balls", "minimum-number-of-days-to-eat-n-oranges"]}, {"contest_title": "\u7b2c 203 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 203", "contest_title_slug": "weekly-contest-203", "contest_id": 244, "contest_start_time": 1598149800, "contest_duration": 5400, "user_num": 5285, "question_slugs": ["most-visited-sector-in-a-circular-track", "maximum-number-of-coins-you-can-get", "find-latest-group-of-size-m", "stone-game-v"]}, {"contest_title": "\u7b2c 204 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 204", "contest_title_slug": "weekly-contest-204", "contest_id": 257, "contest_start_time": 1598754600, "contest_duration": 5400, "user_num": 4487, "question_slugs": ["detect-pattern-of-length-m-repeated-k-or-more-times", "maximum-length-of-subarray-with-positive-product", "minimum-number-of-days-to-disconnect-island", "number-of-ways-to-reorder-array-to-get-same-bst"]}, {"contest_title": "\u7b2c 205 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 205", "contest_title_slug": "weekly-contest-205", "contest_id": 260, "contest_start_time": 1599359400, "contest_duration": 5400, "user_num": 4176, "question_slugs": ["replace-all-s-to-avoid-consecutive-repeating-characters", "number-of-ways-where-square-of-number-is-equal-to-product-of-two-numbers", "minimum-time-to-make-rope-colorful", "remove-max-number-of-edges-to-keep-graph-fully-traversable"]}, {"contest_title": "\u7b2c 206 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 206", "contest_title_slug": "weekly-contest-206", "contest_id": 267, "contest_start_time": 1599964200, "contest_duration": 5400, "user_num": 4493, "question_slugs": ["special-positions-in-a-binary-matrix", "count-unhappy-friends", "min-cost-to-connect-all-points", "check-if-string-is-transformable-with-substring-sort-operations"]}, {"contest_title": "\u7b2c 207 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 207", "contest_title_slug": "weekly-contest-207", "contest_id": 278, "contest_start_time": 1600569000, "contest_duration": 5400, "user_num": 4116, "question_slugs": ["rearrange-spaces-between-words", "split-a-string-into-the-max-number-of-unique-substrings", "maximum-non-negative-product-in-a-matrix", "minimum-cost-to-connect-two-groups-of-points"]}, {"contest_title": "\u7b2c 208 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 208", "contest_title_slug": "weekly-contest-208", "contest_id": 289, "contest_start_time": 1601173800, "contest_duration": 5400, "user_num": 3582, "question_slugs": ["crawler-log-folder", "maximum-profit-of-operating-a-centennial-wheel", "throne-inheritance", "maximum-number-of-achievable-transfer-requests"]}, {"contest_title": "\u7b2c 209 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 209", "contest_title_slug": "weekly-contest-209", "contest_id": 291, "contest_start_time": 1601778600, "contest_duration": 5400, "user_num": 4023, "question_slugs": ["special-array-with-x-elements-greater-than-or-equal-x", "even-odd-tree", "maximum-number-of-visible-points", "minimum-one-bit-operations-to-make-integers-zero"]}, {"contest_title": "\u7b2c 210 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 210", "contest_title_slug": "weekly-contest-210", "contest_id": 295, "contest_start_time": 1602383400, "contest_duration": 5400, "user_num": 4007, "question_slugs": ["maximum-nesting-depth-of-the-parentheses", "maximal-network-rank", "split-two-strings-to-make-palindrome", "count-subtrees-with-max-distance-between-cities"]}, {"contest_title": "\u7b2c 211 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 211", "contest_title_slug": "weekly-contest-211", "contest_id": 297, "contest_start_time": 1602988200, "contest_duration": 5400, "user_num": 4034, "question_slugs": ["largest-substring-between-two-equal-characters", "lexicographically-smallest-string-after-applying-operations", "best-team-with-no-conflicts", "graph-connectivity-with-threshold"]}, {"contest_title": "\u7b2c 212 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 212", "contest_title_slug": "weekly-contest-212", "contest_id": 301, "contest_start_time": 1603593000, "contest_duration": 5400, "user_num": 4227, "question_slugs": ["slowest-key", "arithmetic-subarrays", "path-with-minimum-effort", "rank-transform-of-a-matrix"]}, {"contest_title": "\u7b2c 213 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 213", "contest_title_slug": "weekly-contest-213", "contest_id": 303, "contest_start_time": 1604197800, "contest_duration": 5400, "user_num": 3827, "question_slugs": ["check-array-formation-through-concatenation", "count-sorted-vowel-strings", "furthest-building-you-can-reach", "kth-smallest-instructions"]}, {"contest_title": "\u7b2c 214 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 214", "contest_title_slug": "weekly-contest-214", "contest_id": 307, "contest_start_time": 1604802600, "contest_duration": 5400, "user_num": 3598, "question_slugs": ["get-maximum-in-generated-array", "minimum-deletions-to-make-character-frequencies-unique", "sell-diminishing-valued-colored-balls", "create-sorted-array-through-instructions"]}, {"contest_title": "\u7b2c 215 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 215", "contest_title_slug": "weekly-contest-215", "contest_id": 309, "contest_start_time": 1605407400, "contest_duration": 5400, "user_num": 4429, "question_slugs": ["design-an-ordered-stream", "determine-if-two-strings-are-close", "minimum-operations-to-reduce-x-to-zero", "maximize-grid-happiness"]}, {"contest_title": "\u7b2c 216 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 216", "contest_title_slug": "weekly-contest-216", "contest_id": 313, "contest_start_time": 1606012200, "contest_duration": 5400, "user_num": 3857, "question_slugs": ["check-if-two-string-arrays-are-equivalent", "smallest-string-with-a-given-numeric-value", "ways-to-make-a-fair-array", "minimum-initial-energy-to-finish-tasks"]}, {"contest_title": "\u7b2c 217 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 217", "contest_title_slug": "weekly-contest-217", "contest_id": 315, "contest_start_time": 1606617000, "contest_duration": 5400, "user_num": 3745, "question_slugs": ["richest-customer-wealth", "find-the-most-competitive-subsequence", "minimum-moves-to-make-array-complementary", "minimize-deviation-in-array"]}, {"contest_title": "\u7b2c 218 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 218", "contest_title_slug": "weekly-contest-218", "contest_id": 319, "contest_start_time": 1607221800, "contest_duration": 5400, "user_num": 3762, "question_slugs": ["goal-parser-interpretation", "max-number-of-k-sum-pairs", "concatenation-of-consecutive-binary-numbers", "minimum-incompatibility"]}, {"contest_title": "\u7b2c 219 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 219", "contest_title_slug": "weekly-contest-219", "contest_id": 322, "contest_start_time": 1607826600, "contest_duration": 5400, "user_num": 3710, "question_slugs": ["count-of-matches-in-tournament", "partitioning-into-minimum-number-of-deci-binary-numbers", "stone-game-vii", "maximum-height-by-stacking-cuboids"]}, {"contest_title": "\u7b2c 220 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 220", "contest_title_slug": "weekly-contest-220", "contest_id": 326, "contest_start_time": 1608431400, "contest_duration": 5400, "user_num": 3691, "question_slugs": ["reformat-phone-number", "maximum-erasure-value", "jump-game-vi", "checking-existence-of-edge-length-limited-paths"]}, {"contest_title": "\u7b2c 221 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 221", "contest_title_slug": "weekly-contest-221", "contest_id": 328, "contest_start_time": 1609036200, "contest_duration": 5400, "user_num": 3398, "question_slugs": ["determine-if-string-halves-are-alike", "maximum-number-of-eaten-apples", "where-will-the-ball-fall", "maximum-xor-with-an-element-from-array"]}, {"contest_title": "\u7b2c 222 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 222", "contest_title_slug": "weekly-contest-222", "contest_id": 332, "contest_start_time": 1609641000, "contest_duration": 5400, "user_num": 3119, "question_slugs": ["maximum-units-on-a-truck", "count-good-meals", "ways-to-split-array-into-three-subarrays", "minimum-operations-to-make-a-subsequence"]}, {"contest_title": "\u7b2c 223 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 223", "contest_title_slug": "weekly-contest-223", "contest_id": 334, "contest_start_time": 1610245800, "contest_duration": 5400, "user_num": 3872, "question_slugs": ["decode-xored-array", "swapping-nodes-in-a-linked-list", "minimize-hamming-distance-after-swap-operations", "find-minimum-time-to-finish-all-jobs"]}, {"contest_title": "\u7b2c 224 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 224", "contest_title_slug": "weekly-contest-224", "contest_id": 338, "contest_start_time": 1610850600, "contest_duration": 5400, "user_num": 3795, "question_slugs": ["number-of-rectangles-that-can-form-the-largest-square", "tuple-with-same-product", "largest-submatrix-with-rearrangements", "cat-and-mouse-ii"]}, {"contest_title": "\u7b2c 225 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 225", "contest_title_slug": "weekly-contest-225", "contest_id": 340, "contest_start_time": 1611455400, "contest_duration": 5400, "user_num": 3853, "question_slugs": ["latest-time-by-replacing-hidden-digits", "change-minimum-characters-to-satisfy-one-of-three-conditions", "find-kth-largest-xor-coordinate-value", "building-boxes"]}, {"contest_title": "\u7b2c 226 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 226", "contest_title_slug": "weekly-contest-226", "contest_id": 344, "contest_start_time": 1612060200, "contest_duration": 5400, "user_num": 4034, "question_slugs": ["maximum-number-of-balls-in-a-box", "restore-the-array-from-adjacent-pairs", "can-you-eat-your-favorite-candy-on-your-favorite-day", "palindrome-partitioning-iv"]}, {"contest_title": "\u7b2c 227 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 227", "contest_title_slug": "weekly-contest-227", "contest_id": 346, "contest_start_time": 1612665000, "contest_duration": 5400, "user_num": 3546, "question_slugs": ["check-if-array-is-sorted-and-rotated", "maximum-score-from-removing-stones", "largest-merge-of-two-strings", "closest-subsequence-sum"]}, {"contest_title": "\u7b2c 228 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 228", "contest_title_slug": "weekly-contest-228", "contest_id": 350, "contest_start_time": 1613269800, "contest_duration": 5400, "user_num": 2484, "question_slugs": ["minimum-changes-to-make-alternating-binary-string", "count-number-of-homogenous-substrings", "minimum-limit-of-balls-in-a-bag", "minimum-degree-of-a-connected-trio-in-a-graph"]}, {"contest_title": "\u7b2c 229 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 229", "contest_title_slug": "weekly-contest-229", "contest_id": 352, "contest_start_time": 1613874600, "contest_duration": 5400, "user_num": 3484, "question_slugs": ["merge-strings-alternately", "minimum-number-of-operations-to-move-all-balls-to-each-box", "maximum-score-from-performing-multiplication-operations", "maximize-palindrome-length-from-subsequences"]}, {"contest_title": "\u7b2c 230 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 230", "contest_title_slug": "weekly-contest-230", "contest_id": 356, "contest_start_time": 1614479400, "contest_duration": 5400, "user_num": 3728, "question_slugs": ["count-items-matching-a-rule", "closest-dessert-cost", "equal-sum-arrays-with-minimum-number-of-operations", "car-fleet-ii"]}, {"contest_title": "\u7b2c 231 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 231", "contest_title_slug": "weekly-contest-231", "contest_id": 358, "contest_start_time": 1615084200, "contest_duration": 5400, "user_num": 4668, "question_slugs": ["check-if-binary-string-has-at-most-one-segment-of-ones", "minimum-elements-to-add-to-form-a-given-sum", "number-of-restricted-paths-from-first-to-last-node", "make-the-xor-of-all-segments-equal-to-zero"]}, {"contest_title": "\u7b2c 232 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 232", "contest_title_slug": "weekly-contest-232", "contest_id": 363, "contest_start_time": 1615689000, "contest_duration": 5400, "user_num": 4802, "question_slugs": ["check-if-one-string-swap-can-make-strings-equal", "find-center-of-star-graph", "maximum-average-pass-ratio", "maximum-score-of-a-good-subarray"]}, {"contest_title": "\u7b2c 233 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 233", "contest_title_slug": "weekly-contest-233", "contest_id": 371, "contest_start_time": 1616293800, "contest_duration": 5400, "user_num": 5010, "question_slugs": ["maximum-ascending-subarray-sum", "number-of-orders-in-the-backlog", "maximum-value-at-a-given-index-in-a-bounded-array", "count-pairs-with-xor-in-a-range"]}, {"contest_title": "\u7b2c 234 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 234", "contest_title_slug": "weekly-contest-234", "contest_id": 375, "contest_start_time": 1616898600, "contest_duration": 5400, "user_num": 4998, "question_slugs": ["number-of-different-integers-in-a-string", "minimum-number-of-operations-to-reinitialize-a-permutation", "evaluate-the-bracket-pairs-of-a-string", "maximize-number-of-nice-divisors"]}, {"contest_title": "\u7b2c 235 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 235", "contest_title_slug": "weekly-contest-235", "contest_id": 377, "contest_start_time": 1617503400, "contest_duration": 5400, "user_num": 4494, "question_slugs": ["truncate-sentence", "finding-the-users-active-minutes", "minimum-absolute-sum-difference", "number-of-different-subsequences-gcds"]}, {"contest_title": "\u7b2c 236 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 236", "contest_title_slug": "weekly-contest-236", "contest_id": 391, "contest_start_time": 1618108200, "contest_duration": 5400, "user_num": 5113, "question_slugs": ["sign-of-the-product-of-an-array", "find-the-winner-of-the-circular-game", "minimum-sideway-jumps", "finding-mk-average"]}, {"contest_title": "\u7b2c 237 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 237", "contest_title_slug": "weekly-contest-237", "contest_id": 393, "contest_start_time": 1618713000, "contest_duration": 5400, "user_num": 4577, "question_slugs": ["check-if-the-sentence-is-pangram", "maximum-ice-cream-bars", "single-threaded-cpu", "find-xor-sum-of-all-pairs-bitwise-and"]}, {"contest_title": "\u7b2c 238 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 238", "contest_title_slug": "weekly-contest-238", "contest_id": 397, "contest_start_time": 1619317800, "contest_duration": 5400, "user_num": 3978, "question_slugs": ["sum-of-digits-in-base-k", "frequency-of-the-most-frequent-element", "longest-substring-of-all-vowels-in-order", "maximum-building-height"]}, {"contest_title": "\u7b2c 239 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 239", "contest_title_slug": "weekly-contest-239", "contest_id": 399, "contest_start_time": 1619922600, "contest_duration": 5400, "user_num": 3907, "question_slugs": ["minimum-distance-to-the-target-element", "splitting-a-string-into-descending-consecutive-values", "minimum-adjacent-swaps-to-reach-the-kth-smallest-number", "minimum-interval-to-include-each-query"]}, {"contest_title": "\u7b2c 240 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 240", "contest_title_slug": "weekly-contest-240", "contest_id": 403, "contest_start_time": 1620527400, "contest_duration": 5400, "user_num": 4307, "question_slugs": ["maximum-population-year", "maximum-distance-between-a-pair-of-values", "maximum-subarray-min-product", "largest-color-value-in-a-directed-graph"]}, {"contest_title": "\u7b2c 241 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 241", "contest_title_slug": "weekly-contest-241", "contest_id": 405, "contest_start_time": 1621132200, "contest_duration": 5400, "user_num": 4491, "question_slugs": ["sum-of-all-subset-xor-totals", "minimum-number-of-swaps-to-make-the-binary-string-alternating", "finding-pairs-with-a-certain-sum", "number-of-ways-to-rearrange-sticks-with-k-sticks-visible"]}, {"contest_title": "\u7b2c 242 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 242", "contest_title_slug": "weekly-contest-242", "contest_id": 409, "contest_start_time": 1621737000, "contest_duration": 5400, "user_num": 4306, "question_slugs": ["longer-contiguous-segments-of-ones-than-zeros", "minimum-speed-to-arrive-on-time", "jump-game-vii", "stone-game-viii"]}, {"contest_title": "\u7b2c 243 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 243", "contest_title_slug": "weekly-contest-243", "contest_id": 411, "contest_start_time": 1622341800, "contest_duration": 5400, "user_num": 4493, "question_slugs": ["check-if-word-equals-summation-of-two-words", "maximum-value-after-insertion", "process-tasks-using-servers", "minimum-skips-to-arrive-at-meeting-on-time"]}, {"contest_title": "\u7b2c 244 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 244", "contest_title_slug": "weekly-contest-244", "contest_id": 415, "contest_start_time": 1622946600, "contest_duration": 5400, "user_num": 4430, "question_slugs": ["determine-whether-matrix-can-be-obtained-by-rotation", "reduction-operations-to-make-the-array-elements-equal", "minimum-number-of-flips-to-make-the-binary-string-alternating", "minimum-space-wasted-from-packaging"]}, {"contest_title": "\u7b2c 245 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 245", "contest_title_slug": "weekly-contest-245", "contest_id": 417, "contest_start_time": 1623551400, "contest_duration": 5400, "user_num": 4271, "question_slugs": ["redistribute-characters-to-make-all-strings-equal", "maximum-number-of-removable-characters", "merge-triplets-to-form-target-triplet", "the-earliest-and-latest-rounds-where-players-compete"]}, {"contest_title": "\u7b2c 246 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 246", "contest_title_slug": "weekly-contest-246", "contest_id": 422, "contest_start_time": 1624156200, "contest_duration": 5400, "user_num": 4136, "question_slugs": ["largest-odd-number-in-string", "the-number-of-full-rounds-you-have-played", "count-sub-islands", "minimum-absolute-difference-queries"]}, {"contest_title": "\u7b2c 247 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 247", "contest_title_slug": "weekly-contest-247", "contest_id": 426, "contest_start_time": 1624761000, "contest_duration": 5400, "user_num": 3981, "question_slugs": ["maximum-product-difference-between-two-pairs", "cyclically-rotating-a-grid", "number-of-wonderful-substrings", "count-ways-to-build-rooms-in-an-ant-colony"]}, {"contest_title": "\u7b2c 248 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 248", "contest_title_slug": "weekly-contest-248", "contest_id": 430, "contest_start_time": 1625365800, "contest_duration": 5400, "user_num": 4451, "question_slugs": ["build-array-from-permutation", "eliminate-maximum-number-of-monsters", "count-good-numbers", "longest-common-subpath"]}, {"contest_title": "\u7b2c 249 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 249", "contest_title_slug": "weekly-contest-249", "contest_id": 432, "contest_start_time": 1625970600, "contest_duration": 5400, "user_num": 4335, "question_slugs": ["concatenation-of-array", "unique-length-3-palindromic-subsequences", "painting-a-grid-with-three-different-colors", "merge-bsts-to-create-single-bst"]}, {"contest_title": "\u7b2c 250 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 250", "contest_title_slug": "weekly-contest-250", "contest_id": 436, "contest_start_time": 1626575400, "contest_duration": 5400, "user_num": 4315, "question_slugs": ["maximum-number-of-words-you-can-type", "add-minimum-number-of-rungs", "maximum-number-of-points-with-cost", "maximum-genetic-difference-query"]}, {"contest_title": "\u7b2c 251 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 251", "contest_title_slug": "weekly-contest-251", "contest_id": 438, "contest_start_time": 1627180200, "contest_duration": 5400, "user_num": 4747, "question_slugs": ["sum-of-digits-of-string-after-convert", "largest-number-after-mutating-substring", "maximum-compatibility-score-sum", "delete-duplicate-folders-in-system"]}, {"contest_title": "\u7b2c 252 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 252", "contest_title_slug": "weekly-contest-252", "contest_id": 442, "contest_start_time": 1627785000, "contest_duration": 5400, "user_num": 4647, "question_slugs": ["three-divisors", "maximum-number-of-weeks-for-which-you-can-work", "minimum-garden-perimeter-to-collect-enough-apples", "count-number-of-special-subsequences"]}, {"contest_title": "\u7b2c 253 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 253", "contest_title_slug": "weekly-contest-253", "contest_id": 444, "contest_start_time": 1628389800, "contest_duration": 5400, "user_num": 4570, "question_slugs": ["check-if-string-is-a-prefix-of-array", "remove-stones-to-minimize-the-total", "minimum-number-of-swaps-to-make-the-string-balanced", "find-the-longest-valid-obstacle-course-at-each-position"]}, {"contest_title": "\u7b2c 254 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 254", "contest_title_slug": "weekly-contest-254", "contest_id": 449, "contest_start_time": 1628994600, "contest_duration": 5400, "user_num": 4349, "question_slugs": ["number-of-strings-that-appear-as-substrings-in-word", "array-with-elements-not-equal-to-average-of-neighbors", "minimum-non-zero-product-of-the-array-elements", "last-day-where-you-can-still-cross"]}, {"contest_title": "\u7b2c 255 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 255", "contest_title_slug": "weekly-contest-255", "contest_id": 457, "contest_start_time": 1629599400, "contest_duration": 5400, "user_num": 4333, "question_slugs": ["find-greatest-common-divisor-of-array", "find-unique-binary-string", "minimize-the-difference-between-target-and-chosen-elements", "find-array-given-subset-sums"]}, {"contest_title": "\u7b2c 256 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 256", "contest_title_slug": "weekly-contest-256", "contest_id": 462, "contest_start_time": 1630204200, "contest_duration": 5400, "user_num": 4136, "question_slugs": ["minimum-difference-between-highest-and-lowest-of-k-scores", "find-the-kth-largest-integer-in-the-array", "minimum-number-of-work-sessions-to-finish-the-tasks", "number-of-unique-good-subsequences"]}, {"contest_title": "\u7b2c 257 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 257", "contest_title_slug": "weekly-contest-257", "contest_id": 464, "contest_start_time": 1630809000, "contest_duration": 5400, "user_num": 4278, "question_slugs": ["count-special-quadruplets", "the-number-of-weak-characters-in-the-game", "first-day-where-you-have-been-in-all-the-rooms", "gcd-sort-of-an-array"]}, {"contest_title": "\u7b2c 258 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 258", "contest_title_slug": "weekly-contest-258", "contest_id": 468, "contest_start_time": 1631413800, "contest_duration": 5400, "user_num": 4519, "question_slugs": ["reverse-prefix-of-word", "number-of-pairs-of-interchangeable-rectangles", "maximum-product-of-the-length-of-two-palindromic-subsequences", "smallest-missing-genetic-value-in-each-subtree"]}, {"contest_title": "\u7b2c 259 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 259", "contest_title_slug": "weekly-contest-259", "contest_id": 474, "contest_start_time": 1632018600, "contest_duration": 5400, "user_num": 3775, "question_slugs": ["final-value-of-variable-after-performing-operations", "sum-of-beauty-in-the-array", "detect-squares", "longest-subsequence-repeated-k-times"]}, {"contest_title": "\u7b2c 260 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 260", "contest_title_slug": "weekly-contest-260", "contest_id": 478, "contest_start_time": 1632623400, "contest_duration": 5400, "user_num": 3654, "question_slugs": ["maximum-difference-between-increasing-elements", "grid-game", "check-if-word-can-be-placed-in-crossword", "the-score-of-students-solving-math-expression"]}, {"contest_title": "\u7b2c 261 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 261", "contest_title_slug": "weekly-contest-261", "contest_id": 481, "contest_start_time": 1633228200, "contest_duration": 5400, "user_num": 3368, "question_slugs": ["minimum-moves-to-convert-string", "find-missing-observations", "stone-game-ix", "smallest-k-length-subsequence-with-occurrences-of-a-letter"]}, {"contest_title": "\u7b2c 262 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 262", "contest_title_slug": "weekly-contest-262", "contest_id": 485, "contest_start_time": 1633833000, "contest_duration": 5400, "user_num": 4261, "question_slugs": ["two-out-of-three", "minimum-operations-to-make-a-uni-value-grid", "stock-price-fluctuation", "partition-array-into-two-arrays-to-minimize-sum-difference"]}, {"contest_title": "\u7b2c 263 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 263", "contest_title_slug": "weekly-contest-263", "contest_id": 487, "contest_start_time": 1634437800, "contest_duration": 5400, "user_num": 4572, "question_slugs": ["check-if-numbers-are-ascending-in-a-sentence", "simple-bank-system", "count-number-of-maximum-bitwise-or-subsets", "second-minimum-time-to-reach-destination"]}, {"contest_title": "\u7b2c 264 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 264", "contest_title_slug": "weekly-contest-264", "contest_id": 491, "contest_start_time": 1635042600, "contest_duration": 5400, "user_num": 4659, "question_slugs": ["number-of-valid-words-in-a-sentence", "next-greater-numerically-balanced-number", "count-nodes-with-the-highest-score", "parallel-courses-iii"]}, {"contest_title": "\u7b2c 265 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 265", "contest_title_slug": "weekly-contest-265", "contest_id": 493, "contest_start_time": 1635647400, "contest_duration": 5400, "user_num": 4182, "question_slugs": ["smallest-index-with-equal-value", "find-the-minimum-and-maximum-number-of-nodes-between-critical-points", "minimum-operations-to-convert-number", "check-if-an-original-string-exists-given-two-encoded-strings"]}, {"contest_title": "\u7b2c 266 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 266", "contest_title_slug": "weekly-contest-266", "contest_id": 498, "contest_start_time": 1636252200, "contest_duration": 5400, "user_num": 4385, "question_slugs": ["count-vowel-substrings-of-a-string", "vowels-of-all-substrings", "minimized-maximum-of-products-distributed-to-any-store", "maximum-path-quality-of-a-graph"]}, {"contest_title": "\u7b2c 267 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 267", "contest_title_slug": "weekly-contest-267", "contest_id": 500, "contest_start_time": 1636857000, "contest_duration": 5400, "user_num": 4365, "question_slugs": ["time-needed-to-buy-tickets", "reverse-nodes-in-even-length-groups", "decode-the-slanted-ciphertext", "process-restricted-friend-requests"]}, {"contest_title": "\u7b2c 268 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 268", "contest_title_slug": "weekly-contest-268", "contest_id": 504, "contest_start_time": 1637461800, "contest_duration": 5400, "user_num": 4398, "question_slugs": ["two-furthest-houses-with-different-colors", "watering-plants", "range-frequency-queries", "sum-of-k-mirror-numbers"]}, {"contest_title": "\u7b2c 269 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 269", "contest_title_slug": "weekly-contest-269", "contest_id": 506, "contest_start_time": 1638066600, "contest_duration": 5400, "user_num": 4293, "question_slugs": ["find-target-indices-after-sorting-array", "k-radius-subarray-averages", "removing-minimum-and-maximum-from-array", "find-all-people-with-secret"]}, {"contest_title": "\u7b2c 270 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 270", "contest_title_slug": "weekly-contest-270", "contest_id": 510, "contest_start_time": 1638671400, "contest_duration": 5400, "user_num": 4748, "question_slugs": ["finding-3-digit-even-numbers", "delete-the-middle-node-of-a-linked-list", "step-by-step-directions-from-a-binary-tree-node-to-another", "valid-arrangement-of-pairs"]}, {"contest_title": "\u7b2c 271 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 271", "contest_title_slug": "weekly-contest-271", "contest_id": 512, "contest_start_time": 1639276200, "contest_duration": 5400, "user_num": 4562, "question_slugs": ["rings-and-rods", "sum-of-subarray-ranges", "watering-plants-ii", "maximum-fruits-harvested-after-at-most-k-steps"]}, {"contest_title": "\u7b2c 272 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 272", "contest_title_slug": "weekly-contest-272", "contest_id": 516, "contest_start_time": 1639881000, "contest_duration": 5400, "user_num": 4698, "question_slugs": ["find-first-palindromic-string-in-the-array", "adding-spaces-to-a-string", "number-of-smooth-descent-periods-of-a-stock", "minimum-operations-to-make-the-array-k-increasing"]}, {"contest_title": "\u7b2c 273 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 273", "contest_title_slug": "weekly-contest-273", "contest_id": 518, "contest_start_time": 1640485800, "contest_duration": 5400, "user_num": 4368, "question_slugs": ["a-number-after-a-double-reversal", "execution-of-all-suffix-instructions-staying-in-a-grid", "intervals-between-identical-elements", "recover-the-original-array"]}, {"contest_title": "\u7b2c 274 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 274", "contest_title_slug": "weekly-contest-274", "contest_id": 522, "contest_start_time": 1641090600, "contest_duration": 5400, "user_num": 4109, "question_slugs": ["check-if-all-as-appears-before-all-bs", "number-of-laser-beams-in-a-bank", "destroying-asteroids", "maximum-employees-to-be-invited-to-a-meeting"]}, {"contest_title": "\u7b2c 275 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 275", "contest_title_slug": "weekly-contest-275", "contest_id": 524, "contest_start_time": 1641695400, "contest_duration": 5400, "user_num": 4787, "question_slugs": ["check-if-every-row-and-column-contains-all-numbers", "minimum-swaps-to-group-all-1s-together-ii", "count-words-obtained-after-adding-a-letter", "earliest-possible-day-of-full-bloom"]}, {"contest_title": "\u7b2c 276 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 276", "contest_title_slug": "weekly-contest-276", "contest_id": 528, "contest_start_time": 1642300200, "contest_duration": 5400, "user_num": 5244, "question_slugs": ["divide-a-string-into-groups-of-size-k", "minimum-moves-to-reach-target-score", "solving-questions-with-brainpower", "maximum-running-time-of-n-computers"]}, {"contest_title": "\u7b2c 277 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 277", "contest_title_slug": "weekly-contest-277", "contest_id": 530, "contest_start_time": 1642905000, "contest_duration": 5400, "user_num": 5060, "question_slugs": ["count-elements-with-strictly-smaller-and-greater-elements", "rearrange-array-elements-by-sign", "find-all-lonely-numbers-in-the-array", "maximum-good-people-based-on-statements"]}, {"contest_title": "\u7b2c 278 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 278", "contest_title_slug": "weekly-contest-278", "contest_id": 534, "contest_start_time": 1643509800, "contest_duration": 5400, "user_num": 4643, "question_slugs": ["keep-multiplying-found-values-by-two", "all-divisions-with-the-highest-score-of-a-binary-array", "find-substring-with-given-hash-value", "groups-of-strings"]}, {"contest_title": "\u7b2c 279 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 279", "contest_title_slug": "weekly-contest-279", "contest_id": 536, "contest_start_time": 1644114600, "contest_duration": 5400, "user_num": 4132, "question_slugs": ["sort-even-and-odd-indices-independently", "smallest-value-of-the-rearranged-number", "design-bitset", "minimum-time-to-remove-all-cars-containing-illegal-goods"]}, {"contest_title": "\u7b2c 280 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 280", "contest_title_slug": "weekly-contest-280", "contest_id": 540, "contest_start_time": 1644719400, "contest_duration": 5400, "user_num": 5834, "question_slugs": ["count-operations-to-obtain-zero", "minimum-operations-to-make-the-array-alternating", "removing-minimum-number-of-magic-beans", "maximum-and-sum-of-array"]}, {"contest_title": "\u7b2c 281 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 281", "contest_title_slug": "weekly-contest-281", "contest_id": 542, "contest_start_time": 1645324200, "contest_duration": 6000, "user_num": 6005, "question_slugs": ["count-integers-with-even-digit-sum", "merge-nodes-in-between-zeros", "construct-string-with-repeat-limit", "count-array-pairs-divisible-by-k"]}, {"contest_title": "\u7b2c 282 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 282", "contest_title_slug": "weekly-contest-282", "contest_id": 546, "contest_start_time": 1645929000, "contest_duration": 5400, "user_num": 7164, "question_slugs": ["counting-words-with-a-given-prefix", "minimum-number-of-steps-to-make-two-strings-anagram-ii", "minimum-time-to-complete-trips", "minimum-time-to-finish-the-race"]}, {"contest_title": "\u7b2c 283 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 283", "contest_title_slug": "weekly-contest-283", "contest_id": 551, "contest_start_time": 1646533800, "contest_duration": 5400, "user_num": 7817, "question_slugs": ["cells-in-a-range-on-an-excel-sheet", "append-k-integers-with-minimal-sum", "create-binary-tree-from-descriptions", "replace-non-coprime-numbers-in-array"]}, {"contest_title": "\u7b2c 284 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 284", "contest_title_slug": "weekly-contest-284", "contest_id": 555, "contest_start_time": 1647138600, "contest_duration": 5400, "user_num": 8483, "question_slugs": ["find-all-k-distant-indices-in-an-array", "count-artifacts-that-can-be-extracted", "maximize-the-topmost-element-after-k-moves", "minimum-weighted-subgraph-with-the-required-paths"]}, {"contest_title": "\u7b2c 285 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 285", "contest_title_slug": "weekly-contest-285", "contest_id": 558, "contest_start_time": 1647743400, "contest_duration": 5400, "user_num": 7501, "question_slugs": ["count-hills-and-valleys-in-an-array", "count-collisions-on-a-road", "maximum-points-in-an-archery-competition", "longest-substring-of-one-repeating-character"]}, {"contest_title": "\u7b2c 286 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 286", "contest_title_slug": "weekly-contest-286", "contest_id": 564, "contest_start_time": 1648348200, "contest_duration": 5400, "user_num": 7248, "question_slugs": ["find-the-difference-of-two-arrays", "minimum-deletions-to-make-array-beautiful", "find-palindrome-with-fixed-length", "maximum-value-of-k-coins-from-piles"]}, {"contest_title": "\u7b2c 287 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 287", "contest_title_slug": "weekly-contest-287", "contest_id": 569, "contest_start_time": 1648953000, "contest_duration": 5400, "user_num": 6811, "question_slugs": ["minimum-number-of-operations-to-convert-time", "find-players-with-zero-or-one-losses", "maximum-candies-allocated-to-k-children", "encrypt-and-decrypt-strings"]}, {"contest_title": "\u7b2c 288 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 288", "contest_title_slug": "weekly-contest-288", "contest_id": 573, "contest_start_time": 1649557800, "contest_duration": 5400, "user_num": 6926, "question_slugs": ["largest-number-after-digit-swaps-by-parity", "minimize-result-by-adding-parentheses-to-expression", "maximum-product-after-k-increments", "maximum-total-beauty-of-the-gardens"]}, {"contest_title": "\u7b2c 289 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 289", "contest_title_slug": "weekly-contest-289", "contest_id": 576, "contest_start_time": 1650162600, "contest_duration": 5400, "user_num": 7293, "question_slugs": ["calculate-digit-sum-of-a-string", "minimum-rounds-to-complete-all-tasks", "maximum-trailing-zeros-in-a-cornered-path", "longest-path-with-different-adjacent-characters"]}, {"contest_title": "\u7b2c 290 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 290", "contest_title_slug": "weekly-contest-290", "contest_id": 582, "contest_start_time": 1650767400, "contest_duration": 5400, "user_num": 6275, "question_slugs": ["intersection-of-multiple-arrays", "count-lattice-points-inside-a-circle", "count-number-of-rectangles-containing-each-point", "number-of-flowers-in-full-bloom"]}, {"contest_title": "\u7b2c 291 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 291", "contest_title_slug": "weekly-contest-291", "contest_id": 587, "contest_start_time": 1651372200, "contest_duration": 5400, "user_num": 6574, "question_slugs": ["remove-digit-from-number-to-maximize-result", "minimum-consecutive-cards-to-pick-up", "k-divisible-elements-subarrays", "total-appeal-of-a-string"]}, {"contest_title": "\u7b2c 292 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 292", "contest_title_slug": "weekly-contest-292", "contest_id": 591, "contest_start_time": 1651977000, "contest_duration": 5400, "user_num": 6884, "question_slugs": ["largest-3-same-digit-number-in-string", "count-nodes-equal-to-average-of-subtree", "count-number-of-texts", "check-if-there-is-a-valid-parentheses-string-path"]}, {"contest_title": "\u7b2c 293 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 293", "contest_title_slug": "weekly-contest-293", "contest_id": 593, "contest_start_time": 1652581800, "contest_duration": 5400, "user_num": 7357, "question_slugs": ["find-resultant-array-after-removing-anagrams", "maximum-consecutive-floors-without-special-floors", "largest-combination-with-bitwise-and-greater-than-zero", "count-integers-in-intervals"]}, {"contest_title": "\u7b2c 294 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 294", "contest_title_slug": "weekly-contest-294", "contest_id": 599, "contest_start_time": 1653186600, "contest_duration": 5400, "user_num": 6640, "question_slugs": ["percentage-of-letter-in-string", "maximum-bags-with-full-capacity-of-rocks", "minimum-lines-to-represent-a-line-chart", "sum-of-total-strength-of-wizards"]}, {"contest_title": "\u7b2c 295 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 295", "contest_title_slug": "weekly-contest-295", "contest_id": 605, "contest_start_time": 1653791400, "contest_duration": 5400, "user_num": 6447, "question_slugs": ["rearrange-characters-to-make-target-string", "apply-discount-to-prices", "steps-to-make-array-non-decreasing", "minimum-obstacle-removal-to-reach-corner"]}, {"contest_title": "\u7b2c 296 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 296", "contest_title_slug": "weekly-contest-296", "contest_id": 609, "contest_start_time": 1654396200, "contest_duration": 5400, "user_num": 5721, "question_slugs": ["min-max-game", "partition-array-such-that-maximum-difference-is-k", "replace-elements-in-an-array", "design-a-text-editor"]}, {"contest_title": "\u7b2c 297 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 297", "contest_title_slug": "weekly-contest-297", "contest_id": 611, "contest_start_time": 1655001000, "contest_duration": 5400, "user_num": 5915, "question_slugs": ["calculate-amount-paid-in-taxes", "minimum-path-cost-in-a-grid", "fair-distribution-of-cookies", "naming-a-company"]}, {"contest_title": "\u7b2c 298 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 298", "contest_title_slug": "weekly-contest-298", "contest_id": 615, "contest_start_time": 1655605800, "contest_duration": 5400, "user_num": 6228, "question_slugs": ["greatest-english-letter-in-upper-and-lower-case", "sum-of-numbers-with-units-digit-k", "longest-binary-subsequence-less-than-or-equal-to-k", "selling-pieces-of-wood"]}, {"contest_title": "\u7b2c 299 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 299", "contest_title_slug": "weekly-contest-299", "contest_id": 618, "contest_start_time": 1656210600, "contest_duration": 5400, "user_num": 6108, "question_slugs": ["check-if-matrix-is-x-matrix", "count-number-of-ways-to-place-houses", "maximum-score-of-spliced-array", "minimum-score-after-removals-on-a-tree"]}, {"contest_title": "\u7b2c 300 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 300", "contest_title_slug": "weekly-contest-300", "contest_id": 647, "contest_start_time": 1656815400, "contest_duration": 5400, "user_num": 6792, "question_slugs": ["decode-the-message", "spiral-matrix-iv", "number-of-people-aware-of-a-secret", "number-of-increasing-paths-in-a-grid"]}, {"contest_title": "\u7b2c 301 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 301", "contest_title_slug": "weekly-contest-301", "contest_id": 649, "contest_start_time": 1657420200, "contest_duration": 5400, "user_num": 7133, "question_slugs": ["minimum-amount-of-time-to-fill-cups", "smallest-number-in-infinite-set", "move-pieces-to-obtain-a-string", "count-the-number-of-ideal-arrays"]}, {"contest_title": "\u7b2c 302 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 302", "contest_title_slug": "weekly-contest-302", "contest_id": 653, "contest_start_time": 1658025000, "contest_duration": 5400, "user_num": 7092, "question_slugs": ["maximum-number-of-pairs-in-array", "max-sum-of-a-pair-with-equal-sum-of-digits", "query-kth-smallest-trimmed-number", "minimum-deletions-to-make-array-divisible"]}, {"contest_title": "\u7b2c 303 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 303", "contest_title_slug": "weekly-contest-303", "contest_id": 655, "contest_start_time": 1658629800, "contest_duration": 5400, "user_num": 7032, "question_slugs": ["first-letter-to-appear-twice", "equal-row-and-column-pairs", "design-a-food-rating-system", "number-of-excellent-pairs"]}, {"contest_title": "\u7b2c 304 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 304", "contest_title_slug": "weekly-contest-304", "contest_id": 659, "contest_start_time": 1659234600, "contest_duration": 5400, "user_num": 7372, "question_slugs": ["make-array-zero-by-subtracting-equal-amounts", "maximum-number-of-groups-entering-a-competition", "find-closest-node-to-given-two-nodes", "longest-cycle-in-a-graph"]}, {"contest_title": "\u7b2c 305 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 305", "contest_title_slug": "weekly-contest-305", "contest_id": 663, "contest_start_time": 1659839400, "contest_duration": 5400, "user_num": 7465, "question_slugs": ["number-of-arithmetic-triplets", "reachable-nodes-with-restrictions", "check-if-there-is-a-valid-partition-for-the-array", "longest-ideal-subsequence"]}, {"contest_title": "\u7b2c 306 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 306", "contest_title_slug": "weekly-contest-306", "contest_id": 669, "contest_start_time": 1660444200, "contest_duration": 5400, "user_num": 7500, "question_slugs": ["largest-local-values-in-a-matrix", "node-with-highest-edge-score", "construct-smallest-number-from-di-string", "count-special-integers"]}, {"contest_title": "\u7b2c 307 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 307", "contest_title_slug": "weekly-contest-307", "contest_id": 671, "contest_start_time": 1661049000, "contest_duration": 5400, "user_num": 7064, "question_slugs": ["minimum-hours-of-training-to-win-a-competition", "largest-palindromic-number", "amount-of-time-for-binary-tree-to-be-infected", "find-the-k-sum-of-an-array"]}, {"contest_title": "\u7b2c 308 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 308", "contest_title_slug": "weekly-contest-308", "contest_id": 689, "contest_start_time": 1661653800, "contest_duration": 5400, "user_num": 6394, "question_slugs": ["longest-subsequence-with-limited-sum", "removing-stars-from-a-string", "minimum-amount-of-time-to-collect-garbage", "build-a-matrix-with-conditions"]}, {"contest_title": "\u7b2c 309 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 309", "contest_title_slug": "weekly-contest-309", "contest_id": 693, "contest_start_time": 1662258600, "contest_duration": 5400, "user_num": 7972, "question_slugs": ["check-distances-between-same-letters", "number-of-ways-to-reach-a-position-after-exactly-k-steps", "longest-nice-subarray", "meeting-rooms-iii"]}, {"contest_title": "\u7b2c 310 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 310", "contest_title_slug": "weekly-contest-310", "contest_id": 704, "contest_start_time": 1662863400, "contest_duration": 5400, "user_num": 6081, "question_slugs": ["most-frequent-even-element", "optimal-partition-of-string", "divide-intervals-into-minimum-number-of-groups", "longest-increasing-subsequence-ii"]}, {"contest_title": "\u7b2c 311 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 311", "contest_title_slug": "weekly-contest-311", "contest_id": 741, "contest_start_time": 1663468200, "contest_duration": 5400, "user_num": 6710, "question_slugs": ["smallest-even-multiple", "length-of-the-longest-alphabetical-continuous-substring", "reverse-odd-levels-of-binary-tree", "sum-of-prefix-scores-of-strings"]}, {"contest_title": "\u7b2c 312 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 312", "contest_title_slug": "weekly-contest-312", "contest_id": 746, "contest_start_time": 1664073000, "contest_duration": 5400, "user_num": 6638, "question_slugs": ["sort-the-people", "longest-subarray-with-maximum-bitwise-and", "find-all-good-indices", "number-of-good-paths"]}, {"contest_title": "\u7b2c 313 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 313", "contest_title_slug": "weekly-contest-313", "contest_id": 750, "contest_start_time": 1664677800, "contest_duration": 5400, "user_num": 5445, "question_slugs": ["number-of-common-factors", "maximum-sum-of-an-hourglass", "minimize-xor", "maximum-deletions-on-a-string"]}, {"contest_title": "\u7b2c 314 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 314", "contest_title_slug": "weekly-contest-314", "contest_id": 756, "contest_start_time": 1665282600, "contest_duration": 5400, "user_num": 4838, "question_slugs": ["the-employee-that-worked-on-the-longest-task", "find-the-original-array-of-prefix-xor", "using-a-robot-to-print-the-lexicographically-smallest-string", "paths-in-matrix-whose-sum-is-divisible-by-k"]}, {"contest_title": "\u7b2c 315 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 315", "contest_title_slug": "weekly-contest-315", "contest_id": 759, "contest_start_time": 1665887400, "contest_duration": 5400, "user_num": 6490, "question_slugs": ["largest-positive-integer-that-exists-with-its-negative", "count-number-of-distinct-integers-after-reverse-operations", "sum-of-number-and-its-reverse", "count-subarrays-with-fixed-bounds"]}, {"contest_title": "\u7b2c 316 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 316", "contest_title_slug": "weekly-contest-316", "contest_id": 764, "contest_start_time": 1666492200, "contest_duration": 5400, "user_num": 6387, "question_slugs": ["determine-if-two-events-have-conflict", "number-of-subarrays-with-gcd-equal-to-k", "minimum-cost-to-make-array-equal", "minimum-number-of-operations-to-make-arrays-similar"]}, {"contest_title": "\u7b2c 317 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 317", "contest_title_slug": "weekly-contest-317", "contest_id": 767, "contest_start_time": 1667097000, "contest_duration": 5400, "user_num": 5660, "question_slugs": ["average-value-of-even-numbers-that-are-divisible-by-three", "most-popular-video-creator", "minimum-addition-to-make-integer-beautiful", "height-of-binary-tree-after-subtree-removal-queries"]}, {"contest_title": "\u7b2c 318 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 318", "contest_title_slug": "weekly-contest-318", "contest_id": 771, "contest_start_time": 1667701800, "contest_duration": 5400, "user_num": 5670, "question_slugs": ["apply-operations-to-an-array", "maximum-sum-of-distinct-subarrays-with-length-k", "total-cost-to-hire-k-workers", "minimum-total-distance-traveled"]}, {"contest_title": "\u7b2c 319 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 319", "contest_title_slug": "weekly-contest-319", "contest_id": 773, "contest_start_time": 1668306600, "contest_duration": 5400, "user_num": 6175, "question_slugs": ["convert-the-temperature", "number-of-subarrays-with-lcm-equal-to-k", "minimum-number-of-operations-to-sort-a-binary-tree-by-level", "maximum-number-of-non-overlapping-palindrome-substrings"]}, {"contest_title": "\u7b2c 320 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 320", "contest_title_slug": "weekly-contest-320", "contest_id": 777, "contest_start_time": 1668911400, "contest_duration": 5400, "user_num": 5678, "question_slugs": ["number-of-unequal-triplets-in-array", "closest-nodes-queries-in-a-binary-search-tree", "minimum-fuel-cost-to-report-to-the-capital", "number-of-beautiful-partitions"]}, {"contest_title": "\u7b2c 321 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 321", "contest_title_slug": "weekly-contest-321", "contest_id": 779, "contest_start_time": 1669516200, "contest_duration": 5400, "user_num": 5115, "question_slugs": ["find-the-pivot-integer", "append-characters-to-string-to-make-subsequence", "remove-nodes-from-linked-list", "count-subarrays-with-median-k"]}, {"contest_title": "\u7b2c 322 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 322", "contest_title_slug": "weekly-contest-322", "contest_id": 783, "contest_start_time": 1670121000, "contest_duration": 5400, "user_num": 5085, "question_slugs": ["circular-sentence", "divide-players-into-teams-of-equal-skill", "minimum-score-of-a-path-between-two-cities", "divide-nodes-into-the-maximum-number-of-groups"]}, {"contest_title": "\u7b2c 323 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 323", "contest_title_slug": "weekly-contest-323", "contest_id": 785, "contest_start_time": 1670725800, "contest_duration": 5400, "user_num": 4671, "question_slugs": ["delete-greatest-value-in-each-row", "longest-square-streak-in-an-array", "design-memory-allocator", "maximum-number-of-points-from-grid-queries"]}, {"contest_title": "\u7b2c 324 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 324", "contest_title_slug": "weekly-contest-324", "contest_id": 790, "contest_start_time": 1671330600, "contest_duration": 5400, "user_num": 4167, "question_slugs": ["count-pairs-of-similar-strings", "smallest-value-after-replacing-with-sum-of-prime-factors", "add-edges-to-make-degrees-of-all-nodes-even", "cycle-length-queries-in-a-tree"]}, {"contest_title": "\u7b2c 325 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 325", "contest_title_slug": "weekly-contest-325", "contest_id": 795, "contest_start_time": 1671935400, "contest_duration": 5400, "user_num": 3530, "question_slugs": ["shortest-distance-to-target-string-in-a-circular-array", "take-k-of-each-character-from-left-and-right", "maximum-tastiness-of-candy-basket", "number-of-great-partitions"]}, {"contest_title": "\u7b2c 326 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 326", "contest_title_slug": "weekly-contest-326", "contest_id": 799, "contest_start_time": 1672540200, "contest_duration": 5400, "user_num": 3873, "question_slugs": ["count-the-digits-that-divide-a-number", "distinct-prime-factors-of-product-of-array", "partition-string-into-substrings-with-values-at-most-k", "closest-prime-numbers-in-range"]}, {"contest_title": "\u7b2c 327 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 327", "contest_title_slug": "weekly-contest-327", "contest_id": 801, "contest_start_time": 1673145000, "contest_duration": 5400, "user_num": 4518, "question_slugs": ["maximum-count-of-positive-integer-and-negative-integer", "maximal-score-after-applying-k-operations", "make-number-of-distinct-characters-equal", "time-to-cross-a-bridge"]}, {"contest_title": "\u7b2c 328 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 328", "contest_title_slug": "weekly-contest-328", "contest_id": 805, "contest_start_time": 1673749800, "contest_duration": 5400, "user_num": 4776, "question_slugs": ["difference-between-element-sum-and-digit-sum-of-an-array", "increment-submatrices-by-one", "count-the-number-of-good-subarrays", "difference-between-maximum-and-minimum-price-sum"]}, {"contest_title": "\u7b2c 329 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 329", "contest_title_slug": "weekly-contest-329", "contest_id": 807, "contest_start_time": 1674354600, "contest_duration": 5400, "user_num": 2591, "question_slugs": ["alternating-digit-sum", "sort-the-students-by-their-kth-score", "apply-bitwise-operations-to-make-strings-equal", "minimum-cost-to-split-an-array"]}, {"contest_title": "\u7b2c 330 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 330", "contest_title_slug": "weekly-contest-330", "contest_id": 811, "contest_start_time": 1674959400, "contest_duration": 5400, "user_num": 3399, "question_slugs": ["count-distinct-numbers-on-board", "count-collisions-of-monkeys-on-a-polygon", "put-marbles-in-bags", "count-increasing-quadruplets"]}, {"contest_title": "\u7b2c 331 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 331", "contest_title_slug": "weekly-contest-331", "contest_id": 813, "contest_start_time": 1675564200, "contest_duration": 5400, "user_num": 4256, "question_slugs": ["take-gifts-from-the-richest-pile", "count-vowel-strings-in-ranges", "house-robber-iv", "rearranging-fruits"]}, {"contest_title": "\u7b2c 332 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 332", "contest_title_slug": "weekly-contest-332", "contest_id": 817, "contest_start_time": 1676169000, "contest_duration": 5400, "user_num": 4547, "question_slugs": ["find-the-array-concatenation-value", "count-the-number-of-fair-pairs", "substring-xor-queries", "subsequence-with-the-minimum-score"]}, {"contest_title": "\u7b2c 333 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 333", "contest_title_slug": "weekly-contest-333", "contest_id": 819, "contest_start_time": 1676773800, "contest_duration": 5400, "user_num": 4969, "question_slugs": ["merge-two-2d-arrays-by-summing-values", "minimum-operations-to-reduce-an-integer-to-0", "count-the-number-of-square-free-subsets", "find-the-string-with-lcp"]}, {"contest_title": "\u7b2c 334 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 334", "contest_title_slug": "weekly-contest-334", "contest_id": 823, "contest_start_time": 1677378600, "contest_duration": 5400, "user_num": 5501, "question_slugs": ["left-and-right-sum-differences", "find-the-divisibility-array-of-a-string", "find-the-maximum-number-of-marked-indices", "minimum-time-to-visit-a-cell-in-a-grid"]}, {"contest_title": "\u7b2c 335 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 335", "contest_title_slug": "weekly-contest-335", "contest_id": 825, "contest_start_time": 1677983400, "contest_duration": 5400, "user_num": 6019, "question_slugs": ["pass-the-pillow", "kth-largest-sum-in-a-binary-tree", "split-the-array-to-make-coprime-products", "number-of-ways-to-earn-points"]}, {"contest_title": "\u7b2c 336 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 336", "contest_title_slug": "weekly-contest-336", "contest_id": 833, "contest_start_time": 1678588200, "contest_duration": 5400, "user_num": 5897, "question_slugs": ["count-the-number-of-vowel-strings-in-range", "rearrange-array-to-maximize-prefix-score", "count-the-number-of-beautiful-subarrays", "minimum-time-to-complete-all-tasks"]}, {"contest_title": "\u7b2c 337 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 337", "contest_title_slug": "weekly-contest-337", "contest_id": 839, "contest_start_time": 1679193000, "contest_duration": 5400, "user_num": 5628, "question_slugs": ["number-of-even-and-odd-bits", "check-knight-tour-configuration", "the-number-of-beautiful-subsets", "smallest-missing-non-negative-integer-after-operations"]}, {"contest_title": "\u7b2c 338 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 338", "contest_title_slug": "weekly-contest-338", "contest_id": 843, "contest_start_time": 1679797800, "contest_duration": 5400, "user_num": 5594, "question_slugs": ["k-items-with-the-maximum-sum", "prime-subtraction-operation", "minimum-operations-to-make-all-array-elements-equal", "collect-coins-in-a-tree"]}, {"contest_title": "\u7b2c 339 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 339", "contest_title_slug": "weekly-contest-339", "contest_id": 850, "contest_start_time": 1680402600, "contest_duration": 5400, "user_num": 5180, "question_slugs": ["find-the-longest-balanced-substring-of-a-binary-string", "convert-an-array-into-a-2d-array-with-conditions", "mice-and-cheese", "minimum-reverse-operations"]}, {"contest_title": "\u7b2c 340 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 340", "contest_title_slug": "weekly-contest-340", "contest_id": 854, "contest_start_time": 1681007400, "contest_duration": 5400, "user_num": 4937, "question_slugs": ["prime-in-diagonal", "sum-of-distances", "minimize-the-maximum-difference-of-pairs", "minimum-number-of-visited-cells-in-a-grid"]}, {"contest_title": "\u7b2c 341 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 341", "contest_title_slug": "weekly-contest-341", "contest_id": 856, "contest_start_time": 1681612200, "contest_duration": 5400, "user_num": 4792, "question_slugs": ["row-with-maximum-ones", "find-the-maximum-divisibility-score", "minimum-additions-to-make-valid-string", "minimize-the-total-price-of-the-trips"]}, {"contest_title": "\u7b2c 342 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 342", "contest_title_slug": "weekly-contest-342", "contest_id": 860, "contest_start_time": 1682217000, "contest_duration": 5400, "user_num": 3702, "question_slugs": ["calculate-delayed-arrival-time", "sum-multiples", "sliding-subarray-beauty", "minimum-number-of-operations-to-make-all-array-elements-equal-to-1"]}, {"contest_title": "\u7b2c 343 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 343", "contest_title_slug": "weekly-contest-343", "contest_id": 863, "contest_start_time": 1682821800, "contest_duration": 5400, "user_num": 3313, "question_slugs": ["determine-the-winner-of-a-bowling-game", "first-completely-painted-row-or-column", "minimum-cost-of-a-path-with-special-roads", "lexicographically-smallest-beautiful-string"]}, {"contest_title": "\u7b2c 344 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 344", "contest_title_slug": "weekly-contest-344", "contest_id": 867, "contest_start_time": 1683426600, "contest_duration": 5400, "user_num": 3986, "question_slugs": ["find-the-distinct-difference-array", "frequency-tracker", "number-of-adjacent-elements-with-the-same-color", "make-costs-of-paths-equal-in-a-binary-tree"]}, {"contest_title": "\u7b2c 345 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 345", "contest_title_slug": "weekly-contest-345", "contest_id": 870, "contest_start_time": 1684031400, "contest_duration": 5400, "user_num": 4165, "question_slugs": ["find-the-losers-of-the-circular-game", "neighboring-bitwise-xor", "maximum-number-of-moves-in-a-grid", "count-the-number-of-complete-components"]}, {"contest_title": "\u7b2c 346 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 346", "contest_title_slug": "weekly-contest-346", "contest_id": 874, "contest_start_time": 1684636200, "contest_duration": 5400, "user_num": 4035, "question_slugs": ["minimum-string-length-after-removing-substrings", "lexicographically-smallest-palindrome", "find-the-punishment-number-of-an-integer", "modify-graph-edge-weights"]}, {"contest_title": "\u7b2c 347 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 347", "contest_title_slug": "weekly-contest-347", "contest_id": 876, "contest_start_time": 1685241000, "contest_duration": 5400, "user_num": 3836, "question_slugs": ["remove-trailing-zeros-from-a-string", "difference-of-number-of-distinct-values-on-diagonals", "minimum-cost-to-make-all-characters-equal", "maximum-strictly-increasing-cells-in-a-matrix"]}, {"contest_title": "\u7b2c 348 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 348", "contest_title_slug": "weekly-contest-348", "contest_id": 880, "contest_start_time": 1685845800, "contest_duration": 5400, "user_num": 3909, "question_slugs": ["minimize-string-length", "semi-ordered-permutation", "sum-of-matrix-after-queries", "count-of-integers"]}, {"contest_title": "\u7b2c 349 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 349", "contest_title_slug": "weekly-contest-349", "contest_id": 882, "contest_start_time": 1686450600, "contest_duration": 5400, "user_num": 3714, "question_slugs": ["neither-minimum-nor-maximum", "lexicographically-smallest-string-after-substring-operation", "collecting-chocolates", "maximum-sum-queries"]}, {"contest_title": "\u7b2c 350 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 350", "contest_title_slug": "weekly-contest-350", "contest_id": 886, "contest_start_time": 1687055400, "contest_duration": 5400, "user_num": 3580, "question_slugs": ["total-distance-traveled", "find-the-value-of-the-partition", "special-permutations", "painting-the-walls"]}, {"contest_title": "\u7b2c 351 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 351", "contest_title_slug": "weekly-contest-351", "contest_id": 888, "contest_start_time": 1687660200, "contest_duration": 5400, "user_num": 2471, "question_slugs": ["number-of-beautiful-pairs", "minimum-operations-to-make-the-integer-zero", "ways-to-split-array-into-good-subarrays", "robot-collisions"]}, {"contest_title": "\u7b2c 352 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 352", "contest_title_slug": "weekly-contest-352", "contest_id": 892, "contest_start_time": 1688265000, "contest_duration": 5400, "user_num": 3437, "question_slugs": ["longest-even-odd-subarray-with-threshold", "prime-pairs-with-target-sum", "continuous-subarrays", "sum-of-imbalance-numbers-of-all-subarrays"]}, {"contest_title": "\u7b2c 353 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 353", "contest_title_slug": "weekly-contest-353", "contest_id": 894, "contest_start_time": 1688869800, "contest_duration": 5400, "user_num": 4113, "question_slugs": ["find-the-maximum-achievable-number", "maximum-number-of-jumps-to-reach-the-last-index", "longest-non-decreasing-subarray-from-two-arrays", "apply-operations-to-make-all-array-elements-equal-to-zero"]}, {"contest_title": "\u7b2c 354 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 354", "contest_title_slug": "weekly-contest-354", "contest_id": 898, "contest_start_time": 1689474600, "contest_duration": 5400, "user_num": 3957, "question_slugs": ["sum-of-squares-of-special-elements", "maximum-beauty-of-an-array-after-applying-operation", "minimum-index-of-a-valid-split", "length-of-the-longest-valid-substring"]}, {"contest_title": "\u7b2c 355 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 355", "contest_title_slug": "weekly-contest-355", "contest_id": 900, "contest_start_time": 1690079400, "contest_duration": 5400, "user_num": 4112, "question_slugs": ["split-strings-by-separator", "largest-element-in-an-array-after-merge-operations", "maximum-number-of-groups-with-increasing-length", "count-paths-that-can-form-a-palindrome-in-a-tree"]}, {"contest_title": "\u7b2c 356 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 356", "contest_title_slug": "weekly-contest-356", "contest_id": 904, "contest_start_time": 1690684200, "contest_duration": 5400, "user_num": 4082, "question_slugs": ["number-of-employees-who-met-the-target", "count-complete-subarrays-in-an-array", "shortest-string-that-contains-three-strings", "count-stepping-numbers-in-range"]}, {"contest_title": "\u7b2c 357 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 357", "contest_title_slug": "weekly-contest-357", "contest_id": 906, "contest_start_time": 1691289000, "contest_duration": 5400, "user_num": 4265, "question_slugs": ["faulty-keyboard", "check-if-it-is-possible-to-split-array", "find-the-safest-path-in-a-grid", "maximum-elegance-of-a-k-length-subsequence"]}, {"contest_title": "\u7b2c 358 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 358", "contest_title_slug": "weekly-contest-358", "contest_id": 910, "contest_start_time": 1691893800, "contest_duration": 5400, "user_num": 4475, "question_slugs": ["max-pair-sum-in-an-array", "double-a-number-represented-as-a-linked-list", "minimum-absolute-difference-between-elements-with-constraint", "apply-operations-to-maximize-score"]}, {"contest_title": "\u7b2c 359 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 359", "contest_title_slug": "weekly-contest-359", "contest_id": 913, "contest_start_time": 1692498600, "contest_duration": 5400, "user_num": 4101, "question_slugs": ["check-if-a-string-is-an-acronym-of-words", "determine-the-minimum-sum-of-a-k-avoiding-array", "maximize-the-profit-as-the-salesman", "find-the-longest-equal-subarray"]}, {"contest_title": "\u7b2c 360 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 360", "contest_title_slug": "weekly-contest-360", "contest_id": 918, "contest_start_time": 1693103400, "contest_duration": 5400, "user_num": 4496, "question_slugs": ["furthest-point-from-origin", "find-the-minimum-possible-sum-of-a-beautiful-array", "minimum-operations-to-form-subsequence-with-target-sum", "maximize-value-of-function-in-a-ball-passing-game"]}, {"contest_title": "\u7b2c 361 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 361", "contest_title_slug": "weekly-contest-361", "contest_id": 920, "contest_start_time": 1693708200, "contest_duration": 5400, "user_num": 4170, "question_slugs": ["count-symmetric-integers", "minimum-operations-to-make-a-special-number", "count-of-interesting-subarrays", "minimum-edge-weight-equilibrium-queries-in-a-tree"]}, {"contest_title": "\u7b2c 362 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 362", "contest_title_slug": "weekly-contest-362", "contest_id": 924, "contest_start_time": 1694313000, "contest_duration": 5400, "user_num": 4800, "question_slugs": ["points-that-intersect-with-cars", "determine-if-a-cell-is-reachable-at-a-given-time", "minimum-moves-to-spread-stones-over-grid", "string-transformation"]}, {"contest_title": "\u7b2c 363 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 363", "contest_title_slug": "weekly-contest-363", "contest_id": 926, "contest_start_time": 1694917800, "contest_duration": 5400, "user_num": 4768, "question_slugs": ["sum-of-values-at-indices-with-k-set-bits", "happy-students", "maximum-number-of-alloys", "maximum-element-sum-of-a-complete-subset-of-indices"]}, {"contest_title": "\u7b2c 364 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 364", "contest_title_slug": "weekly-contest-364", "contest_id": 930, "contest_start_time": 1695522600, "contest_duration": 5400, "user_num": 4304, "question_slugs": ["maximum-odd-binary-number", "beautiful-towers-i", "beautiful-towers-ii", "count-valid-paths-in-a-tree"]}, {"contest_title": "\u7b2c 365 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 365", "contest_title_slug": "weekly-contest-365", "contest_id": 932, "contest_start_time": 1696127400, "contest_duration": 5400, "user_num": 2909, "question_slugs": ["maximum-value-of-an-ordered-triplet-i", "maximum-value-of-an-ordered-triplet-ii", "minimum-size-subarray-in-infinite-array", "count-visited-nodes-in-a-directed-graph"]}, {"contest_title": "\u7b2c 366 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 366", "contest_title_slug": "weekly-contest-366", "contest_id": 936, "contest_start_time": 1696732200, "contest_duration": 5400, "user_num": 2790, "question_slugs": ["divisible-and-non-divisible-sums-difference", "minimum-processing-time", "apply-operations-to-make-two-strings-equal", "apply-operations-on-array-to-maximize-sum-of-squares"]}, {"contest_title": "\u7b2c 367 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 367", "contest_title_slug": "weekly-contest-367", "contest_id": 938, "contest_start_time": 1697337000, "contest_duration": 5400, "user_num": 4317, "question_slugs": ["find-indices-with-index-and-value-difference-i", "shortest-and-lexicographically-smallest-beautiful-string", "find-indices-with-index-and-value-difference-ii", "construct-product-matrix"]}, {"contest_title": "\u7b2c 368 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 368", "contest_title_slug": "weekly-contest-368", "contest_id": 942, "contest_start_time": 1697941800, "contest_duration": 5400, "user_num": 5002, "question_slugs": ["minimum-sum-of-mountain-triplets-i", "minimum-sum-of-mountain-triplets-ii", "minimum-number-of-groups-to-create-a-valid-assignment", "minimum-changes-to-make-k-semi-palindromes"]}, {"contest_title": "\u7b2c 369 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 369", "contest_title_slug": "weekly-contest-369", "contest_id": 945, "contest_start_time": 1698546600, "contest_duration": 5400, "user_num": 4121, "question_slugs": ["find-the-k-or-of-an-array", "minimum-equal-sum-of-two-arrays-after-replacing-zeros", "minimum-increment-operations-to-make-array-beautiful", "maximum-points-after-collecting-coins-from-all-nodes"]}, {"contest_title": "\u7b2c 370 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 370", "contest_title_slug": "weekly-contest-370", "contest_id": 950, "contest_start_time": 1699151400, "contest_duration": 5400, "user_num": 3983, "question_slugs": ["find-champion-i", "find-champion-ii", "maximum-score-after-applying-operations-on-a-tree", "maximum-balanced-subsequence-sum"]}, {"contest_title": "\u7b2c 371 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 371", "contest_title_slug": "weekly-contest-371", "contest_id": 952, "contest_start_time": 1699756200, "contest_duration": 5400, "user_num": 3638, "question_slugs": ["maximum-strong-pair-xor-i", "high-access-employees", "minimum-operations-to-maximize-last-elements-in-arrays", "maximum-strong-pair-xor-ii"]}, {"contest_title": "\u7b2c 372 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 372", "contest_title_slug": "weekly-contest-372", "contest_id": 956, "contest_start_time": 1700361000, "contest_duration": 5400, "user_num": 3920, "question_slugs": ["make-three-strings-equal", "separate-black-and-white-balls", "maximum-xor-product", "find-building-where-alice-and-bob-can-meet"]}, {"contest_title": "\u7b2c 373 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 373", "contest_title_slug": "weekly-contest-373", "contest_id": 958, "contest_start_time": 1700965800, "contest_duration": 5400, "user_num": 3577, "question_slugs": ["matrix-similarity-after-cyclic-shifts", "count-beautiful-substrings-i", "make-lexicographically-smallest-array-by-swapping-elements", "count-beautiful-substrings-ii"]}, {"contest_title": "\u7b2c 374 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 374", "contest_title_slug": "weekly-contest-374", "contest_id": 962, "contest_start_time": 1701570600, "contest_duration": 5400, "user_num": 4053, "question_slugs": ["find-the-peaks", "minimum-number-of-coins-to-be-added", "count-complete-substrings", "count-the-number-of-infection-sequences"]}, {"contest_title": "\u7b2c 375 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 375", "contest_title_slug": "weekly-contest-375", "contest_id": 964, "contest_start_time": 1702175400, "contest_duration": 5400, "user_num": 3518, "question_slugs": ["count-tested-devices-after-test-operations", "double-modular-exponentiation", "count-subarrays-where-max-element-appears-at-least-k-times", "count-the-number-of-good-partitions"]}, {"contest_title": "\u7b2c 376 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 376", "contest_title_slug": "weekly-contest-376", "contest_id": 968, "contest_start_time": 1702780200, "contest_duration": 5400, "user_num": 3409, "question_slugs": ["find-missing-and-repeated-values", "divide-array-into-arrays-with-max-difference", "minimum-cost-to-make-array-equalindromic", "apply-operations-to-maximize-frequency-score"]}, {"contest_title": "\u7b2c 377 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 377", "contest_title_slug": "weekly-contest-377", "contest_id": 970, "contest_start_time": 1703385000, "contest_duration": 5400, "user_num": 3148, "question_slugs": ["minimum-number-game", "maximum-square-area-by-removing-fences-from-a-field", "minimum-cost-to-convert-string-i", "minimum-cost-to-convert-string-ii"]}, {"contest_title": "\u7b2c 378 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 378", "contest_title_slug": "weekly-contest-378", "contest_id": 974, "contest_start_time": 1703989800, "contest_duration": 5400, "user_num": 2747, "question_slugs": ["check-if-bitwise-or-has-trailing-zeros", "find-longest-special-substring-that-occurs-thrice-i", "find-longest-special-substring-that-occurs-thrice-ii", "palindrome-rearrangement-queries"]}, {"contest_title": "\u7b2c 379 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 379", "contest_title_slug": "weekly-contest-379", "contest_id": 976, "contest_start_time": 1704594600, "contest_duration": 5400, "user_num": 3117, "question_slugs": ["maximum-area-of-longest-diagonal-rectangle", "minimum-moves-to-capture-the-queen", "maximum-size-of-a-set-after-removals", "maximize-the-number-of-partitions-after-operations"]}, {"contest_title": "\u7b2c 380 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 380", "contest_title_slug": "weekly-contest-380", "contest_id": 980, "contest_start_time": 1705199400, "contest_duration": 5400, "user_num": 3325, "question_slugs": ["count-elements-with-maximum-frequency", "find-beautiful-indices-in-the-given-array-i", "maximum-number-that-sum-of-the-prices-is-less-than-or-equal-to-k", "find-beautiful-indices-in-the-given-array-ii"]}, {"contest_title": "\u7b2c 381 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 381", "contest_title_slug": "weekly-contest-381", "contest_id": 982, "contest_start_time": 1705804200, "contest_duration": 5400, "user_num": 3737, "question_slugs": ["minimum-number-of-pushes-to-type-word-i", "count-the-number-of-houses-at-a-certain-distance-i", "minimum-number-of-pushes-to-type-word-ii", "count-the-number-of-houses-at-a-certain-distance-ii"]}, {"contest_title": "\u7b2c 382 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 382", "contest_title_slug": "weekly-contest-382", "contest_id": 986, "contest_start_time": 1706409000, "contest_duration": 5400, "user_num": 3134, "question_slugs": ["number-of-changing-keys", "find-the-maximum-number-of-elements-in-subset", "alice-and-bob-playing-flower-game", "minimize-or-of-remaining-elements-using-operations"]}, {"contest_title": "\u7b2c 383 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 383", "contest_title_slug": "weekly-contest-383", "contest_id": 988, "contest_start_time": 1707013800, "contest_duration": 5400, "user_num": 2691, "question_slugs": ["ant-on-the-boundary", "minimum-time-to-revert-word-to-initial-state-i", "find-the-grid-of-region-average", "minimum-time-to-revert-word-to-initial-state-ii"]}, {"contest_title": "\u7b2c 384 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 384", "contest_title_slug": "weekly-contest-384", "contest_id": 992, "contest_start_time": 1707618600, "contest_duration": 5400, "user_num": 1652, "question_slugs": ["modify-the-matrix", "number-of-subarrays-that-match-a-pattern-i", "maximum-palindromes-after-operations", "number-of-subarrays-that-match-a-pattern-ii"]}, {"contest_title": "\u7b2c 385 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 385", "contest_title_slug": "weekly-contest-385", "contest_id": 994, "contest_start_time": 1708223400, "contest_duration": 5400, "user_num": 2382, "question_slugs": ["count-prefix-and-suffix-pairs-i", "find-the-length-of-the-longest-common-prefix", "most-frequent-prime", "count-prefix-and-suffix-pairs-ii"]}, {"contest_title": "\u7b2c 386 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 386", "contest_title_slug": "weekly-contest-386", "contest_id": 998, "contest_start_time": 1708828200, "contest_duration": 5400, "user_num": 2731, "question_slugs": ["split-the-array", "find-the-largest-area-of-square-inside-two-rectangles", "earliest-second-to-mark-indices-i", "earliest-second-to-mark-indices-ii"]}, {"contest_title": "\u7b2c 387 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 387", "contest_title_slug": "weekly-contest-387", "contest_id": 1000, "contest_start_time": 1709433000, "contest_duration": 5400, "user_num": 3694, "question_slugs": ["distribute-elements-into-two-arrays-i", "count-submatrices-with-top-left-element-and-sum-less-than-k", "minimum-operations-to-write-the-letter-y-on-a-grid", "distribute-elements-into-two-arrays-ii"]}, {"contest_title": "\u7b2c 388 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 388", "contest_title_slug": "weekly-contest-388", "contest_id": 1004, "contest_start_time": 1710037800, "contest_duration": 5400, "user_num": 4291, "question_slugs": ["apple-redistribution-into-boxes", "maximize-happiness-of-selected-children", "shortest-uncommon-substring-in-an-array", "maximum-strength-of-k-disjoint-subarrays"]}, {"contest_title": "\u7b2c 389 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 389", "contest_title_slug": "weekly-contest-389", "contest_id": 1006, "contest_start_time": 1710642600, "contest_duration": 5400, "user_num": 4561, "question_slugs": ["existence-of-a-substring-in-a-string-and-its-reverse", "count-substrings-starting-and-ending-with-given-character", "minimum-deletions-to-make-string-k-special", "minimum-moves-to-pick-k-ones"]}, {"contest_title": "\u7b2c 390 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 390", "contest_title_slug": "weekly-contest-390", "contest_id": 1011, "contest_start_time": 1711247400, "contest_duration": 5400, "user_num": 4817, "question_slugs": ["maximum-length-substring-with-two-occurrences", "apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k", "most-frequent-ids", "longest-common-suffix-queries"]}, {"contest_title": "\u7b2c 391 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 391", "contest_title_slug": "weekly-contest-391", "contest_id": 1014, "contest_start_time": 1711852200, "contest_duration": 5400, "user_num": 4181, "question_slugs": ["harshad-number", "water-bottles-ii", "count-alternating-subarrays", "minimize-manhattan-distances"]}, {"contest_title": "\u7b2c 392 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 392", "contest_title_slug": "weekly-contest-392", "contest_id": 1018, "contest_start_time": 1712457000, "contest_duration": 5400, "user_num": 3194, "question_slugs": ["longest-strictly-increasing-or-strictly-decreasing-subarray", "lexicographically-smallest-string-after-operations-with-constraint", "minimum-operations-to-make-median-of-array-equal-to-k", "minimum-cost-walk-in-weighted-graph"]}, {"contest_title": "\u7b2c 393 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 393", "contest_title_slug": "weekly-contest-393", "contest_id": 1020, "contest_start_time": 1713061800, "contest_duration": 5400, "user_num": 4219, "question_slugs": ["latest-time-you-can-obtain-after-replacing-characters", "maximum-prime-difference", "kth-smallest-amount-with-single-denomination-combination", "minimum-sum-of-values-by-dividing-array"]}, {"contest_title": "\u7b2c 394 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 394", "contest_title_slug": "weekly-contest-394", "contest_id": 1024, "contest_start_time": 1713666600, "contest_duration": 5400, "user_num": 3958, "question_slugs": ["count-the-number-of-special-characters-i", "count-the-number-of-special-characters-ii", "minimum-number-of-operations-to-satisfy-conditions", "find-edges-in-shortest-paths"]}, {"contest_title": "\u7b2c 395 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 395", "contest_title_slug": "weekly-contest-395", "contest_id": 1026, "contest_start_time": 1714271400, "contest_duration": 5400, "user_num": 2969, "question_slugs": ["find-the-integer-added-to-array-i", "find-the-integer-added-to-array-ii", "minimum-array-end", "find-the-median-of-the-uniqueness-array"]}, {"contest_title": "\u7b2c 396 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 396", "contest_title_slug": "weekly-contest-396", "contest_id": 1030, "contest_start_time": 1714876200, "contest_duration": 5400, "user_num": 2932, "question_slugs": ["valid-word", "minimum-number-of-operations-to-make-word-k-periodic", "minimum-length-of-anagram-concatenation", "minimum-cost-to-equalize-array"]}, {"contest_title": "\u7b2c 397 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 397", "contest_title_slug": "weekly-contest-397", "contest_id": 1032, "contest_start_time": 1715481000, "contest_duration": 5400, "user_num": 3365, "question_slugs": ["permutation-difference-between-two-strings", "taking-maximum-energy-from-the-mystic-dungeon", "maximum-difference-score-in-a-grid", "find-the-minimum-cost-array-permutation"]}, {"contest_title": "\u7b2c 398 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 398", "contest_title_slug": "weekly-contest-398", "contest_id": 1036, "contest_start_time": 1716085800, "contest_duration": 5400, "user_num": 3606, "question_slugs": ["special-array-i", "special-array-ii", "sum-of-digit-differences-of-all-pairs", "find-number-of-ways-to-reach-the-k-th-stair"]}, {"contest_title": "\u7b2c 399 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 399", "contest_title_slug": "weekly-contest-399", "contest_id": 1038, "contest_start_time": 1716690600, "contest_duration": 5400, "user_num": 3424, "question_slugs": ["find-the-number-of-good-pairs-i", "string-compression-iii", "find-the-number-of-good-pairs-ii", "maximum-sum-of-subsequence-with-non-adjacent-elements"]}, {"contest_title": "\u7b2c 400 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 400", "contest_title_slug": "weekly-contest-400", "contest_id": 1043, "contest_start_time": 1717295400, "contest_duration": 5400, "user_num": 3534, "question_slugs": ["minimum-number-of-chairs-in-a-waiting-room", "count-days-without-meetings", "lexicographically-minimum-string-after-removing-stars", "find-subarray-with-bitwise-or-closest-to-k"]}, {"contest_title": "\u7b2c 401 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 401", "contest_title_slug": "weekly-contest-401", "contest_id": 1045, "contest_start_time": 1717900200, "contest_duration": 5400, "user_num": 3160, "question_slugs": ["find-the-child-who-has-the-ball-after-k-seconds", "find-the-n-th-value-after-k-seconds", "maximum-total-reward-using-operations-i", "maximum-total-reward-using-operations-ii"]}, {"contest_title": "\u7b2c 402 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 402", "contest_title_slug": "weekly-contest-402", "contest_id": 1049, "contest_start_time": 1718505000, "contest_duration": 5400, "user_num": 3283, "question_slugs": ["count-pairs-that-form-a-complete-day-i", "count-pairs-that-form-a-complete-day-ii", "maximum-total-damage-with-spell-casting", "peaks-in-array"]}, {"contest_title": "\u7b2c 403 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 403", "contest_title_slug": "weekly-contest-403", "contest_id": 1052, "contest_start_time": 1719109800, "contest_duration": 5400, "user_num": 3112, "question_slugs": ["minimum-average-of-smallest-and-largest-elements", "find-the-minimum-area-to-cover-all-ones-i", "maximize-total-cost-of-alternating-subarrays", "find-the-minimum-area-to-cover-all-ones-ii"]}, {"contest_title": "\u7b2c 404 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 404", "contest_title_slug": "weekly-contest-404", "contest_id": 1056, "contest_start_time": 1719714600, "contest_duration": 5400, "user_num": 3486, "question_slugs": ["maximum-height-of-a-triangle", "find-the-maximum-length-of-valid-subsequence-i", "find-the-maximum-length-of-valid-subsequence-ii", "find-minimum-diameter-after-merging-two-trees"]}, {"contest_title": "\u7b2c 405 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 405", "contest_title_slug": "weekly-contest-405", "contest_id": 1058, "contest_start_time": 1720319400, "contest_duration": 5400, "user_num": 3240, "question_slugs": ["find-the-encrypted-string", "generate-binary-strings-without-adjacent-zeros", "count-submatrices-with-equal-frequency-of-x-and-y", "construct-string-with-minimum-cost"]}, {"contest_title": "\u7b2c 406 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 406", "contest_title_slug": "weekly-contest-406", "contest_id": 1062, "contest_start_time": 1720924200, "contest_duration": 5400, "user_num": 3422, "question_slugs": ["lexicographically-smallest-string-after-a-swap", "delete-nodes-from-linked-list-present-in-array", "minimum-cost-for-cutting-cake-i", "minimum-cost-for-cutting-cake-ii"]}, {"contest_title": "\u7b2c 407 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 407", "contest_title_slug": "weekly-contest-407", "contest_id": 1064, "contest_start_time": 1721529000, "contest_duration": 5400, "user_num": 3268, "question_slugs": ["number-of-bit-changes-to-make-two-integers-equal", "vowels-game-in-a-string", "maximum-number-of-operations-to-move-ones-to-the-end", "minimum-operations-to-make-array-equal-to-target"]}, {"contest_title": "\u7b2c 408 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 408", "contest_title_slug": "weekly-contest-408", "contest_id": 1069, "contest_start_time": 1722133800, "contest_duration": 5400, "user_num": 3369, "question_slugs": ["find-if-digit-game-can-be-won", "find-the-count-of-numbers-which-are-not-special", "count-the-number-of-substrings-with-dominant-ones", "check-if-the-rectangle-corner-is-reachable"]}, {"contest_title": "\u7b2c 409 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 409", "contest_title_slug": "weekly-contest-409", "contest_id": 1071, "contest_start_time": 1722738600, "contest_duration": 5400, "user_num": 3643, "question_slugs": ["design-neighbor-sum-service", "shortest-distance-after-road-addition-queries-i", "shortest-distance-after-road-addition-queries-ii", "alternating-groups-iii"]}, {"contest_title": "\u7b2c 1 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 1", "contest_title_slug": "biweekly-contest-1", "contest_id": 70, "contest_start_time": 1559399400, "contest_duration": 7200, "user_num": 197, "question_slugs": ["fixed-point", "index-pairs-of-a-string", "campus-bikes-ii", "digit-count-in-range"]}, {"contest_title": "\u7b2c 2 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 2", "contest_title_slug": "biweekly-contest-2", "contest_id": 73, "contest_start_time": 1560609000, "contest_duration": 5400, "user_num": 256, "question_slugs": ["sum-of-digits-in-the-minimum-number", "high-five", "brace-expansion", "confusing-number-ii"]}, {"contest_title": "\u7b2c 3 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 3", "contest_title_slug": "biweekly-contest-3", "contest_id": 85, "contest_start_time": 1561818600, "contest_duration": 5400, "user_num": 312, "question_slugs": ["two-sum-less-than-k", "find-k-length-substrings-with-no-repeated-characters", "the-earliest-moment-when-everyone-become-friends", "path-with-maximum-minimum-value"]}, {"contest_title": "\u7b2c 4 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 4", "contest_title_slug": "biweekly-contest-4", "contest_id": 88, "contest_start_time": 1563028200, "contest_duration": 5400, "user_num": 438, "question_slugs": ["number-of-days-in-a-month", "remove-vowels-from-a-string", "maximum-average-subtree", "divide-array-into-increasing-sequences"]}, {"contest_title": "\u7b2c 5 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 5", "contest_title_slug": "biweekly-contest-5", "contest_id": 91, "contest_start_time": 1564237800, "contest_duration": 5400, "user_num": 495, "question_slugs": ["largest-unique-number", "armstrong-number", "connecting-cities-with-minimum-cost", "parallel-courses"]}, {"contest_title": "\u7b2c 6 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 6", "contest_title_slug": "biweekly-contest-6", "contest_id": 95, "contest_start_time": 1565447400, "contest_duration": 5400, "user_num": 513, "question_slugs": ["check-if-a-number-is-majority-element-in-a-sorted-array", "minimum-swaps-to-group-all-1s-together", "analyze-user-website-visit-pattern", "string-transforms-into-another-string"]}, {"contest_title": "\u7b2c 7 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 7", "contest_title_slug": "biweekly-contest-7", "contest_id": 99, "contest_start_time": 1566657000, "contest_duration": 5400, "user_num": 561, "question_slugs": ["single-row-keyboard", "design-file-system", "minimum-cost-to-connect-sticks", "optimize-water-distribution-in-a-village"]}, {"contest_title": "\u7b2c 8 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 8", "contest_title_slug": "biweekly-contest-8", "contest_id": 103, "contest_start_time": 1567866600, "contest_duration": 5400, "user_num": 630, "question_slugs": ["count-substrings-with-only-one-distinct-letter", "before-and-after-puzzle", "shortest-distance-to-target-color", "maximum-number-of-ones"]}, {"contest_title": "\u7b2c 9 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 9", "contest_title_slug": "biweekly-contest-9", "contest_id": 108, "contest_start_time": 1569076200, "contest_duration": 5700, "user_num": 929, "question_slugs": ["how-many-apples-can-you-put-into-the-basket", "minimum-knight-moves", "find-smallest-common-element-in-all-rows", "minimum-time-to-build-blocks"]}, {"contest_title": "\u7b2c 10 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 10", "contest_title_slug": "biweekly-contest-10", "contest_id": 115, "contest_start_time": 1570285800, "contest_duration": 5400, "user_num": 738, "question_slugs": ["intersection-of-three-sorted-arrays", "two-sum-bsts", "stepping-numbers", "valid-palindrome-iii"]}, {"contest_title": "\u7b2c 11 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 11", "contest_title_slug": "biweekly-contest-11", "contest_id": 118, "contest_start_time": 1571495400, "contest_duration": 5400, "user_num": 913, "question_slugs": ["missing-number-in-arithmetic-progression", "meeting-scheduler", "toss-strange-coins", "divide-chocolate"]}, {"contest_title": "\u7b2c 12 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 12", "contest_title_slug": "biweekly-contest-12", "contest_id": 121, "contest_start_time": 1572705000, "contest_duration": 5400, "user_num": 911, "question_slugs": ["design-a-leaderboard", "array-transformation", "tree-diameter", "palindrome-removal"]}, {"contest_title": "\u7b2c 13 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 13", "contest_title_slug": "biweekly-contest-13", "contest_id": 124, "contest_start_time": 1573914600, "contest_duration": 5400, "user_num": 810, "question_slugs": ["encode-number", "smallest-common-region", "synonymous-sentences", "handshakes-that-dont-cross"]}, {"contest_title": "\u7b2c 14 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 14", "contest_title_slug": "biweekly-contest-14", "contest_id": 129, "contest_start_time": 1575124200, "contest_duration": 5400, "user_num": 871, "question_slugs": ["hexspeak", "remove-interval", "delete-tree-nodes", "number-of-ships-in-a-rectangle"]}, {"contest_title": "\u7b2c 15 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 15", "contest_title_slug": "biweekly-contest-15", "contest_id": 132, "contest_start_time": 1576333800, "contest_duration": 5400, "user_num": 797, "question_slugs": ["element-appearing-more-than-25-in-sorted-array", "remove-covered-intervals", "iterator-for-combination", "minimum-falling-path-sum-ii"]}, {"contest_title": "\u7b2c 16 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 16", "contest_title_slug": "biweekly-contest-16", "contest_id": 135, "contest_start_time": 1577543400, "contest_duration": 5400, "user_num": 822, "question_slugs": ["replace-elements-with-greatest-element-on-right-side", "sum-of-mutated-array-closest-to-target", "deepest-leaves-sum", "number-of-paths-with-max-score"]}, {"contest_title": "\u7b2c 17 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 17", "contest_title_slug": "biweekly-contest-17", "contest_id": 138, "contest_start_time": 1578753000, "contest_duration": 5400, "user_num": 897, "question_slugs": ["decompress-run-length-encoded-list", "matrix-block-sum", "sum-of-nodes-with-even-valued-grandparent", "distinct-echo-substrings"]}, {"contest_title": "\u7b2c 18 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 18", "contest_title_slug": "biweekly-contest-18", "contest_id": 143, "contest_start_time": 1579962600, "contest_duration": 5400, "user_num": 587, "question_slugs": ["rank-transform-of-an-array", "break-a-palindrome", "sort-the-matrix-diagonally", "reverse-subarray-to-maximize-array-value"]}, {"contest_title": "\u7b2c 19 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 19", "contest_title_slug": "biweekly-contest-19", "contest_id": 146, "contest_start_time": 1581172200, "contest_duration": 5400, "user_num": 1120, "question_slugs": ["number-of-steps-to-reduce-a-number-to-zero", "number-of-sub-arrays-of-size-k-and-average-greater-than-or-equal-to-threshold", "angle-between-hands-of-a-clock", "jump-game-iv"]}, {"contest_title": "\u7b2c 20 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 20", "contest_title_slug": "biweekly-contest-20", "contest_id": 149, "contest_start_time": 1582381800, "contest_duration": 5400, "user_num": 1541, "question_slugs": ["sort-integers-by-the-number-of-1-bits", "apply-discount-every-n-orders", "number-of-substrings-containing-all-three-characters", "count-all-valid-pickup-and-delivery-options"]}, {"contest_title": "\u7b2c 21 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 21", "contest_title_slug": "biweekly-contest-21", "contest_id": 157, "contest_start_time": 1583591400, "contest_duration": 5400, "user_num": 1913, "question_slugs": ["increasing-decreasing-string", "find-the-longest-substring-containing-vowels-in-even-counts", "longest-zigzag-path-in-a-binary-tree", "maximum-sum-bst-in-binary-tree"]}, {"contest_title": "\u7b2c 22 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 22", "contest_title_slug": "biweekly-contest-22", "contest_id": 163, "contest_start_time": 1584801000, "contest_duration": 5400, "user_num": 2042, "question_slugs": ["find-the-distance-value-between-two-arrays", "cinema-seat-allocation", "sort-integers-by-the-power-value", "pizza-with-3n-slices"]}, {"contest_title": "\u7b2c 23 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 23", "contest_title_slug": "biweekly-contest-23", "contest_id": 169, "contest_start_time": 1586010600, "contest_duration": 5400, "user_num": 2045, "question_slugs": ["count-largest-group", "construct-k-palindrome-strings", "circle-and-rectangle-overlapping", "reducing-dishes"]}, {"contest_title": "\u7b2c 24 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 24", "contest_title_slug": "biweekly-contest-24", "contest_id": 178, "contest_start_time": 1587220200, "contest_duration": 5400, "user_num": 1898, "question_slugs": ["minimum-value-to-get-positive-step-by-step-sum", "find-the-minimum-number-of-fibonacci-numbers-whose-sum-is-k", "the-k-th-lexicographical-string-of-all-happy-strings-of-length-n", "restore-the-array"]}, {"contest_title": "\u7b2c 25 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 25", "contest_title_slug": "biweekly-contest-25", "contest_id": 192, "contest_start_time": 1588429800, "contest_duration": 5400, "user_num": 1832, "question_slugs": ["kids-with-the-greatest-number-of-candies", "max-difference-you-can-get-from-changing-an-integer", "check-if-a-string-can-break-another-string", "number-of-ways-to-wear-different-hats-to-each-other"]}, {"contest_title": "\u7b2c 26 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 26", "contest_title_slug": "biweekly-contest-26", "contest_id": 198, "contest_start_time": 1589639400, "contest_duration": 5400, "user_num": 1971, "question_slugs": ["consecutive-characters", "simplified-fractions", "count-good-nodes-in-binary-tree", "form-largest-integer-with-digits-that-add-up-to-target"]}, {"contest_title": "\u7b2c 27 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 27", "contest_title_slug": "biweekly-contest-27", "contest_id": 204, "contest_start_time": 1590849000, "contest_duration": 5400, "user_num": 1966, "question_slugs": ["make-two-arrays-equal-by-reversing-subarrays", "check-if-a-string-contains-all-binary-codes-of-size-k", "course-schedule-iv", "cherry-pickup-ii"]}, {"contest_title": "\u7b2c 28 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 28", "contest_title_slug": "biweekly-contest-28", "contest_id": 210, "contest_start_time": 1592058600, "contest_duration": 5400, "user_num": 2144, "question_slugs": ["final-prices-with-a-special-discount-in-a-shop", "subrectangle-queries", "find-two-non-overlapping-sub-arrays-each-with-target-sum", "allocate-mailboxes"]}, {"contest_title": "\u7b2c 29 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 29", "contest_title_slug": "biweekly-contest-29", "contest_id": 216, "contest_start_time": 1593268200, "contest_duration": 5400, "user_num": 2260, "question_slugs": ["average-salary-excluding-the-minimum-and-maximum-salary", "the-kth-factor-of-n", "longest-subarray-of-1s-after-deleting-one-element", "parallel-courses-ii"]}, {"contest_title": "\u7b2c 30 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 30", "contest_title_slug": "biweekly-contest-30", "contest_id": 222, "contest_start_time": 1594477800, "contest_duration": 5400, "user_num": 2545, "question_slugs": ["reformat-date", "range-sum-of-sorted-subarray-sums", "minimum-difference-between-largest-and-smallest-value-in-three-moves", "stone-game-iv"]}, {"contest_title": "\u7b2c 31 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 31", "contest_title_slug": "biweekly-contest-31", "contest_id": 232, "contest_start_time": 1595687400, "contest_duration": 5400, "user_num": 2767, "question_slugs": ["count-odd-numbers-in-an-interval-range", "number-of-sub-arrays-with-odd-sum", "number-of-good-ways-to-split-a-string", "minimum-number-of-increments-on-subarrays-to-form-a-target-array"]}, {"contest_title": "\u7b2c 32 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 32", "contest_title_slug": "biweekly-contest-32", "contest_id": 237, "contest_start_time": 1596897000, "contest_duration": 5400, "user_num": 2957, "question_slugs": ["kth-missing-positive-number", "can-convert-string-in-k-moves", "minimum-insertions-to-balance-a-parentheses-string", "find-longest-awesome-substring"]}, {"contest_title": "\u7b2c 33 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 33", "contest_title_slug": "biweekly-contest-33", "contest_id": 241, "contest_start_time": 1598106600, "contest_duration": 5400, "user_num": 3304, "question_slugs": ["thousand-separator", "minimum-number-of-vertices-to-reach-all-nodes", "minimum-numbers-of-function-calls-to-make-target-array", "detect-cycles-in-2d-grid"]}, {"contest_title": "\u7b2c 34 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 34", "contest_title_slug": "biweekly-contest-34", "contest_id": 256, "contest_start_time": 1599316200, "contest_duration": 5400, "user_num": 2842, "question_slugs": ["matrix-diagonal-sum", "number-of-ways-to-split-a-string", "shortest-subarray-to-be-removed-to-make-array-sorted", "count-all-possible-routes"]}, {"contest_title": "\u7b2c 35 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 35", "contest_title_slug": "biweekly-contest-35", "contest_id": 266, "contest_start_time": 1600525800, "contest_duration": 5400, "user_num": 2839, "question_slugs": ["sum-of-all-odd-length-subarrays", "maximum-sum-obtained-of-any-permutation", "make-sum-divisible-by-p", "strange-printer-ii"]}, {"contest_title": "\u7b2c 36 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 36", "contest_title_slug": "biweekly-contest-36", "contest_id": 288, "contest_start_time": 1601735400, "contest_duration": 5400, "user_num": 2204, "question_slugs": ["design-parking-system", "alert-using-same-key-card-three-or-more-times-in-a-one-hour-period", "find-valid-matrix-given-row-and-column-sums", "find-servers-that-handled-most-number-of-requests"]}, {"contest_title": "\u7b2c 37 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 37", "contest_title_slug": "biweekly-contest-37", "contest_id": 294, "contest_start_time": 1602945000, "contest_duration": 5400, "user_num": 2104, "question_slugs": ["mean-of-array-after-removing-some-elements", "coordinate-with-maximum-network-quality", "number-of-sets-of-k-non-overlapping-line-segments", "fancy-sequence"]}, {"contest_title": "\u7b2c 38 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 38", "contest_title_slug": "biweekly-contest-38", "contest_id": 300, "contest_start_time": 1604154600, "contest_duration": 5400, "user_num": 2004, "question_slugs": ["sort-array-by-increasing-frequency", "widest-vertical-area-between-two-points-containing-no-points", "count-substrings-that-differ-by-one-character", "number-of-ways-to-form-a-target-string-given-a-dictionary"]}, {"contest_title": "\u7b2c 39 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 39", "contest_title_slug": "biweekly-contest-39", "contest_id": 306, "contest_start_time": 1605364200, "contest_duration": 5400, "user_num": 2069, "question_slugs": ["defuse-the-bomb", "minimum-deletions-to-make-string-balanced", "minimum-jumps-to-reach-home", "distribute-repeating-integers"]}, {"contest_title": "\u7b2c 40 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 40", "contest_title_slug": "biweekly-contest-40", "contest_id": 312, "contest_start_time": 1606573800, "contest_duration": 5400, "user_num": 1891, "question_slugs": ["maximum-repeating-substring", "merge-in-between-linked-lists", "design-front-middle-back-queue", "minimum-number-of-removals-to-make-mountain-array"]}, {"contest_title": "\u7b2c 41 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 41", "contest_title_slug": "biweekly-contest-41", "contest_id": 318, "contest_start_time": 1607783400, "contest_duration": 5400, "user_num": 1660, "question_slugs": ["count-the-number-of-consistent-strings", "sum-of-absolute-differences-in-a-sorted-array", "stone-game-vi", "delivering-boxes-from-storage-to-ports"]}, {"contest_title": "\u7b2c 42 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 42", "contest_title_slug": "biweekly-contest-42", "contest_id": 325, "contest_start_time": 1608993000, "contest_duration": 5400, "user_num": 1578, "question_slugs": ["number-of-students-unable-to-eat-lunch", "average-waiting-time", "maximum-binary-string-after-change", "minimum-adjacent-swaps-for-k-consecutive-ones"]}, {"contest_title": "\u7b2c 43 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 43", "contest_title_slug": "biweekly-contest-43", "contest_id": 331, "contest_start_time": 1610202600, "contest_duration": 5400, "user_num": 1631, "question_slugs": ["calculate-money-in-leetcode-bank", "maximum-score-from-removing-substrings", "construct-the-lexicographically-largest-valid-sequence", "number-of-ways-to-reconstruct-a-tree"]}, {"contest_title": "\u7b2c 44 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 44", "contest_title_slug": "biweekly-contest-44", "contest_id": 337, "contest_start_time": 1611412200, "contest_duration": 5400, "user_num": 1826, "question_slugs": ["find-the-highest-altitude", "minimum-number-of-people-to-teach", "decode-xored-permutation", "count-ways-to-make-array-with-product"]}, {"contest_title": "\u7b2c 45 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 45", "contest_title_slug": "biweekly-contest-45", "contest_id": 343, "contest_start_time": 1612621800, "contest_duration": 5400, "user_num": 1676, "question_slugs": ["sum-of-unique-elements", "maximum-absolute-sum-of-any-subarray", "minimum-length-of-string-after-deleting-similar-ends", "maximum-number-of-events-that-can-be-attended-ii"]}, {"contest_title": "\u7b2c 46 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 46", "contest_title_slug": "biweekly-contest-46", "contest_id": 349, "contest_start_time": 1613831400, "contest_duration": 5400, "user_num": 1647, "question_slugs": ["longest-nice-substring", "form-array-by-concatenating-subarrays-of-another-array", "map-of-highest-peak", "tree-of-coprimes"]}, {"contest_title": "\u7b2c 47 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 47", "contest_title_slug": "biweekly-contest-47", "contest_id": 355, "contest_start_time": 1615041000, "contest_duration": 5400, "user_num": 3085, "question_slugs": ["find-nearest-point-that-has-the-same-x-or-y-coordinate", "check-if-number-is-a-sum-of-powers-of-three", "sum-of-beauty-of-all-substrings", "count-pairs-of-nodes"]}, {"contest_title": "\u7b2c 48 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 48", "contest_title_slug": "biweekly-contest-48", "contest_id": 362, "contest_start_time": 1616250600, "contest_duration": 5400, "user_num": 2853, "question_slugs": ["second-largest-digit-in-a-string", "design-authentication-manager", "maximum-number-of-consecutive-values-you-can-make", "maximize-score-after-n-operations"]}, {"contest_title": "\u7b2c 49 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 49", "contest_title_slug": "biweekly-contest-49", "contest_id": 374, "contest_start_time": 1617460200, "contest_duration": 5400, "user_num": 3193, "question_slugs": ["determine-color-of-a-chessboard-square", "sentence-similarity-iii", "count-nice-pairs-in-an-array", "maximum-number-of-groups-getting-fresh-donuts"]}, {"contest_title": "\u7b2c 50 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 50", "contest_title_slug": "biweekly-contest-50", "contest_id": 390, "contest_start_time": 1618669800, "contest_duration": 5400, "user_num": 3608, "question_slugs": ["minimum-operations-to-make-the-array-increasing", "queries-on-number-of-points-inside-a-circle", "maximum-xor-for-each-query", "minimum-number-of-operations-to-make-string-sorted"]}, {"contest_title": "\u7b2c 51 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 51", "contest_title_slug": "biweekly-contest-51", "contest_id": 396, "contest_start_time": 1619879400, "contest_duration": 5400, "user_num": 2675, "question_slugs": ["replace-all-digits-with-characters", "seat-reservation-manager", "maximum-element-after-decreasing-and-rearranging", "closest-room"]}, {"contest_title": "\u7b2c 52 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 52", "contest_title_slug": "biweekly-contest-52", "contest_id": 402, "contest_start_time": 1621089000, "contest_duration": 5400, "user_num": 2930, "question_slugs": ["sorting-the-sentence", "incremental-memory-leak", "rotating-the-box", "sum-of-floored-pairs"]}, {"contest_title": "\u7b2c 53 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 53", "contest_title_slug": "biweekly-contest-53", "contest_id": 408, "contest_start_time": 1622298600, "contest_duration": 5400, "user_num": 3069, "question_slugs": ["substrings-of-size-three-with-distinct-characters", "minimize-maximum-pair-sum-in-array", "get-biggest-three-rhombus-sums-in-a-grid", "minimum-xor-sum-of-two-arrays"]}, {"contest_title": "\u7b2c 54 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 54", "contest_title_slug": "biweekly-contest-54", "contest_id": 414, "contest_start_time": 1623508200, "contest_duration": 5400, "user_num": 2479, "question_slugs": ["check-if-all-the-integers-in-a-range-are-covered", "find-the-student-that-will-replace-the-chalk", "largest-magic-square", "minimum-cost-to-change-the-final-value-of-expression"]}, {"contest_title": "\u7b2c 55 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 55", "contest_title_slug": "biweekly-contest-55", "contest_id": 421, "contest_start_time": 1624717800, "contest_duration": 5400, "user_num": 3277, "question_slugs": ["remove-one-element-to-make-the-array-strictly-increasing", "remove-all-occurrences-of-a-substring", "maximum-alternating-subsequence-sum", "design-movie-rental-system"]}, {"contest_title": "\u7b2c 56 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 56", "contest_title_slug": "biweekly-contest-56", "contest_id": 429, "contest_start_time": 1625927400, "contest_duration": 5400, "user_num": 2760, "question_slugs": ["count-square-sum-triples", "nearest-exit-from-entrance-in-maze", "sum-game", "minimum-cost-to-reach-destination-in-time"]}, {"contest_title": "\u7b2c 57 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 57", "contest_title_slug": "biweekly-contest-57", "contest_id": 435, "contest_start_time": 1627137000, "contest_duration": 5400, "user_num": 2933, "question_slugs": ["check-if-all-characters-have-equal-number-of-occurrences", "the-number-of-the-smallest-unoccupied-chair", "describe-the-painting", "number-of-visible-people-in-a-queue"]}, {"contest_title": "\u7b2c 58 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 58", "contest_title_slug": "biweekly-contest-58", "contest_id": 441, "contest_start_time": 1628346600, "contest_duration": 5400, "user_num": 2889, "question_slugs": ["delete-characters-to-make-fancy-string", "check-if-move-is-legal", "minimum-total-space-wasted-with-k-resizing-operations", "maximum-product-of-the-length-of-two-palindromic-substrings"]}, {"contest_title": "\u7b2c 59 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 59", "contest_title_slug": "biweekly-contest-59", "contest_id": 448, "contest_start_time": 1629556200, "contest_duration": 5400, "user_num": 3030, "question_slugs": ["minimum-time-to-type-word-using-special-typewriter", "maximum-matrix-sum", "number-of-ways-to-arrive-at-destination", "number-of-ways-to-separate-numbers"]}, {"contest_title": "\u7b2c 60 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 60", "contest_title_slug": "biweekly-contest-60", "contest_id": 461, "contest_start_time": 1630765800, "contest_duration": 5400, "user_num": 2848, "question_slugs": ["find-the-middle-index-in-array", "find-all-groups-of-farmland", "operations-on-tree", "the-number-of-good-subsets"]}, {"contest_title": "\u7b2c 61 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 61", "contest_title_slug": "biweekly-contest-61", "contest_id": 467, "contest_start_time": 1631975400, "contest_duration": 5400, "user_num": 2534, "question_slugs": ["count-number-of-pairs-with-absolute-difference-k", "find-original-array-from-doubled-array", "maximum-earnings-from-taxi", "minimum-number-of-operations-to-make-array-continuous"]}, {"contest_title": "\u7b2c 62 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 62", "contest_title_slug": "biweekly-contest-62", "contest_id": 477, "contest_start_time": 1633185000, "contest_duration": 5400, "user_num": 2619, "question_slugs": ["convert-1d-array-into-2d-array", "number-of-pairs-of-strings-with-concatenation-equal-to-target", "maximize-the-confusion-of-an-exam", "maximum-number-of-ways-to-partition-an-array"]}, {"contest_title": "\u7b2c 63 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 63", "contest_title_slug": "biweekly-contest-63", "contest_id": 484, "contest_start_time": 1634394600, "contest_duration": 5400, "user_num": 2828, "question_slugs": ["minimum-number-of-moves-to-seat-everyone", "remove-colored-pieces-if-both-neighbors-are-the-same-color", "the-time-when-the-network-becomes-idle", "kth-smallest-product-of-two-sorted-arrays"]}, {"contest_title": "\u7b2c 64 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 64", "contest_title_slug": "biweekly-contest-64", "contest_id": 490, "contest_start_time": 1635604200, "contest_duration": 5400, "user_num": 2838, "question_slugs": ["kth-distinct-string-in-an-array", "two-best-non-overlapping-events", "plates-between-candles", "number-of-valid-move-combinations-on-chessboard"]}, {"contest_title": "\u7b2c 65 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 65", "contest_title_slug": "biweekly-contest-65", "contest_id": 497, "contest_start_time": 1636813800, "contest_duration": 5400, "user_num": 2676, "question_slugs": ["check-whether-two-strings-are-almost-equivalent", "walking-robot-simulation-ii", "most-beautiful-item-for-each-query", "maximum-number-of-tasks-you-can-assign"]}, {"contest_title": "\u7b2c 66 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 66", "contest_title_slug": "biweekly-contest-66", "contest_id": 503, "contest_start_time": 1638023400, "contest_duration": 5400, "user_num": 2803, "question_slugs": ["count-common-words-with-one-occurrence", "minimum-number-of-food-buckets-to-feed-the-hamsters", "minimum-cost-homecoming-of-a-robot-in-a-grid", "count-fertile-pyramids-in-a-land"]}, {"contest_title": "\u7b2c 67 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 67", "contest_title_slug": "biweekly-contest-67", "contest_id": 509, "contest_start_time": 1639233000, "contest_duration": 5400, "user_num": 2923, "question_slugs": ["find-subsequence-of-length-k-with-the-largest-sum", "find-good-days-to-rob-the-bank", "detonate-the-maximum-bombs", "sequentially-ordinal-rank-tracker"]}, {"contest_title": "\u7b2c 68 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 68", "contest_title_slug": "biweekly-contest-68", "contest_id": 515, "contest_start_time": 1640442600, "contest_duration": 5400, "user_num": 2854, "question_slugs": ["maximum-number-of-words-found-in-sentences", "find-all-possible-recipes-from-given-supplies", "check-if-a-parentheses-string-can-be-valid", "abbreviating-the-product-of-a-range"]}, {"contest_title": "\u7b2c 69 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 69", "contest_title_slug": "biweekly-contest-69", "contest_id": 521, "contest_start_time": 1641652200, "contest_duration": 5400, "user_num": 3360, "question_slugs": ["capitalize-the-title", "maximum-twin-sum-of-a-linked-list", "longest-palindrome-by-concatenating-two-letter-words", "stamping-the-grid"]}, {"contest_title": "\u7b2c 70 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 70", "contest_title_slug": "biweekly-contest-70", "contest_id": 527, "contest_start_time": 1642861800, "contest_duration": 5400, "user_num": 3640, "question_slugs": ["minimum-cost-of-buying-candies-with-discount", "count-the-hidden-sequences", "k-highest-ranked-items-within-a-price-range", "number-of-ways-to-divide-a-long-corridor"]}, {"contest_title": "\u7b2c 71 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 71", "contest_title_slug": "biweekly-contest-71", "contest_id": 533, "contest_start_time": 1644071400, "contest_duration": 5400, "user_num": 3028, "question_slugs": ["minimum-sum-of-four-digit-number-after-splitting-digits", "partition-array-according-to-given-pivot", "minimum-cost-to-set-cooking-time", "minimum-difference-in-sums-after-removal-of-elements"]}, {"contest_title": "\u7b2c 72 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 72", "contest_title_slug": "biweekly-contest-72", "contest_id": 539, "contest_start_time": 1645281000, "contest_duration": 5400, "user_num": 4400, "question_slugs": ["count-equal-and-divisible-pairs-in-an-array", "find-three-consecutive-integers-that-sum-to-a-given-number", "maximum-split-of-positive-even-integers", "count-good-triplets-in-an-array"]}, {"contest_title": "\u7b2c 73 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 73", "contest_title_slug": "biweekly-contest-73", "contest_id": 545, "contest_start_time": 1646490600, "contest_duration": 5400, "user_num": 5132, "question_slugs": ["most-frequent-number-following-key-in-an-array", "sort-the-jumbled-numbers", "all-ancestors-of-a-node-in-a-directed-acyclic-graph", "minimum-number-of-moves-to-make-palindrome"]}, {"contest_title": "\u7b2c 74 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 74", "contest_title_slug": "biweekly-contest-74", "contest_id": 554, "contest_start_time": 1647700200, "contest_duration": 5400, "user_num": 5442, "question_slugs": ["divide-array-into-equal-pairs", "maximize-number-of-subsequences-in-a-string", "minimum-operations-to-halve-array-sum", "minimum-white-tiles-after-covering-with-carpets"]}, {"contest_title": "\u7b2c 75 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 75", "contest_title_slug": "biweekly-contest-75", "contest_id": 563, "contest_start_time": 1648909800, "contest_duration": 5400, "user_num": 4335, "question_slugs": ["minimum-bit-flips-to-convert-number", "find-triangular-sum-of-an-array", "number-of-ways-to-select-buildings", "sum-of-scores-of-built-strings"]}, {"contest_title": "\u7b2c 76 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 76", "contest_title_slug": "biweekly-contest-76", "contest_id": 572, "contest_start_time": 1650119400, "contest_duration": 5400, "user_num": 4477, "question_slugs": ["find-closest-number-to-zero", "number-of-ways-to-buy-pens-and-pencils", "design-an-atm-machine", "maximum-score-of-a-node-sequence"]}, {"contest_title": "\u7b2c 77 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 77", "contest_title_slug": "biweekly-contest-77", "contest_id": 581, "contest_start_time": 1651329000, "contest_duration": 5400, "user_num": 4211, "question_slugs": ["count-prefixes-of-a-given-string", "minimum-average-difference", "count-unguarded-cells-in-the-grid", "escape-the-spreading-fire"]}, {"contest_title": "\u7b2c 78 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 78", "contest_title_slug": "biweekly-contest-78", "contest_id": 590, "contest_start_time": 1652538600, "contest_duration": 5400, "user_num": 4347, "question_slugs": ["find-the-k-beauty-of-a-number", "number-of-ways-to-split-array", "maximum-white-tiles-covered-by-a-carpet", "substring-with-largest-variance"]}, {"contest_title": "\u7b2c 79 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 79", "contest_title_slug": "biweekly-contest-79", "contest_id": 598, "contest_start_time": 1653748200, "contest_duration": 5400, "user_num": 4250, "question_slugs": ["check-if-number-has-equal-digit-count-and-digit-value", "sender-with-largest-word-count", "maximum-total-importance-of-roads", "booking-concert-tickets-in-groups"]}, {"contest_title": "\u7b2c 80 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 80", "contest_title_slug": "biweekly-contest-80", "contest_id": 608, "contest_start_time": 1654957800, "contest_duration": 5400, "user_num": 3949, "question_slugs": ["strong-password-checker-ii", "successful-pairs-of-spells-and-potions", "match-substring-after-replacement", "count-subarrays-with-score-less-than-k"]}, {"contest_title": "\u7b2c 81 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 81", "contest_title_slug": "biweekly-contest-81", "contest_id": 614, "contest_start_time": 1656167400, "contest_duration": 5400, "user_num": 3847, "question_slugs": ["count-asterisks", "count-unreachable-pairs-of-nodes-in-an-undirected-graph", "maximum-xor-after-operations", "number-of-distinct-roll-sequences"]}, {"contest_title": "\u7b2c 82 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 82", "contest_title_slug": "biweekly-contest-82", "contest_id": 646, "contest_start_time": 1657377000, "contest_duration": 5400, "user_num": 4144, "question_slugs": ["evaluate-boolean-binary-tree", "the-latest-time-to-catch-a-bus", "minimum-sum-of-squared-difference", "subarray-with-elements-greater-than-varying-threshold"]}, {"contest_title": "\u7b2c 83 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 83", "contest_title_slug": "biweekly-contest-83", "contest_id": 652, "contest_start_time": 1658586600, "contest_duration": 5400, "user_num": 4437, "question_slugs": ["best-poker-hand", "number-of-zero-filled-subarrays", "design-a-number-container-system", "shortest-impossible-sequence-of-rolls"]}, {"contest_title": "\u7b2c 84 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 84", "contest_title_slug": "biweekly-contest-84", "contest_id": 658, "contest_start_time": 1659796200, "contest_duration": 5400, "user_num": 4574, "question_slugs": ["merge-similar-items", "count-number-of-bad-pairs", "task-scheduler-ii", "minimum-replacements-to-sort-the-array"]}, {"contest_title": "\u7b2c 85 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 85", "contest_title_slug": "biweekly-contest-85", "contest_id": 668, "contest_start_time": 1661005800, "contest_duration": 5400, "user_num": 4193, "question_slugs": ["minimum-recolors-to-get-k-consecutive-black-blocks", "time-needed-to-rearrange-a-binary-string", "shifting-letters-ii", "maximum-segment-sum-after-removals"]}, {"contest_title": "\u7b2c 86 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 86", "contest_title_slug": "biweekly-contest-86", "contest_id": 688, "contest_start_time": 1662215400, "contest_duration": 5400, "user_num": 4401, "question_slugs": ["find-subarrays-with-equal-sum", "strictly-palindromic-number", "maximum-rows-covered-by-columns", "maximum-number-of-robots-within-budget"]}, {"contest_title": "\u7b2c 87 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 87", "contest_title_slug": "biweekly-contest-87", "contest_id": 703, "contest_start_time": 1663425000, "contest_duration": 5400, "user_num": 4005, "question_slugs": ["count-days-spent-together", "maximum-matching-of-players-with-trainers", "smallest-subarrays-with-maximum-bitwise-or", "minimum-money-required-before-transactions"]}, {"contest_title": "\u7b2c 88 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 88", "contest_title_slug": "biweekly-contest-88", "contest_id": 745, "contest_start_time": 1664634600, "contest_duration": 5400, "user_num": 3905, "question_slugs": ["remove-letter-to-equalize-frequency", "longest-uploaded-prefix", "bitwise-xor-of-all-pairings", "number-of-pairs-satisfying-inequality"]}, {"contest_title": "\u7b2c 89 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 89", "contest_title_slug": "biweekly-contest-89", "contest_id": 755, "contest_start_time": 1665844200, "contest_duration": 5400, "user_num": 3984, "question_slugs": ["number-of-valid-clock-times", "range-product-queries-of-powers", "minimize-maximum-of-array", "create-components-with-same-value"]}, {"contest_title": "\u7b2c 90 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 90", "contest_title_slug": "biweekly-contest-90", "contest_id": 763, "contest_start_time": 1667053800, "contest_duration": 5400, "user_num": 3624, "question_slugs": ["odd-string-difference", "words-within-two-edits-of-dictionary", "destroy-sequential-targets", "next-greater-element-iv"]}, {"contest_title": "\u7b2c 91 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 91", "contest_title_slug": "biweekly-contest-91", "contest_id": 770, "contest_start_time": 1668263400, "contest_duration": 5400, "user_num": 3535, "question_slugs": ["number-of-distinct-averages", "count-ways-to-build-good-strings", "most-profitable-path-in-a-tree", "split-message-based-on-limit"]}, {"contest_title": "\u7b2c 92 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 92", "contest_title_slug": "biweekly-contest-92", "contest_id": 776, "contest_start_time": 1669473000, "contest_duration": 5400, "user_num": 3055, "question_slugs": ["minimum-cuts-to-divide-a-circle", "difference-between-ones-and-zeros-in-row-and-column", "minimum-penalty-for-a-shop", "count-palindromic-subsequences"]}, {"contest_title": "\u7b2c 93 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 93", "contest_title_slug": "biweekly-contest-93", "contest_id": 782, "contest_start_time": 1670682600, "contest_duration": 5400, "user_num": 2929, "question_slugs": ["maximum-value-of-a-string-in-an-array", "maximum-star-sum-of-a-graph", "frog-jump-ii", "minimum-total-cost-to-make-arrays-unequal"]}, {"contest_title": "\u7b2c 94 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 94", "contest_title_slug": "biweekly-contest-94", "contest_id": 789, "contest_start_time": 1671892200, "contest_duration": 5400, "user_num": 2298, "question_slugs": ["maximum-enemy-forts-that-can-be-captured", "reward-top-k-students", "minimize-the-maximum-of-two-arrays", "count-anagrams"]}, {"contest_title": "\u7b2c 95 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 95", "contest_title_slug": "biweekly-contest-95", "contest_id": 798, "contest_start_time": 1673101800, "contest_duration": 5400, "user_num": 2880, "question_slugs": ["categorize-box-according-to-criteria", "find-consecutive-integers-from-a-data-stream", "find-xor-beauty-of-array", "maximize-the-minimum-powered-city"]}, {"contest_title": "\u7b2c 96 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 96", "contest_title_slug": "biweekly-contest-96", "contest_id": 804, "contest_start_time": 1674311400, "contest_duration": 5400, "user_num": 2103, "question_slugs": ["minimum-common-value", "minimum-operations-to-make-array-equal-ii", "maximum-subsequence-score", "check-if-point-is-reachable"]}, {"contest_title": "\u7b2c 97 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 97", "contest_title_slug": "biweekly-contest-97", "contest_id": 810, "contest_start_time": 1675521000, "contest_duration": 5400, "user_num": 2631, "question_slugs": ["separate-the-digits-in-an-array", "maximum-number-of-integers-to-choose-from-a-range-i", "maximize-win-from-two-segments", "disconnect-path-in-a-binary-matrix-by-at-most-one-flip"]}, {"contest_title": "\u7b2c 98 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 98", "contest_title_slug": "biweekly-contest-98", "contest_id": 816, "contest_start_time": 1676730600, "contest_duration": 5400, "user_num": 3250, "question_slugs": ["maximum-difference-by-remapping-a-digit", "minimum-score-by-changing-two-elements", "minimum-impossible-or", "handling-sum-queries-after-update"]}, {"contest_title": "\u7b2c 99 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 99", "contest_title_slug": "biweekly-contest-99", "contest_id": 822, "contest_start_time": 1677940200, "contest_duration": 5400, "user_num": 3467, "question_slugs": ["split-with-minimum-sum", "count-total-number-of-colored-cells", "count-ways-to-group-overlapping-ranges", "count-number-of-possible-root-nodes"]}, {"contest_title": "\u7b2c 100 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 100", "contest_title_slug": "biweekly-contest-100", "contest_id": 832, "contest_start_time": 1679149800, "contest_duration": 5400, "user_num": 3639, "question_slugs": ["distribute-money-to-maximum-children", "maximize-greatness-of-an-array", "find-score-of-an-array-after-marking-all-elements", "minimum-time-to-repair-cars"]}, {"contest_title": "\u7b2c 101 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 101", "contest_title_slug": "biweekly-contest-101", "contest_id": 842, "contest_start_time": 1680359400, "contest_duration": 5400, "user_num": 3353, "question_slugs": ["form-smallest-number-from-two-digit-arrays", "find-the-substring-with-maximum-cost", "make-k-subarray-sums-equal", "shortest-cycle-in-a-graph"]}, {"contest_title": "\u7b2c 102 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 102", "contest_title_slug": "biweekly-contest-102", "contest_id": 853, "contest_start_time": 1681569000, "contest_duration": 5400, "user_num": 3058, "question_slugs": ["find-the-width-of-columns-of-a-grid", "find-the-score-of-all-prefixes-of-an-array", "cousins-in-binary-tree-ii", "design-graph-with-shortest-path-calculator"]}, {"contest_title": "\u7b2c 103 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 103", "contest_title_slug": "biweekly-contest-103", "contest_id": 859, "contest_start_time": 1682778600, "contest_duration": 5400, "user_num": 2299, "question_slugs": ["maximum-sum-with-exactly-k-elements", "find-the-prefix-common-array-of-two-arrays", "maximum-number-of-fish-in-a-grid", "make-array-empty"]}, {"contest_title": "\u7b2c 104 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 104", "contest_title_slug": "biweekly-contest-104", "contest_id": 866, "contest_start_time": 1683988200, "contest_duration": 5400, "user_num": 2519, "question_slugs": ["number-of-senior-citizens", "sum-in-a-matrix", "maximum-or", "power-of-heroes"]}, {"contest_title": "\u7b2c 105 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 105", "contest_title_slug": "biweekly-contest-105", "contest_id": 873, "contest_start_time": 1685197800, "contest_duration": 5400, "user_num": 2604, "question_slugs": ["buy-two-chocolates", "extra-characters-in-a-string", "maximum-strength-of-a-group", "greatest-common-divisor-traversal"]}, {"contest_title": "\u7b2c 106 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 106", "contest_title_slug": "biweekly-contest-106", "contest_id": 879, "contest_start_time": 1686407400, "contest_duration": 5400, "user_num": 2346, "question_slugs": ["check-if-the-number-is-fascinating", "find-the-longest-semi-repetitive-substring", "movement-of-robots", "find-a-good-subset-of-the-matrix"]}, {"contest_title": "\u7b2c 107 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 107", "contest_title_slug": "biweekly-contest-107", "contest_id": 885, "contest_start_time": 1687617000, "contest_duration": 5400, "user_num": 1870, "question_slugs": ["find-maximum-number-of-string-pairs", "construct-the-longest-new-string", "decremental-string-concatenation", "count-zero-request-servers"]}, {"contest_title": "\u7b2c 108 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 108", "contest_title_slug": "biweekly-contest-108", "contest_id": 891, "contest_start_time": 1688826600, "contest_duration": 5400, "user_num": 2349, "question_slugs": ["longest-alternating-subarray", "relocate-marbles", "partition-string-into-minimum-beautiful-substrings", "number-of-black-blocks"]}, {"contest_title": "\u7b2c 109 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 109", "contest_title_slug": "biweekly-contest-109", "contest_id": 897, "contest_start_time": 1690036200, "contest_duration": 5400, "user_num": 2461, "question_slugs": ["check-if-array-is-good", "sort-vowels-in-a-string", "visit-array-positions-to-maximize-score", "ways-to-express-an-integer-as-sum-of-powers"]}, {"contest_title": "\u7b2c 110 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 110", "contest_title_slug": "biweekly-contest-110", "contest_id": 903, "contest_start_time": 1691245800, "contest_duration": 5400, "user_num": 2546, "question_slugs": ["account-balance-after-rounded-purchase", "insert-greatest-common-divisors-in-linked-list", "minimum-seconds-to-equalize-a-circular-array", "minimum-time-to-make-array-sum-at-most-x"]}, {"contest_title": "\u7b2c 111 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 111", "contest_title_slug": "biweekly-contest-111", "contest_id": 909, "contest_start_time": 1692455400, "contest_duration": 5400, "user_num": 2787, "question_slugs": ["count-pairs-whose-sum-is-less-than-target", "make-string-a-subsequence-using-cyclic-increments", "sorting-three-groups", "number-of-beautiful-integers-in-the-range"]}, {"contest_title": "\u7b2c 112 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 112", "contest_title_slug": "biweekly-contest-112", "contest_id": 917, "contest_start_time": 1693665000, "contest_duration": 5400, "user_num": 2900, "question_slugs": ["check-if-strings-can-be-made-equal-with-operations-i", "check-if-strings-can-be-made-equal-with-operations-ii", "maximum-sum-of-almost-unique-subarray", "count-k-subsequences-of-a-string-with-maximum-beauty"]}, {"contest_title": "\u7b2c 113 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 113", "contest_title_slug": "biweekly-contest-113", "contest_id": 923, "contest_start_time": 1694874600, "contest_duration": 5400, "user_num": 3028, "question_slugs": ["minimum-right-shifts-to-sort-the-array", "minimum-array-length-after-pair-removals", "count-pairs-of-points-with-distance-k", "minimum-edge-reversals-so-every-node-is-reachable"]}, {"contest_title": "\u7b2c 114 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 114", "contest_title_slug": "biweekly-contest-114", "contest_id": 929, "contest_start_time": 1696084200, "contest_duration": 5400, "user_num": 2406, "question_slugs": ["minimum-operations-to-collect-elements", "minimum-number-of-operations-to-make-array-empty", "split-array-into-maximum-number-of-subarrays", "maximum-number-of-k-divisible-components"]}, {"contest_title": "\u7b2c 115 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 115", "contest_title_slug": "biweekly-contest-115", "contest_id": 935, "contest_start_time": 1697293800, "contest_duration": 5400, "user_num": 2809, "question_slugs": ["last-visited-integers", "longest-unequal-adjacent-groups-subsequence-i", "longest-unequal-adjacent-groups-subsequence-ii", "count-of-sub-multisets-with-bounded-sum"]}, {"contest_title": "\u7b2c 116 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 116", "contest_title_slug": "biweekly-contest-116", "contest_id": 941, "contest_start_time": 1698503400, "contest_duration": 5400, "user_num": 2904, "question_slugs": ["subarrays-distinct-element-sum-of-squares-i", "minimum-number-of-changes-to-make-binary-string-beautiful", "length-of-the-longest-subsequence-that-sums-to-target", "subarrays-distinct-element-sum-of-squares-ii"]}, {"contest_title": "\u7b2c 117 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 117", "contest_title_slug": "biweekly-contest-117", "contest_id": 949, "contest_start_time": 1699713000, "contest_duration": 5400, "user_num": 2629, "question_slugs": ["distribute-candies-among-children-i", "distribute-candies-among-children-ii", "number-of-strings-which-can-be-rearranged-to-contain-substring", "maximum-spending-after-buying-items"]}, {"contest_title": "\u7b2c 118 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 118", "contest_title_slug": "biweekly-contest-118", "contest_id": 955, "contest_start_time": 1700922600, "contest_duration": 5400, "user_num": 2425, "question_slugs": ["find-words-containing-character", "maximize-area-of-square-hole-in-grid", "minimum-number-of-coins-for-fruits", "find-maximum-non-decreasing-array-length"]}, {"contest_title": "\u7b2c 119 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 119", "contest_title_slug": "biweekly-contest-119", "contest_id": 961, "contest_start_time": 1702132200, "contest_duration": 5400, "user_num": 2472, "question_slugs": ["find-common-elements-between-two-arrays", "remove-adjacent-almost-equal-characters", "length-of-longest-subarray-with-at-most-k-frequency", "number-of-possible-sets-of-closing-branches"]}, {"contest_title": "\u7b2c 120 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 120", "contest_title_slug": "biweekly-contest-120", "contest_id": 967, "contest_start_time": 1703341800, "contest_duration": 5400, "user_num": 2542, "question_slugs": ["count-the-number-of-incremovable-subarrays-i", "find-polygon-with-the-largest-perimeter", "count-the-number-of-incremovable-subarrays-ii", "find-number-of-coins-to-place-in-tree-nodes"]}, {"contest_title": "\u7b2c 121 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 121", "contest_title_slug": "biweekly-contest-121", "contest_id": 973, "contest_start_time": 1704551400, "contest_duration": 5400, "user_num": 2218, "question_slugs": ["smallest-missing-integer-greater-than-sequential-prefix-sum", "minimum-number-of-operations-to-make-array-xor-equal-to-k", "minimum-number-of-operations-to-make-x-and-y-equal", "count-the-number-of-powerful-integers"]}, {"contest_title": "\u7b2c 122 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 122", "contest_title_slug": "biweekly-contest-122", "contest_id": 979, "contest_start_time": 1705761000, "contest_duration": 5400, "user_num": 2547, "question_slugs": ["divide-an-array-into-subarrays-with-minimum-cost-i", "find-if-array-can-be-sorted", "minimize-length-of-array-using-operations", "divide-an-array-into-subarrays-with-minimum-cost-ii"]}, {"contest_title": "\u7b2c 123 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 123", "contest_title_slug": "biweekly-contest-123", "contest_id": 985, "contest_start_time": 1706970600, "contest_duration": 5400, "user_num": 2209, "question_slugs": ["type-of-triangle", "find-the-number-of-ways-to-place-people-i", "maximum-good-subarray-sum", "find-the-number-of-ways-to-place-people-ii"]}, {"contest_title": "\u7b2c 124 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 124", "contest_title_slug": "biweekly-contest-124", "contest_id": 991, "contest_start_time": 1708180200, "contest_duration": 5400, "user_num": 1861, "question_slugs": ["maximum-number-of-operations-with-the-same-score-i", "apply-operations-to-make-string-empty", "maximum-number-of-operations-with-the-same-score-ii", "maximize-consecutive-elements-in-an-array-after-modification"]}, {"contest_title": "\u7b2c 125 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 125", "contest_title_slug": "biweekly-contest-125", "contest_id": 997, "contest_start_time": 1709389800, "contest_duration": 5400, "user_num": 2599, "question_slugs": ["minimum-operations-to-exceed-threshold-value-i", "minimum-operations-to-exceed-threshold-value-ii", "count-pairs-of-connectable-servers-in-a-weighted-tree-network", "find-the-maximum-sum-of-node-values"]}, {"contest_title": "\u7b2c 126 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 126", "contest_title_slug": "biweekly-contest-126", "contest_id": 1003, "contest_start_time": 1710599400, "contest_duration": 5400, "user_num": 3234, "question_slugs": ["find-the-sum-of-encrypted-integers", "mark-elements-on-array-by-performing-queries", "replace-question-marks-in-string-to-minimize-its-value", "find-the-sum-of-the-power-of-all-subsequences"]}, {"contest_title": "\u7b2c 127 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 127", "contest_title_slug": "biweekly-contest-127", "contest_id": 1010, "contest_start_time": 1711809000, "contest_duration": 5400, "user_num": 2951, "question_slugs": ["shortest-subarray-with-or-at-least-k-i", "minimum-levels-to-gain-more-points", "shortest-subarray-with-or-at-least-k-ii", "find-the-sum-of-subsequence-powers"]}, {"contest_title": "\u7b2c 128 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 128", "contest_title_slug": "biweekly-contest-128", "contest_id": 1017, "contest_start_time": 1713018600, "contest_duration": 5400, "user_num": 2654, "question_slugs": ["score-of-a-string", "minimum-rectangles-to-cover-points", "minimum-time-to-visit-disappearing-nodes", "find-the-number-of-subarrays-where-boundary-elements-are-maximum"]}, {"contest_title": "\u7b2c 129 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 129", "contest_title_slug": "biweekly-contest-129", "contest_id": 1023, "contest_start_time": 1714228200, "contest_duration": 5400, "user_num": 2511, "question_slugs": ["make-a-square-with-the-same-color", "right-triangles", "find-all-possible-stable-binary-arrays-i", "find-all-possible-stable-binary-arrays-ii"]}, {"contest_title": "\u7b2c 130 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 130", "contest_title_slug": "biweekly-contest-130", "contest_id": 1029, "contest_start_time": 1715437800, "contest_duration": 5400, "user_num": 2604, "question_slugs": ["check-if-grid-satisfies-conditions", "maximum-points-inside-the-square", "minimum-substring-partition-of-equal-character-frequency", "find-products-of-elements-of-big-array"]}, {"contest_title": "\u7b2c 131 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 131", "contest_title_slug": "biweekly-contest-131", "contest_id": 1035, "contest_start_time": 1716647400, "contest_duration": 5400, "user_num": 2537, "question_slugs": ["find-the-xor-of-numbers-which-appear-twice", "find-occurrences-of-an-element-in-an-array", "find-the-number-of-distinct-colors-among-the-balls", "block-placement-queries"]}, {"contest_title": "\u7b2c 132 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 132", "contest_title_slug": "biweekly-contest-132", "contest_id": 1042, "contest_start_time": 1717857000, "contest_duration": 5400, "user_num": 2457, "question_slugs": ["clear-digits", "find-the-first-player-to-win-k-games-in-a-row", "find-the-maximum-length-of-a-good-subsequence-i", "find-the-maximum-length-of-a-good-subsequence-ii"]}, {"contest_title": "\u7b2c 133 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 133", "contest_title_slug": "biweekly-contest-133", "contest_id": 1048, "contest_start_time": 1719066600, "contest_duration": 5400, "user_num": 2326, "question_slugs": ["find-minimum-operations-to-make-all-elements-divisible-by-three", "minimum-operations-to-make-binary-array-elements-equal-to-one-i", "minimum-operations-to-make-binary-array-elements-equal-to-one-ii", "count-the-number-of-inversions"]}, {"contest_title": "\u7b2c 134 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 134", "contest_title_slug": "biweekly-contest-134", "contest_id": 1055, "contest_start_time": 1720276200, "contest_duration": 5400, "user_num": 2411, "question_slugs": ["alternating-groups-i", "maximum-points-after-enemy-battles", "alternating-groups-ii", "number-of-subarrays-with-and-value-of-k"]}, {"contest_title": "\u7b2c 135 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 135", "contest_title_slug": "biweekly-contest-135", "contest_id": 1061, "contest_start_time": 1721485800, "contest_duration": 5400, "user_num": 2260, "question_slugs": ["find-the-winning-player-in-coin-game", "minimum-length-of-string-after-operations", "minimum-array-changes-to-make-differences-equal", "maximum-score-from-grid-operations"]}, {"contest_title": "\u7b2c 136 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 136", "contest_title_slug": "biweekly-contest-136", "contest_id": 1068, "contest_start_time": 1722695400, "contest_duration": 5400, "user_num": 2418, "question_slugs": ["find-the-number-of-winning-players", "minimum-number-of-flips-to-make-binary-grid-palindromic-i", "minimum-number-of-flips-to-make-binary-grid-palindromic-ii", "time-taken-to-mark-all-nodes"]}] \ No newline at end of file +[{"contest_title": "\u7b2c 83 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 83", "contest_title_slug": "weekly-contest-83", "contest_id": 5, "contest_start_time": 1525570200, "contest_duration": 5400, "user_num": 58, "question_slugs": ["positions-of-large-groups", "masking-personal-information", "consecutive-numbers-sum", "count-unique-characters-of-all-substrings-of-a-given-string"]}, {"contest_title": "\u7b2c 84 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 84", "contest_title_slug": "weekly-contest-84", "contest_id": 6, "contest_start_time": 1526175000, "contest_duration": 5400, "user_num": 656, "question_slugs": ["flipping-an-image", "find-and-replace-in-string", "image-overlap", "sum-of-distances-in-tree"]}, {"contest_title": "\u7b2c 85 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 85", "contest_title_slug": "weekly-contest-85", "contest_id": 7, "contest_start_time": 1526779800, "contest_duration": 5400, "user_num": 467, "question_slugs": ["rectangle-overlap", "push-dominoes", "new-21-game", "similar-string-groups"]}, {"contest_title": "\u7b2c 86 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 86", "contest_title_slug": "weekly-contest-86", "contest_id": 8, "contest_start_time": 1527384600, "contest_duration": 5400, "user_num": 377, "question_slugs": ["magic-squares-in-grid", "keys-and-rooms", "split-array-into-fibonacci-sequence", "guess-the-word"]}, {"contest_title": "\u7b2c 87 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 87", "contest_title_slug": "weekly-contest-87", "contest_id": 9, "contest_start_time": 1527989400, "contest_duration": 5400, "user_num": 343, "question_slugs": ["backspace-string-compare", "longest-mountain-in-array", "hand-of-straights", "shortest-path-visiting-all-nodes"]}, {"contest_title": "\u7b2c 88 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 88", "contest_title_slug": "weekly-contest-88", "contest_id": 11, "contest_start_time": 1528594200, "contest_duration": 5400, "user_num": 404, "question_slugs": ["shifting-letters", "maximize-distance-to-closest-person", "loud-and-rich", "rectangle-area-ii"]}, {"contest_title": "\u7b2c 89 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 89", "contest_title_slug": "weekly-contest-89", "contest_id": 12, "contest_start_time": 1529199000, "contest_duration": 5400, "user_num": 491, "question_slugs": ["peak-index-in-a-mountain-array", "car-fleet", "exam-room", "k-similar-strings"]}, {"contest_title": "\u7b2c 90 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 90", "contest_title_slug": "weekly-contest-90", "contest_id": 13, "contest_start_time": 1529803800, "contest_duration": 5400, "user_num": 573, "question_slugs": ["buddy-strings", "score-of-parentheses", "mirror-reflection", "minimum-cost-to-hire-k-workers"]}, {"contest_title": "\u7b2c 91 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 91", "contest_title_slug": "weekly-contest-91", "contest_id": 14, "contest_start_time": 1530408600, "contest_duration": 5400, "user_num": 578, "question_slugs": ["lemonade-change", "all-nodes-distance-k-in-binary-tree", "score-after-flipping-matrix", "shortest-subarray-with-sum-at-least-k"]}, {"contest_title": "\u7b2c 92 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 92", "contest_title_slug": "weekly-contest-92", "contest_id": 15, "contest_start_time": 1531013400, "contest_duration": 5400, "user_num": 610, "question_slugs": ["transpose-matrix", "smallest-subtree-with-all-the-deepest-nodes", "prime-palindrome", "shortest-path-to-get-all-keys"]}, {"contest_title": "\u7b2c 93 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 93", "contest_title_slug": "weekly-contest-93", "contest_id": 16, "contest_start_time": 1531618200, "contest_duration": 5400, "user_num": 732, "question_slugs": ["binary-gap", "reordered-power-of-2", "advantage-shuffle", "minimum-number-of-refueling-stops"]}, {"contest_title": "\u7b2c 94 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 94", "contest_title_slug": "weekly-contest-94", "contest_id": 17, "contest_start_time": 1532223000, "contest_duration": 5400, "user_num": 733, "question_slugs": ["leaf-similar-trees", "walking-robot-simulation", "koko-eating-bananas", "length-of-longest-fibonacci-subsequence"]}, {"contest_title": "\u7b2c 95 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 95", "contest_title_slug": "weekly-contest-95", "contest_id": 18, "contest_start_time": 1532827800, "contest_duration": 5400, "user_num": 831, "question_slugs": ["middle-of-the-linked-list", "stone-game", "nth-magical-number", "profitable-schemes"]}, {"contest_title": "\u7b2c 96 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 96", "contest_title_slug": "weekly-contest-96", "contest_id": 19, "contest_start_time": 1533432600, "contest_duration": 5400, "user_num": 789, "question_slugs": ["projection-area-of-3d-shapes", "boats-to-save-people", "decoded-string-at-index", "reachable-nodes-in-subdivided-graph"]}, {"contest_title": "\u7b2c 97 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 97", "contest_title_slug": "weekly-contest-97", "contest_id": 20, "contest_start_time": 1534037400, "contest_duration": 5400, "user_num": 635, "question_slugs": ["uncommon-words-from-two-sentences", "spiral-matrix-iii", "possible-bipartition", "super-egg-drop"]}, {"contest_title": "\u7b2c 98 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 98", "contest_title_slug": "weekly-contest-98", "contest_id": 21, "contest_start_time": 1534642200, "contest_duration": 5400, "user_num": 670, "question_slugs": ["fair-candy-swap", "find-and-replace-pattern", "construct-binary-tree-from-preorder-and-postorder-traversal", "sum-of-subsequence-widths"]}, {"contest_title": "\u7b2c 99 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 99", "contest_title_slug": "weekly-contest-99", "contest_id": 22, "contest_start_time": 1535247000, "contest_duration": 5400, "user_num": 725, "question_slugs": ["surface-area-of-3d-shapes", "groups-of-special-equivalent-strings", "all-possible-full-binary-trees", "maximum-frequency-stack"]}, {"contest_title": "\u7b2c 100 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 100", "contest_title_slug": "weekly-contest-100", "contest_id": 23, "contest_start_time": 1535851800, "contest_duration": 5400, "user_num": 718, "question_slugs": ["monotonic-array", "increasing-order-search-tree", "bitwise-ors-of-subarrays", "orderly-queue"]}, {"contest_title": "\u7b2c 101 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 101", "contest_title_slug": "weekly-contest-101", "contest_id": 24, "contest_start_time": 1536456600, "contest_duration": 6300, "user_num": 854, "question_slugs": ["rle-iterator", "online-stock-span", "numbers-at-most-n-given-digit-set", "valid-permutations-for-di-sequence"]}, {"contest_title": "\u7b2c 102 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 102", "contest_title_slug": "weekly-contest-102", "contest_id": 25, "contest_start_time": 1537061400, "contest_duration": 5400, "user_num": 660, "question_slugs": ["sort-array-by-parity", "fruit-into-baskets", "sum-of-subarray-minimums", "super-palindromes"]}, {"contest_title": "\u7b2c 103 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 103", "contest_title_slug": "weekly-contest-103", "contest_id": 26, "contest_start_time": 1537666200, "contest_duration": 5400, "user_num": 575, "question_slugs": ["smallest-range-i", "snakes-and-ladders", "smallest-range-ii", "online-election"]}, {"contest_title": "\u7b2c 104 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 104", "contest_title_slug": "weekly-contest-104", "contest_id": 27, "contest_start_time": 1538271000, "contest_duration": 5400, "user_num": 354, "question_slugs": ["x-of-a-kind-in-a-deck-of-cards", "partition-array-into-disjoint-intervals", "word-subsets", "cat-and-mouse"]}, {"contest_title": "\u7b2c 105 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 105", "contest_title_slug": "weekly-contest-105", "contest_id": 28, "contest_start_time": 1538875800, "contest_duration": 5400, "user_num": 393, "question_slugs": ["reverse-only-letters", "maximum-sum-circular-subarray", "complete-binary-tree-inserter", "number-of-music-playlists"]}, {"contest_title": "\u7b2c 106 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 106", "contest_title_slug": "weekly-contest-106", "contest_id": 29, "contest_start_time": 1539480600, "contest_duration": 5400, "user_num": 369, "question_slugs": ["sort-array-by-parity-ii", "minimum-add-to-make-parentheses-valid", "3sum-with-multiplicity", "minimize-malware-spread"]}, {"contest_title": "\u7b2c 107 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 107", "contest_title_slug": "weekly-contest-107", "contest_id": 30, "contest_start_time": 1540085400, "contest_duration": 5400, "user_num": 504, "question_slugs": ["long-pressed-name", "flip-string-to-monotone-increasing", "three-equal-parts", "minimize-malware-spread-ii"]}, {"contest_title": "\u7b2c 108 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 108", "contest_title_slug": "weekly-contest-108", "contest_id": 31, "contest_start_time": 1540690200, "contest_duration": 5400, "user_num": 524, "question_slugs": ["unique-email-addresses", "binary-subarrays-with-sum", "minimum-falling-path-sum", "beautiful-array"]}, {"contest_title": "\u7b2c 109 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 109", "contest_title_slug": "weekly-contest-109", "contest_id": 32, "contest_start_time": 1541295000, "contest_duration": 5400, "user_num": 439, "question_slugs": ["number-of-recent-calls", "knight-dialer", "shortest-bridge", "stamping-the-sequence"]}, {"contest_title": "\u7b2c 110 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 110", "contest_title_slug": "weekly-contest-110", "contest_id": 33, "contest_start_time": 1541903400, "contest_duration": 5400, "user_num": 346, "question_slugs": ["reorder-data-in-log-files", "range-sum-of-bst", "minimum-area-rectangle", "distinct-subsequences-ii"]}, {"contest_title": "\u7b2c 111 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 111", "contest_title_slug": "weekly-contest-111", "contest_id": 34, "contest_start_time": 1542508200, "contest_duration": 5400, "user_num": 353, "question_slugs": ["valid-mountain-array", "delete-columns-to-make-sorted", "di-string-match", "find-the-shortest-superstring"]}, {"contest_title": "\u7b2c 112 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 112", "contest_title_slug": "weekly-contest-112", "contest_id": 35, "contest_start_time": 1543113000, "contest_duration": 5400, "user_num": 299, "question_slugs": ["minimum-increment-to-make-array-unique", "validate-stack-sequences", "most-stones-removed-with-same-row-or-column", "bag-of-tokens"]}, {"contest_title": "\u7b2c 113 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 113", "contest_title_slug": "weekly-contest-113", "contest_id": 36, "contest_start_time": 1543717800, "contest_duration": 5400, "user_num": 462, "question_slugs": ["largest-time-for-given-digits", "flip-equivalent-binary-trees", "reveal-cards-in-increasing-order", "largest-component-size-by-common-factor"]}, {"contest_title": "\u7b2c 114 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 114", "contest_title_slug": "weekly-contest-114", "contest_id": 37, "contest_start_time": 1544322600, "contest_duration": 5400, "user_num": 391, "question_slugs": ["verifying-an-alien-dictionary", "array-of-doubled-pairs", "delete-columns-to-make-sorted-ii", "tallest-billboard"]}, {"contest_title": "\u7b2c 115 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 115", "contest_title_slug": "weekly-contest-115", "contest_id": 38, "contest_start_time": 1544927400, "contest_duration": 5400, "user_num": 383, "question_slugs": ["prison-cells-after-n-days", "check-completeness-of-a-binary-tree", "regions-cut-by-slashes", "delete-columns-to-make-sorted-iii"]}, {"contest_title": "\u7b2c 116 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 116", "contest_title_slug": "weekly-contest-116", "contest_id": 39, "contest_start_time": 1545532200, "contest_duration": 5400, "user_num": 369, "question_slugs": ["n-repeated-element-in-size-2n-array", "maximum-width-ramp", "minimum-area-rectangle-ii", "least-operators-to-express-number"]}, {"contest_title": "\u7b2c 117 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 117", "contest_title_slug": "weekly-contest-117", "contest_id": 41, "contest_start_time": 1546137000, "contest_duration": 5400, "user_num": 657, "question_slugs": ["univalued-binary-tree", "numbers-with-same-consecutive-differences", "vowel-spellchecker", "binary-tree-cameras"]}, {"contest_title": "\u7b2c 118 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 118", "contest_title_slug": "weekly-contest-118", "contest_id": 42, "contest_start_time": 1546741800, "contest_duration": 5400, "user_num": 383, "question_slugs": ["powerful-integers", "pancake-sorting", "flip-binary-tree-to-match-preorder-traversal", "equal-rational-numbers"]}, {"contest_title": "\u7b2c 119 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 119", "contest_title_slug": "weekly-contest-119", "contest_id": 43, "contest_start_time": 1547346600, "contest_duration": 5400, "user_num": 513, "question_slugs": ["k-closest-points-to-origin", "largest-perimeter-triangle", "subarray-sums-divisible-by-k", "odd-even-jump"]}, {"contest_title": "\u7b2c 120 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 120", "contest_title_slug": "weekly-contest-120", "contest_id": 44, "contest_start_time": 1547951400, "contest_duration": 5400, "user_num": 382, "question_slugs": ["squares-of-a-sorted-array", "longest-turbulent-subarray", "distribute-coins-in-binary-tree", "unique-paths-iii"]}, {"contest_title": "\u7b2c 121 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 121", "contest_title_slug": "weekly-contest-121", "contest_id": 45, "contest_start_time": 1548556200, "contest_duration": 5400, "user_num": 384, "question_slugs": ["string-without-aaa-or-bbb", "time-based-key-value-store", "minimum-cost-for-tickets", "triples-with-bitwise-and-equal-to-zero"]}, {"contest_title": "\u7b2c 122 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 122", "contest_title_slug": "weekly-contest-122", "contest_id": 46, "contest_start_time": 1549161000, "contest_duration": 5400, "user_num": 280, "question_slugs": ["sum-of-even-numbers-after-queries", "smallest-string-starting-from-leaf", "interval-list-intersections", "vertical-order-traversal-of-a-binary-tree"]}, {"contest_title": "\u7b2c 123 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 123", "contest_title_slug": "weekly-contest-123", "contest_id": 47, "contest_start_time": 1549765800, "contest_duration": 5400, "user_num": 247, "question_slugs": ["add-to-array-form-of-integer", "satisfiability-of-equality-equations", "broken-calculator", "subarrays-with-k-different-integers"]}, {"contest_title": "\u7b2c 124 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 124", "contest_title_slug": "weekly-contest-124", "contest_id": 48, "contest_start_time": 1550370600, "contest_duration": 5400, "user_num": 417, "question_slugs": ["cousins-in-binary-tree", "rotting-oranges", "minimum-number-of-k-consecutive-bit-flips", "number-of-squareful-arrays"]}, {"contest_title": "\u7b2c 125 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 125", "contest_title_slug": "weekly-contest-125", "contest_id": 49, "contest_start_time": 1550975400, "contest_duration": 5400, "user_num": 469, "question_slugs": ["find-the-town-judge", "available-captures-for-rook", "maximum-binary-tree-ii", "grid-illumination"]}, {"contest_title": "\u7b2c 126 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 126", "contest_title_slug": "weekly-contest-126", "contest_id": 50, "contest_start_time": 1551580200, "contest_duration": 5400, "user_num": 591, "question_slugs": ["find-common-characters", "check-if-word-is-valid-after-substitutions", "max-consecutive-ones-iii", "minimum-cost-to-merge-stones"]}, {"contest_title": "\u7b2c 127 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 127", "contest_title_slug": "weekly-contest-127", "contest_id": 52, "contest_start_time": 1552185000, "contest_duration": 5400, "user_num": 664, "question_slugs": ["maximize-sum-of-array-after-k-negations", "clumsy-factorial", "minimum-domino-rotations-for-equal-row", "construct-binary-search-tree-from-preorder-traversal"]}, {"contest_title": "\u7b2c 128 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 128", "contest_title_slug": "weekly-contest-128", "contest_id": 53, "contest_start_time": 1552789800, "contest_duration": 5400, "user_num": 1251, "question_slugs": ["complement-of-base-10-integer", "pairs-of-songs-with-total-durations-divisible-by-60", "capacity-to-ship-packages-within-d-days", "numbers-with-repeated-digits"]}, {"contest_title": "\u7b2c 129 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 129", "contest_title_slug": "weekly-contest-129", "contest_id": 54, "contest_start_time": 1553391000, "contest_duration": 5400, "user_num": 759, "question_slugs": ["partition-array-into-three-parts-with-equal-sum", "smallest-integer-divisible-by-k", "best-sightseeing-pair", "binary-string-with-substrings-representing-1-to-n"]}, {"contest_title": "\u7b2c 130 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 130", "contest_title_slug": "weekly-contest-130", "contest_id": 55, "contest_start_time": 1553999400, "contest_duration": 5400, "user_num": 1294, "question_slugs": ["binary-prefix-divisible-by-5", "convert-to-base-2", "next-greater-node-in-linked-list", "number-of-enclaves"]}, {"contest_title": "\u7b2c 131 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 131", "contest_title_slug": "weekly-contest-131", "contest_id": 56, "contest_start_time": 1554604200, "contest_duration": 5400, "user_num": 918, "question_slugs": ["remove-outermost-parentheses", "sum-of-root-to-leaf-binary-numbers", "camelcase-matching", "video-stitching"]}, {"contest_title": "\u7b2c 132 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 132", "contest_title_slug": "weekly-contest-132", "contest_id": 57, "contest_start_time": 1555209000, "contest_duration": 5400, "user_num": 1050, "question_slugs": ["divisor-game", "maximum-difference-between-node-and-ancestor", "longest-arithmetic-subsequence", "recover-a-tree-from-preorder-traversal"]}, {"contest_title": "\u7b2c 133 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 133", "contest_title_slug": "weekly-contest-133", "contest_id": 59, "contest_start_time": 1555813800, "contest_duration": 5400, "user_num": 999, "question_slugs": ["two-city-scheduling", "matrix-cells-in-distance-order", "maximum-sum-of-two-non-overlapping-subarrays", "stream-of-characters"]}, {"contest_title": "\u7b2c 134 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 134", "contest_title_slug": "weekly-contest-134", "contest_id": 64, "contest_start_time": 1556418600, "contest_duration": 5400, "user_num": 728, "question_slugs": ["moving-stones-until-consecutive", "coloring-a-border", "uncrossed-lines", "escape-a-large-maze"]}, {"contest_title": "\u7b2c 135 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 135", "contest_title_slug": "weekly-contest-135", "contest_id": 65, "contest_start_time": 1557023400, "contest_duration": 5400, "user_num": 549, "question_slugs": ["valid-boomerang", "binary-search-tree-to-greater-sum-tree", "minimum-score-triangulation-of-polygon", "moving-stones-until-consecutive-ii"]}, {"contest_title": "\u7b2c 136 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 136", "contest_title_slug": "weekly-contest-136", "contest_id": 66, "contest_start_time": 1557628200, "contest_duration": 5400, "user_num": 790, "question_slugs": ["robot-bounded-in-circle", "flower-planting-with-no-adjacent", "partition-array-for-maximum-sum", "longest-duplicate-substring"]}, {"contest_title": "\u7b2c 137 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 137", "contest_title_slug": "weekly-contest-137", "contest_id": 67, "contest_start_time": 1558233000, "contest_duration": 5400, "user_num": 766, "question_slugs": ["last-stone-weight", "remove-all-adjacent-duplicates-in-string", "longest-string-chain", "last-stone-weight-ii"]}, {"contest_title": "\u7b2c 138 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 138", "contest_title_slug": "weekly-contest-138", "contest_id": 68, "contest_start_time": 1558837800, "contest_duration": 5400, "user_num": 752, "question_slugs": ["height-checker", "grumpy-bookstore-owner", "previous-permutation-with-one-swap", "distant-barcodes"]}, {"contest_title": "\u7b2c 139 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 139", "contest_title_slug": "weekly-contest-139", "contest_id": 69, "contest_start_time": 1559442600, "contest_duration": 5400, "user_num": 785, "question_slugs": ["greatest-common-divisor-of-strings", "flip-columns-for-maximum-number-of-equal-rows", "adding-two-negabinary-numbers", "number-of-submatrices-that-sum-to-target"]}, {"contest_title": "\u7b2c 140 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 140", "contest_title_slug": "weekly-contest-140", "contest_id": 71, "contest_start_time": 1560047400, "contest_duration": 5400, "user_num": 660, "question_slugs": ["occurrences-after-bigram", "letter-tile-possibilities", "insufficient-nodes-in-root-to-leaf-paths", "smallest-subsequence-of-distinct-characters"]}, {"contest_title": "\u7b2c 141 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 141", "contest_title_slug": "weekly-contest-141", "contest_id": 72, "contest_start_time": 1560652200, "contest_duration": 5400, "user_num": 763, "question_slugs": ["duplicate-zeros", "largest-values-from-labels", "shortest-path-in-binary-matrix", "shortest-common-supersequence"]}, {"contest_title": "\u7b2c 142 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 142", "contest_title_slug": "weekly-contest-142", "contest_id": 74, "contest_start_time": 1561257000, "contest_duration": 5400, "user_num": 801, "question_slugs": ["statistics-from-a-large-sample", "car-pooling", "find-in-mountain-array", "brace-expansion-ii"]}, {"contest_title": "\u7b2c 143 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 143", "contest_title_slug": "weekly-contest-143", "contest_id": 84, "contest_start_time": 1561861800, "contest_duration": 5400, "user_num": 803, "question_slugs": ["distribute-candies-to-people", "path-in-zigzag-labelled-binary-tree", "filling-bookcase-shelves", "parsing-a-boolean-expression"]}, {"contest_title": "\u7b2c 144 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 144", "contest_title_slug": "weekly-contest-144", "contest_id": 86, "contest_start_time": 1562466600, "contest_duration": 5400, "user_num": 777, "question_slugs": ["defanging-an-ip-address", "corporate-flight-bookings", "delete-nodes-and-return-forest", "maximum-nesting-depth-of-two-valid-parentheses-strings"]}, {"contest_title": "\u7b2c 145 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 145", "contest_title_slug": "weekly-contest-145", "contest_id": 87, "contest_start_time": 1563071400, "contest_duration": 5400, "user_num": 1114, "question_slugs": ["relative-sort-array", "lowest-common-ancestor-of-deepest-leaves", "longest-well-performing-interval", "smallest-sufficient-team"]}, {"contest_title": "\u7b2c 146 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 146", "contest_title_slug": "weekly-contest-146", "contest_id": 89, "contest_start_time": 1563676200, "contest_duration": 5400, "user_num": 1189, "question_slugs": ["number-of-equivalent-domino-pairs", "shortest-path-with-alternating-colors", "minimum-cost-tree-from-leaf-values", "maximum-of-absolute-value-expression"]}, {"contest_title": "\u7b2c 147 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 147", "contest_title_slug": "weekly-contest-147", "contest_id": 90, "contest_start_time": 1564281000, "contest_duration": 5400, "user_num": 1132, "question_slugs": ["n-th-tribonacci-number", "alphabet-board-path", "largest-1-bordered-square", "stone-game-ii"]}, {"contest_title": "\u7b2c 148 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 148", "contest_title_slug": "weekly-contest-148", "contest_id": 93, "contest_start_time": 1564885800, "contest_duration": 5400, "user_num": 1251, "question_slugs": ["decrease-elements-to-make-array-zigzag", "binary-tree-coloring-game", "snapshot-array", "longest-chunked-palindrome-decomposition"]}, {"contest_title": "\u7b2c 149 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 149", "contest_title_slug": "weekly-contest-149", "contest_id": 94, "contest_start_time": 1565490600, "contest_duration": 5400, "user_num": 1351, "question_slugs": ["day-of-the-year", "number-of-dice-rolls-with-target-sum", "swap-for-longest-repeated-character-substring", "online-majority-element-in-subarray"]}, {"contest_title": "\u7b2c 150 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 150", "contest_title_slug": "weekly-contest-150", "contest_id": 96, "contest_start_time": 1566095400, "contest_duration": 5400, "user_num": 1473, "question_slugs": ["find-words-that-can-be-formed-by-characters", "maximum-level-sum-of-a-binary-tree", "as-far-from-land-as-possible", "last-substring-in-lexicographical-order"]}, {"contest_title": "\u7b2c 151 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 151", "contest_title_slug": "weekly-contest-151", "contest_id": 98, "contest_start_time": 1566700200, "contest_duration": 5400, "user_num": 1341, "question_slugs": ["invalid-transactions", "compare-strings-by-frequency-of-the-smallest-character", "remove-zero-sum-consecutive-nodes-from-linked-list", "dinner-plate-stacks"]}, {"contest_title": "\u7b2c 152 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 152", "contest_title_slug": "weekly-contest-152", "contest_id": 100, "contest_start_time": 1567305000, "contest_duration": 5400, "user_num": 1367, "question_slugs": ["prime-arrangements", "diet-plan-performance", "can-make-palindrome-from-substring", "number-of-valid-words-for-each-puzzle"]}, {"contest_title": "\u7b2c 153 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 153", "contest_title_slug": "weekly-contest-153", "contest_id": 102, "contest_start_time": 1567909800, "contest_duration": 5400, "user_num": 1434, "question_slugs": ["distance-between-bus-stops", "day-of-the-week", "maximum-subarray-sum-with-one-deletion", "make-array-strictly-increasing"]}, {"contest_title": "\u7b2c 154 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 154", "contest_title_slug": "weekly-contest-154", "contest_id": 106, "contest_start_time": 1568514600, "contest_duration": 5400, "user_num": 1299, "question_slugs": ["maximum-number-of-balloons", "reverse-substrings-between-each-pair-of-parentheses", "k-concatenation-maximum-sum", "critical-connections-in-a-network"]}, {"contest_title": "\u7b2c 155 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 155", "contest_title_slug": "weekly-contest-155", "contest_id": 107, "contest_start_time": 1569119400, "contest_duration": 5400, "user_num": 1603, "question_slugs": ["minimum-absolute-difference", "ugly-number-iii", "smallest-string-with-swaps", "sort-items-by-groups-respecting-dependencies"]}, {"contest_title": "\u7b2c 156 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 156", "contest_title_slug": "weekly-contest-156", "contest_id": 113, "contest_start_time": 1569724200, "contest_duration": 5400, "user_num": 1433, "question_slugs": ["unique-number-of-occurrences", "get-equal-substrings-within-budget", "remove-all-adjacent-duplicates-in-string-ii", "minimum-moves-to-reach-target-with-rotations"]}, {"contest_title": "\u7b2c 157 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 157", "contest_title_slug": "weekly-contest-157", "contest_id": 114, "contest_start_time": 1570329000, "contest_duration": 5400, "user_num": 1217, "question_slugs": ["minimum-cost-to-move-chips-to-the-same-position", "longest-arithmetic-subsequence-of-given-difference", "path-with-maximum-gold", "count-vowels-permutation"]}, {"contest_title": "\u7b2c 158 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 158", "contest_title_slug": "weekly-contest-158", "contest_id": 116, "contest_start_time": 1570933800, "contest_duration": 5400, "user_num": 1716, "question_slugs": ["split-a-string-in-balanced-strings", "queens-that-can-attack-the-king", "dice-roll-simulation", "maximum-equal-frequency"]}, {"contest_title": "\u7b2c 159 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 159", "contest_title_slug": "weekly-contest-159", "contest_id": 117, "contest_start_time": 1571538600, "contest_duration": 5400, "user_num": 1634, "question_slugs": ["check-if-it-is-a-straight-line", "remove-sub-folders-from-the-filesystem", "replace-the-substring-for-balanced-string", "maximum-profit-in-job-scheduling"]}, {"contest_title": "\u7b2c 160 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 160", "contest_title_slug": "weekly-contest-160", "contest_id": 119, "contest_start_time": 1572143400, "contest_duration": 5400, "user_num": 1692, "question_slugs": ["find-positive-integer-solution-for-a-given-equation", "circular-permutation-in-binary-representation", "maximum-length-of-a-concatenated-string-with-unique-characters", "tiling-a-rectangle-with-the-fewest-squares"]}, {"contest_title": "\u7b2c 161 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 161", "contest_title_slug": "weekly-contest-161", "contest_id": 120, "contest_start_time": 1572748200, "contest_duration": 5400, "user_num": 1610, "question_slugs": ["minimum-swaps-to-make-strings-equal", "count-number-of-nice-subarrays", "minimum-remove-to-make-valid-parentheses", "check-if-it-is-a-good-array"]}, {"contest_title": "\u7b2c 162 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 162", "contest_title_slug": "weekly-contest-162", "contest_id": 122, "contest_start_time": 1573353000, "contest_duration": 5400, "user_num": 1569, "question_slugs": ["cells-with-odd-values-in-a-matrix", "reconstruct-a-2-row-binary-matrix", "number-of-closed-islands", "maximum-score-words-formed-by-letters"]}, {"contest_title": "\u7b2c 163 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 163", "contest_title_slug": "weekly-contest-163", "contest_id": 123, "contest_start_time": 1573957800, "contest_duration": 5400, "user_num": 1605, "question_slugs": ["shift-2d-grid", "find-elements-in-a-contaminated-binary-tree", "greatest-sum-divisible-by-three", "minimum-moves-to-move-a-box-to-their-target-location"]}, {"contest_title": "\u7b2c 164 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 164", "contest_title_slug": "weekly-contest-164", "contest_id": 125, "contest_start_time": 1574562600, "contest_duration": 5400, "user_num": 1676, "question_slugs": ["minimum-time-visiting-all-points", "count-servers-that-communicate", "search-suggestions-system", "number-of-ways-to-stay-in-the-same-place-after-some-steps"]}, {"contest_title": "\u7b2c 165 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 165", "contest_title_slug": "weekly-contest-165", "contest_id": 128, "contest_start_time": 1575167400, "contest_duration": 5400, "user_num": 1660, "question_slugs": ["find-winner-on-a-tic-tac-toe-game", "number-of-burgers-with-no-waste-of-ingredients", "count-square-submatrices-with-all-ones", "palindrome-partitioning-iii"]}, {"contest_title": "\u7b2c 166 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 166", "contest_title_slug": "weekly-contest-166", "contest_id": 130, "contest_start_time": 1575772200, "contest_duration": 5400, "user_num": 1676, "question_slugs": ["subtract-the-product-and-sum-of-digits-of-an-integer", "group-the-people-given-the-group-size-they-belong-to", "find-the-smallest-divisor-given-a-threshold", "minimum-number-of-flips-to-convert-binary-matrix-to-zero-matrix"]}, {"contest_title": "\u7b2c 167 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 167", "contest_title_slug": "weekly-contest-167", "contest_id": 131, "contest_start_time": 1576377000, "contest_duration": 5400, "user_num": 1537, "question_slugs": ["convert-binary-number-in-a-linked-list-to-integer", "sequential-digits", "maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold", "shortest-path-in-a-grid-with-obstacles-elimination"]}, {"contest_title": "\u7b2c 168 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 168", "contest_title_slug": "weekly-contest-168", "contest_id": 133, "contest_start_time": 1576981800, "contest_duration": 5400, "user_num": 1553, "question_slugs": ["find-numbers-with-even-number-of-digits", "divide-array-in-sets-of-k-consecutive-numbers", "maximum-number-of-occurrences-of-a-substring", "maximum-candies-you-can-get-from-boxes"]}, {"contest_title": "\u7b2c 169 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 169", "contest_title_slug": "weekly-contest-169", "contest_id": 134, "contest_start_time": 1577586600, "contest_duration": 5400, "user_num": 1568, "question_slugs": ["find-n-unique-integers-sum-up-to-zero", "all-elements-in-two-binary-search-trees", "jump-game-iii", "verbal-arithmetic-puzzle"]}, {"contest_title": "\u7b2c 170 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 170", "contest_title_slug": "weekly-contest-170", "contest_id": 136, "contest_start_time": 1578191400, "contest_duration": 5400, "user_num": 1649, "question_slugs": ["decrypt-string-from-alphabet-to-integer-mapping", "xor-queries-of-a-subarray", "get-watched-videos-by-your-friends", "minimum-insertion-steps-to-make-a-string-palindrome"]}, {"contest_title": "\u7b2c 171 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 171", "contest_title_slug": "weekly-contest-171", "contest_id": 137, "contest_start_time": 1578796200, "contest_duration": 5400, "user_num": 1708, "question_slugs": ["convert-integer-to-the-sum-of-two-no-zero-integers", "minimum-flips-to-make-a-or-b-equal-to-c", "number-of-operations-to-make-network-connected", "minimum-distance-to-type-a-word-using-two-fingers"]}, {"contest_title": "\u7b2c 172 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 172", "contest_title_slug": "weekly-contest-172", "contest_id": 139, "contest_start_time": 1579401000, "contest_duration": 5400, "user_num": 1415, "question_slugs": ["maximum-69-number", "print-words-vertically", "delete-leaves-with-a-given-value", "minimum-number-of-taps-to-open-to-water-a-garden"]}, {"contest_title": "\u7b2c 173 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 173", "contest_title_slug": "weekly-contest-173", "contest_id": 142, "contest_start_time": 1580005800, "contest_duration": 5400, "user_num": 1072, "question_slugs": ["remove-palindromic-subsequences", "filter-restaurants-by-vegan-friendly-price-and-distance", "find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance", "minimum-difficulty-of-a-job-schedule"]}, {"contest_title": "\u7b2c 174 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 174", "contest_title_slug": "weekly-contest-174", "contest_id": 144, "contest_start_time": 1580610600, "contest_duration": 5400, "user_num": 1660, "question_slugs": ["the-k-weakest-rows-in-a-matrix", "reduce-array-size-to-the-half", "maximum-product-of-splitted-binary-tree", "jump-game-v"]}, {"contest_title": "\u7b2c 175 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 175", "contest_title_slug": "weekly-contest-175", "contest_id": 145, "contest_start_time": 1581215400, "contest_duration": 5400, "user_num": 2048, "question_slugs": ["check-if-n-and-its-double-exist", "minimum-number-of-steps-to-make-two-strings-anagram", "tweet-counts-per-frequency", "maximum-students-taking-exam"]}, {"contest_title": "\u7b2c 176 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 176", "contest_title_slug": "weekly-contest-176", "contest_id": 147, "contest_start_time": 1581820200, "contest_duration": 5400, "user_num": 2410, "question_slugs": ["count-negative-numbers-in-a-sorted-matrix", "product-of-the-last-k-numbers", "maximum-number-of-events-that-can-be-attended", "construct-target-array-with-multiple-sums"]}, {"contest_title": "\u7b2c 177 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 177", "contest_title_slug": "weekly-contest-177", "contest_id": 148, "contest_start_time": 1582425000, "contest_duration": 5400, "user_num": 2986, "question_slugs": ["number-of-days-between-two-dates", "validate-binary-tree-nodes", "closest-divisors", "largest-multiple-of-three"]}, {"contest_title": "\u7b2c 178 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 178", "contest_title_slug": "weekly-contest-178", "contest_id": 154, "contest_start_time": 1583029800, "contest_duration": 5400, "user_num": 3305, "question_slugs": ["how-many-numbers-are-smaller-than-the-current-number", "rank-teams-by-votes", "linked-list-in-binary-tree", "minimum-cost-to-make-at-least-one-valid-path-in-a-grid"]}, {"contest_title": "\u7b2c 179 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 179", "contest_title_slug": "weekly-contest-179", "contest_id": 156, "contest_start_time": 1583634600, "contest_duration": 5400, "user_num": 3606, "question_slugs": ["generate-a-string-with-characters-that-have-odd-counts", "number-of-times-binary-string-is-prefix-aligned", "time-needed-to-inform-all-employees", "frog-position-after-t-seconds"]}, {"contest_title": "\u7b2c 180 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 180", "contest_title_slug": "weekly-contest-180", "contest_id": 160, "contest_start_time": 1584239400, "contest_duration": 5400, "user_num": 3715, "question_slugs": ["lucky-numbers-in-a-matrix", "design-a-stack-with-increment-operation", "balance-a-binary-search-tree", "maximum-performance-of-a-team"]}, {"contest_title": "\u7b2c 181 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 181", "contest_title_slug": "weekly-contest-181", "contest_id": 162, "contest_start_time": 1584844200, "contest_duration": 5400, "user_num": 4149, "question_slugs": ["create-target-array-in-the-given-order", "four-divisors", "check-if-there-is-a-valid-path-in-a-grid", "longest-happy-prefix"]}, {"contest_title": "\u7b2c 182 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 182", "contest_title_slug": "weekly-contest-182", "contest_id": 166, "contest_start_time": 1585449000, "contest_duration": 5400, "user_num": 3911, "question_slugs": ["find-lucky-integer-in-an-array", "count-number-of-teams", "design-underground-system", "find-all-good-strings"]}, {"contest_title": "\u7b2c 183 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 183", "contest_title_slug": "weekly-contest-183", "contest_id": 168, "contest_start_time": 1586053800, "contest_duration": 5400, "user_num": 3756, "question_slugs": ["minimum-subsequence-in-non-increasing-order", "number-of-steps-to-reduce-a-number-in-binary-representation-to-one", "longest-happy-string", "stone-game-iii"]}, {"contest_title": "\u7b2c 184 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 184", "contest_title_slug": "weekly-contest-184", "contest_id": 175, "contest_start_time": 1586658600, "contest_duration": 5400, "user_num": 3847, "question_slugs": ["string-matching-in-an-array", "queries-on-a-permutation-with-key", "html-entity-parser", "number-of-ways-to-paint-n-3-grid"]}, {"contest_title": "\u7b2c 185 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 185", "contest_title_slug": "weekly-contest-185", "contest_id": 177, "contest_start_time": 1587263400, "contest_duration": 5400, "user_num": 5004, "question_slugs": ["reformat-the-string", "display-table-of-food-orders-in-a-restaurant", "minimum-number-of-frogs-croaking", "build-array-where-you-can-find-the-maximum-exactly-k-comparisons"]}, {"contest_title": "\u7b2c 186 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 186", "contest_title_slug": "weekly-contest-186", "contest_id": 185, "contest_start_time": 1587868200, "contest_duration": 5400, "user_num": 3108, "question_slugs": ["maximum-score-after-splitting-a-string", "maximum-points-you-can-obtain-from-cards", "diagonal-traverse-ii", "constrained-subsequence-sum"]}, {"contest_title": "\u7b2c 187 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 187", "contest_title_slug": "weekly-contest-187", "contest_id": 191, "contest_start_time": 1588473000, "contest_duration": 5400, "user_num": 3109, "question_slugs": ["destination-city", "check-if-all-1s-are-at-least-length-k-places-away", "longest-continuous-subarray-with-absolute-diff-less-than-or-equal-to-limit", "find-the-kth-smallest-sum-of-a-matrix-with-sorted-rows"]}, {"contest_title": "\u7b2c 188 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 188", "contest_title_slug": "weekly-contest-188", "contest_id": 195, "contest_start_time": 1589077800, "contest_duration": 5400, "user_num": 3982, "question_slugs": ["build-an-array-with-stack-operations", "count-triplets-that-can-form-two-arrays-of-equal-xor", "minimum-time-to-collect-all-apples-in-a-tree", "number-of-ways-of-cutting-a-pizza"]}, {"contest_title": "\u7b2c 189 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 189", "contest_title_slug": "weekly-contest-189", "contest_id": 197, "contest_start_time": 1589682600, "contest_duration": 5400, "user_num": 3692, "question_slugs": ["number-of-students-doing-homework-at-a-given-time", "rearrange-words-in-a-sentence", "people-whose-list-of-favorite-companies-is-not-a-subset-of-another-list", "maximum-number-of-darts-inside-of-a-circular-dartboard"]}, {"contest_title": "\u7b2c 190 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 190", "contest_title_slug": "weekly-contest-190", "contest_id": 201, "contest_start_time": 1590287400, "contest_duration": 5400, "user_num": 3352, "question_slugs": ["check-if-a-word-occurs-as-a-prefix-of-any-word-in-a-sentence", "maximum-number-of-vowels-in-a-substring-of-given-length", "pseudo-palindromic-paths-in-a-binary-tree", "max-dot-product-of-two-subsequences"]}, {"contest_title": "\u7b2c 191 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 191", "contest_title_slug": "weekly-contest-191", "contest_id": 203, "contest_start_time": 1590892200, "contest_duration": 5400, "user_num": 3687, "question_slugs": ["maximum-product-of-two-elements-in-an-array", "maximum-area-of-a-piece-of-cake-after-horizontal-and-vertical-cuts", "reorder-routes-to-make-all-paths-lead-to-the-city-zero", "probability-of-a-two-boxes-having-the-same-number-of-distinct-balls"]}, {"contest_title": "\u7b2c 192 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 192", "contest_title_slug": "weekly-contest-192", "contest_id": 207, "contest_start_time": 1591497000, "contest_duration": 5400, "user_num": 3615, "question_slugs": ["shuffle-the-array", "the-k-strongest-values-in-an-array", "design-browser-history", "paint-house-iii"]}, {"contest_title": "\u7b2c 193 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 193", "contest_title_slug": "weekly-contest-193", "contest_id": 209, "contest_start_time": 1592101800, "contest_duration": 5400, "user_num": 3804, "question_slugs": ["running-sum-of-1d-array", "least-number-of-unique-integers-after-k-removals", "minimum-number-of-days-to-make-m-bouquets", "kth-ancestor-of-a-tree-node"]}, {"contest_title": "\u7b2c 194 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 194", "contest_title_slug": "weekly-contest-194", "contest_id": 213, "contest_start_time": 1592706600, "contest_duration": 5400, "user_num": 4378, "question_slugs": ["xor-operation-in-an-array", "making-file-names-unique", "avoid-flood-in-the-city", "find-critical-and-pseudo-critical-edges-in-minimum-spanning-tree"]}, {"contest_title": "\u7b2c 195 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 195", "contest_title_slug": "weekly-contest-195", "contest_id": 215, "contest_start_time": 1593311400, "contest_duration": 5400, "user_num": 3401, "question_slugs": ["path-crossing", "check-if-array-pairs-are-divisible-by-k", "number-of-subsequences-that-satisfy-the-given-sum-condition", "max-value-of-equation"]}, {"contest_title": "\u7b2c 196 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 196", "contest_title_slug": "weekly-contest-196", "contest_id": 219, "contest_start_time": 1593916200, "contest_duration": 5400, "user_num": 5507, "question_slugs": ["can-make-arithmetic-progression-from-sequence", "last-moment-before-all-ants-fall-out-of-a-plank", "count-submatrices-with-all-ones", "minimum-possible-integer-after-at-most-k-adjacent-swaps-on-digits"]}, {"contest_title": "\u7b2c 197 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 197", "contest_title_slug": "weekly-contest-197", "contest_id": 221, "contest_start_time": 1594521000, "contest_duration": 5400, "user_num": 5275, "question_slugs": ["number-of-good-pairs", "number-of-substrings-with-only-1s", "path-with-maximum-probability", "best-position-for-a-service-centre"]}, {"contest_title": "\u7b2c 198 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 198", "contest_title_slug": "weekly-contest-198", "contest_id": 226, "contest_start_time": 1595125800, "contest_duration": 5400, "user_num": 5780, "question_slugs": ["water-bottles", "number-of-nodes-in-the-sub-tree-with-the-same-label", "maximum-number-of-non-overlapping-substrings", "find-a-value-of-a-mysterious-function-closest-to-target"]}, {"contest_title": "\u7b2c 199 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 199", "contest_title_slug": "weekly-contest-199", "contest_id": 228, "contest_start_time": 1595730600, "contest_duration": 5400, "user_num": 5232, "question_slugs": ["shuffle-string", "minimum-suffix-flips", "number-of-good-leaf-nodes-pairs", "string-compression-ii"]}, {"contest_title": "\u7b2c 200 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 200", "contest_title_slug": "weekly-contest-200", "contest_id": 235, "contest_start_time": 1596335400, "contest_duration": 5400, "user_num": 5476, "question_slugs": ["count-good-triplets", "find-the-winner-of-an-array-game", "minimum-swaps-to-arrange-a-binary-grid", "get-the-maximum-score"]}, {"contest_title": "\u7b2c 201 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 201", "contest_title_slug": "weekly-contest-201", "contest_id": 238, "contest_start_time": 1596940200, "contest_duration": 5400, "user_num": 5615, "question_slugs": ["make-the-string-great", "find-kth-bit-in-nth-binary-string", "maximum-number-of-non-overlapping-subarrays-with-sum-equals-target", "minimum-cost-to-cut-a-stick"]}, {"contest_title": "\u7b2c 202 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 202", "contest_title_slug": "weekly-contest-202", "contest_id": 242, "contest_start_time": 1597545000, "contest_duration": 5400, "user_num": 4990, "question_slugs": ["three-consecutive-odds", "minimum-operations-to-make-array-equal", "magnetic-force-between-two-balls", "minimum-number-of-days-to-eat-n-oranges"]}, {"contest_title": "\u7b2c 203 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 203", "contest_title_slug": "weekly-contest-203", "contest_id": 244, "contest_start_time": 1598149800, "contest_duration": 5400, "user_num": 5285, "question_slugs": ["most-visited-sector-in-a-circular-track", "maximum-number-of-coins-you-can-get", "find-latest-group-of-size-m", "stone-game-v"]}, {"contest_title": "\u7b2c 204 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 204", "contest_title_slug": "weekly-contest-204", "contest_id": 257, "contest_start_time": 1598754600, "contest_duration": 5400, "user_num": 4487, "question_slugs": ["detect-pattern-of-length-m-repeated-k-or-more-times", "maximum-length-of-subarray-with-positive-product", "minimum-number-of-days-to-disconnect-island", "number-of-ways-to-reorder-array-to-get-same-bst"]}, {"contest_title": "\u7b2c 205 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 205", "contest_title_slug": "weekly-contest-205", "contest_id": 260, "contest_start_time": 1599359400, "contest_duration": 5400, "user_num": 4176, "question_slugs": ["replace-all-s-to-avoid-consecutive-repeating-characters", "number-of-ways-where-square-of-number-is-equal-to-product-of-two-numbers", "minimum-time-to-make-rope-colorful", "remove-max-number-of-edges-to-keep-graph-fully-traversable"]}, {"contest_title": "\u7b2c 206 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 206", "contest_title_slug": "weekly-contest-206", "contest_id": 267, "contest_start_time": 1599964200, "contest_duration": 5400, "user_num": 4493, "question_slugs": ["special-positions-in-a-binary-matrix", "count-unhappy-friends", "min-cost-to-connect-all-points", "check-if-string-is-transformable-with-substring-sort-operations"]}, {"contest_title": "\u7b2c 207 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 207", "contest_title_slug": "weekly-contest-207", "contest_id": 278, "contest_start_time": 1600569000, "contest_duration": 5400, "user_num": 4116, "question_slugs": ["rearrange-spaces-between-words", "split-a-string-into-the-max-number-of-unique-substrings", "maximum-non-negative-product-in-a-matrix", "minimum-cost-to-connect-two-groups-of-points"]}, {"contest_title": "\u7b2c 208 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 208", "contest_title_slug": "weekly-contest-208", "contest_id": 289, "contest_start_time": 1601173800, "contest_duration": 5400, "user_num": 3582, "question_slugs": ["crawler-log-folder", "maximum-profit-of-operating-a-centennial-wheel", "throne-inheritance", "maximum-number-of-achievable-transfer-requests"]}, {"contest_title": "\u7b2c 209 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 209", "contest_title_slug": "weekly-contest-209", "contest_id": 291, "contest_start_time": 1601778600, "contest_duration": 5400, "user_num": 4023, "question_slugs": ["special-array-with-x-elements-greater-than-or-equal-x", "even-odd-tree", "maximum-number-of-visible-points", "minimum-one-bit-operations-to-make-integers-zero"]}, {"contest_title": "\u7b2c 210 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 210", "contest_title_slug": "weekly-contest-210", "contest_id": 295, "contest_start_time": 1602383400, "contest_duration": 5400, "user_num": 4007, "question_slugs": ["maximum-nesting-depth-of-the-parentheses", "maximal-network-rank", "split-two-strings-to-make-palindrome", "count-subtrees-with-max-distance-between-cities"]}, {"contest_title": "\u7b2c 211 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 211", "contest_title_slug": "weekly-contest-211", "contest_id": 297, "contest_start_time": 1602988200, "contest_duration": 5400, "user_num": 4034, "question_slugs": ["largest-substring-between-two-equal-characters", "lexicographically-smallest-string-after-applying-operations", "best-team-with-no-conflicts", "graph-connectivity-with-threshold"]}, {"contest_title": "\u7b2c 212 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 212", "contest_title_slug": "weekly-contest-212", "contest_id": 301, "contest_start_time": 1603593000, "contest_duration": 5400, "user_num": 4227, "question_slugs": ["slowest-key", "arithmetic-subarrays", "path-with-minimum-effort", "rank-transform-of-a-matrix"]}, {"contest_title": "\u7b2c 213 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 213", "contest_title_slug": "weekly-contest-213", "contest_id": 303, "contest_start_time": 1604197800, "contest_duration": 5400, "user_num": 3827, "question_slugs": ["check-array-formation-through-concatenation", "count-sorted-vowel-strings", "furthest-building-you-can-reach", "kth-smallest-instructions"]}, {"contest_title": "\u7b2c 214 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 214", "contest_title_slug": "weekly-contest-214", "contest_id": 307, "contest_start_time": 1604802600, "contest_duration": 5400, "user_num": 3598, "question_slugs": ["get-maximum-in-generated-array", "minimum-deletions-to-make-character-frequencies-unique", "sell-diminishing-valued-colored-balls", "create-sorted-array-through-instructions"]}, {"contest_title": "\u7b2c 215 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 215", "contest_title_slug": "weekly-contest-215", "contest_id": 309, "contest_start_time": 1605407400, "contest_duration": 5400, "user_num": 4429, "question_slugs": ["design-an-ordered-stream", "determine-if-two-strings-are-close", "minimum-operations-to-reduce-x-to-zero", "maximize-grid-happiness"]}, {"contest_title": "\u7b2c 216 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 216", "contest_title_slug": "weekly-contest-216", "contest_id": 313, "contest_start_time": 1606012200, "contest_duration": 5400, "user_num": 3857, "question_slugs": ["check-if-two-string-arrays-are-equivalent", "smallest-string-with-a-given-numeric-value", "ways-to-make-a-fair-array", "minimum-initial-energy-to-finish-tasks"]}, {"contest_title": "\u7b2c 217 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 217", "contest_title_slug": "weekly-contest-217", "contest_id": 315, "contest_start_time": 1606617000, "contest_duration": 5400, "user_num": 3745, "question_slugs": ["richest-customer-wealth", "find-the-most-competitive-subsequence", "minimum-moves-to-make-array-complementary", "minimize-deviation-in-array"]}, {"contest_title": "\u7b2c 218 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 218", "contest_title_slug": "weekly-contest-218", "contest_id": 319, "contest_start_time": 1607221800, "contest_duration": 5400, "user_num": 3762, "question_slugs": ["goal-parser-interpretation", "max-number-of-k-sum-pairs", "concatenation-of-consecutive-binary-numbers", "minimum-incompatibility"]}, {"contest_title": "\u7b2c 219 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 219", "contest_title_slug": "weekly-contest-219", "contest_id": 322, "contest_start_time": 1607826600, "contest_duration": 5400, "user_num": 3710, "question_slugs": ["count-of-matches-in-tournament", "partitioning-into-minimum-number-of-deci-binary-numbers", "stone-game-vii", "maximum-height-by-stacking-cuboids"]}, {"contest_title": "\u7b2c 220 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 220", "contest_title_slug": "weekly-contest-220", "contest_id": 326, "contest_start_time": 1608431400, "contest_duration": 5400, "user_num": 3691, "question_slugs": ["reformat-phone-number", "maximum-erasure-value", "jump-game-vi", "checking-existence-of-edge-length-limited-paths"]}, {"contest_title": "\u7b2c 221 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 221", "contest_title_slug": "weekly-contest-221", "contest_id": 328, "contest_start_time": 1609036200, "contest_duration": 5400, "user_num": 3398, "question_slugs": ["determine-if-string-halves-are-alike", "maximum-number-of-eaten-apples", "where-will-the-ball-fall", "maximum-xor-with-an-element-from-array"]}, {"contest_title": "\u7b2c 222 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 222", "contest_title_slug": "weekly-contest-222", "contest_id": 332, "contest_start_time": 1609641000, "contest_duration": 5400, "user_num": 3119, "question_slugs": ["maximum-units-on-a-truck", "count-good-meals", "ways-to-split-array-into-three-subarrays", "minimum-operations-to-make-a-subsequence"]}, {"contest_title": "\u7b2c 223 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 223", "contest_title_slug": "weekly-contest-223", "contest_id": 334, "contest_start_time": 1610245800, "contest_duration": 5400, "user_num": 3872, "question_slugs": ["decode-xored-array", "swapping-nodes-in-a-linked-list", "minimize-hamming-distance-after-swap-operations", "find-minimum-time-to-finish-all-jobs"]}, {"contest_title": "\u7b2c 224 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 224", "contest_title_slug": "weekly-contest-224", "contest_id": 338, "contest_start_time": 1610850600, "contest_duration": 5400, "user_num": 3795, "question_slugs": ["number-of-rectangles-that-can-form-the-largest-square", "tuple-with-same-product", "largest-submatrix-with-rearrangements", "cat-and-mouse-ii"]}, {"contest_title": "\u7b2c 225 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 225", "contest_title_slug": "weekly-contest-225", "contest_id": 340, "contest_start_time": 1611455400, "contest_duration": 5400, "user_num": 3853, "question_slugs": ["latest-time-by-replacing-hidden-digits", "change-minimum-characters-to-satisfy-one-of-three-conditions", "find-kth-largest-xor-coordinate-value", "building-boxes"]}, {"contest_title": "\u7b2c 226 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 226", "contest_title_slug": "weekly-contest-226", "contest_id": 344, "contest_start_time": 1612060200, "contest_duration": 5400, "user_num": 4034, "question_slugs": ["maximum-number-of-balls-in-a-box", "restore-the-array-from-adjacent-pairs", "can-you-eat-your-favorite-candy-on-your-favorite-day", "palindrome-partitioning-iv"]}, {"contest_title": "\u7b2c 227 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 227", "contest_title_slug": "weekly-contest-227", "contest_id": 346, "contest_start_time": 1612665000, "contest_duration": 5400, "user_num": 3546, "question_slugs": ["check-if-array-is-sorted-and-rotated", "maximum-score-from-removing-stones", "largest-merge-of-two-strings", "closest-subsequence-sum"]}, {"contest_title": "\u7b2c 228 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 228", "contest_title_slug": "weekly-contest-228", "contest_id": 350, "contest_start_time": 1613269800, "contest_duration": 5400, "user_num": 2484, "question_slugs": ["minimum-changes-to-make-alternating-binary-string", "count-number-of-homogenous-substrings", "minimum-limit-of-balls-in-a-bag", "minimum-degree-of-a-connected-trio-in-a-graph"]}, {"contest_title": "\u7b2c 229 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 229", "contest_title_slug": "weekly-contest-229", "contest_id": 352, "contest_start_time": 1613874600, "contest_duration": 5400, "user_num": 3484, "question_slugs": ["merge-strings-alternately", "minimum-number-of-operations-to-move-all-balls-to-each-box", "maximum-score-from-performing-multiplication-operations", "maximize-palindrome-length-from-subsequences"]}, {"contest_title": "\u7b2c 230 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 230", "contest_title_slug": "weekly-contest-230", "contest_id": 356, "contest_start_time": 1614479400, "contest_duration": 5400, "user_num": 3728, "question_slugs": ["count-items-matching-a-rule", "closest-dessert-cost", "equal-sum-arrays-with-minimum-number-of-operations", "car-fleet-ii"]}, {"contest_title": "\u7b2c 231 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 231", "contest_title_slug": "weekly-contest-231", "contest_id": 358, "contest_start_time": 1615084200, "contest_duration": 5400, "user_num": 4668, "question_slugs": ["check-if-binary-string-has-at-most-one-segment-of-ones", "minimum-elements-to-add-to-form-a-given-sum", "number-of-restricted-paths-from-first-to-last-node", "make-the-xor-of-all-segments-equal-to-zero"]}, {"contest_title": "\u7b2c 232 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 232", "contest_title_slug": "weekly-contest-232", "contest_id": 363, "contest_start_time": 1615689000, "contest_duration": 5400, "user_num": 4802, "question_slugs": ["check-if-one-string-swap-can-make-strings-equal", "find-center-of-star-graph", "maximum-average-pass-ratio", "maximum-score-of-a-good-subarray"]}, {"contest_title": "\u7b2c 233 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 233", "contest_title_slug": "weekly-contest-233", "contest_id": 371, "contest_start_time": 1616293800, "contest_duration": 5400, "user_num": 5010, "question_slugs": ["maximum-ascending-subarray-sum", "number-of-orders-in-the-backlog", "maximum-value-at-a-given-index-in-a-bounded-array", "count-pairs-with-xor-in-a-range"]}, {"contest_title": "\u7b2c 234 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 234", "contest_title_slug": "weekly-contest-234", "contest_id": 375, "contest_start_time": 1616898600, "contest_duration": 5400, "user_num": 4998, "question_slugs": ["number-of-different-integers-in-a-string", "minimum-number-of-operations-to-reinitialize-a-permutation", "evaluate-the-bracket-pairs-of-a-string", "maximize-number-of-nice-divisors"]}, {"contest_title": "\u7b2c 235 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 235", "contest_title_slug": "weekly-contest-235", "contest_id": 377, "contest_start_time": 1617503400, "contest_duration": 5400, "user_num": 4494, "question_slugs": ["truncate-sentence", "finding-the-users-active-minutes", "minimum-absolute-sum-difference", "number-of-different-subsequences-gcds"]}, {"contest_title": "\u7b2c 236 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 236", "contest_title_slug": "weekly-contest-236", "contest_id": 391, "contest_start_time": 1618108200, "contest_duration": 5400, "user_num": 5113, "question_slugs": ["sign-of-the-product-of-an-array", "find-the-winner-of-the-circular-game", "minimum-sideway-jumps", "finding-mk-average"]}, {"contest_title": "\u7b2c 237 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 237", "contest_title_slug": "weekly-contest-237", "contest_id": 393, "contest_start_time": 1618713000, "contest_duration": 5400, "user_num": 4577, "question_slugs": ["check-if-the-sentence-is-pangram", "maximum-ice-cream-bars", "single-threaded-cpu", "find-xor-sum-of-all-pairs-bitwise-and"]}, {"contest_title": "\u7b2c 238 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 238", "contest_title_slug": "weekly-contest-238", "contest_id": 397, "contest_start_time": 1619317800, "contest_duration": 5400, "user_num": 3978, "question_slugs": ["sum-of-digits-in-base-k", "frequency-of-the-most-frequent-element", "longest-substring-of-all-vowels-in-order", "maximum-building-height"]}, {"contest_title": "\u7b2c 239 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 239", "contest_title_slug": "weekly-contest-239", "contest_id": 399, "contest_start_time": 1619922600, "contest_duration": 5400, "user_num": 3907, "question_slugs": ["minimum-distance-to-the-target-element", "splitting-a-string-into-descending-consecutive-values", "minimum-adjacent-swaps-to-reach-the-kth-smallest-number", "minimum-interval-to-include-each-query"]}, {"contest_title": "\u7b2c 240 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 240", "contest_title_slug": "weekly-contest-240", "contest_id": 403, "contest_start_time": 1620527400, "contest_duration": 5400, "user_num": 4307, "question_slugs": ["maximum-population-year", "maximum-distance-between-a-pair-of-values", "maximum-subarray-min-product", "largest-color-value-in-a-directed-graph"]}, {"contest_title": "\u7b2c 241 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 241", "contest_title_slug": "weekly-contest-241", "contest_id": 405, "contest_start_time": 1621132200, "contest_duration": 5400, "user_num": 4491, "question_slugs": ["sum-of-all-subset-xor-totals", "minimum-number-of-swaps-to-make-the-binary-string-alternating", "finding-pairs-with-a-certain-sum", "number-of-ways-to-rearrange-sticks-with-k-sticks-visible"]}, {"contest_title": "\u7b2c 242 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 242", "contest_title_slug": "weekly-contest-242", "contest_id": 409, "contest_start_time": 1621737000, "contest_duration": 5400, "user_num": 4306, "question_slugs": ["longer-contiguous-segments-of-ones-than-zeros", "minimum-speed-to-arrive-on-time", "jump-game-vii", "stone-game-viii"]}, {"contest_title": "\u7b2c 243 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 243", "contest_title_slug": "weekly-contest-243", "contest_id": 411, "contest_start_time": 1622341800, "contest_duration": 5400, "user_num": 4493, "question_slugs": ["check-if-word-equals-summation-of-two-words", "maximum-value-after-insertion", "process-tasks-using-servers", "minimum-skips-to-arrive-at-meeting-on-time"]}, {"contest_title": "\u7b2c 244 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 244", "contest_title_slug": "weekly-contest-244", "contest_id": 415, "contest_start_time": 1622946600, "contest_duration": 5400, "user_num": 4430, "question_slugs": ["determine-whether-matrix-can-be-obtained-by-rotation", "reduction-operations-to-make-the-array-elements-equal", "minimum-number-of-flips-to-make-the-binary-string-alternating", "minimum-space-wasted-from-packaging"]}, {"contest_title": "\u7b2c 245 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 245", "contest_title_slug": "weekly-contest-245", "contest_id": 417, "contest_start_time": 1623551400, "contest_duration": 5400, "user_num": 4271, "question_slugs": ["redistribute-characters-to-make-all-strings-equal", "maximum-number-of-removable-characters", "merge-triplets-to-form-target-triplet", "the-earliest-and-latest-rounds-where-players-compete"]}, {"contest_title": "\u7b2c 246 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 246", "contest_title_slug": "weekly-contest-246", "contest_id": 422, "contest_start_time": 1624156200, "contest_duration": 5400, "user_num": 4136, "question_slugs": ["largest-odd-number-in-string", "the-number-of-full-rounds-you-have-played", "count-sub-islands", "minimum-absolute-difference-queries"]}, {"contest_title": "\u7b2c 247 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 247", "contest_title_slug": "weekly-contest-247", "contest_id": 426, "contest_start_time": 1624761000, "contest_duration": 5400, "user_num": 3981, "question_slugs": ["maximum-product-difference-between-two-pairs", "cyclically-rotating-a-grid", "number-of-wonderful-substrings", "count-ways-to-build-rooms-in-an-ant-colony"]}, {"contest_title": "\u7b2c 248 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 248", "contest_title_slug": "weekly-contest-248", "contest_id": 430, "contest_start_time": 1625365800, "contest_duration": 5400, "user_num": 4451, "question_slugs": ["build-array-from-permutation", "eliminate-maximum-number-of-monsters", "count-good-numbers", "longest-common-subpath"]}, {"contest_title": "\u7b2c 249 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 249", "contest_title_slug": "weekly-contest-249", "contest_id": 432, "contest_start_time": 1625970600, "contest_duration": 5400, "user_num": 4335, "question_slugs": ["concatenation-of-array", "unique-length-3-palindromic-subsequences", "painting-a-grid-with-three-different-colors", "merge-bsts-to-create-single-bst"]}, {"contest_title": "\u7b2c 250 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 250", "contest_title_slug": "weekly-contest-250", "contest_id": 436, "contest_start_time": 1626575400, "contest_duration": 5400, "user_num": 4315, "question_slugs": ["maximum-number-of-words-you-can-type", "add-minimum-number-of-rungs", "maximum-number-of-points-with-cost", "maximum-genetic-difference-query"]}, {"contest_title": "\u7b2c 251 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 251", "contest_title_slug": "weekly-contest-251", "contest_id": 438, "contest_start_time": 1627180200, "contest_duration": 5400, "user_num": 4747, "question_slugs": ["sum-of-digits-of-string-after-convert", "largest-number-after-mutating-substring", "maximum-compatibility-score-sum", "delete-duplicate-folders-in-system"]}, {"contest_title": "\u7b2c 252 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 252", "contest_title_slug": "weekly-contest-252", "contest_id": 442, "contest_start_time": 1627785000, "contest_duration": 5400, "user_num": 4647, "question_slugs": ["three-divisors", "maximum-number-of-weeks-for-which-you-can-work", "minimum-garden-perimeter-to-collect-enough-apples", "count-number-of-special-subsequences"]}, {"contest_title": "\u7b2c 253 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 253", "contest_title_slug": "weekly-contest-253", "contest_id": 444, "contest_start_time": 1628389800, "contest_duration": 5400, "user_num": 4570, "question_slugs": ["check-if-string-is-a-prefix-of-array", "remove-stones-to-minimize-the-total", "minimum-number-of-swaps-to-make-the-string-balanced", "find-the-longest-valid-obstacle-course-at-each-position"]}, {"contest_title": "\u7b2c 254 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 254", "contest_title_slug": "weekly-contest-254", "contest_id": 449, "contest_start_time": 1628994600, "contest_duration": 5400, "user_num": 4349, "question_slugs": ["number-of-strings-that-appear-as-substrings-in-word", "array-with-elements-not-equal-to-average-of-neighbors", "minimum-non-zero-product-of-the-array-elements", "last-day-where-you-can-still-cross"]}, {"contest_title": "\u7b2c 255 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 255", "contest_title_slug": "weekly-contest-255", "contest_id": 457, "contest_start_time": 1629599400, "contest_duration": 5400, "user_num": 4333, "question_slugs": ["find-greatest-common-divisor-of-array", "find-unique-binary-string", "minimize-the-difference-between-target-and-chosen-elements", "find-array-given-subset-sums"]}, {"contest_title": "\u7b2c 256 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 256", "contest_title_slug": "weekly-contest-256", "contest_id": 462, "contest_start_time": 1630204200, "contest_duration": 5400, "user_num": 4136, "question_slugs": ["minimum-difference-between-highest-and-lowest-of-k-scores", "find-the-kth-largest-integer-in-the-array", "minimum-number-of-work-sessions-to-finish-the-tasks", "number-of-unique-good-subsequences"]}, {"contest_title": "\u7b2c 257 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 257", "contest_title_slug": "weekly-contest-257", "contest_id": 464, "contest_start_time": 1630809000, "contest_duration": 5400, "user_num": 4278, "question_slugs": ["count-special-quadruplets", "the-number-of-weak-characters-in-the-game", "first-day-where-you-have-been-in-all-the-rooms", "gcd-sort-of-an-array"]}, {"contest_title": "\u7b2c 258 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 258", "contest_title_slug": "weekly-contest-258", "contest_id": 468, "contest_start_time": 1631413800, "contest_duration": 5400, "user_num": 4519, "question_slugs": ["reverse-prefix-of-word", "number-of-pairs-of-interchangeable-rectangles", "maximum-product-of-the-length-of-two-palindromic-subsequences", "smallest-missing-genetic-value-in-each-subtree"]}, {"contest_title": "\u7b2c 259 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 259", "contest_title_slug": "weekly-contest-259", "contest_id": 474, "contest_start_time": 1632018600, "contest_duration": 5400, "user_num": 3775, "question_slugs": ["final-value-of-variable-after-performing-operations", "sum-of-beauty-in-the-array", "detect-squares", "longest-subsequence-repeated-k-times"]}, {"contest_title": "\u7b2c 260 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 260", "contest_title_slug": "weekly-contest-260", "contest_id": 478, "contest_start_time": 1632623400, "contest_duration": 5400, "user_num": 3654, "question_slugs": ["maximum-difference-between-increasing-elements", "grid-game", "check-if-word-can-be-placed-in-crossword", "the-score-of-students-solving-math-expression"]}, {"contest_title": "\u7b2c 261 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 261", "contest_title_slug": "weekly-contest-261", "contest_id": 481, "contest_start_time": 1633228200, "contest_duration": 5400, "user_num": 3368, "question_slugs": ["minimum-moves-to-convert-string", "find-missing-observations", "stone-game-ix", "smallest-k-length-subsequence-with-occurrences-of-a-letter"]}, {"contest_title": "\u7b2c 262 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 262", "contest_title_slug": "weekly-contest-262", "contest_id": 485, "contest_start_time": 1633833000, "contest_duration": 5400, "user_num": 4261, "question_slugs": ["two-out-of-three", "minimum-operations-to-make-a-uni-value-grid", "stock-price-fluctuation", "partition-array-into-two-arrays-to-minimize-sum-difference"]}, {"contest_title": "\u7b2c 263 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 263", "contest_title_slug": "weekly-contest-263", "contest_id": 487, "contest_start_time": 1634437800, "contest_duration": 5400, "user_num": 4572, "question_slugs": ["check-if-numbers-are-ascending-in-a-sentence", "simple-bank-system", "count-number-of-maximum-bitwise-or-subsets", "second-minimum-time-to-reach-destination"]}, {"contest_title": "\u7b2c 264 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 264", "contest_title_slug": "weekly-contest-264", "contest_id": 491, "contest_start_time": 1635042600, "contest_duration": 5400, "user_num": 4659, "question_slugs": ["number-of-valid-words-in-a-sentence", "next-greater-numerically-balanced-number", "count-nodes-with-the-highest-score", "parallel-courses-iii"]}, {"contest_title": "\u7b2c 265 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 265", "contest_title_slug": "weekly-contest-265", "contest_id": 493, "contest_start_time": 1635647400, "contest_duration": 5400, "user_num": 4182, "question_slugs": ["smallest-index-with-equal-value", "find-the-minimum-and-maximum-number-of-nodes-between-critical-points", "minimum-operations-to-convert-number", "check-if-an-original-string-exists-given-two-encoded-strings"]}, {"contest_title": "\u7b2c 266 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 266", "contest_title_slug": "weekly-contest-266", "contest_id": 498, "contest_start_time": 1636252200, "contest_duration": 5400, "user_num": 4385, "question_slugs": ["count-vowel-substrings-of-a-string", "vowels-of-all-substrings", "minimized-maximum-of-products-distributed-to-any-store", "maximum-path-quality-of-a-graph"]}, {"contest_title": "\u7b2c 267 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 267", "contest_title_slug": "weekly-contest-267", "contest_id": 500, "contest_start_time": 1636857000, "contest_duration": 5400, "user_num": 4365, "question_slugs": ["time-needed-to-buy-tickets", "reverse-nodes-in-even-length-groups", "decode-the-slanted-ciphertext", "process-restricted-friend-requests"]}, {"contest_title": "\u7b2c 268 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 268", "contest_title_slug": "weekly-contest-268", "contest_id": 504, "contest_start_time": 1637461800, "contest_duration": 5400, "user_num": 4398, "question_slugs": ["two-furthest-houses-with-different-colors", "watering-plants", "range-frequency-queries", "sum-of-k-mirror-numbers"]}, {"contest_title": "\u7b2c 269 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 269", "contest_title_slug": "weekly-contest-269", "contest_id": 506, "contest_start_time": 1638066600, "contest_duration": 5400, "user_num": 4293, "question_slugs": ["find-target-indices-after-sorting-array", "k-radius-subarray-averages", "removing-minimum-and-maximum-from-array", "find-all-people-with-secret"]}, {"contest_title": "\u7b2c 270 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 270", "contest_title_slug": "weekly-contest-270", "contest_id": 510, "contest_start_time": 1638671400, "contest_duration": 5400, "user_num": 4748, "question_slugs": ["finding-3-digit-even-numbers", "delete-the-middle-node-of-a-linked-list", "step-by-step-directions-from-a-binary-tree-node-to-another", "valid-arrangement-of-pairs"]}, {"contest_title": "\u7b2c 271 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 271", "contest_title_slug": "weekly-contest-271", "contest_id": 512, "contest_start_time": 1639276200, "contest_duration": 5400, "user_num": 4562, "question_slugs": ["rings-and-rods", "sum-of-subarray-ranges", "watering-plants-ii", "maximum-fruits-harvested-after-at-most-k-steps"]}, {"contest_title": "\u7b2c 272 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 272", "contest_title_slug": "weekly-contest-272", "contest_id": 516, "contest_start_time": 1639881000, "contest_duration": 5400, "user_num": 4698, "question_slugs": ["find-first-palindromic-string-in-the-array", "adding-spaces-to-a-string", "number-of-smooth-descent-periods-of-a-stock", "minimum-operations-to-make-the-array-k-increasing"]}, {"contest_title": "\u7b2c 273 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 273", "contest_title_slug": "weekly-contest-273", "contest_id": 518, "contest_start_time": 1640485800, "contest_duration": 5400, "user_num": 4368, "question_slugs": ["a-number-after-a-double-reversal", "execution-of-all-suffix-instructions-staying-in-a-grid", "intervals-between-identical-elements", "recover-the-original-array"]}, {"contest_title": "\u7b2c 274 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 274", "contest_title_slug": "weekly-contest-274", "contest_id": 522, "contest_start_time": 1641090600, "contest_duration": 5400, "user_num": 4109, "question_slugs": ["check-if-all-as-appears-before-all-bs", "number-of-laser-beams-in-a-bank", "destroying-asteroids", "maximum-employees-to-be-invited-to-a-meeting"]}, {"contest_title": "\u7b2c 275 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 275", "contest_title_slug": "weekly-contest-275", "contest_id": 524, "contest_start_time": 1641695400, "contest_duration": 5400, "user_num": 4787, "question_slugs": ["check-if-every-row-and-column-contains-all-numbers", "minimum-swaps-to-group-all-1s-together-ii", "count-words-obtained-after-adding-a-letter", "earliest-possible-day-of-full-bloom"]}, {"contest_title": "\u7b2c 276 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 276", "contest_title_slug": "weekly-contest-276", "contest_id": 528, "contest_start_time": 1642300200, "contest_duration": 5400, "user_num": 5244, "question_slugs": ["divide-a-string-into-groups-of-size-k", "minimum-moves-to-reach-target-score", "solving-questions-with-brainpower", "maximum-running-time-of-n-computers"]}, {"contest_title": "\u7b2c 277 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 277", "contest_title_slug": "weekly-contest-277", "contest_id": 530, "contest_start_time": 1642905000, "contest_duration": 5400, "user_num": 5060, "question_slugs": ["count-elements-with-strictly-smaller-and-greater-elements", "rearrange-array-elements-by-sign", "find-all-lonely-numbers-in-the-array", "maximum-good-people-based-on-statements"]}, {"contest_title": "\u7b2c 278 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 278", "contest_title_slug": "weekly-contest-278", "contest_id": 534, "contest_start_time": 1643509800, "contest_duration": 5400, "user_num": 4643, "question_slugs": ["keep-multiplying-found-values-by-two", "all-divisions-with-the-highest-score-of-a-binary-array", "find-substring-with-given-hash-value", "groups-of-strings"]}, {"contest_title": "\u7b2c 279 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 279", "contest_title_slug": "weekly-contest-279", "contest_id": 536, "contest_start_time": 1644114600, "contest_duration": 5400, "user_num": 4132, "question_slugs": ["sort-even-and-odd-indices-independently", "smallest-value-of-the-rearranged-number", "design-bitset", "minimum-time-to-remove-all-cars-containing-illegal-goods"]}, {"contest_title": "\u7b2c 280 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 280", "contest_title_slug": "weekly-contest-280", "contest_id": 540, "contest_start_time": 1644719400, "contest_duration": 5400, "user_num": 5834, "question_slugs": ["count-operations-to-obtain-zero", "minimum-operations-to-make-the-array-alternating", "removing-minimum-number-of-magic-beans", "maximum-and-sum-of-array"]}, {"contest_title": "\u7b2c 281 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 281", "contest_title_slug": "weekly-contest-281", "contest_id": 542, "contest_start_time": 1645324200, "contest_duration": 6000, "user_num": 6005, "question_slugs": ["count-integers-with-even-digit-sum", "merge-nodes-in-between-zeros", "construct-string-with-repeat-limit", "count-array-pairs-divisible-by-k"]}, {"contest_title": "\u7b2c 282 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 282", "contest_title_slug": "weekly-contest-282", "contest_id": 546, "contest_start_time": 1645929000, "contest_duration": 5400, "user_num": 7164, "question_slugs": ["counting-words-with-a-given-prefix", "minimum-number-of-steps-to-make-two-strings-anagram-ii", "minimum-time-to-complete-trips", "minimum-time-to-finish-the-race"]}, {"contest_title": "\u7b2c 283 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 283", "contest_title_slug": "weekly-contest-283", "contest_id": 551, "contest_start_time": 1646533800, "contest_duration": 5400, "user_num": 7817, "question_slugs": ["cells-in-a-range-on-an-excel-sheet", "append-k-integers-with-minimal-sum", "create-binary-tree-from-descriptions", "replace-non-coprime-numbers-in-array"]}, {"contest_title": "\u7b2c 284 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 284", "contest_title_slug": "weekly-contest-284", "contest_id": 555, "contest_start_time": 1647138600, "contest_duration": 5400, "user_num": 8483, "question_slugs": ["find-all-k-distant-indices-in-an-array", "count-artifacts-that-can-be-extracted", "maximize-the-topmost-element-after-k-moves", "minimum-weighted-subgraph-with-the-required-paths"]}, {"contest_title": "\u7b2c 285 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 285", "contest_title_slug": "weekly-contest-285", "contest_id": 558, "contest_start_time": 1647743400, "contest_duration": 5400, "user_num": 7501, "question_slugs": ["count-hills-and-valleys-in-an-array", "count-collisions-on-a-road", "maximum-points-in-an-archery-competition", "longest-substring-of-one-repeating-character"]}, {"contest_title": "\u7b2c 286 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 286", "contest_title_slug": "weekly-contest-286", "contest_id": 564, "contest_start_time": 1648348200, "contest_duration": 5400, "user_num": 7248, "question_slugs": ["find-the-difference-of-two-arrays", "minimum-deletions-to-make-array-beautiful", "find-palindrome-with-fixed-length", "maximum-value-of-k-coins-from-piles"]}, {"contest_title": "\u7b2c 287 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 287", "contest_title_slug": "weekly-contest-287", "contest_id": 569, "contest_start_time": 1648953000, "contest_duration": 5400, "user_num": 6811, "question_slugs": ["minimum-number-of-operations-to-convert-time", "find-players-with-zero-or-one-losses", "maximum-candies-allocated-to-k-children", "encrypt-and-decrypt-strings"]}, {"contest_title": "\u7b2c 288 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 288", "contest_title_slug": "weekly-contest-288", "contest_id": 573, "contest_start_time": 1649557800, "contest_duration": 5400, "user_num": 6926, "question_slugs": ["largest-number-after-digit-swaps-by-parity", "minimize-result-by-adding-parentheses-to-expression", "maximum-product-after-k-increments", "maximum-total-beauty-of-the-gardens"]}, {"contest_title": "\u7b2c 289 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 289", "contest_title_slug": "weekly-contest-289", "contest_id": 576, "contest_start_time": 1650162600, "contest_duration": 5400, "user_num": 7293, "question_slugs": ["calculate-digit-sum-of-a-string", "minimum-rounds-to-complete-all-tasks", "maximum-trailing-zeros-in-a-cornered-path", "longest-path-with-different-adjacent-characters"]}, {"contest_title": "\u7b2c 290 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 290", "contest_title_slug": "weekly-contest-290", "contest_id": 582, "contest_start_time": 1650767400, "contest_duration": 5400, "user_num": 6275, "question_slugs": ["intersection-of-multiple-arrays", "count-lattice-points-inside-a-circle", "count-number-of-rectangles-containing-each-point", "number-of-flowers-in-full-bloom"]}, {"contest_title": "\u7b2c 291 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 291", "contest_title_slug": "weekly-contest-291", "contest_id": 587, "contest_start_time": 1651372200, "contest_duration": 5400, "user_num": 6574, "question_slugs": ["remove-digit-from-number-to-maximize-result", "minimum-consecutive-cards-to-pick-up", "k-divisible-elements-subarrays", "total-appeal-of-a-string"]}, {"contest_title": "\u7b2c 292 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 292", "contest_title_slug": "weekly-contest-292", "contest_id": 591, "contest_start_time": 1651977000, "contest_duration": 5400, "user_num": 6884, "question_slugs": ["largest-3-same-digit-number-in-string", "count-nodes-equal-to-average-of-subtree", "count-number-of-texts", "check-if-there-is-a-valid-parentheses-string-path"]}, {"contest_title": "\u7b2c 293 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 293", "contest_title_slug": "weekly-contest-293", "contest_id": 593, "contest_start_time": 1652581800, "contest_duration": 5400, "user_num": 7357, "question_slugs": ["find-resultant-array-after-removing-anagrams", "maximum-consecutive-floors-without-special-floors", "largest-combination-with-bitwise-and-greater-than-zero", "count-integers-in-intervals"]}, {"contest_title": "\u7b2c 294 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 294", "contest_title_slug": "weekly-contest-294", "contest_id": 599, "contest_start_time": 1653186600, "contest_duration": 5400, "user_num": 6640, "question_slugs": ["percentage-of-letter-in-string", "maximum-bags-with-full-capacity-of-rocks", "minimum-lines-to-represent-a-line-chart", "sum-of-total-strength-of-wizards"]}, {"contest_title": "\u7b2c 295 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 295", "contest_title_slug": "weekly-contest-295", "contest_id": 605, "contest_start_time": 1653791400, "contest_duration": 5400, "user_num": 6447, "question_slugs": ["rearrange-characters-to-make-target-string", "apply-discount-to-prices", "steps-to-make-array-non-decreasing", "minimum-obstacle-removal-to-reach-corner"]}, {"contest_title": "\u7b2c 296 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 296", "contest_title_slug": "weekly-contest-296", "contest_id": 609, "contest_start_time": 1654396200, "contest_duration": 5400, "user_num": 5721, "question_slugs": ["min-max-game", "partition-array-such-that-maximum-difference-is-k", "replace-elements-in-an-array", "design-a-text-editor"]}, {"contest_title": "\u7b2c 297 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 297", "contest_title_slug": "weekly-contest-297", "contest_id": 611, "contest_start_time": 1655001000, "contest_duration": 5400, "user_num": 5915, "question_slugs": ["calculate-amount-paid-in-taxes", "minimum-path-cost-in-a-grid", "fair-distribution-of-cookies", "naming-a-company"]}, {"contest_title": "\u7b2c 298 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 298", "contest_title_slug": "weekly-contest-298", "contest_id": 615, "contest_start_time": 1655605800, "contest_duration": 5400, "user_num": 6228, "question_slugs": ["greatest-english-letter-in-upper-and-lower-case", "sum-of-numbers-with-units-digit-k", "longest-binary-subsequence-less-than-or-equal-to-k", "selling-pieces-of-wood"]}, {"contest_title": "\u7b2c 299 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 299", "contest_title_slug": "weekly-contest-299", "contest_id": 618, "contest_start_time": 1656210600, "contest_duration": 5400, "user_num": 6108, "question_slugs": ["check-if-matrix-is-x-matrix", "count-number-of-ways-to-place-houses", "maximum-score-of-spliced-array", "minimum-score-after-removals-on-a-tree"]}, {"contest_title": "\u7b2c 300 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 300", "contest_title_slug": "weekly-contest-300", "contest_id": 647, "contest_start_time": 1656815400, "contest_duration": 5400, "user_num": 6792, "question_slugs": ["decode-the-message", "spiral-matrix-iv", "number-of-people-aware-of-a-secret", "number-of-increasing-paths-in-a-grid"]}, {"contest_title": "\u7b2c 301 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 301", "contest_title_slug": "weekly-contest-301", "contest_id": 649, "contest_start_time": 1657420200, "contest_duration": 5400, "user_num": 7133, "question_slugs": ["minimum-amount-of-time-to-fill-cups", "smallest-number-in-infinite-set", "move-pieces-to-obtain-a-string", "count-the-number-of-ideal-arrays"]}, {"contest_title": "\u7b2c 302 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 302", "contest_title_slug": "weekly-contest-302", "contest_id": 653, "contest_start_time": 1658025000, "contest_duration": 5400, "user_num": 7092, "question_slugs": ["maximum-number-of-pairs-in-array", "max-sum-of-a-pair-with-equal-sum-of-digits", "query-kth-smallest-trimmed-number", "minimum-deletions-to-make-array-divisible"]}, {"contest_title": "\u7b2c 303 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 303", "contest_title_slug": "weekly-contest-303", "contest_id": 655, "contest_start_time": 1658629800, "contest_duration": 5400, "user_num": 7032, "question_slugs": ["first-letter-to-appear-twice", "equal-row-and-column-pairs", "design-a-food-rating-system", "number-of-excellent-pairs"]}, {"contest_title": "\u7b2c 304 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 304", "contest_title_slug": "weekly-contest-304", "contest_id": 659, "contest_start_time": 1659234600, "contest_duration": 5400, "user_num": 7372, "question_slugs": ["make-array-zero-by-subtracting-equal-amounts", "maximum-number-of-groups-entering-a-competition", "find-closest-node-to-given-two-nodes", "longest-cycle-in-a-graph"]}, {"contest_title": "\u7b2c 305 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 305", "contest_title_slug": "weekly-contest-305", "contest_id": 663, "contest_start_time": 1659839400, "contest_duration": 5400, "user_num": 7465, "question_slugs": ["number-of-arithmetic-triplets", "reachable-nodes-with-restrictions", "check-if-there-is-a-valid-partition-for-the-array", "longest-ideal-subsequence"]}, {"contest_title": "\u7b2c 306 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 306", "contest_title_slug": "weekly-contest-306", "contest_id": 669, "contest_start_time": 1660444200, "contest_duration": 5400, "user_num": 7500, "question_slugs": ["largest-local-values-in-a-matrix", "node-with-highest-edge-score", "construct-smallest-number-from-di-string", "count-special-integers"]}, {"contest_title": "\u7b2c 307 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 307", "contest_title_slug": "weekly-contest-307", "contest_id": 671, "contest_start_time": 1661049000, "contest_duration": 5400, "user_num": 7064, "question_slugs": ["minimum-hours-of-training-to-win-a-competition", "largest-palindromic-number", "amount-of-time-for-binary-tree-to-be-infected", "find-the-k-sum-of-an-array"]}, {"contest_title": "\u7b2c 308 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 308", "contest_title_slug": "weekly-contest-308", "contest_id": 689, "contest_start_time": 1661653800, "contest_duration": 5400, "user_num": 6394, "question_slugs": ["longest-subsequence-with-limited-sum", "removing-stars-from-a-string", "minimum-amount-of-time-to-collect-garbage", "build-a-matrix-with-conditions"]}, {"contest_title": "\u7b2c 309 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 309", "contest_title_slug": "weekly-contest-309", "contest_id": 693, "contest_start_time": 1662258600, "contest_duration": 5400, "user_num": 7972, "question_slugs": ["check-distances-between-same-letters", "number-of-ways-to-reach-a-position-after-exactly-k-steps", "longest-nice-subarray", "meeting-rooms-iii"]}, {"contest_title": "\u7b2c 310 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 310", "contest_title_slug": "weekly-contest-310", "contest_id": 704, "contest_start_time": 1662863400, "contest_duration": 5400, "user_num": 6081, "question_slugs": ["most-frequent-even-element", "optimal-partition-of-string", "divide-intervals-into-minimum-number-of-groups", "longest-increasing-subsequence-ii"]}, {"contest_title": "\u7b2c 311 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 311", "contest_title_slug": "weekly-contest-311", "contest_id": 741, "contest_start_time": 1663468200, "contest_duration": 5400, "user_num": 6710, "question_slugs": ["smallest-even-multiple", "length-of-the-longest-alphabetical-continuous-substring", "reverse-odd-levels-of-binary-tree", "sum-of-prefix-scores-of-strings"]}, {"contest_title": "\u7b2c 312 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 312", "contest_title_slug": "weekly-contest-312", "contest_id": 746, "contest_start_time": 1664073000, "contest_duration": 5400, "user_num": 6638, "question_slugs": ["sort-the-people", "longest-subarray-with-maximum-bitwise-and", "find-all-good-indices", "number-of-good-paths"]}, {"contest_title": "\u7b2c 313 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 313", "contest_title_slug": "weekly-contest-313", "contest_id": 750, "contest_start_time": 1664677800, "contest_duration": 5400, "user_num": 5445, "question_slugs": ["number-of-common-factors", "maximum-sum-of-an-hourglass", "minimize-xor", "maximum-deletions-on-a-string"]}, {"contest_title": "\u7b2c 314 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 314", "contest_title_slug": "weekly-contest-314", "contest_id": 756, "contest_start_time": 1665282600, "contest_duration": 5400, "user_num": 4838, "question_slugs": ["the-employee-that-worked-on-the-longest-task", "find-the-original-array-of-prefix-xor", "using-a-robot-to-print-the-lexicographically-smallest-string", "paths-in-matrix-whose-sum-is-divisible-by-k"]}, {"contest_title": "\u7b2c 315 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 315", "contest_title_slug": "weekly-contest-315", "contest_id": 759, "contest_start_time": 1665887400, "contest_duration": 5400, "user_num": 6490, "question_slugs": ["largest-positive-integer-that-exists-with-its-negative", "count-number-of-distinct-integers-after-reverse-operations", "sum-of-number-and-its-reverse", "count-subarrays-with-fixed-bounds"]}, {"contest_title": "\u7b2c 316 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 316", "contest_title_slug": "weekly-contest-316", "contest_id": 764, "contest_start_time": 1666492200, "contest_duration": 5400, "user_num": 6387, "question_slugs": ["determine-if-two-events-have-conflict", "number-of-subarrays-with-gcd-equal-to-k", "minimum-cost-to-make-array-equal", "minimum-number-of-operations-to-make-arrays-similar"]}, {"contest_title": "\u7b2c 317 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 317", "contest_title_slug": "weekly-contest-317", "contest_id": 767, "contest_start_time": 1667097000, "contest_duration": 5400, "user_num": 5660, "question_slugs": ["average-value-of-even-numbers-that-are-divisible-by-three", "most-popular-video-creator", "minimum-addition-to-make-integer-beautiful", "height-of-binary-tree-after-subtree-removal-queries"]}, {"contest_title": "\u7b2c 318 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 318", "contest_title_slug": "weekly-contest-318", "contest_id": 771, "contest_start_time": 1667701800, "contest_duration": 5400, "user_num": 5670, "question_slugs": ["apply-operations-to-an-array", "maximum-sum-of-distinct-subarrays-with-length-k", "total-cost-to-hire-k-workers", "minimum-total-distance-traveled"]}, {"contest_title": "\u7b2c 319 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 319", "contest_title_slug": "weekly-contest-319", "contest_id": 773, "contest_start_time": 1668306600, "contest_duration": 5400, "user_num": 6175, "question_slugs": ["convert-the-temperature", "number-of-subarrays-with-lcm-equal-to-k", "minimum-number-of-operations-to-sort-a-binary-tree-by-level", "maximum-number-of-non-overlapping-palindrome-substrings"]}, {"contest_title": "\u7b2c 320 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 320", "contest_title_slug": "weekly-contest-320", "contest_id": 777, "contest_start_time": 1668911400, "contest_duration": 5400, "user_num": 5678, "question_slugs": ["number-of-unequal-triplets-in-array", "closest-nodes-queries-in-a-binary-search-tree", "minimum-fuel-cost-to-report-to-the-capital", "number-of-beautiful-partitions"]}, {"contest_title": "\u7b2c 321 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 321", "contest_title_slug": "weekly-contest-321", "contest_id": 779, "contest_start_time": 1669516200, "contest_duration": 5400, "user_num": 5115, "question_slugs": ["find-the-pivot-integer", "append-characters-to-string-to-make-subsequence", "remove-nodes-from-linked-list", "count-subarrays-with-median-k"]}, {"contest_title": "\u7b2c 322 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 322", "contest_title_slug": "weekly-contest-322", "contest_id": 783, "contest_start_time": 1670121000, "contest_duration": 5400, "user_num": 5085, "question_slugs": ["circular-sentence", "divide-players-into-teams-of-equal-skill", "minimum-score-of-a-path-between-two-cities", "divide-nodes-into-the-maximum-number-of-groups"]}, {"contest_title": "\u7b2c 323 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 323", "contest_title_slug": "weekly-contest-323", "contest_id": 785, "contest_start_time": 1670725800, "contest_duration": 5400, "user_num": 4671, "question_slugs": ["delete-greatest-value-in-each-row", "longest-square-streak-in-an-array", "design-memory-allocator", "maximum-number-of-points-from-grid-queries"]}, {"contest_title": "\u7b2c 324 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 324", "contest_title_slug": "weekly-contest-324", "contest_id": 790, "contest_start_time": 1671330600, "contest_duration": 5400, "user_num": 4167, "question_slugs": ["count-pairs-of-similar-strings", "smallest-value-after-replacing-with-sum-of-prime-factors", "add-edges-to-make-degrees-of-all-nodes-even", "cycle-length-queries-in-a-tree"]}, {"contest_title": "\u7b2c 325 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 325", "contest_title_slug": "weekly-contest-325", "contest_id": 795, "contest_start_time": 1671935400, "contest_duration": 5400, "user_num": 3530, "question_slugs": ["shortest-distance-to-target-string-in-a-circular-array", "take-k-of-each-character-from-left-and-right", "maximum-tastiness-of-candy-basket", "number-of-great-partitions"]}, {"contest_title": "\u7b2c 326 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 326", "contest_title_slug": "weekly-contest-326", "contest_id": 799, "contest_start_time": 1672540200, "contest_duration": 5400, "user_num": 3873, "question_slugs": ["count-the-digits-that-divide-a-number", "distinct-prime-factors-of-product-of-array", "partition-string-into-substrings-with-values-at-most-k", "closest-prime-numbers-in-range"]}, {"contest_title": "\u7b2c 327 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 327", "contest_title_slug": "weekly-contest-327", "contest_id": 801, "contest_start_time": 1673145000, "contest_duration": 5400, "user_num": 4518, "question_slugs": ["maximum-count-of-positive-integer-and-negative-integer", "maximal-score-after-applying-k-operations", "make-number-of-distinct-characters-equal", "time-to-cross-a-bridge"]}, {"contest_title": "\u7b2c 328 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 328", "contest_title_slug": "weekly-contest-328", "contest_id": 805, "contest_start_time": 1673749800, "contest_duration": 5400, "user_num": 4776, "question_slugs": ["difference-between-element-sum-and-digit-sum-of-an-array", "increment-submatrices-by-one", "count-the-number-of-good-subarrays", "difference-between-maximum-and-minimum-price-sum"]}, {"contest_title": "\u7b2c 329 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 329", "contest_title_slug": "weekly-contest-329", "contest_id": 807, "contest_start_time": 1674354600, "contest_duration": 5400, "user_num": 2591, "question_slugs": ["alternating-digit-sum", "sort-the-students-by-their-kth-score", "apply-bitwise-operations-to-make-strings-equal", "minimum-cost-to-split-an-array"]}, {"contest_title": "\u7b2c 330 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 330", "contest_title_slug": "weekly-contest-330", "contest_id": 811, "contest_start_time": 1674959400, "contest_duration": 5400, "user_num": 3399, "question_slugs": ["count-distinct-numbers-on-board", "count-collisions-of-monkeys-on-a-polygon", "put-marbles-in-bags", "count-increasing-quadruplets"]}, {"contest_title": "\u7b2c 331 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 331", "contest_title_slug": "weekly-contest-331", "contest_id": 813, "contest_start_time": 1675564200, "contest_duration": 5400, "user_num": 4256, "question_slugs": ["take-gifts-from-the-richest-pile", "count-vowel-strings-in-ranges", "house-robber-iv", "rearranging-fruits"]}, {"contest_title": "\u7b2c 332 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 332", "contest_title_slug": "weekly-contest-332", "contest_id": 817, "contest_start_time": 1676169000, "contest_duration": 5400, "user_num": 4547, "question_slugs": ["find-the-array-concatenation-value", "count-the-number-of-fair-pairs", "substring-xor-queries", "subsequence-with-the-minimum-score"]}, {"contest_title": "\u7b2c 333 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 333", "contest_title_slug": "weekly-contest-333", "contest_id": 819, "contest_start_time": 1676773800, "contest_duration": 5400, "user_num": 4969, "question_slugs": ["merge-two-2d-arrays-by-summing-values", "minimum-operations-to-reduce-an-integer-to-0", "count-the-number-of-square-free-subsets", "find-the-string-with-lcp"]}, {"contest_title": "\u7b2c 334 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 334", "contest_title_slug": "weekly-contest-334", "contest_id": 823, "contest_start_time": 1677378600, "contest_duration": 5400, "user_num": 5501, "question_slugs": ["left-and-right-sum-differences", "find-the-divisibility-array-of-a-string", "find-the-maximum-number-of-marked-indices", "minimum-time-to-visit-a-cell-in-a-grid"]}, {"contest_title": "\u7b2c 335 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 335", "contest_title_slug": "weekly-contest-335", "contest_id": 825, "contest_start_time": 1677983400, "contest_duration": 5400, "user_num": 6019, "question_slugs": ["pass-the-pillow", "kth-largest-sum-in-a-binary-tree", "split-the-array-to-make-coprime-products", "number-of-ways-to-earn-points"]}, {"contest_title": "\u7b2c 336 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 336", "contest_title_slug": "weekly-contest-336", "contest_id": 833, "contest_start_time": 1678588200, "contest_duration": 5400, "user_num": 5897, "question_slugs": ["count-the-number-of-vowel-strings-in-range", "rearrange-array-to-maximize-prefix-score", "count-the-number-of-beautiful-subarrays", "minimum-time-to-complete-all-tasks"]}, {"contest_title": "\u7b2c 337 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 337", "contest_title_slug": "weekly-contest-337", "contest_id": 839, "contest_start_time": 1679193000, "contest_duration": 5400, "user_num": 5628, "question_slugs": ["number-of-even-and-odd-bits", "check-knight-tour-configuration", "the-number-of-beautiful-subsets", "smallest-missing-non-negative-integer-after-operations"]}, {"contest_title": "\u7b2c 338 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 338", "contest_title_slug": "weekly-contest-338", "contest_id": 843, "contest_start_time": 1679797800, "contest_duration": 5400, "user_num": 5594, "question_slugs": ["k-items-with-the-maximum-sum", "prime-subtraction-operation", "minimum-operations-to-make-all-array-elements-equal", "collect-coins-in-a-tree"]}, {"contest_title": "\u7b2c 339 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 339", "contest_title_slug": "weekly-contest-339", "contest_id": 850, "contest_start_time": 1680402600, "contest_duration": 5400, "user_num": 5180, "question_slugs": ["find-the-longest-balanced-substring-of-a-binary-string", "convert-an-array-into-a-2d-array-with-conditions", "mice-and-cheese", "minimum-reverse-operations"]}, {"contest_title": "\u7b2c 340 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 340", "contest_title_slug": "weekly-contest-340", "contest_id": 854, "contest_start_time": 1681007400, "contest_duration": 5400, "user_num": 4937, "question_slugs": ["prime-in-diagonal", "sum-of-distances", "minimize-the-maximum-difference-of-pairs", "minimum-number-of-visited-cells-in-a-grid"]}, {"contest_title": "\u7b2c 341 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 341", "contest_title_slug": "weekly-contest-341", "contest_id": 856, "contest_start_time": 1681612200, "contest_duration": 5400, "user_num": 4792, "question_slugs": ["row-with-maximum-ones", "find-the-maximum-divisibility-score", "minimum-additions-to-make-valid-string", "minimize-the-total-price-of-the-trips"]}, {"contest_title": "\u7b2c 342 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 342", "contest_title_slug": "weekly-contest-342", "contest_id": 860, "contest_start_time": 1682217000, "contest_duration": 5400, "user_num": 3702, "question_slugs": ["calculate-delayed-arrival-time", "sum-multiples", "sliding-subarray-beauty", "minimum-number-of-operations-to-make-all-array-elements-equal-to-1"]}, {"contest_title": "\u7b2c 343 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 343", "contest_title_slug": "weekly-contest-343", "contest_id": 863, "contest_start_time": 1682821800, "contest_duration": 5400, "user_num": 3313, "question_slugs": ["determine-the-winner-of-a-bowling-game", "first-completely-painted-row-or-column", "minimum-cost-of-a-path-with-special-roads", "lexicographically-smallest-beautiful-string"]}, {"contest_title": "\u7b2c 344 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 344", "contest_title_slug": "weekly-contest-344", "contest_id": 867, "contest_start_time": 1683426600, "contest_duration": 5400, "user_num": 3986, "question_slugs": ["find-the-distinct-difference-array", "frequency-tracker", "number-of-adjacent-elements-with-the-same-color", "make-costs-of-paths-equal-in-a-binary-tree"]}, {"contest_title": "\u7b2c 345 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 345", "contest_title_slug": "weekly-contest-345", "contest_id": 870, "contest_start_time": 1684031400, "contest_duration": 5400, "user_num": 4165, "question_slugs": ["find-the-losers-of-the-circular-game", "neighboring-bitwise-xor", "maximum-number-of-moves-in-a-grid", "count-the-number-of-complete-components"]}, {"contest_title": "\u7b2c 346 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 346", "contest_title_slug": "weekly-contest-346", "contest_id": 874, "contest_start_time": 1684636200, "contest_duration": 5400, "user_num": 4035, "question_slugs": ["minimum-string-length-after-removing-substrings", "lexicographically-smallest-palindrome", "find-the-punishment-number-of-an-integer", "modify-graph-edge-weights"]}, {"contest_title": "\u7b2c 347 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 347", "contest_title_slug": "weekly-contest-347", "contest_id": 876, "contest_start_time": 1685241000, "contest_duration": 5400, "user_num": 3836, "question_slugs": ["remove-trailing-zeros-from-a-string", "difference-of-number-of-distinct-values-on-diagonals", "minimum-cost-to-make-all-characters-equal", "maximum-strictly-increasing-cells-in-a-matrix"]}, {"contest_title": "\u7b2c 348 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 348", "contest_title_slug": "weekly-contest-348", "contest_id": 880, "contest_start_time": 1685845800, "contest_duration": 5400, "user_num": 3909, "question_slugs": ["minimize-string-length", "semi-ordered-permutation", "sum-of-matrix-after-queries", "count-of-integers"]}, {"contest_title": "\u7b2c 349 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 349", "contest_title_slug": "weekly-contest-349", "contest_id": 882, "contest_start_time": 1686450600, "contest_duration": 5400, "user_num": 3714, "question_slugs": ["neither-minimum-nor-maximum", "lexicographically-smallest-string-after-substring-operation", "collecting-chocolates", "maximum-sum-queries"]}, {"contest_title": "\u7b2c 350 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 350", "contest_title_slug": "weekly-contest-350", "contest_id": 886, "contest_start_time": 1687055400, "contest_duration": 5400, "user_num": 3580, "question_slugs": ["total-distance-traveled", "find-the-value-of-the-partition", "special-permutations", "painting-the-walls"]}, {"contest_title": "\u7b2c 351 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 351", "contest_title_slug": "weekly-contest-351", "contest_id": 888, "contest_start_time": 1687660200, "contest_duration": 5400, "user_num": 2471, "question_slugs": ["number-of-beautiful-pairs", "minimum-operations-to-make-the-integer-zero", "ways-to-split-array-into-good-subarrays", "robot-collisions"]}, {"contest_title": "\u7b2c 352 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 352", "contest_title_slug": "weekly-contest-352", "contest_id": 892, "contest_start_time": 1688265000, "contest_duration": 5400, "user_num": 3437, "question_slugs": ["longest-even-odd-subarray-with-threshold", "prime-pairs-with-target-sum", "continuous-subarrays", "sum-of-imbalance-numbers-of-all-subarrays"]}, {"contest_title": "\u7b2c 353 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 353", "contest_title_slug": "weekly-contest-353", "contest_id": 894, "contest_start_time": 1688869800, "contest_duration": 5400, "user_num": 4113, "question_slugs": ["find-the-maximum-achievable-number", "maximum-number-of-jumps-to-reach-the-last-index", "longest-non-decreasing-subarray-from-two-arrays", "apply-operations-to-make-all-array-elements-equal-to-zero"]}, {"contest_title": "\u7b2c 354 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 354", "contest_title_slug": "weekly-contest-354", "contest_id": 898, "contest_start_time": 1689474600, "contest_duration": 5400, "user_num": 3957, "question_slugs": ["sum-of-squares-of-special-elements", "maximum-beauty-of-an-array-after-applying-operation", "minimum-index-of-a-valid-split", "length-of-the-longest-valid-substring"]}, {"contest_title": "\u7b2c 355 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 355", "contest_title_slug": "weekly-contest-355", "contest_id": 900, "contest_start_time": 1690079400, "contest_duration": 5400, "user_num": 4112, "question_slugs": ["split-strings-by-separator", "largest-element-in-an-array-after-merge-operations", "maximum-number-of-groups-with-increasing-length", "count-paths-that-can-form-a-palindrome-in-a-tree"]}, {"contest_title": "\u7b2c 356 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 356", "contest_title_slug": "weekly-contest-356", "contest_id": 904, "contest_start_time": 1690684200, "contest_duration": 5400, "user_num": 4082, "question_slugs": ["number-of-employees-who-met-the-target", "count-complete-subarrays-in-an-array", "shortest-string-that-contains-three-strings", "count-stepping-numbers-in-range"]}, {"contest_title": "\u7b2c 357 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 357", "contest_title_slug": "weekly-contest-357", "contest_id": 906, "contest_start_time": 1691289000, "contest_duration": 5400, "user_num": 4265, "question_slugs": ["faulty-keyboard", "check-if-it-is-possible-to-split-array", "find-the-safest-path-in-a-grid", "maximum-elegance-of-a-k-length-subsequence"]}, {"contest_title": "\u7b2c 358 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 358", "contest_title_slug": "weekly-contest-358", "contest_id": 910, "contest_start_time": 1691893800, "contest_duration": 5400, "user_num": 4475, "question_slugs": ["max-pair-sum-in-an-array", "double-a-number-represented-as-a-linked-list", "minimum-absolute-difference-between-elements-with-constraint", "apply-operations-to-maximize-score"]}, {"contest_title": "\u7b2c 359 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 359", "contest_title_slug": "weekly-contest-359", "contest_id": 913, "contest_start_time": 1692498600, "contest_duration": 5400, "user_num": 4101, "question_slugs": ["check-if-a-string-is-an-acronym-of-words", "determine-the-minimum-sum-of-a-k-avoiding-array", "maximize-the-profit-as-the-salesman", "find-the-longest-equal-subarray"]}, {"contest_title": "\u7b2c 360 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 360", "contest_title_slug": "weekly-contest-360", "contest_id": 918, "contest_start_time": 1693103400, "contest_duration": 5400, "user_num": 4496, "question_slugs": ["furthest-point-from-origin", "find-the-minimum-possible-sum-of-a-beautiful-array", "minimum-operations-to-form-subsequence-with-target-sum", "maximize-value-of-function-in-a-ball-passing-game"]}, {"contest_title": "\u7b2c 361 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 361", "contest_title_slug": "weekly-contest-361", "contest_id": 920, "contest_start_time": 1693708200, "contest_duration": 5400, "user_num": 4170, "question_slugs": ["count-symmetric-integers", "minimum-operations-to-make-a-special-number", "count-of-interesting-subarrays", "minimum-edge-weight-equilibrium-queries-in-a-tree"]}, {"contest_title": "\u7b2c 362 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 362", "contest_title_slug": "weekly-contest-362", "contest_id": 924, "contest_start_time": 1694313000, "contest_duration": 5400, "user_num": 4800, "question_slugs": ["points-that-intersect-with-cars", "determine-if-a-cell-is-reachable-at-a-given-time", "minimum-moves-to-spread-stones-over-grid", "string-transformation"]}, {"contest_title": "\u7b2c 363 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 363", "contest_title_slug": "weekly-contest-363", "contest_id": 926, "contest_start_time": 1694917800, "contest_duration": 5400, "user_num": 4768, "question_slugs": ["sum-of-values-at-indices-with-k-set-bits", "happy-students", "maximum-number-of-alloys", "maximum-element-sum-of-a-complete-subset-of-indices"]}, {"contest_title": "\u7b2c 364 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 364", "contest_title_slug": "weekly-contest-364", "contest_id": 930, "contest_start_time": 1695522600, "contest_duration": 5400, "user_num": 4304, "question_slugs": ["maximum-odd-binary-number", "beautiful-towers-i", "beautiful-towers-ii", "count-valid-paths-in-a-tree"]}, {"contest_title": "\u7b2c 365 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 365", "contest_title_slug": "weekly-contest-365", "contest_id": 932, "contest_start_time": 1696127400, "contest_duration": 5400, "user_num": 2909, "question_slugs": ["maximum-value-of-an-ordered-triplet-i", "maximum-value-of-an-ordered-triplet-ii", "minimum-size-subarray-in-infinite-array", "count-visited-nodes-in-a-directed-graph"]}, {"contest_title": "\u7b2c 366 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 366", "contest_title_slug": "weekly-contest-366", "contest_id": 936, "contest_start_time": 1696732200, "contest_duration": 5400, "user_num": 2790, "question_slugs": ["divisible-and-non-divisible-sums-difference", "minimum-processing-time", "apply-operations-to-make-two-strings-equal", "apply-operations-on-array-to-maximize-sum-of-squares"]}, {"contest_title": "\u7b2c 367 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 367", "contest_title_slug": "weekly-contest-367", "contest_id": 938, "contest_start_time": 1697337000, "contest_duration": 5400, "user_num": 4317, "question_slugs": ["find-indices-with-index-and-value-difference-i", "shortest-and-lexicographically-smallest-beautiful-string", "find-indices-with-index-and-value-difference-ii", "construct-product-matrix"]}, {"contest_title": "\u7b2c 368 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 368", "contest_title_slug": "weekly-contest-368", "contest_id": 942, "contest_start_time": 1697941800, "contest_duration": 5400, "user_num": 5002, "question_slugs": ["minimum-sum-of-mountain-triplets-i", "minimum-sum-of-mountain-triplets-ii", "minimum-number-of-groups-to-create-a-valid-assignment", "minimum-changes-to-make-k-semi-palindromes"]}, {"contest_title": "\u7b2c 369 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 369", "contest_title_slug": "weekly-contest-369", "contest_id": 945, "contest_start_time": 1698546600, "contest_duration": 5400, "user_num": 4121, "question_slugs": ["find-the-k-or-of-an-array", "minimum-equal-sum-of-two-arrays-after-replacing-zeros", "minimum-increment-operations-to-make-array-beautiful", "maximum-points-after-collecting-coins-from-all-nodes"]}, {"contest_title": "\u7b2c 370 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 370", "contest_title_slug": "weekly-contest-370", "contest_id": 950, "contest_start_time": 1699151400, "contest_duration": 5400, "user_num": 3983, "question_slugs": ["find-champion-i", "find-champion-ii", "maximum-score-after-applying-operations-on-a-tree", "maximum-balanced-subsequence-sum"]}, {"contest_title": "\u7b2c 371 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 371", "contest_title_slug": "weekly-contest-371", "contest_id": 952, "contest_start_time": 1699756200, "contest_duration": 5400, "user_num": 3638, "question_slugs": ["maximum-strong-pair-xor-i", "high-access-employees", "minimum-operations-to-maximize-last-elements-in-arrays", "maximum-strong-pair-xor-ii"]}, {"contest_title": "\u7b2c 372 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 372", "contest_title_slug": "weekly-contest-372", "contest_id": 956, "contest_start_time": 1700361000, "contest_duration": 5400, "user_num": 3920, "question_slugs": ["make-three-strings-equal", "separate-black-and-white-balls", "maximum-xor-product", "find-building-where-alice-and-bob-can-meet"]}, {"contest_title": "\u7b2c 373 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 373", "contest_title_slug": "weekly-contest-373", "contest_id": 958, "contest_start_time": 1700965800, "contest_duration": 5400, "user_num": 3577, "question_slugs": ["matrix-similarity-after-cyclic-shifts", "count-beautiful-substrings-i", "make-lexicographically-smallest-array-by-swapping-elements", "count-beautiful-substrings-ii"]}, {"contest_title": "\u7b2c 374 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 374", "contest_title_slug": "weekly-contest-374", "contest_id": 962, "contest_start_time": 1701570600, "contest_duration": 5400, "user_num": 4053, "question_slugs": ["find-the-peaks", "minimum-number-of-coins-to-be-added", "count-complete-substrings", "count-the-number-of-infection-sequences"]}, {"contest_title": "\u7b2c 375 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 375", "contest_title_slug": "weekly-contest-375", "contest_id": 964, "contest_start_time": 1702175400, "contest_duration": 5400, "user_num": 3518, "question_slugs": ["count-tested-devices-after-test-operations", "double-modular-exponentiation", "count-subarrays-where-max-element-appears-at-least-k-times", "count-the-number-of-good-partitions"]}, {"contest_title": "\u7b2c 376 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 376", "contest_title_slug": "weekly-contest-376", "contest_id": 968, "contest_start_time": 1702780200, "contest_duration": 5400, "user_num": 3409, "question_slugs": ["find-missing-and-repeated-values", "divide-array-into-arrays-with-max-difference", "minimum-cost-to-make-array-equalindromic", "apply-operations-to-maximize-frequency-score"]}, {"contest_title": "\u7b2c 377 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 377", "contest_title_slug": "weekly-contest-377", "contest_id": 970, "contest_start_time": 1703385000, "contest_duration": 5400, "user_num": 3148, "question_slugs": ["minimum-number-game", "maximum-square-area-by-removing-fences-from-a-field", "minimum-cost-to-convert-string-i", "minimum-cost-to-convert-string-ii"]}, {"contest_title": "\u7b2c 378 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 378", "contest_title_slug": "weekly-contest-378", "contest_id": 974, "contest_start_time": 1703989800, "contest_duration": 5400, "user_num": 2747, "question_slugs": ["check-if-bitwise-or-has-trailing-zeros", "find-longest-special-substring-that-occurs-thrice-i", "find-longest-special-substring-that-occurs-thrice-ii", "palindrome-rearrangement-queries"]}, {"contest_title": "\u7b2c 379 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 379", "contest_title_slug": "weekly-contest-379", "contest_id": 976, "contest_start_time": 1704594600, "contest_duration": 5400, "user_num": 3117, "question_slugs": ["maximum-area-of-longest-diagonal-rectangle", "minimum-moves-to-capture-the-queen", "maximum-size-of-a-set-after-removals", "maximize-the-number-of-partitions-after-operations"]}, {"contest_title": "\u7b2c 380 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 380", "contest_title_slug": "weekly-contest-380", "contest_id": 980, "contest_start_time": 1705199400, "contest_duration": 5400, "user_num": 3325, "question_slugs": ["count-elements-with-maximum-frequency", "find-beautiful-indices-in-the-given-array-i", "maximum-number-that-sum-of-the-prices-is-less-than-or-equal-to-k", "find-beautiful-indices-in-the-given-array-ii"]}, {"contest_title": "\u7b2c 381 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 381", "contest_title_slug": "weekly-contest-381", "contest_id": 982, "contest_start_time": 1705804200, "contest_duration": 5400, "user_num": 3737, "question_slugs": ["minimum-number-of-pushes-to-type-word-i", "count-the-number-of-houses-at-a-certain-distance-i", "minimum-number-of-pushes-to-type-word-ii", "count-the-number-of-houses-at-a-certain-distance-ii"]}, {"contest_title": "\u7b2c 382 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 382", "contest_title_slug": "weekly-contest-382", "contest_id": 986, "contest_start_time": 1706409000, "contest_duration": 5400, "user_num": 3134, "question_slugs": ["number-of-changing-keys", "find-the-maximum-number-of-elements-in-subset", "alice-and-bob-playing-flower-game", "minimize-or-of-remaining-elements-using-operations"]}, {"contest_title": "\u7b2c 383 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 383", "contest_title_slug": "weekly-contest-383", "contest_id": 988, "contest_start_time": 1707013800, "contest_duration": 5400, "user_num": 2691, "question_slugs": ["ant-on-the-boundary", "minimum-time-to-revert-word-to-initial-state-i", "find-the-grid-of-region-average", "minimum-time-to-revert-word-to-initial-state-ii"]}, {"contest_title": "\u7b2c 384 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 384", "contest_title_slug": "weekly-contest-384", "contest_id": 992, "contest_start_time": 1707618600, "contest_duration": 5400, "user_num": 1652, "question_slugs": ["modify-the-matrix", "number-of-subarrays-that-match-a-pattern-i", "maximum-palindromes-after-operations", "number-of-subarrays-that-match-a-pattern-ii"]}, {"contest_title": "\u7b2c 385 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 385", "contest_title_slug": "weekly-contest-385", "contest_id": 994, "contest_start_time": 1708223400, "contest_duration": 5400, "user_num": 2382, "question_slugs": ["count-prefix-and-suffix-pairs-i", "find-the-length-of-the-longest-common-prefix", "most-frequent-prime", "count-prefix-and-suffix-pairs-ii"]}, {"contest_title": "\u7b2c 386 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 386", "contest_title_slug": "weekly-contest-386", "contest_id": 998, "contest_start_time": 1708828200, "contest_duration": 5400, "user_num": 2731, "question_slugs": ["split-the-array", "find-the-largest-area-of-square-inside-two-rectangles", "earliest-second-to-mark-indices-i", "earliest-second-to-mark-indices-ii"]}, {"contest_title": "\u7b2c 387 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 387", "contest_title_slug": "weekly-contest-387", "contest_id": 1000, "contest_start_time": 1709433000, "contest_duration": 5400, "user_num": 3694, "question_slugs": ["distribute-elements-into-two-arrays-i", "count-submatrices-with-top-left-element-and-sum-less-than-k", "minimum-operations-to-write-the-letter-y-on-a-grid", "distribute-elements-into-two-arrays-ii"]}, {"contest_title": "\u7b2c 388 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 388", "contest_title_slug": "weekly-contest-388", "contest_id": 1004, "contest_start_time": 1710037800, "contest_duration": 5400, "user_num": 4291, "question_slugs": ["apple-redistribution-into-boxes", "maximize-happiness-of-selected-children", "shortest-uncommon-substring-in-an-array", "maximum-strength-of-k-disjoint-subarrays"]}, {"contest_title": "\u7b2c 389 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 389", "contest_title_slug": "weekly-contest-389", "contest_id": 1006, "contest_start_time": 1710642600, "contest_duration": 5400, "user_num": 4561, "question_slugs": ["existence-of-a-substring-in-a-string-and-its-reverse", "count-substrings-starting-and-ending-with-given-character", "minimum-deletions-to-make-string-k-special", "minimum-moves-to-pick-k-ones"]}, {"contest_title": "\u7b2c 390 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 390", "contest_title_slug": "weekly-contest-390", "contest_id": 1011, "contest_start_time": 1711247400, "contest_duration": 5400, "user_num": 4817, "question_slugs": ["maximum-length-substring-with-two-occurrences", "apply-operations-to-make-sum-of-array-greater-than-or-equal-to-k", "most-frequent-ids", "longest-common-suffix-queries"]}, {"contest_title": "\u7b2c 391 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 391", "contest_title_slug": "weekly-contest-391", "contest_id": 1014, "contest_start_time": 1711852200, "contest_duration": 5400, "user_num": 4181, "question_slugs": ["harshad-number", "water-bottles-ii", "count-alternating-subarrays", "minimize-manhattan-distances"]}, {"contest_title": "\u7b2c 392 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 392", "contest_title_slug": "weekly-contest-392", "contest_id": 1018, "contest_start_time": 1712457000, "contest_duration": 5400, "user_num": 3194, "question_slugs": ["longest-strictly-increasing-or-strictly-decreasing-subarray", "lexicographically-smallest-string-after-operations-with-constraint", "minimum-operations-to-make-median-of-array-equal-to-k", "minimum-cost-walk-in-weighted-graph"]}, {"contest_title": "\u7b2c 393 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 393", "contest_title_slug": "weekly-contest-393", "contest_id": 1020, "contest_start_time": 1713061800, "contest_duration": 5400, "user_num": 4219, "question_slugs": ["latest-time-you-can-obtain-after-replacing-characters", "maximum-prime-difference", "kth-smallest-amount-with-single-denomination-combination", "minimum-sum-of-values-by-dividing-array"]}, {"contest_title": "\u7b2c 394 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 394", "contest_title_slug": "weekly-contest-394", "contest_id": 1024, "contest_start_time": 1713666600, "contest_duration": 5400, "user_num": 3958, "question_slugs": ["count-the-number-of-special-characters-i", "count-the-number-of-special-characters-ii", "minimum-number-of-operations-to-satisfy-conditions", "find-edges-in-shortest-paths"]}, {"contest_title": "\u7b2c 395 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 395", "contest_title_slug": "weekly-contest-395", "contest_id": 1026, "contest_start_time": 1714271400, "contest_duration": 5400, "user_num": 2969, "question_slugs": ["find-the-integer-added-to-array-i", "find-the-integer-added-to-array-ii", "minimum-array-end", "find-the-median-of-the-uniqueness-array"]}, {"contest_title": "\u7b2c 396 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 396", "contest_title_slug": "weekly-contest-396", "contest_id": 1030, "contest_start_time": 1714876200, "contest_duration": 5400, "user_num": 2932, "question_slugs": ["valid-word", "minimum-number-of-operations-to-make-word-k-periodic", "minimum-length-of-anagram-concatenation", "minimum-cost-to-equalize-array"]}, {"contest_title": "\u7b2c 397 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 397", "contest_title_slug": "weekly-contest-397", "contest_id": 1032, "contest_start_time": 1715481000, "contest_duration": 5400, "user_num": 3365, "question_slugs": ["permutation-difference-between-two-strings", "taking-maximum-energy-from-the-mystic-dungeon", "maximum-difference-score-in-a-grid", "find-the-minimum-cost-array-permutation"]}, {"contest_title": "\u7b2c 398 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 398", "contest_title_slug": "weekly-contest-398", "contest_id": 1036, "contest_start_time": 1716085800, "contest_duration": 5400, "user_num": 3606, "question_slugs": ["special-array-i", "special-array-ii", "sum-of-digit-differences-of-all-pairs", "find-number-of-ways-to-reach-the-k-th-stair"]}, {"contest_title": "\u7b2c 399 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 399", "contest_title_slug": "weekly-contest-399", "contest_id": 1038, "contest_start_time": 1716690600, "contest_duration": 5400, "user_num": 3424, "question_slugs": ["find-the-number-of-good-pairs-i", "string-compression-iii", "find-the-number-of-good-pairs-ii", "maximum-sum-of-subsequence-with-non-adjacent-elements"]}, {"contest_title": "\u7b2c 400 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 400", "contest_title_slug": "weekly-contest-400", "contest_id": 1043, "contest_start_time": 1717295400, "contest_duration": 5400, "user_num": 3534, "question_slugs": ["minimum-number-of-chairs-in-a-waiting-room", "count-days-without-meetings", "lexicographically-minimum-string-after-removing-stars", "find-subarray-with-bitwise-or-closest-to-k"]}, {"contest_title": "\u7b2c 401 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 401", "contest_title_slug": "weekly-contest-401", "contest_id": 1045, "contest_start_time": 1717900200, "contest_duration": 5400, "user_num": 3160, "question_slugs": ["find-the-child-who-has-the-ball-after-k-seconds", "find-the-n-th-value-after-k-seconds", "maximum-total-reward-using-operations-i", "maximum-total-reward-using-operations-ii"]}, {"contest_title": "\u7b2c 402 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 402", "contest_title_slug": "weekly-contest-402", "contest_id": 1049, "contest_start_time": 1718505000, "contest_duration": 5400, "user_num": 3283, "question_slugs": ["count-pairs-that-form-a-complete-day-i", "count-pairs-that-form-a-complete-day-ii", "maximum-total-damage-with-spell-casting", "peaks-in-array"]}, {"contest_title": "\u7b2c 403 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 403", "contest_title_slug": "weekly-contest-403", "contest_id": 1052, "contest_start_time": 1719109800, "contest_duration": 5400, "user_num": 3112, "question_slugs": ["minimum-average-of-smallest-and-largest-elements", "find-the-minimum-area-to-cover-all-ones-i", "maximize-total-cost-of-alternating-subarrays", "find-the-minimum-area-to-cover-all-ones-ii"]}, {"contest_title": "\u7b2c 404 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 404", "contest_title_slug": "weekly-contest-404", "contest_id": 1056, "contest_start_time": 1719714600, "contest_duration": 5400, "user_num": 3486, "question_slugs": ["maximum-height-of-a-triangle", "find-the-maximum-length-of-valid-subsequence-i", "find-the-maximum-length-of-valid-subsequence-ii", "find-minimum-diameter-after-merging-two-trees"]}, {"contest_title": "\u7b2c 405 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 405", "contest_title_slug": "weekly-contest-405", "contest_id": 1058, "contest_start_time": 1720319400, "contest_duration": 5400, "user_num": 3240, "question_slugs": ["find-the-encrypted-string", "generate-binary-strings-without-adjacent-zeros", "count-submatrices-with-equal-frequency-of-x-and-y", "construct-string-with-minimum-cost"]}, {"contest_title": "\u7b2c 406 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 406", "contest_title_slug": "weekly-contest-406", "contest_id": 1062, "contest_start_time": 1720924200, "contest_duration": 5400, "user_num": 3422, "question_slugs": ["lexicographically-smallest-string-after-a-swap", "delete-nodes-from-linked-list-present-in-array", "minimum-cost-for-cutting-cake-i", "minimum-cost-for-cutting-cake-ii"]}, {"contest_title": "\u7b2c 407 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 407", "contest_title_slug": "weekly-contest-407", "contest_id": 1064, "contest_start_time": 1721529000, "contest_duration": 5400, "user_num": 3268, "question_slugs": ["number-of-bit-changes-to-make-two-integers-equal", "vowels-game-in-a-string", "maximum-number-of-operations-to-move-ones-to-the-end", "minimum-operations-to-make-array-equal-to-target"]}, {"contest_title": "\u7b2c 408 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 408", "contest_title_slug": "weekly-contest-408", "contest_id": 1069, "contest_start_time": 1722133800, "contest_duration": 5400, "user_num": 3369, "question_slugs": ["find-if-digit-game-can-be-won", "find-the-count-of-numbers-which-are-not-special", "count-the-number-of-substrings-with-dominant-ones", "check-if-the-rectangle-corner-is-reachable"]}, {"contest_title": "\u7b2c 409 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 409", "contest_title_slug": "weekly-contest-409", "contest_id": 1071, "contest_start_time": 1722738600, "contest_duration": 5400, "user_num": 3643, "question_slugs": ["design-neighbor-sum-service", "shortest-distance-after-road-addition-queries-i", "shortest-distance-after-road-addition-queries-ii", "alternating-groups-iii"]}, {"contest_title": "\u7b2c 1 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 1", "contest_title_slug": "biweekly-contest-1", "contest_id": 70, "contest_start_time": 1559399400, "contest_duration": 7200, "user_num": 197, "question_slugs": ["fixed-point", "index-pairs-of-a-string", "campus-bikes-ii", "digit-count-in-range"]}, {"contest_title": "\u7b2c 2 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 2", "contest_title_slug": "biweekly-contest-2", "contest_id": 73, "contest_start_time": 1560609000, "contest_duration": 5400, "user_num": 256, "question_slugs": ["sum-of-digits-in-the-minimum-number", "high-five", "brace-expansion", "confusing-number-ii"]}, {"contest_title": "\u7b2c 3 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 3", "contest_title_slug": "biweekly-contest-3", "contest_id": 85, "contest_start_time": 1561818600, "contest_duration": 5400, "user_num": 312, "question_slugs": ["two-sum-less-than-k", "find-k-length-substrings-with-no-repeated-characters", "the-earliest-moment-when-everyone-become-friends", "path-with-maximum-minimum-value"]}, {"contest_title": "\u7b2c 4 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 4", "contest_title_slug": "biweekly-contest-4", "contest_id": 88, "contest_start_time": 1563028200, "contest_duration": 5400, "user_num": 438, "question_slugs": ["number-of-days-in-a-month", "remove-vowels-from-a-string", "maximum-average-subtree", "divide-array-into-increasing-sequences"]}, {"contest_title": "\u7b2c 5 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 5", "contest_title_slug": "biweekly-contest-5", "contest_id": 91, "contest_start_time": 1564237800, "contest_duration": 5400, "user_num": 495, "question_slugs": ["largest-unique-number", "armstrong-number", "connecting-cities-with-minimum-cost", "parallel-courses"]}, {"contest_title": "\u7b2c 6 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 6", "contest_title_slug": "biweekly-contest-6", "contest_id": 95, "contest_start_time": 1565447400, "contest_duration": 5400, "user_num": 513, "question_slugs": ["check-if-a-number-is-majority-element-in-a-sorted-array", "minimum-swaps-to-group-all-1s-together", "analyze-user-website-visit-pattern", "string-transforms-into-another-string"]}, {"contest_title": "\u7b2c 7 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 7", "contest_title_slug": "biweekly-contest-7", "contest_id": 99, "contest_start_time": 1566657000, "contest_duration": 5400, "user_num": 561, "question_slugs": ["single-row-keyboard", "design-file-system", "minimum-cost-to-connect-sticks", "optimize-water-distribution-in-a-village"]}, {"contest_title": "\u7b2c 8 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 8", "contest_title_slug": "biweekly-contest-8", "contest_id": 103, "contest_start_time": 1567866600, "contest_duration": 5400, "user_num": 630, "question_slugs": ["count-substrings-with-only-one-distinct-letter", "before-and-after-puzzle", "shortest-distance-to-target-color", "maximum-number-of-ones"]}, {"contest_title": "\u7b2c 9 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 9", "contest_title_slug": "biweekly-contest-9", "contest_id": 108, "contest_start_time": 1569076200, "contest_duration": 5700, "user_num": 929, "question_slugs": ["how-many-apples-can-you-put-into-the-basket", "minimum-knight-moves", "find-smallest-common-element-in-all-rows", "minimum-time-to-build-blocks"]}, {"contest_title": "\u7b2c 10 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 10", "contest_title_slug": "biweekly-contest-10", "contest_id": 115, "contest_start_time": 1570285800, "contest_duration": 5400, "user_num": 738, "question_slugs": ["intersection-of-three-sorted-arrays", "two-sum-bsts", "stepping-numbers", "valid-palindrome-iii"]}, {"contest_title": "\u7b2c 11 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 11", "contest_title_slug": "biweekly-contest-11", "contest_id": 118, "contest_start_time": 1571495400, "contest_duration": 5400, "user_num": 913, "question_slugs": ["missing-number-in-arithmetic-progression", "meeting-scheduler", "toss-strange-coins", "divide-chocolate"]}, {"contest_title": "\u7b2c 12 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 12", "contest_title_slug": "biweekly-contest-12", "contest_id": 121, "contest_start_time": 1572705000, "contest_duration": 5400, "user_num": 911, "question_slugs": ["design-a-leaderboard", "array-transformation", "tree-diameter", "palindrome-removal"]}, {"contest_title": "\u7b2c 13 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 13", "contest_title_slug": "biweekly-contest-13", "contest_id": 124, "contest_start_time": 1573914600, "contest_duration": 5400, "user_num": 810, "question_slugs": ["encode-number", "smallest-common-region", "synonymous-sentences", "handshakes-that-dont-cross"]}, {"contest_title": "\u7b2c 14 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 14", "contest_title_slug": "biweekly-contest-14", "contest_id": 129, "contest_start_time": 1575124200, "contest_duration": 5400, "user_num": 871, "question_slugs": ["hexspeak", "remove-interval", "delete-tree-nodes", "number-of-ships-in-a-rectangle"]}, {"contest_title": "\u7b2c 15 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 15", "contest_title_slug": "biweekly-contest-15", "contest_id": 132, "contest_start_time": 1576333800, "contest_duration": 5400, "user_num": 797, "question_slugs": ["element-appearing-more-than-25-in-sorted-array", "remove-covered-intervals", "iterator-for-combination", "minimum-falling-path-sum-ii"]}, {"contest_title": "\u7b2c 16 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 16", "contest_title_slug": "biweekly-contest-16", "contest_id": 135, "contest_start_time": 1577543400, "contest_duration": 5400, "user_num": 822, "question_slugs": ["replace-elements-with-greatest-element-on-right-side", "sum-of-mutated-array-closest-to-target", "deepest-leaves-sum", "number-of-paths-with-max-score"]}, {"contest_title": "\u7b2c 17 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 17", "contest_title_slug": "biweekly-contest-17", "contest_id": 138, "contest_start_time": 1578753000, "contest_duration": 5400, "user_num": 897, "question_slugs": ["decompress-run-length-encoded-list", "matrix-block-sum", "sum-of-nodes-with-even-valued-grandparent", "distinct-echo-substrings"]}, {"contest_title": "\u7b2c 18 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 18", "contest_title_slug": "biweekly-contest-18", "contest_id": 143, "contest_start_time": 1579962600, "contest_duration": 5400, "user_num": 587, "question_slugs": ["rank-transform-of-an-array", "break-a-palindrome", "sort-the-matrix-diagonally", "reverse-subarray-to-maximize-array-value"]}, {"contest_title": "\u7b2c 19 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 19", "contest_title_slug": "biweekly-contest-19", "contest_id": 146, "contest_start_time": 1581172200, "contest_duration": 5400, "user_num": 1120, "question_slugs": ["number-of-steps-to-reduce-a-number-to-zero", "number-of-sub-arrays-of-size-k-and-average-greater-than-or-equal-to-threshold", "angle-between-hands-of-a-clock", "jump-game-iv"]}, {"contest_title": "\u7b2c 20 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 20", "contest_title_slug": "biweekly-contest-20", "contest_id": 149, "contest_start_time": 1582381800, "contest_duration": 5400, "user_num": 1541, "question_slugs": ["sort-integers-by-the-number-of-1-bits", "apply-discount-every-n-orders", "number-of-substrings-containing-all-three-characters", "count-all-valid-pickup-and-delivery-options"]}, {"contest_title": "\u7b2c 21 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 21", "contest_title_slug": "biweekly-contest-21", "contest_id": 157, "contest_start_time": 1583591400, "contest_duration": 5400, "user_num": 1913, "question_slugs": ["increasing-decreasing-string", "find-the-longest-substring-containing-vowels-in-even-counts", "longest-zigzag-path-in-a-binary-tree", "maximum-sum-bst-in-binary-tree"]}, {"contest_title": "\u7b2c 22 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 22", "contest_title_slug": "biweekly-contest-22", "contest_id": 163, "contest_start_time": 1584801000, "contest_duration": 5400, "user_num": 2042, "question_slugs": ["find-the-distance-value-between-two-arrays", "cinema-seat-allocation", "sort-integers-by-the-power-value", "pizza-with-3n-slices"]}, {"contest_title": "\u7b2c 23 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 23", "contest_title_slug": "biweekly-contest-23", "contest_id": 169, "contest_start_time": 1586010600, "contest_duration": 5400, "user_num": 2045, "question_slugs": ["count-largest-group", "construct-k-palindrome-strings", "circle-and-rectangle-overlapping", "reducing-dishes"]}, {"contest_title": "\u7b2c 24 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 24", "contest_title_slug": "biweekly-contest-24", "contest_id": 178, "contest_start_time": 1587220200, "contest_duration": 5400, "user_num": 1898, "question_slugs": ["minimum-value-to-get-positive-step-by-step-sum", "find-the-minimum-number-of-fibonacci-numbers-whose-sum-is-k", "the-k-th-lexicographical-string-of-all-happy-strings-of-length-n", "restore-the-array"]}, {"contest_title": "\u7b2c 25 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 25", "contest_title_slug": "biweekly-contest-25", "contest_id": 192, "contest_start_time": 1588429800, "contest_duration": 5400, "user_num": 1832, "question_slugs": ["kids-with-the-greatest-number-of-candies", "max-difference-you-can-get-from-changing-an-integer", "check-if-a-string-can-break-another-string", "number-of-ways-to-wear-different-hats-to-each-other"]}, {"contest_title": "\u7b2c 26 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 26", "contest_title_slug": "biweekly-contest-26", "contest_id": 198, "contest_start_time": 1589639400, "contest_duration": 5400, "user_num": 1971, "question_slugs": ["consecutive-characters", "simplified-fractions", "count-good-nodes-in-binary-tree", "form-largest-integer-with-digits-that-add-up-to-target"]}, {"contest_title": "\u7b2c 27 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 27", "contest_title_slug": "biweekly-contest-27", "contest_id": 204, "contest_start_time": 1590849000, "contest_duration": 5400, "user_num": 1966, "question_slugs": ["make-two-arrays-equal-by-reversing-subarrays", "check-if-a-string-contains-all-binary-codes-of-size-k", "course-schedule-iv", "cherry-pickup-ii"]}, {"contest_title": "\u7b2c 28 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 28", "contest_title_slug": "biweekly-contest-28", "contest_id": 210, "contest_start_time": 1592058600, "contest_duration": 5400, "user_num": 2144, "question_slugs": ["final-prices-with-a-special-discount-in-a-shop", "subrectangle-queries", "find-two-non-overlapping-sub-arrays-each-with-target-sum", "allocate-mailboxes"]}, {"contest_title": "\u7b2c 29 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 29", "contest_title_slug": "biweekly-contest-29", "contest_id": 216, "contest_start_time": 1593268200, "contest_duration": 5400, "user_num": 2260, "question_slugs": ["average-salary-excluding-the-minimum-and-maximum-salary", "the-kth-factor-of-n", "longest-subarray-of-1s-after-deleting-one-element", "parallel-courses-ii"]}, {"contest_title": "\u7b2c 30 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 30", "contest_title_slug": "biweekly-contest-30", "contest_id": 222, "contest_start_time": 1594477800, "contest_duration": 5400, "user_num": 2545, "question_slugs": ["reformat-date", "range-sum-of-sorted-subarray-sums", "minimum-difference-between-largest-and-smallest-value-in-three-moves", "stone-game-iv"]}, {"contest_title": "\u7b2c 31 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 31", "contest_title_slug": "biweekly-contest-31", "contest_id": 232, "contest_start_time": 1595687400, "contest_duration": 5400, "user_num": 2767, "question_slugs": ["count-odd-numbers-in-an-interval-range", "number-of-sub-arrays-with-odd-sum", "number-of-good-ways-to-split-a-string", "minimum-number-of-increments-on-subarrays-to-form-a-target-array"]}, {"contest_title": "\u7b2c 32 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 32", "contest_title_slug": "biweekly-contest-32", "contest_id": 237, "contest_start_time": 1596897000, "contest_duration": 5400, "user_num": 2957, "question_slugs": ["kth-missing-positive-number", "can-convert-string-in-k-moves", "minimum-insertions-to-balance-a-parentheses-string", "find-longest-awesome-substring"]}, {"contest_title": "\u7b2c 33 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 33", "contest_title_slug": "biweekly-contest-33", "contest_id": 241, "contest_start_time": 1598106600, "contest_duration": 5400, "user_num": 3304, "question_slugs": ["thousand-separator", "minimum-number-of-vertices-to-reach-all-nodes", "minimum-numbers-of-function-calls-to-make-target-array", "detect-cycles-in-2d-grid"]}, {"contest_title": "\u7b2c 34 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 34", "contest_title_slug": "biweekly-contest-34", "contest_id": 256, "contest_start_time": 1599316200, "contest_duration": 5400, "user_num": 2842, "question_slugs": ["matrix-diagonal-sum", "number-of-ways-to-split-a-string", "shortest-subarray-to-be-removed-to-make-array-sorted", "count-all-possible-routes"]}, {"contest_title": "\u7b2c 35 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 35", "contest_title_slug": "biweekly-contest-35", "contest_id": 266, "contest_start_time": 1600525800, "contest_duration": 5400, "user_num": 2839, "question_slugs": ["sum-of-all-odd-length-subarrays", "maximum-sum-obtained-of-any-permutation", "make-sum-divisible-by-p", "strange-printer-ii"]}, {"contest_title": "\u7b2c 36 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 36", "contest_title_slug": "biweekly-contest-36", "contest_id": 288, "contest_start_time": 1601735400, "contest_duration": 5400, "user_num": 2204, "question_slugs": ["design-parking-system", "alert-using-same-key-card-three-or-more-times-in-a-one-hour-period", "find-valid-matrix-given-row-and-column-sums", "find-servers-that-handled-most-number-of-requests"]}, {"contest_title": "\u7b2c 37 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 37", "contest_title_slug": "biweekly-contest-37", "contest_id": 294, "contest_start_time": 1602945000, "contest_duration": 5400, "user_num": 2104, "question_slugs": ["mean-of-array-after-removing-some-elements", "coordinate-with-maximum-network-quality", "number-of-sets-of-k-non-overlapping-line-segments", "fancy-sequence"]}, {"contest_title": "\u7b2c 38 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 38", "contest_title_slug": "biweekly-contest-38", "contest_id": 300, "contest_start_time": 1604154600, "contest_duration": 5400, "user_num": 2004, "question_slugs": ["sort-array-by-increasing-frequency", "widest-vertical-area-between-two-points-containing-no-points", "count-substrings-that-differ-by-one-character", "number-of-ways-to-form-a-target-string-given-a-dictionary"]}, {"contest_title": "\u7b2c 39 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 39", "contest_title_slug": "biweekly-contest-39", "contest_id": 306, "contest_start_time": 1605364200, "contest_duration": 5400, "user_num": 2069, "question_slugs": ["defuse-the-bomb", "minimum-deletions-to-make-string-balanced", "minimum-jumps-to-reach-home", "distribute-repeating-integers"]}, {"contest_title": "\u7b2c 40 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 40", "contest_title_slug": "biweekly-contest-40", "contest_id": 312, "contest_start_time": 1606573800, "contest_duration": 5400, "user_num": 1891, "question_slugs": ["maximum-repeating-substring", "merge-in-between-linked-lists", "design-front-middle-back-queue", "minimum-number-of-removals-to-make-mountain-array"]}, {"contest_title": "\u7b2c 41 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 41", "contest_title_slug": "biweekly-contest-41", "contest_id": 318, "contest_start_time": 1607783400, "contest_duration": 5400, "user_num": 1660, "question_slugs": ["count-the-number-of-consistent-strings", "sum-of-absolute-differences-in-a-sorted-array", "stone-game-vi", "delivering-boxes-from-storage-to-ports"]}, {"contest_title": "\u7b2c 42 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 42", "contest_title_slug": "biweekly-contest-42", "contest_id": 325, "contest_start_time": 1608993000, "contest_duration": 5400, "user_num": 1578, "question_slugs": ["number-of-students-unable-to-eat-lunch", "average-waiting-time", "maximum-binary-string-after-change", "minimum-adjacent-swaps-for-k-consecutive-ones"]}, {"contest_title": "\u7b2c 43 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 43", "contest_title_slug": "biweekly-contest-43", "contest_id": 331, "contest_start_time": 1610202600, "contest_duration": 5400, "user_num": 1631, "question_slugs": ["calculate-money-in-leetcode-bank", "maximum-score-from-removing-substrings", "construct-the-lexicographically-largest-valid-sequence", "number-of-ways-to-reconstruct-a-tree"]}, {"contest_title": "\u7b2c 44 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 44", "contest_title_slug": "biweekly-contest-44", "contest_id": 337, "contest_start_time": 1611412200, "contest_duration": 5400, "user_num": 1826, "question_slugs": ["find-the-highest-altitude", "minimum-number-of-people-to-teach", "decode-xored-permutation", "count-ways-to-make-array-with-product"]}, {"contest_title": "\u7b2c 45 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 45", "contest_title_slug": "biweekly-contest-45", "contest_id": 343, "contest_start_time": 1612621800, "contest_duration": 5400, "user_num": 1676, "question_slugs": ["sum-of-unique-elements", "maximum-absolute-sum-of-any-subarray", "minimum-length-of-string-after-deleting-similar-ends", "maximum-number-of-events-that-can-be-attended-ii"]}, {"contest_title": "\u7b2c 46 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 46", "contest_title_slug": "biweekly-contest-46", "contest_id": 349, "contest_start_time": 1613831400, "contest_duration": 5400, "user_num": 1647, "question_slugs": ["longest-nice-substring", "form-array-by-concatenating-subarrays-of-another-array", "map-of-highest-peak", "tree-of-coprimes"]}, {"contest_title": "\u7b2c 47 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 47", "contest_title_slug": "biweekly-contest-47", "contest_id": 355, "contest_start_time": 1615041000, "contest_duration": 5400, "user_num": 3085, "question_slugs": ["find-nearest-point-that-has-the-same-x-or-y-coordinate", "check-if-number-is-a-sum-of-powers-of-three", "sum-of-beauty-of-all-substrings", "count-pairs-of-nodes"]}, {"contest_title": "\u7b2c 48 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 48", "contest_title_slug": "biweekly-contest-48", "contest_id": 362, "contest_start_time": 1616250600, "contest_duration": 5400, "user_num": 2853, "question_slugs": ["second-largest-digit-in-a-string", "design-authentication-manager", "maximum-number-of-consecutive-values-you-can-make", "maximize-score-after-n-operations"]}, {"contest_title": "\u7b2c 49 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 49", "contest_title_slug": "biweekly-contest-49", "contest_id": 374, "contest_start_time": 1617460200, "contest_duration": 5400, "user_num": 3193, "question_slugs": ["determine-color-of-a-chessboard-square", "sentence-similarity-iii", "count-nice-pairs-in-an-array", "maximum-number-of-groups-getting-fresh-donuts"]}, {"contest_title": "\u7b2c 50 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 50", "contest_title_slug": "biweekly-contest-50", "contest_id": 390, "contest_start_time": 1618669800, "contest_duration": 5400, "user_num": 3608, "question_slugs": ["minimum-operations-to-make-the-array-increasing", "queries-on-number-of-points-inside-a-circle", "maximum-xor-for-each-query", "minimum-number-of-operations-to-make-string-sorted"]}, {"contest_title": "\u7b2c 51 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 51", "contest_title_slug": "biweekly-contest-51", "contest_id": 396, "contest_start_time": 1619879400, "contest_duration": 5400, "user_num": 2675, "question_slugs": ["replace-all-digits-with-characters", "seat-reservation-manager", "maximum-element-after-decreasing-and-rearranging", "closest-room"]}, {"contest_title": "\u7b2c 52 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 52", "contest_title_slug": "biweekly-contest-52", "contest_id": 402, "contest_start_time": 1621089000, "contest_duration": 5400, "user_num": 2930, "question_slugs": ["sorting-the-sentence", "incremental-memory-leak", "rotating-the-box", "sum-of-floored-pairs"]}, {"contest_title": "\u7b2c 53 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 53", "contest_title_slug": "biweekly-contest-53", "contest_id": 408, "contest_start_time": 1622298600, "contest_duration": 5400, "user_num": 3069, "question_slugs": ["substrings-of-size-three-with-distinct-characters", "minimize-maximum-pair-sum-in-array", "get-biggest-three-rhombus-sums-in-a-grid", "minimum-xor-sum-of-two-arrays"]}, {"contest_title": "\u7b2c 54 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 54", "contest_title_slug": "biweekly-contest-54", "contest_id": 414, "contest_start_time": 1623508200, "contest_duration": 5400, "user_num": 2479, "question_slugs": ["check-if-all-the-integers-in-a-range-are-covered", "find-the-student-that-will-replace-the-chalk", "largest-magic-square", "minimum-cost-to-change-the-final-value-of-expression"]}, {"contest_title": "\u7b2c 55 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 55", "contest_title_slug": "biweekly-contest-55", "contest_id": 421, "contest_start_time": 1624717800, "contest_duration": 5400, "user_num": 3277, "question_slugs": ["remove-one-element-to-make-the-array-strictly-increasing", "remove-all-occurrences-of-a-substring", "maximum-alternating-subsequence-sum", "design-movie-rental-system"]}, {"contest_title": "\u7b2c 56 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 56", "contest_title_slug": "biweekly-contest-56", "contest_id": 429, "contest_start_time": 1625927400, "contest_duration": 5400, "user_num": 2760, "question_slugs": ["count-square-sum-triples", "nearest-exit-from-entrance-in-maze", "sum-game", "minimum-cost-to-reach-destination-in-time"]}, {"contest_title": "\u7b2c 57 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 57", "contest_title_slug": "biweekly-contest-57", "contest_id": 435, "contest_start_time": 1627137000, "contest_duration": 5400, "user_num": 2933, "question_slugs": ["check-if-all-characters-have-equal-number-of-occurrences", "the-number-of-the-smallest-unoccupied-chair", "describe-the-painting", "number-of-visible-people-in-a-queue"]}, {"contest_title": "\u7b2c 58 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 58", "contest_title_slug": "biweekly-contest-58", "contest_id": 441, "contest_start_time": 1628346600, "contest_duration": 5400, "user_num": 2889, "question_slugs": ["delete-characters-to-make-fancy-string", "check-if-move-is-legal", "minimum-total-space-wasted-with-k-resizing-operations", "maximum-product-of-the-length-of-two-palindromic-substrings"]}, {"contest_title": "\u7b2c 59 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 59", "contest_title_slug": "biweekly-contest-59", "contest_id": 448, "contest_start_time": 1629556200, "contest_duration": 5400, "user_num": 3030, "question_slugs": ["minimum-time-to-type-word-using-special-typewriter", "maximum-matrix-sum", "number-of-ways-to-arrive-at-destination", "number-of-ways-to-separate-numbers"]}, {"contest_title": "\u7b2c 60 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 60", "contest_title_slug": "biweekly-contest-60", "contest_id": 461, "contest_start_time": 1630765800, "contest_duration": 5400, "user_num": 2848, "question_slugs": ["find-the-middle-index-in-array", "find-all-groups-of-farmland", "operations-on-tree", "the-number-of-good-subsets"]}, {"contest_title": "\u7b2c 61 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 61", "contest_title_slug": "biweekly-contest-61", "contest_id": 467, "contest_start_time": 1631975400, "contest_duration": 5400, "user_num": 2534, "question_slugs": ["count-number-of-pairs-with-absolute-difference-k", "find-original-array-from-doubled-array", "maximum-earnings-from-taxi", "minimum-number-of-operations-to-make-array-continuous"]}, {"contest_title": "\u7b2c 62 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 62", "contest_title_slug": "biweekly-contest-62", "contest_id": 477, "contest_start_time": 1633185000, "contest_duration": 5400, "user_num": 2619, "question_slugs": ["convert-1d-array-into-2d-array", "number-of-pairs-of-strings-with-concatenation-equal-to-target", "maximize-the-confusion-of-an-exam", "maximum-number-of-ways-to-partition-an-array"]}, {"contest_title": "\u7b2c 63 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 63", "contest_title_slug": "biweekly-contest-63", "contest_id": 484, "contest_start_time": 1634394600, "contest_duration": 5400, "user_num": 2828, "question_slugs": ["minimum-number-of-moves-to-seat-everyone", "remove-colored-pieces-if-both-neighbors-are-the-same-color", "the-time-when-the-network-becomes-idle", "kth-smallest-product-of-two-sorted-arrays"]}, {"contest_title": "\u7b2c 64 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 64", "contest_title_slug": "biweekly-contest-64", "contest_id": 490, "contest_start_time": 1635604200, "contest_duration": 5400, "user_num": 2838, "question_slugs": ["kth-distinct-string-in-an-array", "two-best-non-overlapping-events", "plates-between-candles", "number-of-valid-move-combinations-on-chessboard"]}, {"contest_title": "\u7b2c 65 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 65", "contest_title_slug": "biweekly-contest-65", "contest_id": 497, "contest_start_time": 1636813800, "contest_duration": 5400, "user_num": 2676, "question_slugs": ["check-whether-two-strings-are-almost-equivalent", "walking-robot-simulation-ii", "most-beautiful-item-for-each-query", "maximum-number-of-tasks-you-can-assign"]}, {"contest_title": "\u7b2c 66 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 66", "contest_title_slug": "biweekly-contest-66", "contest_id": 503, "contest_start_time": 1638023400, "contest_duration": 5400, "user_num": 2803, "question_slugs": ["count-common-words-with-one-occurrence", "minimum-number-of-food-buckets-to-feed-the-hamsters", "minimum-cost-homecoming-of-a-robot-in-a-grid", "count-fertile-pyramids-in-a-land"]}, {"contest_title": "\u7b2c 67 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 67", "contest_title_slug": "biweekly-contest-67", "contest_id": 509, "contest_start_time": 1639233000, "contest_duration": 5400, "user_num": 2923, "question_slugs": ["find-subsequence-of-length-k-with-the-largest-sum", "find-good-days-to-rob-the-bank", "detonate-the-maximum-bombs", "sequentially-ordinal-rank-tracker"]}, {"contest_title": "\u7b2c 68 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 68", "contest_title_slug": "biweekly-contest-68", "contest_id": 515, "contest_start_time": 1640442600, "contest_duration": 5400, "user_num": 2854, "question_slugs": ["maximum-number-of-words-found-in-sentences", "find-all-possible-recipes-from-given-supplies", "check-if-a-parentheses-string-can-be-valid", "abbreviating-the-product-of-a-range"]}, {"contest_title": "\u7b2c 69 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 69", "contest_title_slug": "biweekly-contest-69", "contest_id": 521, "contest_start_time": 1641652200, "contest_duration": 5400, "user_num": 3360, "question_slugs": ["capitalize-the-title", "maximum-twin-sum-of-a-linked-list", "longest-palindrome-by-concatenating-two-letter-words", "stamping-the-grid"]}, {"contest_title": "\u7b2c 70 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 70", "contest_title_slug": "biweekly-contest-70", "contest_id": 527, "contest_start_time": 1642861800, "contest_duration": 5400, "user_num": 3640, "question_slugs": ["minimum-cost-of-buying-candies-with-discount", "count-the-hidden-sequences", "k-highest-ranked-items-within-a-price-range", "number-of-ways-to-divide-a-long-corridor"]}, {"contest_title": "\u7b2c 71 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 71", "contest_title_slug": "biweekly-contest-71", "contest_id": 533, "contest_start_time": 1644071400, "contest_duration": 5400, "user_num": 3028, "question_slugs": ["minimum-sum-of-four-digit-number-after-splitting-digits", "partition-array-according-to-given-pivot", "minimum-cost-to-set-cooking-time", "minimum-difference-in-sums-after-removal-of-elements"]}, {"contest_title": "\u7b2c 72 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 72", "contest_title_slug": "biweekly-contest-72", "contest_id": 539, "contest_start_time": 1645281000, "contest_duration": 5400, "user_num": 4400, "question_slugs": ["count-equal-and-divisible-pairs-in-an-array", "find-three-consecutive-integers-that-sum-to-a-given-number", "maximum-split-of-positive-even-integers", "count-good-triplets-in-an-array"]}, {"contest_title": "\u7b2c 73 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 73", "contest_title_slug": "biweekly-contest-73", "contest_id": 545, "contest_start_time": 1646490600, "contest_duration": 5400, "user_num": 5132, "question_slugs": ["most-frequent-number-following-key-in-an-array", "sort-the-jumbled-numbers", "all-ancestors-of-a-node-in-a-directed-acyclic-graph", "minimum-number-of-moves-to-make-palindrome"]}, {"contest_title": "\u7b2c 74 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 74", "contest_title_slug": "biweekly-contest-74", "contest_id": 554, "contest_start_time": 1647700200, "contest_duration": 5400, "user_num": 5442, "question_slugs": ["divide-array-into-equal-pairs", "maximize-number-of-subsequences-in-a-string", "minimum-operations-to-halve-array-sum", "minimum-white-tiles-after-covering-with-carpets"]}, {"contest_title": "\u7b2c 75 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 75", "contest_title_slug": "biweekly-contest-75", "contest_id": 563, "contest_start_time": 1648909800, "contest_duration": 5400, "user_num": 4335, "question_slugs": ["minimum-bit-flips-to-convert-number", "find-triangular-sum-of-an-array", "number-of-ways-to-select-buildings", "sum-of-scores-of-built-strings"]}, {"contest_title": "\u7b2c 76 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 76", "contest_title_slug": "biweekly-contest-76", "contest_id": 572, "contest_start_time": 1650119400, "contest_duration": 5400, "user_num": 4477, "question_slugs": ["find-closest-number-to-zero", "number-of-ways-to-buy-pens-and-pencils", "design-an-atm-machine", "maximum-score-of-a-node-sequence"]}, {"contest_title": "\u7b2c 77 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 77", "contest_title_slug": "biweekly-contest-77", "contest_id": 581, "contest_start_time": 1651329000, "contest_duration": 5400, "user_num": 4211, "question_slugs": ["count-prefixes-of-a-given-string", "minimum-average-difference", "count-unguarded-cells-in-the-grid", "escape-the-spreading-fire"]}, {"contest_title": "\u7b2c 78 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 78", "contest_title_slug": "biweekly-contest-78", "contest_id": 590, "contest_start_time": 1652538600, "contest_duration": 5400, "user_num": 4347, "question_slugs": ["find-the-k-beauty-of-a-number", "number-of-ways-to-split-array", "maximum-white-tiles-covered-by-a-carpet", "substring-with-largest-variance"]}, {"contest_title": "\u7b2c 79 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 79", "contest_title_slug": "biweekly-contest-79", "contest_id": 598, "contest_start_time": 1653748200, "contest_duration": 5400, "user_num": 4250, "question_slugs": ["check-if-number-has-equal-digit-count-and-digit-value", "sender-with-largest-word-count", "maximum-total-importance-of-roads", "booking-concert-tickets-in-groups"]}, {"contest_title": "\u7b2c 80 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 80", "contest_title_slug": "biweekly-contest-80", "contest_id": 608, "contest_start_time": 1654957800, "contest_duration": 5400, "user_num": 3949, "question_slugs": ["strong-password-checker-ii", "successful-pairs-of-spells-and-potions", "match-substring-after-replacement", "count-subarrays-with-score-less-than-k"]}, {"contest_title": "\u7b2c 81 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 81", "contest_title_slug": "biweekly-contest-81", "contest_id": 614, "contest_start_time": 1656167400, "contest_duration": 5400, "user_num": 3847, "question_slugs": ["count-asterisks", "count-unreachable-pairs-of-nodes-in-an-undirected-graph", "maximum-xor-after-operations", "number-of-distinct-roll-sequences"]}, {"contest_title": "\u7b2c 82 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 82", "contest_title_slug": "biweekly-contest-82", "contest_id": 646, "contest_start_time": 1657377000, "contest_duration": 5400, "user_num": 4144, "question_slugs": ["evaluate-boolean-binary-tree", "the-latest-time-to-catch-a-bus", "minimum-sum-of-squared-difference", "subarray-with-elements-greater-than-varying-threshold"]}, {"contest_title": "\u7b2c 83 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 83", "contest_title_slug": "biweekly-contest-83", "contest_id": 652, "contest_start_time": 1658586600, "contest_duration": 5400, "user_num": 4437, "question_slugs": ["best-poker-hand", "number-of-zero-filled-subarrays", "design-a-number-container-system", "shortest-impossible-sequence-of-rolls"]}, {"contest_title": "\u7b2c 84 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 84", "contest_title_slug": "biweekly-contest-84", "contest_id": 658, "contest_start_time": 1659796200, "contest_duration": 5400, "user_num": 4574, "question_slugs": ["merge-similar-items", "count-number-of-bad-pairs", "task-scheduler-ii", "minimum-replacements-to-sort-the-array"]}, {"contest_title": "\u7b2c 85 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 85", "contest_title_slug": "biweekly-contest-85", "contest_id": 668, "contest_start_time": 1661005800, "contest_duration": 5400, "user_num": 4193, "question_slugs": ["minimum-recolors-to-get-k-consecutive-black-blocks", "time-needed-to-rearrange-a-binary-string", "shifting-letters-ii", "maximum-segment-sum-after-removals"]}, {"contest_title": "\u7b2c 86 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 86", "contest_title_slug": "biweekly-contest-86", "contest_id": 688, "contest_start_time": 1662215400, "contest_duration": 5400, "user_num": 4401, "question_slugs": ["find-subarrays-with-equal-sum", "strictly-palindromic-number", "maximum-rows-covered-by-columns", "maximum-number-of-robots-within-budget"]}, {"contest_title": "\u7b2c 87 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 87", "contest_title_slug": "biweekly-contest-87", "contest_id": 703, "contest_start_time": 1663425000, "contest_duration": 5400, "user_num": 4005, "question_slugs": ["count-days-spent-together", "maximum-matching-of-players-with-trainers", "smallest-subarrays-with-maximum-bitwise-or", "minimum-money-required-before-transactions"]}, {"contest_title": "\u7b2c 88 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 88", "contest_title_slug": "biweekly-contest-88", "contest_id": 745, "contest_start_time": 1664634600, "contest_duration": 5400, "user_num": 3905, "question_slugs": ["remove-letter-to-equalize-frequency", "longest-uploaded-prefix", "bitwise-xor-of-all-pairings", "number-of-pairs-satisfying-inequality"]}, {"contest_title": "\u7b2c 89 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 89", "contest_title_slug": "biweekly-contest-89", "contest_id": 755, "contest_start_time": 1665844200, "contest_duration": 5400, "user_num": 3984, "question_slugs": ["number-of-valid-clock-times", "range-product-queries-of-powers", "minimize-maximum-of-array", "create-components-with-same-value"]}, {"contest_title": "\u7b2c 90 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 90", "contest_title_slug": "biweekly-contest-90", "contest_id": 763, "contest_start_time": 1667053800, "contest_duration": 5400, "user_num": 3624, "question_slugs": ["odd-string-difference", "words-within-two-edits-of-dictionary", "destroy-sequential-targets", "next-greater-element-iv"]}, {"contest_title": "\u7b2c 91 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 91", "contest_title_slug": "biweekly-contest-91", "contest_id": 770, "contest_start_time": 1668263400, "contest_duration": 5400, "user_num": 3535, "question_slugs": ["number-of-distinct-averages", "count-ways-to-build-good-strings", "most-profitable-path-in-a-tree", "split-message-based-on-limit"]}, {"contest_title": "\u7b2c 92 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 92", "contest_title_slug": "biweekly-contest-92", "contest_id": 776, "contest_start_time": 1669473000, "contest_duration": 5400, "user_num": 3055, "question_slugs": ["minimum-cuts-to-divide-a-circle", "difference-between-ones-and-zeros-in-row-and-column", "minimum-penalty-for-a-shop", "count-palindromic-subsequences"]}, {"contest_title": "\u7b2c 93 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 93", "contest_title_slug": "biweekly-contest-93", "contest_id": 782, "contest_start_time": 1670682600, "contest_duration": 5400, "user_num": 2929, "question_slugs": ["maximum-value-of-a-string-in-an-array", "maximum-star-sum-of-a-graph", "frog-jump-ii", "minimum-total-cost-to-make-arrays-unequal"]}, {"contest_title": "\u7b2c 94 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 94", "contest_title_slug": "biweekly-contest-94", "contest_id": 789, "contest_start_time": 1671892200, "contest_duration": 5400, "user_num": 2298, "question_slugs": ["maximum-enemy-forts-that-can-be-captured", "reward-top-k-students", "minimize-the-maximum-of-two-arrays", "count-anagrams"]}, {"contest_title": "\u7b2c 95 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 95", "contest_title_slug": "biweekly-contest-95", "contest_id": 798, "contest_start_time": 1673101800, "contest_duration": 5400, "user_num": 2880, "question_slugs": ["categorize-box-according-to-criteria", "find-consecutive-integers-from-a-data-stream", "find-xor-beauty-of-array", "maximize-the-minimum-powered-city"]}, {"contest_title": "\u7b2c 96 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 96", "contest_title_slug": "biweekly-contest-96", "contest_id": 804, "contest_start_time": 1674311400, "contest_duration": 5400, "user_num": 2103, "question_slugs": ["minimum-common-value", "minimum-operations-to-make-array-equal-ii", "maximum-subsequence-score", "check-if-point-is-reachable"]}, {"contest_title": "\u7b2c 97 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 97", "contest_title_slug": "biweekly-contest-97", "contest_id": 810, "contest_start_time": 1675521000, "contest_duration": 5400, "user_num": 2631, "question_slugs": ["separate-the-digits-in-an-array", "maximum-number-of-integers-to-choose-from-a-range-i", "maximize-win-from-two-segments", "disconnect-path-in-a-binary-matrix-by-at-most-one-flip"]}, {"contest_title": "\u7b2c 98 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 98", "contest_title_slug": "biweekly-contest-98", "contest_id": 816, "contest_start_time": 1676730600, "contest_duration": 5400, "user_num": 3250, "question_slugs": ["maximum-difference-by-remapping-a-digit", "minimum-score-by-changing-two-elements", "minimum-impossible-or", "handling-sum-queries-after-update"]}, {"contest_title": "\u7b2c 99 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 99", "contest_title_slug": "biweekly-contest-99", "contest_id": 822, "contest_start_time": 1677940200, "contest_duration": 5400, "user_num": 3467, "question_slugs": ["split-with-minimum-sum", "count-total-number-of-colored-cells", "count-ways-to-group-overlapping-ranges", "count-number-of-possible-root-nodes"]}, {"contest_title": "\u7b2c 100 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 100", "contest_title_slug": "biweekly-contest-100", "contest_id": 832, "contest_start_time": 1679149800, "contest_duration": 5400, "user_num": 3639, "question_slugs": ["distribute-money-to-maximum-children", "maximize-greatness-of-an-array", "find-score-of-an-array-after-marking-all-elements", "minimum-time-to-repair-cars"]}, {"contest_title": "\u7b2c 101 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 101", "contest_title_slug": "biweekly-contest-101", "contest_id": 842, "contest_start_time": 1680359400, "contest_duration": 5400, "user_num": 3353, "question_slugs": ["form-smallest-number-from-two-digit-arrays", "find-the-substring-with-maximum-cost", "make-k-subarray-sums-equal", "shortest-cycle-in-a-graph"]}, {"contest_title": "\u7b2c 102 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 102", "contest_title_slug": "biweekly-contest-102", "contest_id": 853, "contest_start_time": 1681569000, "contest_duration": 5400, "user_num": 3058, "question_slugs": ["find-the-width-of-columns-of-a-grid", "find-the-score-of-all-prefixes-of-an-array", "cousins-in-binary-tree-ii", "design-graph-with-shortest-path-calculator"]}, {"contest_title": "\u7b2c 103 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 103", "contest_title_slug": "biweekly-contest-103", "contest_id": 859, "contest_start_time": 1682778600, "contest_duration": 5400, "user_num": 2299, "question_slugs": ["maximum-sum-with-exactly-k-elements", "find-the-prefix-common-array-of-two-arrays", "maximum-number-of-fish-in-a-grid", "make-array-empty"]}, {"contest_title": "\u7b2c 104 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 104", "contest_title_slug": "biweekly-contest-104", "contest_id": 866, "contest_start_time": 1683988200, "contest_duration": 5400, "user_num": 2519, "question_slugs": ["number-of-senior-citizens", "sum-in-a-matrix", "maximum-or", "power-of-heroes"]}, {"contest_title": "\u7b2c 105 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 105", "contest_title_slug": "biweekly-contest-105", "contest_id": 873, "contest_start_time": 1685197800, "contest_duration": 5400, "user_num": 2604, "question_slugs": ["buy-two-chocolates", "extra-characters-in-a-string", "maximum-strength-of-a-group", "greatest-common-divisor-traversal"]}, {"contest_title": "\u7b2c 106 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 106", "contest_title_slug": "biweekly-contest-106", "contest_id": 879, "contest_start_time": 1686407400, "contest_duration": 5400, "user_num": 2346, "question_slugs": ["check-if-the-number-is-fascinating", "find-the-longest-semi-repetitive-substring", "movement-of-robots", "find-a-good-subset-of-the-matrix"]}, {"contest_title": "\u7b2c 107 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 107", "contest_title_slug": "biweekly-contest-107", "contest_id": 885, "contest_start_time": 1687617000, "contest_duration": 5400, "user_num": 1870, "question_slugs": ["find-maximum-number-of-string-pairs", "construct-the-longest-new-string", "decremental-string-concatenation", "count-zero-request-servers"]}, {"contest_title": "\u7b2c 108 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 108", "contest_title_slug": "biweekly-contest-108", "contest_id": 891, "contest_start_time": 1688826600, "contest_duration": 5400, "user_num": 2349, "question_slugs": ["longest-alternating-subarray", "relocate-marbles", "partition-string-into-minimum-beautiful-substrings", "number-of-black-blocks"]}, {"contest_title": "\u7b2c 109 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 109", "contest_title_slug": "biweekly-contest-109", "contest_id": 897, "contest_start_time": 1690036200, "contest_duration": 5400, "user_num": 2461, "question_slugs": ["check-if-array-is-good", "sort-vowels-in-a-string", "visit-array-positions-to-maximize-score", "ways-to-express-an-integer-as-sum-of-powers"]}, {"contest_title": "\u7b2c 110 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 110", "contest_title_slug": "biweekly-contest-110", "contest_id": 903, "contest_start_time": 1691245800, "contest_duration": 5400, "user_num": 2546, "question_slugs": ["account-balance-after-rounded-purchase", "insert-greatest-common-divisors-in-linked-list", "minimum-seconds-to-equalize-a-circular-array", "minimum-time-to-make-array-sum-at-most-x"]}, {"contest_title": "\u7b2c 111 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 111", "contest_title_slug": "biweekly-contest-111", "contest_id": 909, "contest_start_time": 1692455400, "contest_duration": 5400, "user_num": 2787, "question_slugs": ["count-pairs-whose-sum-is-less-than-target", "make-string-a-subsequence-using-cyclic-increments", "sorting-three-groups", "number-of-beautiful-integers-in-the-range"]}, {"contest_title": "\u7b2c 112 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 112", "contest_title_slug": "biweekly-contest-112", "contest_id": 917, "contest_start_time": 1693665000, "contest_duration": 5400, "user_num": 2900, "question_slugs": ["check-if-strings-can-be-made-equal-with-operations-i", "check-if-strings-can-be-made-equal-with-operations-ii", "maximum-sum-of-almost-unique-subarray", "count-k-subsequences-of-a-string-with-maximum-beauty"]}, {"contest_title": "\u7b2c 113 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 113", "contest_title_slug": "biweekly-contest-113", "contest_id": 923, "contest_start_time": 1694874600, "contest_duration": 5400, "user_num": 3028, "question_slugs": ["minimum-right-shifts-to-sort-the-array", "minimum-array-length-after-pair-removals", "count-pairs-of-points-with-distance-k", "minimum-edge-reversals-so-every-node-is-reachable"]}, {"contest_title": "\u7b2c 114 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 114", "contest_title_slug": "biweekly-contest-114", "contest_id": 929, "contest_start_time": 1696084200, "contest_duration": 5400, "user_num": 2406, "question_slugs": ["minimum-operations-to-collect-elements", "minimum-number-of-operations-to-make-array-empty", "split-array-into-maximum-number-of-subarrays", "maximum-number-of-k-divisible-components"]}, {"contest_title": "\u7b2c 115 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 115", "contest_title_slug": "biweekly-contest-115", "contest_id": 935, "contest_start_time": 1697293800, "contest_duration": 5400, "user_num": 2809, "question_slugs": ["last-visited-integers", "longest-unequal-adjacent-groups-subsequence-i", "longest-unequal-adjacent-groups-subsequence-ii", "count-of-sub-multisets-with-bounded-sum"]}, {"contest_title": "\u7b2c 116 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 116", "contest_title_slug": "biweekly-contest-116", "contest_id": 941, "contest_start_time": 1698503400, "contest_duration": 5400, "user_num": 2904, "question_slugs": ["subarrays-distinct-element-sum-of-squares-i", "minimum-number-of-changes-to-make-binary-string-beautiful", "length-of-the-longest-subsequence-that-sums-to-target", "subarrays-distinct-element-sum-of-squares-ii"]}, {"contest_title": "\u7b2c 117 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 117", "contest_title_slug": "biweekly-contest-117", "contest_id": 949, "contest_start_time": 1699713000, "contest_duration": 5400, "user_num": 2629, "question_slugs": ["distribute-candies-among-children-i", "distribute-candies-among-children-ii", "number-of-strings-which-can-be-rearranged-to-contain-substring", "maximum-spending-after-buying-items"]}, {"contest_title": "\u7b2c 118 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 118", "contest_title_slug": "biweekly-contest-118", "contest_id": 955, "contest_start_time": 1700922600, "contest_duration": 5400, "user_num": 2425, "question_slugs": ["find-words-containing-character", "maximize-area-of-square-hole-in-grid", "minimum-number-of-coins-for-fruits", "find-maximum-non-decreasing-array-length"]}, {"contest_title": "\u7b2c 119 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 119", "contest_title_slug": "biweekly-contest-119", "contest_id": 961, "contest_start_time": 1702132200, "contest_duration": 5400, "user_num": 2472, "question_slugs": ["find-common-elements-between-two-arrays", "remove-adjacent-almost-equal-characters", "length-of-longest-subarray-with-at-most-k-frequency", "number-of-possible-sets-of-closing-branches"]}, {"contest_title": "\u7b2c 120 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 120", "contest_title_slug": "biweekly-contest-120", "contest_id": 967, "contest_start_time": 1703341800, "contest_duration": 5400, "user_num": 2542, "question_slugs": ["count-the-number-of-incremovable-subarrays-i", "find-polygon-with-the-largest-perimeter", "count-the-number-of-incremovable-subarrays-ii", "find-number-of-coins-to-place-in-tree-nodes"]}, {"contest_title": "\u7b2c 121 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 121", "contest_title_slug": "biweekly-contest-121", "contest_id": 973, "contest_start_time": 1704551400, "contest_duration": 5400, "user_num": 2218, "question_slugs": ["smallest-missing-integer-greater-than-sequential-prefix-sum", "minimum-number-of-operations-to-make-array-xor-equal-to-k", "minimum-number-of-operations-to-make-x-and-y-equal", "count-the-number-of-powerful-integers"]}, {"contest_title": "\u7b2c 122 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 122", "contest_title_slug": "biweekly-contest-122", "contest_id": 979, "contest_start_time": 1705761000, "contest_duration": 5400, "user_num": 2547, "question_slugs": ["divide-an-array-into-subarrays-with-minimum-cost-i", "find-if-array-can-be-sorted", "minimize-length-of-array-using-operations", "divide-an-array-into-subarrays-with-minimum-cost-ii"]}, {"contest_title": "\u7b2c 123 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 123", "contest_title_slug": "biweekly-contest-123", "contest_id": 985, "contest_start_time": 1706970600, "contest_duration": 5400, "user_num": 2209, "question_slugs": ["type-of-triangle", "find-the-number-of-ways-to-place-people-i", "maximum-good-subarray-sum", "find-the-number-of-ways-to-place-people-ii"]}, {"contest_title": "\u7b2c 124 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 124", "contest_title_slug": "biweekly-contest-124", "contest_id": 991, "contest_start_time": 1708180200, "contest_duration": 5400, "user_num": 1861, "question_slugs": ["maximum-number-of-operations-with-the-same-score-i", "apply-operations-to-make-string-empty", "maximum-number-of-operations-with-the-same-score-ii", "maximize-consecutive-elements-in-an-array-after-modification"]}, {"contest_title": "\u7b2c 125 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 125", "contest_title_slug": "biweekly-contest-125", "contest_id": 997, "contest_start_time": 1709389800, "contest_duration": 5400, "user_num": 2599, "question_slugs": ["minimum-operations-to-exceed-threshold-value-i", "minimum-operations-to-exceed-threshold-value-ii", "count-pairs-of-connectable-servers-in-a-weighted-tree-network", "find-the-maximum-sum-of-node-values"]}, {"contest_title": "\u7b2c 126 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 126", "contest_title_slug": "biweekly-contest-126", "contest_id": 1003, "contest_start_time": 1710599400, "contest_duration": 5400, "user_num": 3234, "question_slugs": ["find-the-sum-of-encrypted-integers", "mark-elements-on-array-by-performing-queries", "replace-question-marks-in-string-to-minimize-its-value", "find-the-sum-of-the-power-of-all-subsequences"]}, {"contest_title": "\u7b2c 127 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 127", "contest_title_slug": "biweekly-contest-127", "contest_id": 1010, "contest_start_time": 1711809000, "contest_duration": 5400, "user_num": 2951, "question_slugs": ["shortest-subarray-with-or-at-least-k-i", "minimum-levels-to-gain-more-points", "shortest-subarray-with-or-at-least-k-ii", "find-the-sum-of-subsequence-powers"]}, {"contest_title": "\u7b2c 128 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 128", "contest_title_slug": "biweekly-contest-128", "contest_id": 1017, "contest_start_time": 1713018600, "contest_duration": 5400, "user_num": 2654, "question_slugs": ["score-of-a-string", "minimum-rectangles-to-cover-points", "minimum-time-to-visit-disappearing-nodes", "find-the-number-of-subarrays-where-boundary-elements-are-maximum"]}, {"contest_title": "\u7b2c 129 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 129", "contest_title_slug": "biweekly-contest-129", "contest_id": 1023, "contest_start_time": 1714228200, "contest_duration": 5400, "user_num": 2511, "question_slugs": ["make-a-square-with-the-same-color", "right-triangles", "find-all-possible-stable-binary-arrays-i", "find-all-possible-stable-binary-arrays-ii"]}, {"contest_title": "\u7b2c 130 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 130", "contest_title_slug": "biweekly-contest-130", "contest_id": 1029, "contest_start_time": 1715437800, "contest_duration": 5400, "user_num": 2604, "question_slugs": ["check-if-grid-satisfies-conditions", "maximum-points-inside-the-square", "minimum-substring-partition-of-equal-character-frequency", "find-products-of-elements-of-big-array"]}, {"contest_title": "\u7b2c 131 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 131", "contest_title_slug": "biweekly-contest-131", "contest_id": 1035, "contest_start_time": 1716647400, "contest_duration": 5400, "user_num": 2537, "question_slugs": ["find-the-xor-of-numbers-which-appear-twice", "find-occurrences-of-an-element-in-an-array", "find-the-number-of-distinct-colors-among-the-balls", "block-placement-queries"]}, {"contest_title": "\u7b2c 132 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 132", "contest_title_slug": "biweekly-contest-132", "contest_id": 1042, "contest_start_time": 1717857000, "contest_duration": 5400, "user_num": 2457, "question_slugs": ["clear-digits", "find-the-first-player-to-win-k-games-in-a-row", "find-the-maximum-length-of-a-good-subsequence-i", "find-the-maximum-length-of-a-good-subsequence-ii"]}, {"contest_title": "\u7b2c 133 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 133", "contest_title_slug": "biweekly-contest-133", "contest_id": 1048, "contest_start_time": 1719066600, "contest_duration": 5400, "user_num": 2326, "question_slugs": ["find-minimum-operations-to-make-all-elements-divisible-by-three", "minimum-operations-to-make-binary-array-elements-equal-to-one-i", "minimum-operations-to-make-binary-array-elements-equal-to-one-ii", "count-the-number-of-inversions"]}, {"contest_title": "\u7b2c 134 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 134", "contest_title_slug": "biweekly-contest-134", "contest_id": 1055, "contest_start_time": 1720276200, "contest_duration": 5400, "user_num": 2411, "question_slugs": ["alternating-groups-i", "maximum-points-after-enemy-battles", "alternating-groups-ii", "number-of-subarrays-with-and-value-of-k"]}, {"contest_title": "\u7b2c 135 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 135", "contest_title_slug": "biweekly-contest-135", "contest_id": 1061, "contest_start_time": 1721485800, "contest_duration": 5400, "user_num": 2260, "question_slugs": ["find-the-winning-player-in-coin-game", "minimum-length-of-string-after-operations", "minimum-array-changes-to-make-differences-equal", "maximum-score-from-grid-operations"]}, {"contest_title": "\u7b2c 136 \u573a\u53cc\u5468\u8d5b", "contest_title_en": "Biweekly Contest 136", "contest_title_slug": "biweekly-contest-136", "contest_id": 1068, "contest_start_time": 1722695400, "contest_duration": 5400, "user_num": 2418, "question_slugs": ["find-the-number-of-winning-players", "minimum-number-of-flips-to-make-binary-grid-palindromic-i", "minimum-number-of-flips-to-make-binary-grid-palindromic-ii", "time-taken-to-mark-all-nodes"]}, {"contest_title": "\u7b2c 410 \u573a\u5468\u8d5b", "contest_title_en": "Weekly Contest 410", "contest_title_slug": "weekly-contest-410", "contest_id": 1075, "contest_start_time": 1723343400, "contest_duration": 5400, "user_num": 2987, "question_slugs": ["snake-in-matrix", "count-the-number-of-good-nodes", "find-the-count-of-monotonic-pairs-i", "find-the-count-of-monotonic-pairs-ii"]}] \ No newline at end of file