-
|
Can anyone provide links or examples of solving a minimum time problem using InfiniteOpt.jl? |
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 6 replies
-
|
Hi there! Welcome to the InfiniteOpt discussion forum! Minimum time problems can be reformulated into a standard optimal control problem. A nice video tutorial is given here in the context of an optimal rocket launch problem where we want to minimize the final time for the rocket to arrive. The key reformulation trick is to scale the total time by the final time with The script below implements the same rocket example in InfiniteOpt: using InfiniteOpt, Ipopt, Plots
# Define the model
model = InfiniteModel(Ipopt.Optimizer)
# Setup up the normalized time parameter τ = t / tf
@infinite_parameter(model, τ in [0, 1], num_supports = 101)
# Create the variables
@variable(model, -1.1 <= u <= 1.1, Infinite(τ), start = 0)
@variable(model, s, Infinite(τ), start = 0)
@variable(model, 0 <= v <= 1.7, Infinite(τ), start = 0)
@variable(model, m >= 0.2, Infinite(τ), start = 1)
@variable(model, 0.1 <= tf <= 100, start = 1)
# Set the objective
@objective(model, Min, tf)
# Define the ODEs
@constraint(model, ∂(s, τ) == tf * v)
@constraint(model, m * ∂(v, τ) == tf * (u - 0.2 * v^2))
@constraint(model, ∂(m, τ) == tf * (-0.01 * u^2))
# Set the initial conditions
@constraint(model, s(0) == 0)
@constraint(model, v(0) == 0)
@constraint(model, m(0) == 1)
# Set terminal constraints
@constraint(model, s(1) == 10)
@constraint(model, v(1) == 0)
# Optimize and get the results
optimize!(model)
opt_u = value(u)
opt_s = value(s)
opt_m = value(m)
opt_v = value(v)
opt_tf = value(tf)
# Get the scaled times
ts = value(τ) * opt_tf
# Plot the optimal trajectories
plot(ts, [opt_s opt_v opt_m opt_u], layout = (4, 1), legend = false,
xlabel = "Time", ylabel = ["Position" "Velocity" "Mass" "Force"],
xlims = (0, opt_tf)) |
Beta Was this translation helpful? Give feedback.
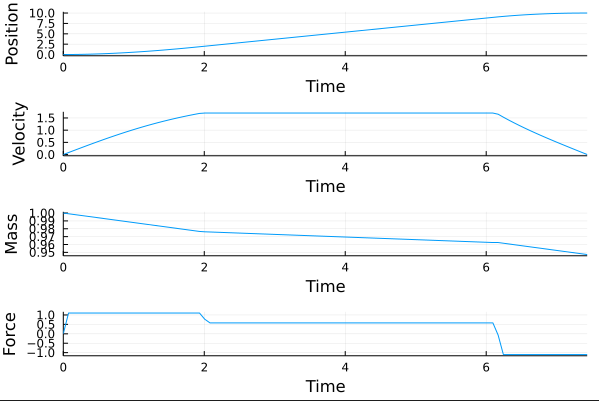
Hi there! Welcome to the InfiniteOpt discussion forum!
Minimum time problems can be reformulated into a standard optimal control problem. A nice video tutorial is given here in the context of an optimal rocket launch problem where we want to minimize the final time for the rocket to arrive.
The key reformulation trick is to scale the total time by the final time with
τ = t / tfand lettfbe a finite variable.The script below implements the same rocket example in InfiniteOpt: