Minimum time objective ensuring waypoints touched in hovercraft example

[CurioMath]

Inspiring from the discussion on minimum time problems I have tried a hand on hovercraft example in the documentation with minimum time objective, while ensuring that the hovercraft hits all waypoints. But not sure how to specify the constraint for the waypoints, since I don't want to specify the time to reach at each point. The hovercraft must reach back to initial position in minimum time while traversing through the specified waypoints at any point of time.
Can I get any possible help to do this?
Thanks in advance..

[IlyaOrson]

If you know the order of the waypoints maybe you could split the problem into one minimum time problem per waypoint thanks to the principle of optimality.

[pulsipher]

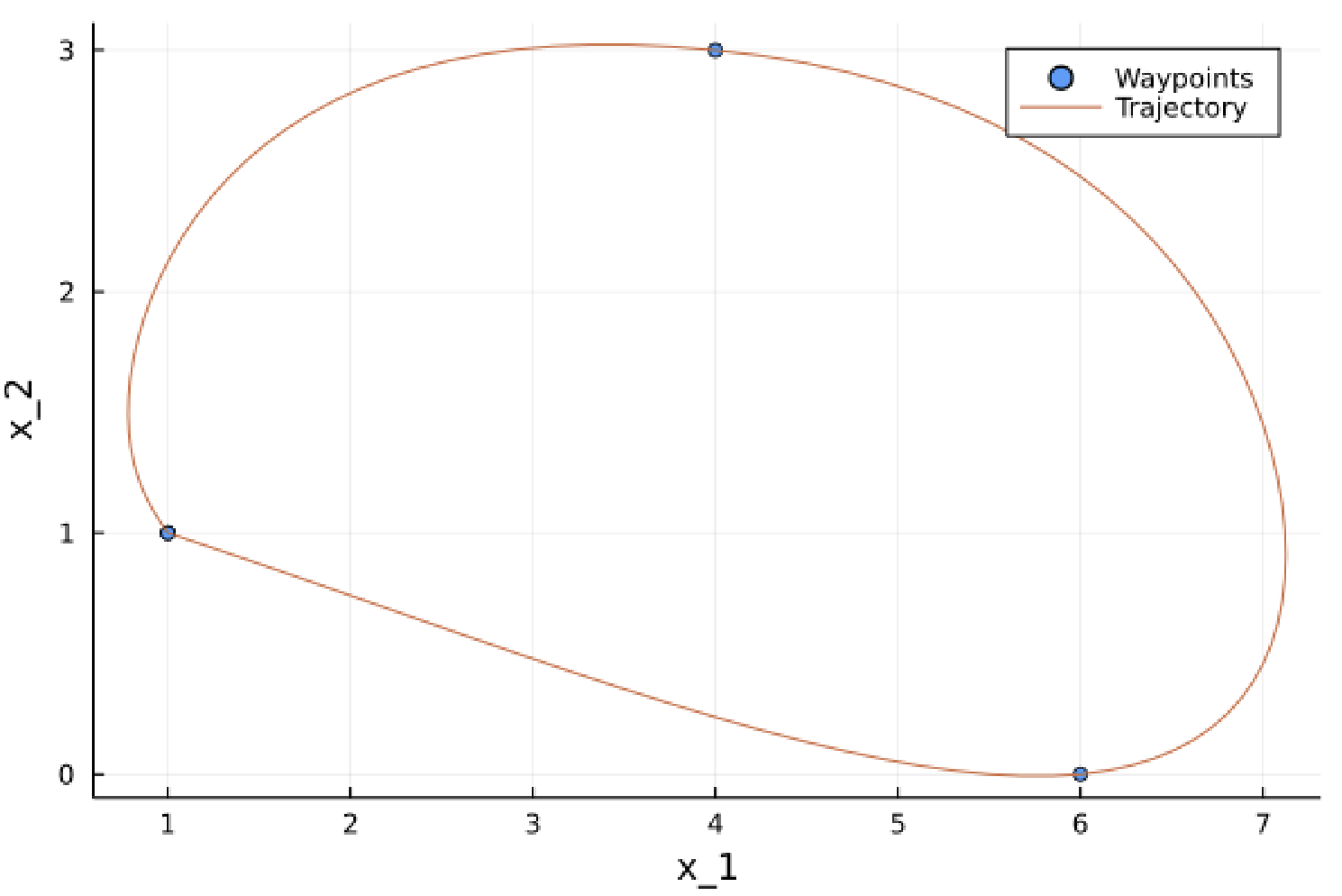
Hi @CurioMath, welcome to the forum!

This is a good and surprisingly challenging question. The short answer (to my knowledge) is that formulating/solving minimum time waypoint problems (i.e., minimum time path-planning problems) is an open research question. There is a lot of literature of various approaches that have been proposed for this in the context of autonomous vehicles (e.g., cars, UAVs, submersibles. etc.) that employ various simplifying assumptions. Admittedly, I am not an expert in this particular research area. Work from the Automatic Control Lab at ETH Zurich and the Borrelli group at UC-Berkeley may be of interest.

One simple way to approach this would be to do what @IlyaOrson suggests as decompose this into (n-1) sub-problems treat each sequential pair of waypoints as a traditional minimum time problem. The cost of this approach is that the overall solution is likely to be sub-optimal since the final state of one sub-problem may lead to a sub-optimal starting condition of the next sub-problem. However, this could then inspire some sort of smart update routine to converge to the optimal solution (which is an interesting research idea).

Another simple approach would be to adapt the minimum time problem to consider waypoints at certain scaled times. This of course is more restrictive then allowing the waypoints to be reached at anytime, hence, this approach is sub-optimal relative to the full problem. For the sake of example, the script below employs this simple approach.

using InfiniteOpt, Ipopt, Plots

# Define the parameters 
xw = [1 4 6 1; 1 3 0 1] # positions
tw = [0, 0.4, 0.8, 1]   # scaled times

# Define the model
m = InfiniteModel(Ipopt.Optimizer)

# Define the scaled time
@infinite_parameter(m, τ ∈ [0, 1], num_supports = 101)

# Add the variables
@variables(m, begin
    # state variables
    x[1:2], Infinite(τ)
    v[1:2], Infinite(τ)
    # control variables
    -1 <= u[1:2] <= 1, Infinite(τ), (start = 0) # enforce control limits
    0 <= tf <= 500, (start = 60)
end)

# Set the objective
@objective(m, Min, tf)

# Set the constraints
@constraint(m, [i = 1:2], v[i](0) == 0)
@constraint(m, [i = 1:2], ∂(x[i], τ) == tf * v[i])
@constraint(m, [i = 1:2], ∂(v[i], τ) == tf * u[i])
@constraint(m, [i = 1:2, j = eachindex(tw)], x[i](tw[j]) == xw[i, j])

# Solve and get the results
optimize!(m)
opt_tf = value(tf)
opt_x = value.(x)
opt_u = value.(u)

# Plot the results
scatter(xw[1,:], xw[2,:], label = "Waypoints")
plot!(opt_x[1], opt_x[2], label = "Trajectory")
xlabel!("x_1")
ylabel!("x_2")

Which obtains an optimal time of 10 seconds. Note we need to add bounds on the thrust u to make this a well-posed bounded problem.

[CurioMath]

Great thanks for the aforementioned approaches on this problem. Let me see the suboptimal solution by decomposing original problem into subproblems taking waypoints in pairs. I just want to look forward beyond the restrictive approach using scaled timepoints. I think it's interesting to dig deep into more literature behind this. Anyway thanks for all the insights...

[pulsipher]

See #219 for a continuation on this discussion.