Fastest way to compute Empirical Fisher Information Matrix Vector product? #10004
Replies: 1 comment 5 replies
-
|
Hey, what you do is I believe quite efficient. I do something similar. However, instead of doing Hence the pullback I implement it as this (I don't use from typing import Callable, Any, Tuple
from chex import Array, ArrayTree
from jax import vmap, jvp, vjp
def efvp(
negative_log_likelihood: Callable[[Array, Array], float], # (outputs, targets) -> (loss)
model_fun: Callable[[ArrayTree, Array], Array], # (params, inputs) -> (outputs)
primals: Any,
tangents: Any,
data: Tuple[ArrayTree, ArrayTree], # D = (x, y) pairs.
has_aux: bool = False
) -> Tuple[Any, ...]:
# Ensure that batch-dimensions are independent of one-another during autodiff.
negative_log_likelihood = vmap(negative_log_likelihood, in_axes=(0, 0))
# Compose the model and loss function; the antiderivative of the score function.
x, y = data
param_loss = lambda p: negative_log_likelihood(model_fun(p, x), y)
return _core_efvp(param_loss, primals, tangents, has_aux)
def _core_efvp(
param_loss: Callable,
primals: Any,
tangents: Any,
has_aux: bool = False,
) -> Tuple[Any, ...]:
y, Jt, *aux = jvp(param_loss, primals, tangents, has_aux=has_aux)
pullback = vjp(param_loss, *primals, has_aux=has_aux)[1]
if has_aux:
return y, pullback(Jt), aux
return y, pullback(Jt)By the way, if you want to do Natural Gradient descent, the Empirical Fisher may not be the best choice to precondition on. If your model parameterizes an exponential family distribution, you could use the GGN as an alternative, or simply approximate the Fisher conditional on |
Beta Was this translation helpful? Give feedback.
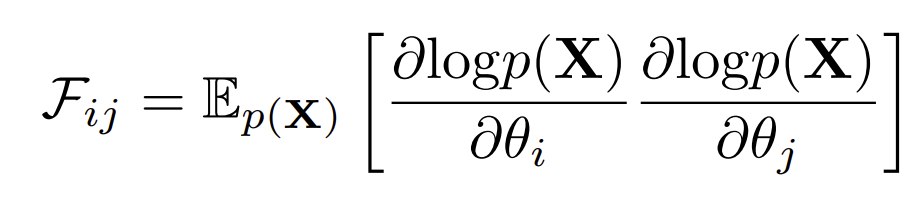
Uh oh!
There was an error while loading. Please reload this page.
Uh oh!
There was an error while loading. Please reload this page.
-
My draft:
Intention: Using conjugate gradient descent to solve
FΔθ=dL/dθfor natural gradient descent.Fis Fisher Information Matrix, i.e. Expectation(overx) of self outer product of∇_θ(log_p(x)).Beta Was this translation helpful? Give feedback.
All reactions