A grad on an integration method leads to NaN... Why?
#10211
Replies: 2 comments 1 reply
-
|
I did some debugging: using def f(x):
return jnp.sqrt(jnp.linspace(0, x, 5))
jax.jacrev(f)(1.0)
# DeviceArray([nan, nan, nan, nan, nan], dtype=float32, weak_type=True)Narrowing it down more, the issue seems to come from the first value in the def f(x):
return jnp.sqrt(x * 0.0)
jax.grad(f)(1.0) # NaNSymbolically, the derivative of So it looks like the issue is with your particular intf5 = lambda x: jax_simps(f5,1E-7,x,N=2**10) |
Beta Was this translation helpful? Give feedback.
-
|
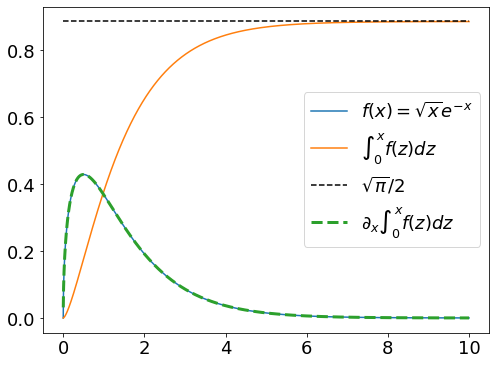
Ho I just realize something that explain the NaN. Here is the explanation. Remember that Simpson integration can be written as with So, when differentiating wrt But in case if So the trick is to avoid the singularity: intf5 = lambda x: jax_simps(f5,1e-7,x,N=2**10)
grad(intf5)(1.0)now gives |
Beta Was this translation helpful? Give feedback.
Uh oh!
There was an error while loading. Please reload this page.
-
Hello,
Here is a simple Simpson integration routine:
It works quite well and for instance
gives
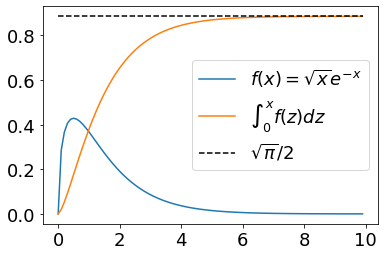
As an exercise I would like to show that
but
Any help would be welcome. Thanks
Beta Was this translation helpful? Give feedback.
All reactions