Why is JAX so fast? #11078
Why is JAX so fast?
#11078
-
|
I was writing a notebook to illustrate the performance trade-offs of array-oriented programming and imperative programming, which calculates the Mandelbrot set in a variety of different ways:
The reason I chose the Mandelbrot set is because each pixel can be calculated independently, but the algorithm that determines the value of each pixel must "iterate until converged," which can be a different number of times for different pixels. Then it occurred to me to add JAX, because it's an independent basis vector in this space:
The details are all in the linked notebook (above), but here's the bottom line:
I had a pretty good story going until JAX was added to the mix. That story was:
So we basically have 3 levels: the best a GPU can do, the best a CPU can do, and Python. CuPy and NumPy with temporary arrays are somewhat worse than the best a GPU or a CPU can do, respectively. Nice story. But then I added JAX, and its final CPU speed is almost 5× better than all of the compiled CPU variants (and those are pretty close to each other), and its final GPU speed is about 6× better than CuPy and Numba-CUDA. How can that be? At first, I noticed that the CPU version was using all my cores, whereas the other tests were single-threaded. There isn't a good way to turn that off, so I forced the whole JupyterLab process to have affinity with CPU 0: taskset -c 0 jupyter labNot only did I see in assert len(jax.devices("cpu")) == 1in the code to make sure it's not accidentally run on all cores in the future. Then I noticed that JAX asynchronously dispatches its tasks, so I put a It used to be the case that the maximum number of iterations in the algorithm was variable, but JAX won't compile with that (since it's a tracer). So I made all the implementations use a compile-time constant maximum number of iterations, just to be fair. Thinking that JAX was taking advantage of that to unroll the loop over iterations, I expected C++ ( What gives? Is my test still unfair because of something I didn't think of? Or if JAX really is much faster for this kind of algorithm, why? What is XLA doing differently from gcc, LLVM, nvrtc, and NVVM that makes it so much faster? Below are some details, in case the answer is hidden in them. `/proc/cpuinfo` for CPU 0 (the one I pinned the whole JupyterLab process to)`sudo lshw -C display` for the GPU (and also the built-in graphics)`nvidia-smi -a` for the GPULLVM for `numba_inner_loop`, which has a low-level function and also a much larger unboxing/boxing functionx86 assembly for `numba_inner_loop`, which has a low-level function and also a much larger unboxing/boxing functionLLVM for `one_pixel_numba_cuda`, which is just the low-level functionPTX for `one_pixel_numba_cuda`, which is just the low-level functionOn the plus side, if there's a good reason why JAX is much faster for this type of algorithm, my Mandelbrot study becomes a great advertisement for JAX, XLA, or both! (Especially since the example was not hand-selected for it.) |
Beta Was this translation helpful? Give feedback.
Answered by
YouJiacheng
Jun 13, 2022
Replies: 14 comments 42 replies
-
|
To force jax to use a single CPU you can try to set this flag: XLA_FLAGS="--xla_force_host_platform_device_count=1"and do a |
Beta Was this translation helpful? Give feedback.
1 reply
-
|
I did force it onto one thread by setting the CPU affinity of the whole JupyterLab process to one core (number 0, just to pick one). Both this method and setting environment variables require changes to be made before starting the process, but I found What's a batch axis? Could the speed I'm seeing be due to a stream that executes code while moving data? The competitors' numbers are all based on creating an array as a first step, performing the computation, and (if it's on the GPU) pulling out back to the CPU as a third step. But the difference between copying the JAX array back from the GPU vs leaving it there is the 3 ms I quoted above vs 0.5 ms. The competitor GPU numbers are 22 ms and 24 ms. Those are different orders or magnitude—I don't see how a fancier way of moving data can account for that much difference. |
Beta Was this translation helpful? Give feedback.
-
IIUC, JAX tracers have static shape, thus |
Beta Was this translation helpful? Give feedback.
1 reply
-
I made I had another thought that I'd have to check later when I can get to the same machine that did these tests: all of the non-JAX implementations that "run at top speed" (have imperative code per-pixel) have a
Compile time is taken out by the fact that, in the notebook, each implementation is used to create a plot of the Mandelbrot before going into the |
Beta Was this translation helpful? Give feedback.
-
|
BTW, for "CuPy with a custom kernel", it seems that warp divergence also prevent global memory access coalescing? |
Beta Was this translation helpful? Give feedback.
4 replies
-
Would JAX/XLA automatically configure it to do that? The hand-written CUDA code, both in C++ and Numba, is quite explicit about which CUDA threads get to work on which pixels, but if the I'm confused about what you mean by "global memory access coalescing," but I think if I rewrite the non-JAX implementations to not
That would easily be large enough for the factor of 6 seen in GPUs. (So maybe it's "as much as 16×, but in practice only 6×".) |
Beta Was this translation helpful? Give feedback.
-
|
By "global memory access coalescing", I mean CUDA global memory access uses 32B sector, and will coalesce memory access in a warp, i.e. if >1 threads in a warp access 1 sector at the same time, only 1 DRAM access is performed for this sector. E.g. if 32 threads in a warp access (aligned) contiguous |
Beta Was this translation helpful? Give feedback.
-
|
Ah, you mean like "cache lines" in CPU memory access, in which data are sent from RAM to the CPU in aligned, contiguous chunks of about 64 bytes—you mean that GPU processing units have something similar when accessing global memory, and I'm using it badly:
So I'm accessing the 2D array in column major order when I want row major order or vice-versa? I'm going to add that to my checklist of things to toggle. |
Beta Was this translation helpful? Give feedback.
-
|
Yes. Just like "cache lines" in CPU. GPU chunks is of 32 Bytes. I believe XLA will take care of this. |
Beta Was this translation helpful? Give feedback.
-
|
One important thing: JAX use complex64(float32 for each part) instead of complex128 by default, did you take care of it? |
Beta Was this translation helpful? Give feedback.
1 reply
-
You're right, that is different: the non-JAX implementations used There could also be different libraries for handling complex numbers. I saw a big difference between Okay, I have some things to try for standardizing the complex number handling, starting with bit width. Thanks! |
Beta Was this translation helpful? Give feedback.
-
|
Summarizing the above, my current to-do list of things to check:
If these things explain the difference, it still comes out as a win for the JAX/XLA approach because these optimizations are hard to do manually. You'll have won a convert, and I'm trying to see how my project might fit into a world in which array bounds are all known at compile-time. (For my project in full generality, it would be hard.) |
Beta Was this translation helpful? Give feedback.
4 replies
-
|
Note: For "memory coalescing"(or "coalesced memory access", I might use an inexact terminology before) you should exchange the cupy_custom_kernel = cp.RawKernel("""
#include <cupy/complex.cuh>
extern "C" __global__
void cupy_custom_kernel(int height, int width, int* fractal) {
int y = blockIdx.x * blockDim.x + threadIdx.x;
int x = blockIdx.y * blockDim.y + threadIdx.y;
complex<double> j(0.0, 1.0);
complex<double> z, c;
z = c = complex<double>(-1.5 + y*1.0/(height + 1)) - j + complex<double>(x*1.5)*j/complex<double>(width + 1);
int r = 20;
#pragma unroll
for (int i = 0; i < 20; i++) {
z = z * z + c;
r = (z.real() * z.imag() > 4 && r == 20) ? i : r;
}
fractal[x*width + y] = r;
}
""", "cupy_custom_kernel")
def run_cupy_custom_kernel(height, width):
fractal = cp.empty((height, width), dtype=np.int32)
griddim = (math.ceil(width/ 32), math.ceil(height / 32))
blockdim = (32, 32)
cupy_custom_kernel(griddim, blockdim, (height, width, fractal))
return fractal.get() |
Beta Was this translation helpful? Give feedback.
-
Good point; I was going to make the size a multiple of block size to be able to avoid that issue. Somehow, I didn't overwrite any array bounds. |
Beta Was this translation helpful? Give feedback.
-
|
I updated my snippet and I think it should be faster. |
Beta Was this translation helpful? Give feedback.
-
|
Ah ... I find the performance difference is very small, 15.1ms vs 15.5ms for def run_cupy_custom_kernel(height, width):
fractal = cp.empty((height, width), dtype=np.int32)
return fractal.get() |
Beta Was this translation helpful? Give feedback.
-
|
Well, to exclude the time of device-to-host copy, I tried: import cupy as cp
from cupyx.profiler import benchmark
h, w = 2048, 4096
fractal = cp.empty((h, w), dtype=cp.int32)
cupy_custom_kernel = cp.RawKernel(r'''
#include <cupy/complex.cuh>
extern "C" __global__
void cupy_custom_kernel(int height, int width, int* fractal) {
int x = blockIdx.x * blockDim.x + threadIdx.x;
int y = blockIdx.y * blockDim.y + threadIdx.y;
complex<float> j(0.0, 1.0);
complex<float> z, c;
z = c = complex<float>(-1.5 + y*1.0/(height + 1)) - j + complex<float>(x*1.5)*j/complex<float>(width + 1);
fractal[y + x * width] = 20;
for (int i = 0; i < 20; i++) {
z = z * z + c;
if (z.real() * z.real() + z.imag() * z.imag() > 4) {
fractal[y + x * width] = i;
break;
}
}
}
''', "cupy_custom_kernel", options=("--use_fast_math",))
cupy_custom_kernel.compile()
def run_cupy_custom_kernel(height, width, fractal):
griddim = (height // 32, width // 32)
blockdim = (32, 32)
cupy_custom_kernel(griddim, blockdim, (height, width, fractal))
return fractal
print(benchmark(run_cupy_custom_kernel, (h, w, fractal), n_repeat=20))
cupy_custom_kernel = cp.RawKernel(r'''
#include <cupy/complex.cuh>
extern "C" __global__
void cupy_custom_kernel(int height, int width, int* fractal) {
int y = blockIdx.x * blockDim.x + threadIdx.x;
int x = blockIdx.y * blockDim.y + threadIdx.y;
complex<float> j(0.0, 1.0);
complex<float> z, c;
z = c = complex<float>(-1.5 + y * 1.0/(height + 1)) - j + complex<float>(x * 1.5) * j / complex<float>(width + 1);
int r = 20;
for (int i = 0; i < 20; i++) {
z = z * z + c;
if (z.real() * z.real() + z.imag() * z.imag() > 4) {
r = i;
break;
}
}
fractal[x * width + y] = r;
}
''', "cupy_custom_kernel", options=("--use_fast_math",))
cupy_custom_kernel.compile()
def run_cupy_custom_kernel(height, width, fractal):
griddim = (height // 32, width // 32)[::-1]
blockdim = (32, 32)
cupy_custom_kernel(griddim, blockdim, (height, width, fractal))
return fractal
print(benchmark(run_cupy_custom_kernel, (h, w, fractal), n_repeat=20))EDIT: fix |
Beta Was this translation helpful? Give feedback.
2 replies
-
|
numba-CUDA(cudatoolkit-11.3.1 from anaconda) is a little slower than cupy(cudatoolkit-11.6.0 from conda-forge) on my device, cudatoolkit version might be responsible for this difference(669us v.s. 586us). from numba import cuda
import numpy as np
@cuda.jit(fastmath=True)
def one_pixel_numba_cuda(height, width, fractal):
x, y = cuda.grid(2) # <--- 2-dimensional CUDA grid
z = c = (
np.complex64(-1.5)
+ np.complex64(y)/np.complex64(height + 1)
- np.complex64(1j)
+ np.complex64(x)*np.complex64(1.5j)/np.complex64(width + 1)
)
fractal[x, y] = 20
for i in range(20):
z = z * z + c # <--- complex z**2 is much worse than z * z here
if z.real**2 + z.imag**2 > 4: # <--- but real-valued **2 is fine
fractal[x, y] = i
break
stream = cuda.stream()
def run_numba_cuda(height, width, fractal):
griddim = (height // 32, width // 32)
blockdim = (32, 32)
one_pixel_numba_cuda[griddim, blockdim, stream](height, width, fractal)
return fractal
h, w = 2048, 4096
fractal = cuda.device_array((h, w), dtype=np.int32, stream=stream)
run_numba_cuda(h, w, fractal)
stream.synchronize()
from time import perf_counter_ns
t = perf_counter_ns()
n = 20
for _ in range(n):
run_numba_cuda(h, w, fractal)
stream.synchronize()
print((perf_counter_ns() - t) / n / 1e3) # 669us |
Beta Was this translation helpful? Give feedback.
-
|
what is the difference of the first the the second cupy run? |
Beta Was this translation helpful? Give feedback.
Answer selected by
jpivarski
-
|
It seems that JAX is slower: import jax
def run_jax_kernel(fractal):
h, w = fractal.shape
y, x = jax.numpy.ogrid[-1:0:h*1j, -1.5:0:w*1j]
z = c = x + y * 1j
for i in range(20):
z = z * z + c
diverged = z.real * z.real + z.imag * z.imag > 4 # EDIT: fixed from z.read * z.imag > 4
diverging_now = diverged & (fractal == 20)
fractal = jax.numpy.where(diverging_now, i, fractal)
return fractal
run_jax_gpu_kernel = jax.jit(run_jax_kernel)
def run_jax_gpu(fractal):
run_jax_gpu_kernel(fractal).block_until_ready()
fractal = jax.numpy.full((2048, 4096), 20, dtype=jax.numpy.int32)
run_jax_gpu(fractal)
from time import perf_counter_ns
t = perf_counter_ns()
for _ in range(20):
run_jax_gpu(fractal)
print((perf_counter_ns() - t) / 20 / 1e3) # ~410us # EDIT |
Beta Was this translation helpful? Give feedback.
6 replies
-
|
It seems that JAX device-to-host is much slower on my device. f = [jax.numpy.full((2048, 4096), 20, dtype=np.int32).block_until_ready() for _ in range(20)]
from time import perf_counter_ns
t = perf_counter_ns()
for i in range(20):
np.asarray(f[i])
print((perf_counter_ns() - t) / 20 / 1e6) # 13.5~14.5ms |
Beta Was this translation helpful? Give feedback.
-
|
At first, I developed this on Google Colab, then moved to my computer and got more reproducible timing. It probably still works on Google Colab, if You've given me a lot of things to try (and I can only try them when I get home tonight). Yesterday, I couldn't think of anything else to try. All of them would be "fixes" to the non-JAX code, so if any one of them is responsible, then that only goes to show the value of writing array-oriented code and letting JAX optimize it. (If possible, within JAX's restrictions.) Hopefully, one of the five checkboxes above does it, and then I'll have this new story to tell. If not... then I'm still leaning toward the conclusion that I made some mistake in the non-JAX code, rather than some mistake in benchmarking the JAX code. Yesterday, I thought it might be that the JAX benchmark was incorrectly optimistic, but you've found a lot more open questions in the non-JAX code. I had been leaning toward thinking that the benchmark was wrong because the non-JAX ones were so close to each other, but the kinds of mistakes and potential mistakes you've pointed out are ones that would apply equally to all of the non-JAX ones, which would explain why they're so close to each other.
For me, not copying the array back to host was "one half" ms (compare to your 0.375 ms) and copying it back was 3 ms, so the copy dominated, but the non-JAX GPU code was at 22 and 24 ms. (All numbers I remember off the top of my head, now.) I must have a fast interconnect. It's a System76 machine. |
Beta Was this translation helpful? Give feedback.
-
|
My hand written kernel without copying was 0.246ms. I think you could try my snippet above. |
Beta Was this translation helpful? Give feedback.
-
|
|
Beta Was this translation helpful? Give feedback.
-
|
I will be starting with your hand-written kernel. Thanks! |
Beta Was this translation helpful? Give feedback.
-
|
It's resolved; thanks for all your help, @YouJiacheng! The main thing that I was missing in my CPU implementations was that I was using I'm still missing something in the CPU implementation, because all of mine (pybind11, Cython, Numba, Numba) are consistently 40% worse than The main thing that I was missing in my GPU implementations was the use of The final plot for my computer (specs as given above) is
You can see that the GPU implementations are all about the same as one another, the JAX CPU implementation is about 40% better than the other four, NumPy and CuPy without controlling for intermediate arrays is much worse than careful compilation, but much better than nothing. Python is on the far right, representing "nothing." The notebook runs as-is on Google Colab because that environment happens to have only one CPU (at my usage tier, anyway). Here's what the plot looks like when run there:
Pretty similar, though pybind11 and Cython are worse. Maybe the C++ compiler is different or maybe external calls to binaries are different for some reason? Anyway, I didn't enter into this project expecting to be as impressed with I've also updated the gist. |
Beta Was this translation helpful? Give feedback.
5 replies
-
|
Swapping column-major/row-major in my benchmark snippet (without copying) make 270us => 390us. |
Beta Was this translation helpful? Give feedback.
-
|
BTW, python for-loop element-wise update might be faster if native python list is used(numpy array has dispatch cost), but using numpy can be faster for constructing the initial value of |
Beta Was this translation helpful? Give feedback.
-
That's actually what I meant: it's only a 30% difference (but I took the faster one). I agree about the Python version, it would be faster to use builtin types, though I have to decide how the problem is posed. As it is, every implementation has to produce the same end-state: a NumPy array in RAM. Maybe it would be faster to do the calculation with built-in types and convert the final list into a NumPy array. Anyway, whatever is done there, it will still be a bar that goes far to the right. |
Beta Was this translation helpful? Give feedback.
-
|
Oh - |
Beta Was this translation helpful? Give feedback.
-
|
I believe there is memory-access and computation overlapping: int r = 20;
for (int i = 0; i < 20; i++) {
z = z * z + c;
if (z.real() * z.real() + z.imag() * z.imag() > 4) {
r = i;
break;
}
}
fractal[x * width + y] = r;is significantly faster than fractal[x * width + y] = 20;
for (int i = 0; i < 20; i++) {
z = z * z + c;
if (z.real() * z.real() + z.imag() * z.imag() > 4) {
fractal[x * width + y] = i;
break;
}
}when I use colum-major(i.e. |
Beta Was this translation helpful? Give feedback.
-
|
Chiming in here (this is a fascinating thread) to comment that JAX/XLA uses some but not all fastmath optimisations by default. If you're using all of fastmath for the other approaches then for fairness' sake JAX/XLA should be allowed to as well. No idea if that'll actually effect your end result, of course. I mean JAX is winning anyway, but obviously I'm curious to know if the margin can be improved. |
Beta Was this translation helpful? Give feedback.
3 replies
-
|
Good point: I should look into turning on full fastmath in JAX. It was the second most important correction to the CPU implementations and it's what pushed Numba-CUDA past JAX on the GPU, though the reason I'm using a log plot is to de-emphasize differences smaller than a factor of two. Because of that success, I assumed that JAX was using fastmath. Julia was also in the back of my mind during all of this. In principle, though, it should be just the same as Numba. In terms of abstraction, Julia exposes you to as many details as Numba. (In general, I tried to get a basis set of all different levels of abstraction, one representative each. So, for instance, PyCUDA would be redundant with CuPy with raw kernels.) |
Beta Was this translation helpful? Give feedback.
-
Julia is usually considered to be more human-friendly and expressive than numba, and its "native"(with language level jit) performance is satisfactory. |
Beta Was this translation helpful? Give feedback.
-
|
|
Beta Was this translation helpful? Give feedback.
-
Julia benchmark vs. Jax vs. Numbatldr:
follwoing discussion on Julia discourse (thanks to @chriselrod), and after realizing Jax unrolls the # NOT using fastmath
function run_julia(height, width)
y = range(-1.0f0, 0.0f0; length = height) # need Float32 because Jax defaults to it
x = range(-1.5f0, 0.0f0; length = width)
c = x' .+ y*im
fractal = fill(Int32(20), height, width)
# this checks if indicies are compatible between `c` and `fractal`
@inbounds for idx in eachindex(c, fractal)
_c = c[idx]
z = _c
m = true
Base.Cartesian.@nexprs 20 i -> begin
z = z^2 + _c
az4 = abs2(z) > 4f0
fractal[idx] = ifelse(m&az4, Int32(i), fractal[idx]) # 32-bit Int, same reason as above
m &= (!az4)
end
end
return fractal
endJaxIn [8]: %%timeit -o
...: run_jax_cpu(2000, 3000)
97.9 ms ± 870 µs per loop (mean ± std. dev. of 7 runs, 1 loop each)
Out[8]: <TimeitResult : 97.9 ms ± 870 µs per loop (mean ± std. dev. of 7 runs, 1 loop each)>Julia (with unroll & without fastmath)julia> @benchmark run_julia(2000,3000)
BenchmarkTools.Trial: 93 samples with 1 evaluation.
Range (min … max): 48.687 ms … 114.762 ms ┊ GC (min … max): 0.31% … 54.80%
Time (median): 52.597 ms ┊ GC (median): 0.89%
Time (mean ± σ): 53.969 ms ± 8.555 ms ┊ GC (mean ± σ): 3.34% ± 7.73%
▇█
▄▁▁██▄▄▁▁▁▁▁▁▄▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▄ ▁
48.7 ms Histogram: log(frequency) by time 107 ms <
Memory estimate: 68.66 MiB, allocs estimate: 4.Additional comparison with NumbaNumbaIn [6]: %%timeit -o
...: run_numba(2000, 3000)
143 ms ± 1.16 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
Out[6]: <TimeitResult : 143 ms ± 1.16 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)>Julia (without unroll & with fastmath)@inline function fast2(x) # pending PR to add this as the fastmath routine for complex^2
r = real(x)
i = imag(x)
Complex(fma(r, r, -i * i), fma(r, i, i * r))
end
function run_julia(height, width)
y = range(-1.0f0, 0.0f0; length = height)
x = range(-1.5f0, 0.0f0; length = width)
c = x' .+ y*im
fractal = fill(Int32(20), height, width)
@inbounds @fastmath for idx in eachindex(c)
_c = c[idx]
z = _c
for i = 1:20
z = fast2(z) + _c
if abs2(z) > 4f0
fractal[idx] = i
break
end
end
end
return fractal
end
julia> @benchmark run_julia(2000,3000)
BenchmarkTools.Trial: 46 samples with 1 evaluation.
Range (min … max): 105.716 ms … 112.512 ms ┊ GC (min … max): 0.00% … 0.72%
Time (median): 110.110 ms ┊ GC (median): 0.00%
Time (mean ± σ): 109.905 ms ± 1.457 ms ┊ GC (mean ± σ): 0.38% ± 0.52%
▁ ▄ ▁▁▁▁▄ ▁ ▄ █
▆▁▁▁▁▁▁▁▁▁▆▁▁▆▆▆▁▁▁█▁▁▁▁▁▁▁▁▆▆▆█▁▆▆▆█████▆█▆█▁▆▁█▁▆▆▁▆▆▆▆▁▁▁▆ ▁
106 ms Histogram: frequency by time 113 ms <
Memory estimate: 68.66 MiB, allocs estimate: 4.Platform information and Image output for debugging / sanity checkjulia> versioninfo(verbose=true)
Julia Version 1.8.0-beta3
Commit 3e092a2521 (2022-03-29 15:42 UTC)
Platform Info:
OS: Linux (x86_64-pc-linux-gnu)
uname: Linux 5.18.6-arch1-1 #1 SMP PREEMPT_DYNAMIC Wed, 22 Jun 2022 18:10:56 +0000 x86_64 unknown
CPU: 11th Gen Intel(R) Core(TM) i5-1135G7 @ 2.40GHz:
speed user nice sys idle irq
#1 4200 MHz 47711 s 0 s 15165 s 1050914 s 18726 s
#2 400 MHz 57317 s 0 s 15044 s 25843 s 1600 s
#3 2800 MHz 58279 s 0 s 14516 s 26112 s 1707 s
#4 1300 MHz 58318 s 0 s 14387 s 25701 s 1746 s
#5 4200 MHz 54057 s 0 s 13005 s 26334 s 1868 s
#6 1962 MHz 57398 s 1 s 15431 s 26493 s 1450 s
#7 400 MHz 58745 s 0 s 14183 s 26216 s 1598 s
#8 400 MHz 58657 s 1 s 14181 s 25788 s 1460 s
Memory: 31.14313507080078 GB (17520.08984375 MB free)
Uptime: 279087.59 sec
Load Avg: 1.4 1.22 0.99
WORD_SIZE: 64
LIBM: libopenlibm
LLVM: libLLVM-13.0.1 (ORCJIT, tigerlake)
Threads: 1 on 8 virtual cores
julia> using Plots
julia> heatmap(run_julia(2000, 3000))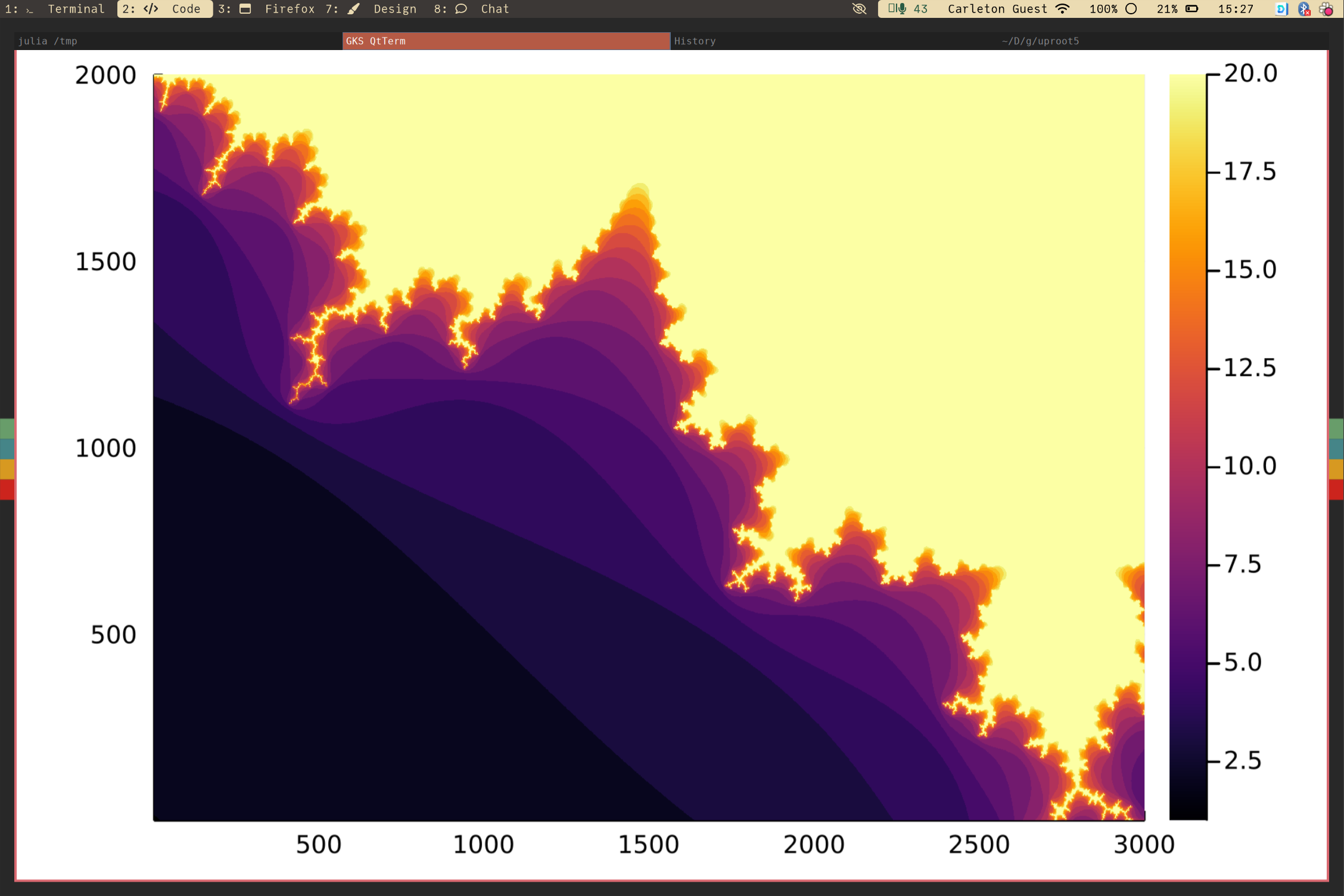
|
Beta Was this translation helpful? Give feedback.
3 replies
-
|
In terms of "what the compiler should do", note that I shared a version that was around four times faster than this one, while also not fully unrolling the loop meaning it wasn't "cheating"/specializing, unlike these versions, and would do much better with given more iterations due to early stopping/breaking out of the loop. |
Beta Was this translation helpful? Give feedback.
-
|
Chris is referring to this: https://discourse.julialang.org/t/hard-to-beat-numba-jax-loop-for-generating-mandelbrot/82725/49 |
Beta Was this translation helpful? Give feedback.
-
|
8x faster(Chris' version) than JAX, amazing! Wow! |
Beta Was this translation helpful? Give feedback.
-
|
Any chance we can get a Dex benchmark @axch or @apaszke ? Maybe with the new vectorization pass? (or relying on LLVM). The levenshtein distance example is really cool |
Beta Was this translation helpful? Give feedback.
0 replies
-
Julia GPU (CPU) Kernel programming
You can write a vendor-agnostic kernel of this algorithm with KernelAbstractions.jl and it would run on NVIDIA, AMD, Intel GPUs alike (pending oneAPI PR), I will demonstrate the point with a kernel instantiated on CUDA device: using KernelAbstractions, CUDAKernels, CUDA
@kernel function julia_kernel!(c, fractal)
I = @index(Global)
_c = c[I]
z = _c
@inbounds for i = 1:20
z = z^2 + _c
if abs2(z) > 4f0
fractal[I] = Int32(i)
break
end
end
end
function run_julia_gpu(height, width)
y = CuArray(range(-1.0f0, 0.0f0; length = height))
x = CuArray(range(-1.5f0, 0.0f0; length = width))
c = x' .+ y*im
fractal = CUDA.fill(Int32(20), height, width)
# the 32^2 is comparible to gridsize in Numba-CUDA
kernel! = julia_kernel!(CUDADevice(), 32^2) # we instantiate a kernel with vendor info
kernel!(c, fractal; ndrange=size(c))
return Array(fractal) # copy back to CPU, blocking
end
julia> @benchmark run_julia_gpu(2000,3000)
BenchmarkTools.Trial: 1279 samples with 1 evaluation.
Range (min … max): 2.349 ms … 12.656 ms ┊ GC (min … max): 0.00% … 11.64%
Time (median): 2.419 ms ┊ GC (median): 0.00%
Time (mean ± σ): 3.908 ms ± 3.135 ms ┊ GC (mean ± σ): 7.66% ± 14.73%
█ ▂ ▁▂ ▂
█▄▁▁▁▁▁▁▁▁▁▁▃▁▁▁▁▄█▇▆▅▃▃▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁██▆▁▁▅██ ▇
2.35 ms Histogram: log(frequency) by time 11.9 ms <
Memory estimate: 22.91 MiB, allocs estimate: 130.Use CPU as (bad) kernal executorCPU is a very bad GPU (for this kind of work), but just to show that the kernel function is indeed vendor-agnostic, without changing the kernel function definition: function run_julia_cpu_jaxstype(height, width)
y = range(-1.0f0, 0.0f0; length = height)
x = range(-1.5f0, 0.0f0; length = width)
c = x' .+ y*im
fractal = fill(Int32(20), height, width)
kernel! = julia_kernel!(CPU(), length(c)÷Threads.nthreads()) # we're using 1-thread here
event = kernel!(c, fractal; ndrange=length(c))
wait(event) # not copying back, need to block here
return fractal
end
julia> @benchmark run_julia_gpu(2000,3000)
BenchmarkTools.Trial: 28 samples with 1 evaluation.
Range (min … max): 176.828 ms … 185.904 ms ┊ GC (min … max): 0.00% … 0.72%
Time (median): 178.417 ms ┊ GC (median): 0.49%
Time (mean ± σ): 178.964 ms ± 2.117 ms ┊ GC (mean ± σ): 0.41% ± 0.39%
▃ ▃▃ █ █ █ ▃ ▃
█▁▇▁▇▇██▇█▇█▇▁▇▁█▁▁█▁▁█▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▇▇ ▁
177 ms Histogram: frequency by time 186 ms <
Memory estimate: 68.67 MiB, allocs estimate: 21.CUDA Device Info |
Beta Was this translation helpful? Give feedback.
3 replies
-
|
As the author of KernelAbstractions I hasten to add that I never invested much time in improving it's CPU performance, there are many low hanging fruits, but my focus has been GPU first. @Moelf you are not using a single thread for your example, but your grain-size is one. Performance would likely be better with a much larger grain size. |
Beta Was this translation helpful? Give feedback.
-
|
you're right, actually, I was accidentally cheating by running this in 2 threads. Julia-CPU-Kernal is 2x slower than Jax-CPU-kernal, grain size doesn't change, if too big actually hurts performance |
Beta Was this translation helpful? Give feedback.
-
|
I also created an unrolled kernel with KernelAbstraction, since it usually showed better results: @kernel function julia_kernel_unroll!(c, fractal)
I = @index(Global)
_c = c[I]
z = _c
m = true
@inbounds Base.Cartesian.@nexprs 20 i -> begin
z = z^2 + _c
az4 = abs2(z) > 4f0
fractal[I] = ifelse(m&az4, Int32(i), fractal[I]) # 32-bit Int, same reason as above
m &= (!az4)
end
endStill the same performance on GPU. |
Beta Was this translation helpful? Give feedback.
-
|
I actually have the opposite issue - why is jax so slow compared to cupy ? For matrix multiplication, cupy is 5x faster on my machine while times are comparable for SVD |
Beta Was this translation helpful? Give feedback.
8 replies
-
|
77025.772 us- It seems there is something wrong with |
Beta Was this translation helpful? Give feedback.
-
|
It's all run as one block in a notebook. I tried multiple runs, putting cupy calculation first, etc. Very weird and huge difference with times given by my initial snippet |
Beta Was this translation helpful? Give feedback.
-
|
Can you check if the result makes sense? |
Beta Was this translation helpful? Give feedback.
-
|
Yes, using my original snippet : |
Beta Was this translation helpful? Give feedback.
-
|
An old thread, but noting for the record that the reason for @j-bac 's slow
|
Beta Was this translation helpful? Give feedback.
-
|
More information from @mjbaldwin: there's a compilation time/runtime trade-off in the number of Mandelbrot iterations, which is fixed at 20 in this example, but might be much larger in a similar problem. |
Beta Was this translation helpful? Give feedback.
1 reply
-
|
that makes sense, since Jax's approach is fully unroll the entire inner loop. so in fact different number of loops causes completely different function body being compiled |
Beta Was this translation helpful? Give feedback.
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment
Well, to exclude the time of device-to-host copy, I tried: