Implementing Kaczmarz in Jax #11547
-
|
Kaczmarz is popular outside of DL (aka normalized LMS in Signal Processing, ART in tomography), what would be a good way of implementing it in Jax? Basic idea:
A batched version with multiclass predictor g, would look as follows: |
Beta Was this translation helpful? Give feedback.
Replies: 4 comments 9 replies
-
|
Assume num of elements y = g(x, w)
dg_vec = jax.jacrev(lambda w: g(x, w)(w)
df_vec_T = jax.jacfwd(lambda y: f(y, w))(y)
# dg_vec[c] = dg
# df_vec_T[..., c] = df, assume w is an array |
Beta Was this translation helpful? Give feedback.
-
|
Thanks so much for this question! I pulled @froystig in to think about this, and to teach me what Kaczmarz is. We wrote this comment together! Let's change notation and clarify the problem statement: let's say we have To draw an analogy to the linear least squares setting, we can make a multiclass generalization of Eq. 5.2 of this paper. In that setting, Back in the nonlinear and non-least-squares setting, substituting back import jax
import jax.numpy as jnp
def kaczmarz_step(f, g, w, x):
y, g_vjp = jax.vjp(lambda w: g(w, x), w)
A, = jax.vmap(g_vjp)(jnp.eye(y.shape[0])) # assumes w.ndim >> y.ndim
return (jax.grad(f)(y) / (A * A).sum(1)) @ AIf we want to reduce memory usage and not instantiate import jax
import jax.numpy as jnp
def kaczmarz_step(f, g, w, x):
y, g_vjp = jax.vjp(lambda w: g(w, x), w)
normsq = jax.lax.map(lambda e: (g_vjp(e)[0]**2).sum(), jnp.eye(y.shape[0]))
return g_vjp(jax.grad(f)(y) / normsq)[0]What do you think? Is this generalization of Kaczmarz (to nonlinear and multiclass) the one you're looking for? It would be great to validate this numerically against some known reference implementation and/or problem. |
Beta Was this translation helpful? Give feedback.
-
|
Thanks for the in-depth response!
batch-Kaczmarz with least-squares loss converges in 1 step for any orthogonal set of examples (whereas GD needs them to be orthonormal) I've tested your implementation, and it passes this test -- colab |
Beta Was this translation helpful? Give feedback.
-
|
Turns out there's a much better formulation for Kaczmarz for multiclass problems. The For f(g(x)) where f is the loss function and g(x) is the model, we have the following update Computing this update has almost the same FLOPs as regular gradient step, but I suspect wall-clock time is 2x worse, since the sum over weighted per-example gradients |
Beta Was this translation helpful? Give feedback.
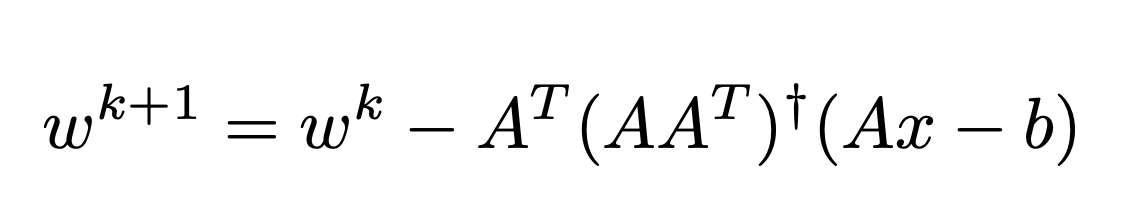
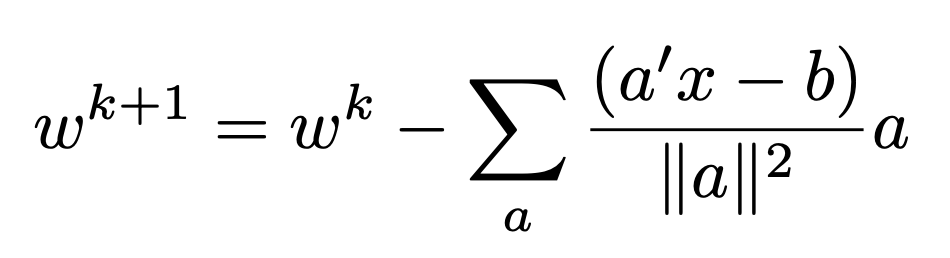



Thanks so much for this question! I pulled @froystig in to think about this, and to teach me what Kaczmarz is. We wrote this comment together!
Let's change notation and clarify the problem statement: let's say we have
h = f . gwhereg: R^d -> R^nis the prediction function, withdthe dimension of the parameter andnthe number of classes (suppressing the dependence on input dataxfor convenience), andf : R^n -> Ris the loss function. (Noticefshouldn't have an input of dimensiond, i.e. the weights, a typo in the OP we think!) Sayw ∈ R^dis the current parameter. Notice that∇f(g(w)) ∈ R^n, and∂g(w) ∈ R^{n x d}, where the latter is just notation for the Jacobian matrix.To draw an…