Why is my divide and conquer recursive function so slow to compile?

[AdrienCorenflos]

Hello,

I have a problem which I can easily phrase in terms of a divide and conquer approach (with parallelism across adjacent elements), a bit similar to prefix sum algorithms (associative_scan, see https://github.com/google/jax/blob/62603fde67eea6087e3b094f72f7cc214cf9701c/jax/_src/lax/control_flow.py#L2390).

I have successfully implemented it, but the compilation time increases dramatically as the size of the input changes. I would like to understand why this is the case, and why in comparison associative_scan is much faster to compile. I have reduced the problem to a cumulative sum example in order to be able to compare implementations more easily. The algo then takes a very simple form:

from functools import partial

from jax import jit
import jax.numpy as jnp


@partial(jit, static_argnums=(1,))
def recursive_cumsum(array, combine):
    T = array.shape[0]
    if T == 1:
        return array
    else:
        l, r = jnp.array_split(array, 2)
        return combine(recursive_cumsum(l, combine), recursive_cumsum(r, combine))

where def combine(l, r) is either combine_1 or combine_2 which encode backward and forward cumulative sum, respectively, by adding the first value of the right array to all the elements of the left one for combine_1 and vice versa for combine_2 (note that the style of the combination functions is my main constraint: they need to act upon all tensors).

@jit
def combine_1(l, r):
    '''Reverse cumsum'''
    l = l + r[0]
    return jnp.concatenate([l, r])

@jit
def combine_2(l, r):
    '''cumsum'''
    r = r + l[-1]
    return jnp.concatenate([l, r])

This creates a massive compilation overhead as can be seen in the following snippet

from jax import lax
import numpy as np

N = 153
arr = jnp.array(np.random.randn(N))

assoc_scan_version = jit(lambda array: lax.associative_scan(lambda a, b: a + b, array))  # force jitting

recursive_sum(arr, combine_2).block_until_ready()  # takes 1.5s to compile, and gets worse as N grows
assoc_scan_version(arr).block_until_ready()  # takes 150ms and doesn't get that bad as N grows

I thought this could be related to some tail recursion effects, and I have therefore also implemented a non-recursive version where I handle the stack myself. While this improves a bit the compilation time, it is still scaling very poorly with N, and doesn't approach associative_scan compilation speed whatsoever. It can be found below for reference.

import math

def pairwise(iterable):
    a = iter(iterable)
    return zip(a, a)

@partial(jit, static_argnums=(1,))
def split_arr_cumsum(array, combine):
    T = array.shape[0]
    n_splits = T 
    splitted_arrays = jnp.array_split(array, n_splits)
    for k in range(0, int(math.ceil(math.log2(T + 1)) - 1)):
        res = []
        if len(splitted_arrays) % 2 != 0:
            splitted_arrays = [combine(splitted_arrays[0], 
                                       splitted_arrays[1]), 
                               *splitted_arrays[2:]]
        # Essentially I would like the below to be a vmap type of call.
        for left, right in pairwise(splitted_arrays): # in parallel
            res.append(combine(left, right))
        splitted_arrays = res
    return splitted_arrays[0]

Does anyone have any idea so as to why these compile so slowly compared to associative_scan and how I can speed this up? I need to run a few experiments for increasing input sizes, and as a consequence need to recompile the function a number of times. Speeding it up would help a lot.

Thanks,

Adrien

[mattjj]

My first guess, without having yet read and grokked the code at all, is that the difference is in using jnp.array_split. The way associative_scan is written, the number of intermediate arrays and operations on those arrays scales like the depth of the tree, since each level of the tree is represented as a single array. So the size of the XLA program scales like log n for an input sequence of length n.

But using jnp.array_split we're storing each node (rather than level) in the tree as a separate array and performing separate operations on it. That way the size of the XLA program scales like n for an input of length n. Because the XLA program is exponentially larger, I'd expect the compile times could be much longer, scaling with n.

If this hypothesis is correct, then one way to attack the compile times would be to try to avoid using jnp.array_split and instead handle the data more like associative_scan. Could that be possible?

[AdrienCorenflos]

I also tried to handle the splitting via shape management (essentially pushing intermediary results into an auxiliary dimension of the array, but this only works for input sizes that are a power of two). It looks like the below, but still has some weird splitting happening, and the concatenation fails for inputs that are irregular (obviously).

Idea was: if your array is of shape (N,), expand to (N, 1), then store all pairwise cumulative sums done in parallel into an array of shape (N/2, 2), etc until you get to (1, N) and then you have your result.

@partial(jit, static_argnums=(1,))
def split_arr_sum_not_working(array, combine):
    T = array.shape[0]
    n_splits = T 
    splitted_arrays = array.reshape(-1, 1)
    for k in range(0, int(math.ceil(math.log2(T + 1)) - 1)):
        splitted_arrays = jnp.array_split(splitted_arrays, splitted_arrays.shape[0])
        if len(splitted_arrays) % 2 != 0:
            first_elem, second_elem = splitted_arrays[:2]
            combined_elem = combine(first_elem, 
                                    second_elem)
            combined_first_elem = combined_elem[:first_elem.shape[0]]
            combined_second_elem = combined_elem[first_elem.shape[0]:]
            splitted_arrays = [combined_first_elem, 
                               *splitted_arrays[2:]]
        else:
            combined_first_elem = None

        lefts, rights = zip(*pairwise(splitted_arrays))

        lefts = jnp.concatenate(lefts)
        rights = jnp.concatenate(rights)

        if len(lefts) == len(rights) == 1:
            splitted_arrays = combine(lefts[0], rights[0])
        else:
            splitted_arrays = vmap(combine)(lefts, rights)

        if combined_first_elem is not None:
            splitted_arrays = jnp.concatenate([combined_first_elem, splitted_arrays])
    return splitted_arrays

[AdrienCorenflos]

I'm checking the looks of the generated XLA program now.
EDIT: It's very much too big to be posted anywhere, ouch.

[AdrienCorenflos]

Note I just fixed a small bug in the code

[AdrienCorenflos]

This type of approach seems to almoooooost work, it doesn't give the right result, but at least I am controlling the size of the XLA program generated! This is done by using reshaping as a way to circumvent array_split, as the former is virtually free and doesn't generate a bunch of arrays everytime (by the way @mattjj you sure the recursive approach makes it exponential and not simply quadratic?).

Bit puzzled so as to where my logical mistake is though, but getting there. Will post the complete solution here when I find out, but if someone has an idea, feel free to help!

@partial(jit, static_argnums=(1,))
def split_arr_better(array, combine):
    T = array.shape[0]
    n_splits = T 
    splitted_arrays = jnp.array_split(array, n_splits)
    for k in range(0, int(math.ceil(math.log2(T + 1)) - 1)):
        K = 2 ** (k+1)
        remainder = T % K
        if remainder:
            not_divisible_bit = array[:remainder]
        else:
            not_divisible_bit = None
        rest = array[remainder:]
        reshaped_rest = rest.reshape(-1, 2 ** k)
        left = reshaped_rest[::2]
        right = reshaped_rest[1::2]

        rest_combined = vmap(combine)(left, right)
        rest_combined = rest_combined.reshape(rest.shape)
        if not_divisible_bit is not None:
            array = combine(not_divisible_bit, rest_combined)
        else:
            array = rest_combined
    return array

[AdrienCorenflos]

OK so the above works for powers of two, so if you don't feel too bad about it you can simply expand your data in a non impacting way. Here goes nothing.

def _next_power_of_2(n):
    log2n = math.log2(n)
    ceil = math.ceil(log2n)
    is_power_of_two = ceil == math.floor(log2n)
    if is_power_of_two:
        return n
    else:
        return int(2 ** ceil)

@partial(jit, static_argnums=(1,))        
def compile_efficient(array, combine):
    T = array.shape[0]
    next_power_of_2 = _next_power_of_2(T)
    array = jnp.pad(array, 
                    (0, next_power_of_2 - T), 
                    constant_values=jnp.nan)
    use_values_flag = jnp.pad(jnp.ones((T,), dtype=jnp.bool_),
                              (0, next_power_of_2 - T),
                              constant_values=False)
    
    def _pass_through(l, r):
        return jnp.concatenate([l, r])

    @vmap
    def _combine(l, use_l, r, use_r):
        use = use_l[-1] & use_r[0]
        return lax.cond(use,
                        lambda op: combine(*op),
                        lambda op: _pass_through(*op),
                        operand=(l, r))

    K = int(math.log2(next_power_of_2 + 0.1))  # 0.1 to be on the safe side.
    for k in range(0, K):
        intermediary_shape = 2 ** k
        reshaped_array = array.reshape(-1, intermediary_shape)
        reshaped_flags = use_values_flag.reshape(-1, intermediary_shape)

        combined_array = _combine(reshaped_array[::2], reshaped_flags[::2],
                                  reshaped_array[1::2], reshaped_flags[1::2])

        array = combined_array.reshape(array.shape)

    return array[:T]

[AdrienCorenflos]

@mattjj could you please confirm the above won't have unintended side effects?

[AdrienCorenflos]

So, I have tried to improve on the above, and implemented a generic reshape divide and conquer. However, the compilation speed went from fast to super slow, and all I can see as a problem would be the fact that I am now using pytrees in order to unpack arguments. The code is generic for any kind of operator but for some reason it is now

1. slow to compile
2. slower when it has been jitted!

@mattjj as you had a preliminary look at the previous iteration, would you happen to know what is happening below?

(The intermediary_results bit can be skipped at first read, the standard bit is still slow.)

import math

import jax.numpy as jnp
import jax.ops
from jax import vmap, lax
from jax.tree_util import tree_flatten, tree_unflatten

_EPS = 0.1  # this is a small float to make sure that log2(2**k) = k exactly


def _next_power_of_2(n):
    q, mod = n, 0
    k = 0
    while q > 1:
        q, mod_ = divmod(q, 2)
        mod += mod_
        k += 1
    if mod:
        k += 1
    return 2 ** k


def _pass_through(flat_tree_a, flat_tree_b):
    flat_tree = [jnp.concatenate([elem_a, elem_b], 0) for elem_a, elem_b in zip(flat_tree_a, flat_tree_b)]
    return flat_tree


def compile_efficient_combination(elems, operator, return_intermediary=False):
    flat_tree, tree_def = tree_flatten(elems)
    T = int(flat_tree[0].shape[0])
    if not all(int(elem.shape[0]) == T for elem in flat_tree[1:]):
        raise ValueError('Array inputs to associative_scan must have the same '
                         'first dimension. (saw: {})'
                         .format([elem.shape for elem in flat_tree]))

    next_power_of_2 = _next_power_of_2(T)

    def pad(flat_elem):
        dtype = flat_elem.dtype
        if jnp.issubdtype(dtype, jnp.integer):
            constant_val = 0
        else:
            constant_val = jnp.nan
        pad_width = [(0, next_power_of_2 - T)] + [(0, 0)] * (flat_elem.ndim - 1)
        return jnp.pad(flat_elem, pad_width=pad_width, constant_values=constant_val)

    padded_flat_elems = [pad(flat_elem) for flat_elem in flat_tree]
    use_values_flag = jnp.pad(jnp.ones((T,), dtype=jnp.bool_), (0, next_power_of_2 - T), constant_values=False)

    def reshape(elem, intermediary_shape):
        shape = -1, intermediary_shape, *elem.shape[1:]
        return jnp.reshape(elem, shape)

    def wrapped_operator(flat_tree_a, flat_tree_b):
        elem_a = tree_unflatten(tree_def, flat_tree_a)
        elem_b = tree_unflatten(tree_def, flat_tree_b)
        res = operator(elem_a, elem_b)
        flat_res, operator_tree_def = tree_flatten(res)
        assert tree_def == operator_tree_def, f"The operator '{operator}' should preserve the input structure, " \
                                              f"expected '{tree_def}' but got '{operator_tree_def}'"
        return flat_res

    @vmap
    def combine(flat_elem_a, use_a, flat_elem_b, use_b):
        use = use_a[-1] & use_b[0]
        return lax.cond(use,
                        lambda _: wrapped_operator(flat_elem_a, flat_elem_b),
                        lambda _: _pass_through(flat_elem_a, flat_elem_b),
                        operand=None)

    K = int(math.log2(next_power_of_2 + _EPS))

    if return_intermediary:
        intermediary_flat_elems = []
        for flat_elem in padded_flat_elems:
            flat_elem_shape = flat_elem.shape
            intermediary_elem = jnp.empty((K + 1, *flat_elem_shape), dtype=flat_elem.dtype)
            intermediary_elem = jax.ops.index_update(intermediary_elem, 0, flat_elem, indices_are_sorted=True,
                                                     unique_indices=True)
            intermediary_flat_elems.append(intermediary_elem)

    shapes = [elem.shape for elem in padded_flat_elems]
    for k in range(K):
        reshaped_flat_tree = [reshape(flat_elem, 2 ** k) for flat_elem in padded_flat_elems]
        even_elems, odd_elems = zip(*((flat_elem[::2], flat_elem[1::2]) for flat_elem in reshaped_flat_tree))
        reshaped_flags = reshape(use_values_flag, 2 ** k)
        even_flags, odd_flags = reshaped_flags[::2], reshaped_flags[1::2]
        reshaped_flat_tree = combine(even_elems, even_flags, odd_elems, odd_flags)
        padded_flat_elems = [jnp.reshape(flat_elem, shape) for flat_elem, shape in zip(reshaped_flat_tree, shapes)]

        if return_intermediary:
            intermediary_flat_elems_temp = []
            for flat_elem, intermediary_elem in zip(padded_flat_elems, intermediary_flat_elems):  # noqa
                intermediary_elem = jax.ops.index_update(intermediary_elem, k + 1, flat_elem,  # noqa
                                                         indices_are_sorted=True, unique_indices=True)  # noqa
                intermediary_flat_elems_temp.append(intermediary_elem)
            intermediary_flat_elems = intermediary_flat_elems_temp

    if return_intermediary:
        intermediary_flat_elems_temp = []
        for intermediary_elem in intermediary_flat_elems:  # noqa
            intermediary_flat_elems_temp.append(intermediary_elem[:, :T])
        return tree_unflatten(tree_def, intermediary_flat_elems_temp)
    else:
        flat_elems = []
        for elem in padded_flat_elems:  # noqa
            flat_elems.append(elem[:T])
        return tree_unflatten(tree_def, flat_elems)

It is used via:

some_structure = namedtuple("some_structure", ["x", "y"])
rng = np.random.RandomState(np_seed)

@jit
def add(a, b):
    a_x, a_y = a
    b_x, b_y = b
    b_x = b_x + a_x[-1]
    a_y = a_y + b_y[0]

    x = jnp.concatenate([a_x, b_x], 0)
    y = jnp.concatenate([a_y, b_y], 0)
    return some_structure(x, y)

jitted_compile_efficient_combination = jit(compile_efficient_combination,
                                                                  static_argnums=(1,),
                                                                  static_argnames=("return_intermediary",))
T = 2 ** 5 + 1
x_init = rng.randn(T, 3)
y_init = rng.randn(T, 4)
elems = some_structure(x_init, y_init)

result = jitted_compile_efficient_combination(elems, add)
intermediary_results = jitted_compile_efficient_combination(elems, add, return_intermediary=True)
      

Adrien

[AdrienCorenflos]

I just checked with make_jaxpr and the number of XLA generated lines is a perfect logarithm

[AdrienCorenflos]

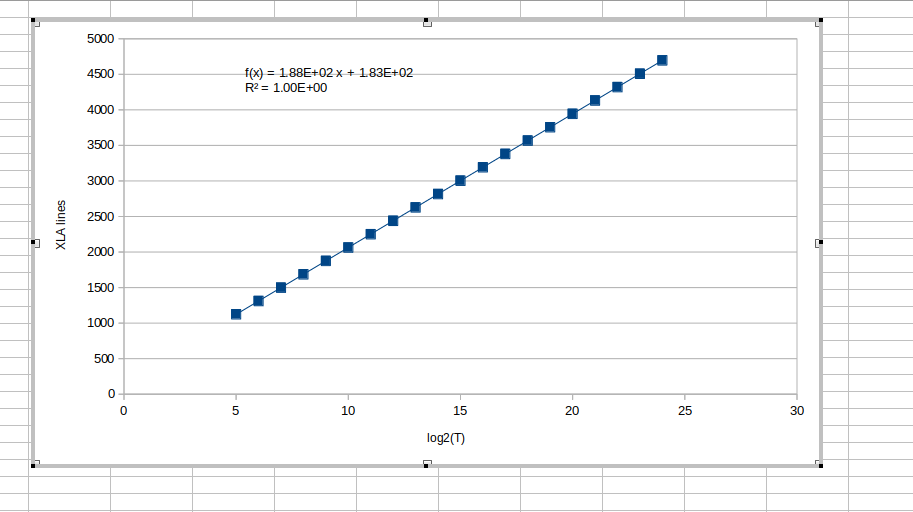
Follow up on this, I have tried to split up the parallel computations happening at the "combine" function by sending them to different devices, however it slowed the whole thing dramatically, and I am not yet sure why. I thought my arrays were gonna be properly shared and propagated but it's not the case. Do you have any idea @mattjj?

https://colab.research.google.com/drive/1frM5UgGlmky2nbpJCvPSkQIzgSt9hCis#scrollTo=Rh0lR8M1Ul4Z