-
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 1 reply
-
|
I assume this is on a GPU backend, yes? On GPU, I can't think of any way to express this functionality in terms of convolution (there doesn't really seem to be any reduction involved). But I think you can express this in terms of broadcasted indices: @functools.partial(jax.jit, static_argnums=(2,))
def overlap_merge(local_grid, global_grid, stride):
out_shape = (
(global_grid.shape[0] - 1) * stride[0] + local_grid.shape[0],
(global_grid.shape[1] - 1) * stride[1] + local_grid.shape[1],
)
out_dtype = jnp.result_type(local_grid, global_grid)
i = jnp.arange(local_grid.shape[0])
j = jnp.arange(local_grid.shape[1])
i_offset = stride[0] * jnp.arange(global_grid.shape[0])
j_offset = stride[1] * jnp.arange(global_grid.shape[1])
i_offset, j_offset, i, j = jnp.meshgrid(i_offset, j_offset, i, j, sparse=True)
return jnp.zeros(out_shape, out_dtype).at[i + i_offset, j + j_offset].add(local_grid)This returns the same results for your example inputs, and I think applies similar logic for larger inputs as well. On CPU, I find that the performance is comparable to your scan-based implementation. On GPU, it is quite a bit faster because indexed adds can take advantage of the GPU's parallelism. |
Beta Was this translation helpful? Give feedback.
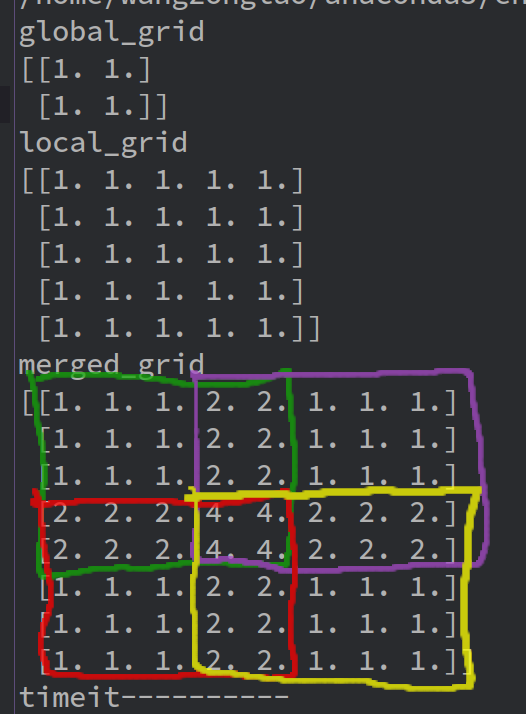
I assume this is on a GPU backend, yes? On GPU,
scanis often very inefficient because it requires serial computations, and thus can't take advantage of the parallelism inherent in GPU vectorized operations.I can't think of any way to express this functionality in terms of convolution (there doesn't really seem to be any reduction involved). But I think you can express this in terms of broadcasted indices: