|
| 1 | +# 二次贝塞尔曲线 |
| 2 | + |
| 3 | + |
| 4 | + |
| 5 | +> 声明:本文为作者学习,自定义View系列教程的笔记,自定义View是由GcsSloop原创,它的GitHub地址为:https://github.com/GcsSloop |
| 6 | +> |
| 7 | +> 教程地址为:https://github.com/GcsSloop/AndroidNote/blob/master/CustomView/Advance/%5B06%5DPath_Bezier.md |
| 8 | +
|
| 9 | +## 贝塞尔曲线简介 |
| 10 | + |
| 11 | + |
| 12 | + |
| 13 | +贝塞尔曲线(Bézier curve),又称[贝兹](http://baike.baidu.com/item/%E8%B4%9D%E5%85%B9)曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线,贝兹曲线由[线段](http://baike.baidu.com/item/%E7%BA%BF%E6%AE%B5)与[节点](http://baike.baidu.com/item/%E8%8A%82%E7%82%B9)组成,节点是可拖动的支点,线段像可伸缩的皮筋,我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线是计算机图形学中相当重要的参数曲线,在一些比较成熟的位图软件中也有贝塞尔[曲线工具](http://baike.baidu.com/item/%E6%9B%B2%E7%BA%BF%E5%B7%A5%E5%85%B7),如PhotoShop等。在Flash4中还没有完整的曲线工具,而在Flash5里面已经提供出贝塞尔曲线工具。 |
| 14 | + |
| 15 | +贝塞尔曲线于1962,由法国工程师皮埃尔·贝塞尔(Pierre Bézier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau演算法开发,以稳定数值的方法求出贝兹曲线。 |
| 16 | + |
| 17 | +以上内容从采取自百度百科 |
| 18 | + |
| 19 | +贝塞尔曲线目前被广泛应用于计算机制图中,可以说贝塞尔曲线奠定了计算机制图的基础。 |
| 20 | + |
| 21 | + |
| 22 | + |
| 23 | +# Android中绘制Path的API |
| 24 | + |
| 25 | + |
| 26 | + |
| 27 | +Android中绘制Path常用方法: |
| 28 | + |
| 29 | +以下方法转载至GcsSloop的自定义View系列教程:https://github.com/GcsSloop/AndroidNote/tree/master/CustomView/README.md |
| 30 | + |
| 31 | + |
| 32 | + |
| 33 | +| 作用 | 相关方法 | 备注 | |
| 34 | +| ----------- | ---------------------------------------- | ---------------------------------------- | |
| 35 | +| 移动起点 | moveTo | 移动下一次操作的起点位置 | |
| 36 | +| 设置终点 | setLastPoint | 重置当前path中最后一个点位置,如果在绘制之前调用,效果和moveTo相同 | |
| 37 | +| 连接直线 | lineTo | 添加上一个点到当前点之间的直线到Path | |
| 38 | +| 闭合路径 | close | 连接第一个点连接到最后一个点,形成一个闭合区域 | |
| 39 | +| 添加内容 | addRect, addRoundRect, addOval, addCircle, addPath, addArc, arcTo | 添加(矩形, 圆角矩形, 椭圆, 圆, 路径, 圆弧) 到当前Path (注意addArc和arcTo的区别) | |
| 40 | +| 是否为空 | isEmpty | 判断Path是否为空 | |
| 41 | +| 是否为矩形 | isRect | 判断path是否是一个矩形 | |
| 42 | +| 替换路径 | set | 用新的路径替换到当前路径所有内容 | |
| 43 | +| 偏移路径 | offset | 对当前路径之前的操作进行偏移(不会影响之后的操作) | |
| 44 | +| 贝塞尔曲线 | quadTo, cubicTo | 分别为二次和三次贝塞尔曲线的方法 | |
| 45 | +| rXxx方法 | rMoveTo, rLineTo, rQuadTo, rCubicTo | **不带r的方法是基于原点的坐标系(偏移量), rXxx方法是基于当前点坐标系(偏移量)** | |
| 46 | +| 填充模式 | setFillType, getFillType, isInverseFillType, toggleInverseFillType | 设置,获取,判断和切换填充模式 | |
| 47 | +| 提示方法 | incReserve | 提示Path还有多少个点等待加入**(这个方法貌似会让Path优化存储结构)** | |
| 48 | +| 布尔操作(API19) | op | 对两个Path进行布尔运算(即取交集、并集等操作) | |
| 49 | +| 计算边界 | computeBounds | 计算Path的边界 | |
| 50 | +| 重置路径 | reset, rewind | 清除Path中的内容<br/> **reset不保留内部数据结构,但会保留FillType.**<br/> **rewind会保留内部的数据结构,但不保留FillType** | |
| 51 | +| 矩阵操作 | transform | 矩阵变换 | |
| 52 | + |
| 53 | + |
| 54 | + |
| 55 | +贝塞尔曲线应用简单场景: |
| 56 | + |
| 57 | +- QQ小红点拖拽效果 |
| 58 | +- 平滑的折线图的制作 |
| 59 | +- 阅读软件的翻书效果 |
| 60 | + |
| 61 | + |
| 62 | + |
| 63 | +## 绘制贝塞尔曲线 |
| 64 | + |
| 65 | + |
| 66 | + |
| 67 | +### 一阶贝塞尔曲线 |
| 68 | + |
| 69 | + |
| 70 | + |
| 71 | +一阶贝塞尔曲线的原理就是一条直线,其实就是直接画了一个Path出来,在这里不做过多的介绍,本文主要介绍的是二阶的贝塞尔曲线。 |
| 72 | + |
| 73 | + |
| 74 | + |
| 75 | +### 二阶贝塞尔曲线 |
| 76 | + |
| 77 | + |
| 78 | + |
| 79 | +二阶贝塞尔曲线效果图: |
| 80 | + |
| 81 | + |
| 82 | + |
| 83 | + |
| 84 | + |
| 85 | + |
| 86 | + |
| 87 | +### 实现原理 |
| 88 | + |
| 89 | +二阶曲线由两个数据点(A 和 C),一个控制点(B)来描述曲线状态,大致如下: |
| 90 | + |
| 91 | + |
| 92 | + |
| 93 | +上图中红色曲线部分就是传说中的二阶贝塞尔曲线,那么这条红色曲线是如何生成的呢?接下来我们就以其中的一个状态分析一下: |
| 94 | + |
| 95 | + |
| 96 | + |
| 97 | +连接AB BC,并在AB上取点D,BC上取点E,使其满足条件: |
| 98 | +<img src="http://chart.googleapis.com/chart?cht=tx&chl=%5Cfrac%7BAD%7D%7BAB%7D%20%3D%20%5Cfrac%7BBE%7D%7BBC%7D" style="border:none;" /> |
| 99 | + |
| 100 | + |
| 101 | + |
| 102 | +连接DE,取点F,使得: |
| 103 | + |
| 104 | +``AD/AB = BE/BC = DF/DE`` |
| 105 | + |
| 106 | + |
| 107 | + |
| 108 | +这样获取到的点F就是贝塞尔曲线上的一个点,动态过程如下: |
| 109 | + |
| 110 | +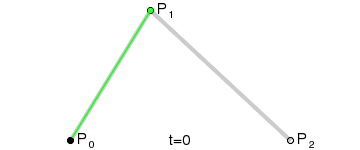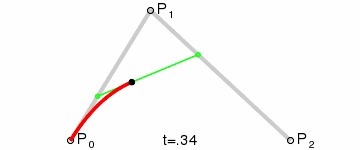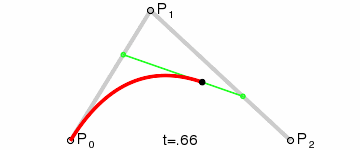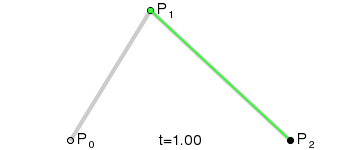 |
| 111 | + |
| 112 | + |
| 113 | + |
| 114 | +### 实现代码 |
| 115 | + |
| 116 | + |
| 117 | + |
| 118 | +```java |
| 119 | +public class Bezier2 extends View { |
| 120 | + |
| 121 | + private Paint mPaint; |
| 122 | + private int centerX, centerY; |
| 123 | + |
| 124 | + private PointF start, end, control; |
| 125 | + |
| 126 | + public Bezier2(Context context) { |
| 127 | + super(context); |
| 128 | + mPaint = new Paint(); |
| 129 | + mPaint.setColor(Color.BLACK); |
| 130 | + mPaint.setStrokeWidth(8); |
| 131 | + mPaint.setStyle(Paint.Style.STROKE); |
| 132 | + mPaint.setTextSize(60); |
| 133 | + |
| 134 | + start = new PointF(0,0); |
| 135 | + end = new PointF(0,0); |
| 136 | + control = new PointF(0,0); |
| 137 | + } |
| 138 | + |
| 139 | + |
| 140 | + public Bezier2(Context context, @Nullable AttributeSet attrs) { |
| 141 | + super(context, attrs); |
| 142 | + mPaint = new Paint(); |
| 143 | + mPaint.setColor(Color.BLACK); |
| 144 | + mPaint.setStrokeWidth(8); |
| 145 | + mPaint.setStyle(Paint.Style.STROKE); |
| 146 | + mPaint.setTextSize(60); |
| 147 | + |
| 148 | + start = new PointF(0,0); |
| 149 | + end = new PointF(0,0); |
| 150 | + control = new PointF(0,0); |
| 151 | + } |
| 152 | + |
| 153 | + @Override |
| 154 | + protected void onSizeChanged(int w, int h, int oldw, int oldh) { |
| 155 | + super.onSizeChanged(w, h, oldw, oldh); |
| 156 | + centerX = w/2; |
| 157 | + centerY = h/2; |
| 158 | + |
| 159 | + // 初始化数据点和控制点的位置 |
| 160 | + start.x = centerX-200; |
| 161 | + start.y = centerY; |
| 162 | + end.x = centerX+200; |
| 163 | + end.y = centerY; |
| 164 | + control.x = centerX; |
| 165 | + control.y = centerY-100; |
| 166 | + } |
| 167 | + |
| 168 | + @Override |
| 169 | + public boolean onTouchEvent(MotionEvent event) { |
| 170 | + // 根据触摸位置更新控制点,并提示重绘 |
| 171 | + control.x = event.getX(); |
| 172 | + control.y = event.getY(); |
| 173 | + invalidate(); |
| 174 | + return true; |
| 175 | + } |
| 176 | + |
| 177 | + @Override |
| 178 | + protected void onDraw(Canvas canvas) { |
| 179 | + super.onDraw(canvas); |
| 180 | + |
| 181 | + // 绘制数据点和控制点 |
| 182 | + mPaint.setColor(Color.GRAY); |
| 183 | + mPaint.setStrokeWidth(20); |
| 184 | + canvas.drawPoint(start.x,start.y,mPaint); |
| 185 | + canvas.drawPoint(end.x,end.y,mPaint); |
| 186 | + canvas.drawPoint(control.x,control.y,mPaint); |
| 187 | + |
| 188 | + // 绘制辅助线 |
| 189 | + mPaint.setStrokeWidth(4); |
| 190 | + canvas.drawLine(start.x,start.y,control.x,control.y,mPaint); |
| 191 | + canvas.drawLine(end.x,end.y,control.x,control.y,mPaint); |
| 192 | + |
| 193 | + // 绘制贝塞尔曲线 |
| 194 | + mPaint.setColor(Color.RED); |
| 195 | + mPaint.setStrokeWidth(8); |
| 196 | + |
| 197 | + Path path = new Path(); |
| 198 | + |
| 199 | + path.moveTo(start.x,start.y); |
| 200 | + path.quadTo(control.x,control.y,end.x,end.y); |
| 201 | + |
| 202 | + canvas.drawPath(path, mPaint); |
| 203 | + } |
| 204 | +} |
| 205 | + |
| 206 | +``` |
| 207 | + |
| 208 | + |
| 209 | + |
| 210 | +代码地址:https://github.com/linsir6/mCustomView/tree/master/Bezier |
| 211 | + |
| 212 | + |
| 213 | + |
| 214 | + |
| 215 | + |
| 216 | + |
| 217 | + |
| 218 | + |
| 219 | + |
| 220 | + |
| 221 | + |
| 222 | + |
| 223 | + |
| 224 | + |
| 225 | + |
| 226 | + |
| 227 | + |
| 228 | + |
| 229 | + |
| 230 | + |
| 231 | + |
| 232 | + |
| 233 | + |
| 234 | + |
| 235 | + |
| 236 | + |
| 237 | + |
| 238 | + |
| 239 | + |
| 240 | + |
| 241 | + |
| 242 | + |
| 243 | + |
| 244 | + |
| 245 | + |
| 246 | + |
| 247 | + |
0 commit comments