684. Redundant Connection #1242
-
|
Topics: In this problem, a tree is an undirected graph that is connected and has no cycles. You are given a graph that started as a tree with Return an edge that can be removed so that the resulting graph is a tree of Example 1:
Example 2:
Constraints:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
The Redundant Connection problem asks us to identify an edge in a graph that can be removed to turn the graph into a valid tree. A tree is an undirected graph that is connected and acyclic. We are given a graph that started as a tree but was modified by adding one extra edge. Our goal is to find and return this extra edge. Key Points
ApproachThe approach involves using Depth-First Search (DFS) to detect cycles:
Plan
Let's implement this solution in PHP: 684. Redundant Connection <?php
/**
* @param Integer[][] $edges
* @return Integer[]
*/
function findRedundantConnection($edges) {
$N = count($edges);
// Initialize adjacency list
$adjList = array_fill(0, $N, []);
foreach ($edges as $edge) {
$visited = array_fill(0, $N, false);
// Check if adding the edge creates a cycle
if ($this->isConnected($edge[0] - 1, $edge[1] - 1, $visited, $adjList)) {
return $edge;
}
// Add the edge to the adjacency list
$adjList[$edge[0] - 1][] = $edge[1] - 1;
$adjList[$edge[1] - 1][] = $edge[0] - 1;
}
return [];
}
/**
* Helper function to perform DFS and check connectivity
*
* @param $src
* @param $target
* @param $visited
* @param $adjList
* @return bool
*/
private function isConnected($src, $target, &$visited, &$adjList) {
$visited[$src] = true;
if ($src === $target) {
return true;
}
foreach ($adjList[$src] as $adj) {
if (!$visited[$adj]) {
if ($this->isConnected($adj, $target, $visited, $adjList)) {
return true;
}
}
}
return false;
}
// Example usage:
$edges1 = [[1,2],[1,3],[2,3]];
$edges2 = [[1,2],[2,3],[3,4],[1,4],[1,5]];
print_r(findRedundantConnection($edges1)) . "\n"; // Output: [2,3]
print_r(findRedundantConnection($edges2)) . "\n"; // Output: [1,4]
?>Explanation:
Example WalkthroughExample 1:Input: Steps:
Output: Example 2:Input: Steps:
Output: Time Complexity
Output for ExamplesExample 1:Input: Example 2:Input: The problem can be efficiently solved using a DFS-based approach to detect cycles. This method dynamically builds the graph and checks for redundant edges at each step. The solution ensures correctness by adhering to the problem constraints and outputs the edge that forms a cycle and occurs last in the input. |
Beta Was this translation helpful? Give feedback.
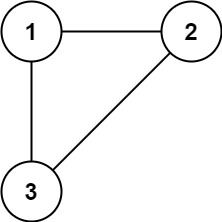
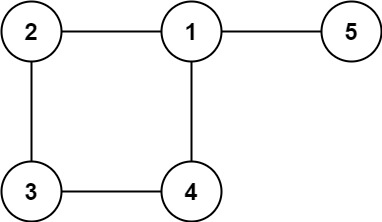
The Redundant Connection problem asks us to identify an edge in a graph that can be removed to turn the graph into a valid tree. A tree is an undirected graph that is connected and acyclic. We are given a graph that started as a tree but was modified by adding one extra edge. Our goal is to find and return this extra edge.
Key Points
Approach
The approach involves using Depth-First Search (DFS) to detect cyc…