3100. Water Bottles II

[mah-shamim]

Topics: Math, Simulation, Weekly Contest 391

You are given two integers numBottles and numExchange.

numBottles represents the number of full water bottles that you initially have. In one operation, you can perform one of the following operations:

• Drink any number of full water bottles turning them into empty bottles.
• Exchange numExchange empty bottles with one full water bottle. Then, increase numExchange by one.

Note that you cannot exchange multiple batches of empty bottles for the same value of numExchange. For example, if numBottles == 3 and numExchange == 1, you cannot exchange 3 empty water bottles for 3 full bottles.

Return the maximum number of water bottles you can drink.

Example 1:

• Input: numBottles = 13, numExchange = 6
• Output: 15
• Explanation: The table above shows the number of full water bottles, empty water bottles, the value of numExchange, and the number of bottles drunk.

Example 2:

• Input: numBottles = 10, numExchange = 3
• Output: 13
• Explanation: The table above shows the number of full water bottles, empty water bottles, the value of numExchange, and the number of bottles drunk.

Constraints:

• 1 <= numBottles <= 100
• 1 <= numExchange <= 100

Hint:

1. Simulate the process step by step. At each step, drink numExchange bottles of water then exchange them for a full bottle. Keep repeating this step until you cannot exchange bottles anymore.

[mah-shamim]

We need to find the maximum number of water bottles that can be drunk by strategically using the exchange operation.

Approach

The key insight is that we should exchange empty bottles for full ones whenever possible, and each exchange increases the exchange rate for future exchanges. The optimal strategy is:

1. Drink all available full bottles to get empty bottles
2. Exchange empty bottles for full bottles when we have enough
3. Repeat until no more exchanges are possible

We will simulate this process step by step:

• Start with initial full bottles
• Drink them all to get empty bottles
• Exchange empty bottles for full ones when possible
• Each exchange increases the exchange rate
• Continue until we can't exchange anymore

Let's implement this solution in PHP: 3100. Water Bottles II

<?php
/**
 * @param Integer $numBottles
 * @param Integer $numExchange
 * @return Integer
 */
function maxBottlesDrunk($numBottles, $numExchange) {
    $totalDrunk = 0;
    $emptyBottles = 0;
    $currentExchange = $numExchange;

    while ($numBottles > 0) {
        // Drink all current full bottles
        $totalDrunk += $numBottles;
        $emptyBottles += $numBottles;
        $numBottles = 0;

        // Exchange empty bottles for full ones if possible
        while ($emptyBottles >= $currentExchange) {
            $emptyBottles -= $currentExchange;
            $numBottles++;
            $currentExchange++;
        }
    }

    return $totalDrunk;
}

// Test cases
echo maxBottlesDrunk(13, 6) . "\n"; // 15
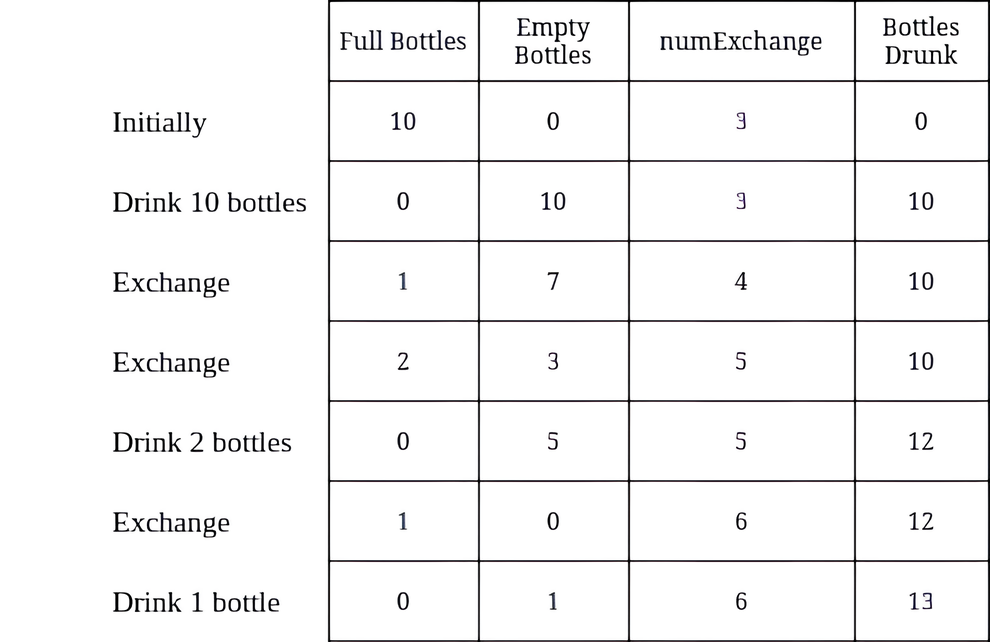
echo maxBottlesDrunk(10, 3) . "\n"; // 13
?>

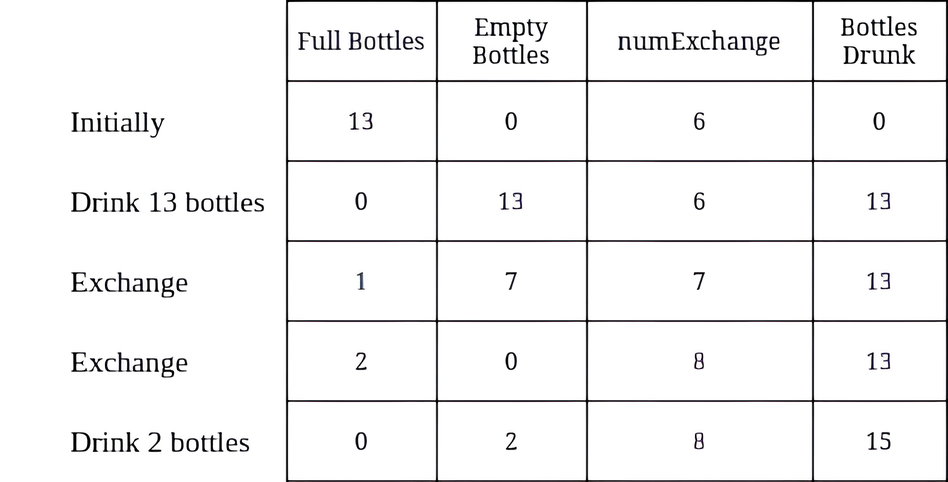
Explanation:

Let's trace through Example 1: numBottles = 13, numExchange = 6

1. Initial state: 13 full bottles, 0 empty, exchange rate = 6
2. Drink all: Drink 13 bottles → total = 13, empty = 13, full = 0
3. Exchange: 13 empty ≥ 6 exchange rate → exchange 6 empty for 1 full → empty = 7, full = 1, exchange rate = 7
4. Drink: Drink 1 bottle → total = 14, empty = 8, full = 0
5. Exchange: 8 empty ≥ 7 exchange rate → exchange 7 empty for 1 full → empty = 1, full = 1, exchange rate = 8
6. Drink: Drink 1 bottle → total = 15, empty = 2, full = 0
7. Stop: 2 empty < 8 exchange rate → cannot exchange further

Final result: 15 bottles drunk

The algorithm efficiently simulates this optimal strategy by always drinking all available bottles first, then exchanging as much as possible, repeating until no more exchanges can be made.

Time Complexity: O(n) where n is the number of bottles
Space Complexity: O(1) using only a few variables

[kovatz]

Thanks for solving the problem of "Water Bottles II"

[mah-shamim]

Thanks