778. Swim in Rising Water #2256
-
|
Topics: You are given an It starts raining, and water gradually rises over time. At time You can swim from a square to another 4-directionally adjacent square if and only if the elevation of both squares individually are at most Return the minimum time until you can reach the bottom right square Example 1:
Example 2:
Constraints:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to determine the minimum time required to swim from the top-left corner (0, 0) to the bottom-right corner (n-1, n-1) of an n x n grid, where each cell has a unique elevation. The water level rises over time, and at time Approach
Let's implement this solution in PHP: 778. Swim in Rising Water <?php
/**
* @param Integer[][] $grid
* @return Integer
*/
function swimInWater($grid) {
$n = count($grid);
$left = 0;
$right = $n * $n - 1;
while ($left < $right) {
$mid = intval(($left + $right) / 2);
if (canReach($grid, $mid, $n)) {
$right = $mid;
} else {
$left = $mid + 1;
}
}
return $left;
}
/**
* @param $grid
* @param $time
* @param $n
* @return bool
*/
private function canReach($grid, $time, $n) {
if ($grid[0][0] > $time) {
return false;
}
$visited = array_fill(0, $n, array_fill(0, $n, false));
$queue = new SplQueue();
$queue->enqueue([0, 0]);
$visited[0][0] = true;
$directions = [[0, 1], [1, 0], [0, -1], [-1, 0]];
while (!$queue->isEmpty()) {
list($i, $j) = $queue->dequeue();
if ($i == $n - 1 && $j == $n - 1) {
return true;
}
foreach ($directions as $dir) {
$x = $i + $dir[0];
$y = $j + $dir[1];
if ($x >= 0 && $x < $n && $y >= 0 && $y < $n && !$visited[$x][$y] && $grid[$x][$y] <= $time) {
$visited[$x][$y] = true;
$queue->enqueue([$x, $y]);
}
}
}
return false;
}
// Test cases
$grid1 = [[0,2],[1,3]];
echo swimInWater($grid1) . PHP_EOL; // 3
$grid2 = [
[0,1,2,3,4],
[24,23,22,21,5],
[12,13,14,15,16],
[11,17,18,19,20],
[10,9,8,7,6]
];
echo swimInWater($grid2) . PHP_EOL; // 16
?>Explanation:
This approach efficiently narrows down the possible time values using binary search and checks path feasibility using BFS, ensuring optimal performance even for the upper constraint limits. |
Beta Was this translation helpful? Give feedback.
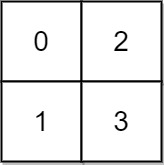
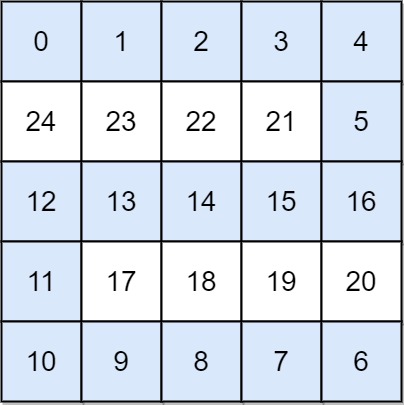
We need to determine the minimum time required to swim from the top-left corner (0, 0) to the bottom-right corner (n-1, n-1) of an n x n grid, where each cell has a unique elevation. The water level rises over time, and at time
t, any cell with an elevation ≤tis reachable. We can move to adjacent cells (up, down, left, right) only if both the current and target cells have elevations ≤t.Approach
tsuch that there exists a path from (0, 0) to (n-1, n-1) where all cells in the path have elevations ≤t.