Tutorial: Advection Equation with data driven DeepONet¶
+++⚠️ Before starting:¶
We assume you are already familiar with the concepts covered in the Getting started with PINA tutorials. If not, we strongly recommend reviewing them before exploring this advanced topic.
+
In this tutorial, we demonstrate how to solve the advection operator learning problem using DeepONet. We follow the original formulation of Lu et al. in DeepONet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operator.
We begin by importing the necessary modules.
+## routine needed to run the notebook on Google Colab
+try:
+ import google.colab
+
+ IN_COLAB = True
+except:
+ IN_COLAB = False
+if IN_COLAB:
+ !pip install "pina-mathlab[tutorial]"
+ # get the data
+ !mkdir "data"
+ !wget "https://github.com/mathLab/PINA/raw/refs/heads/master/tutorials/tutorial24/data/advection_input_testing.pt" -O "data/advection_input_testing.pt"
+ !wget "https://github.com/mathLab/PINA/raw/refs/heads/master/tutorials/tutorial24/data/advection_input_training.pt" -O "data/advection_input_training.pt"
+ !wget "https://github.com/mathLab/PINA/raw/refs/heads/master/tutorials/tutorial24/data/advection_output_testing.pt" -O "data/advection_output_testing.pt"
+ !wget "https://github.com/mathLab/PINA/raw/refs/heads/master/tutorials/tutorial24/data/advection_output_training.pt" -O "data/advection_output_training.pt"
+
+import matplotlib.pyplot as plt
+import torch
+import warnings
+from functools import partial
+
+
+from pina import Trainer, LabelTensor
+from pina.model import FeedForward, DeepONet
+from pina.solver import SupervisedSolver
+from pina.problem.zoo import SupervisedProblem
+from pina.loss import LpLoss
+
+warnings.filterwarnings("ignore")
+Advection problem and data preparation¶
We consider the 1D advection equation +$$ +\frac{\partial u}{\partial t} + \frac{\partial u}{\partial x} = 0, +\quad x \in [0,2], \; t \in [0,1], +$$ +with periodic boundary conditions. The initial condition is chosen as a Gaussian pulse centered at a random location +$\mu \sim U(0.05, 1)$ and with variance $\sigma^2 = 0.02$: +$$ +u_0(x) = \frac{1}{\sqrt{\pi\sigma^2}} e^{-\frac{(x - \mu)^2}{2\sigma^2}}, +\quad x \in [0,2]. +$$
+Our goal is to learn the operator
+$$
+\mathcal{G}: u_0(x) \mapsto u(x, t = \delta) = u_0(x - \delta),
+$$
+with $\delta = 0.5$ for this tutorial. In practice, this means learning a mapping from the initial condition to the solution at a fixed later time.
+The dataset therefore consists of trajectories where inputs are initial profiles and outputs are the same profiles shifted by $\delta$.
The data has shape [T, Nx, D], where:
-
+
T— number of trajectories (100 for training, 1000 for testing),
+Nx— number of spatial grid points (fixed at 100),
+D = 1— single scalar field valueu.
+
We now load the dataset and visualize sample trajectories.
+# loading training data
+data_0_training = LabelTensor(
+ torch.load("data/advection_input_training.pt", weights_only=False),
+ labels="u0",
+)
+data_dt_training = LabelTensor(
+ torch.load("data/advection_output_training.pt", weights_only=False),
+ labels="u",
+)
+
+# loading testing data
+data_0_testing = LabelTensor(
+ torch.load("data/advection_input_testing.pt", weights_only=False),
+ labels="u0",
+)
+data_dt_testing = LabelTensor(
+ torch.load("data/advection_output_testing.pt", weights_only=False),
+ labels="u",
+)
+The data are loaded, let's visualize a few of the initial conditions!
+# storing the discretization in space:
+Nx = data_0_training.shape[1]
+
+for idx, i in enumerate(torch.randint(0, data_0_training.shape[0] - 1, (3,))):
+ u0 = data_0_training[int(i)].extract("u0")
+ u = data_dt_training[int(i)].extract("u")
+ x = torch.linspace(
+ 0, 2, Nx
+ ) # the discretization in the spatial dimension is fixed
+ plt.subplot(3, 1, idx + 1)
+ plt.plot(x, u0.flatten(), label=rf"$u_0(x)$")
+ plt.plot(x, u.flatten(), label=rf"$u(x, t=\delta)$")
+ plt.xlabel(rf"$x$")
+ plt.tight_layout()
+ plt.legend()
+Great — we have generated a traveling wave and visualized a few samples. Next, we will use this data to train a DeepONet.
DeepONet¶
The standard DeepONet architecture consists of two subnetworks: a branch network and a trunk network (see figure below).
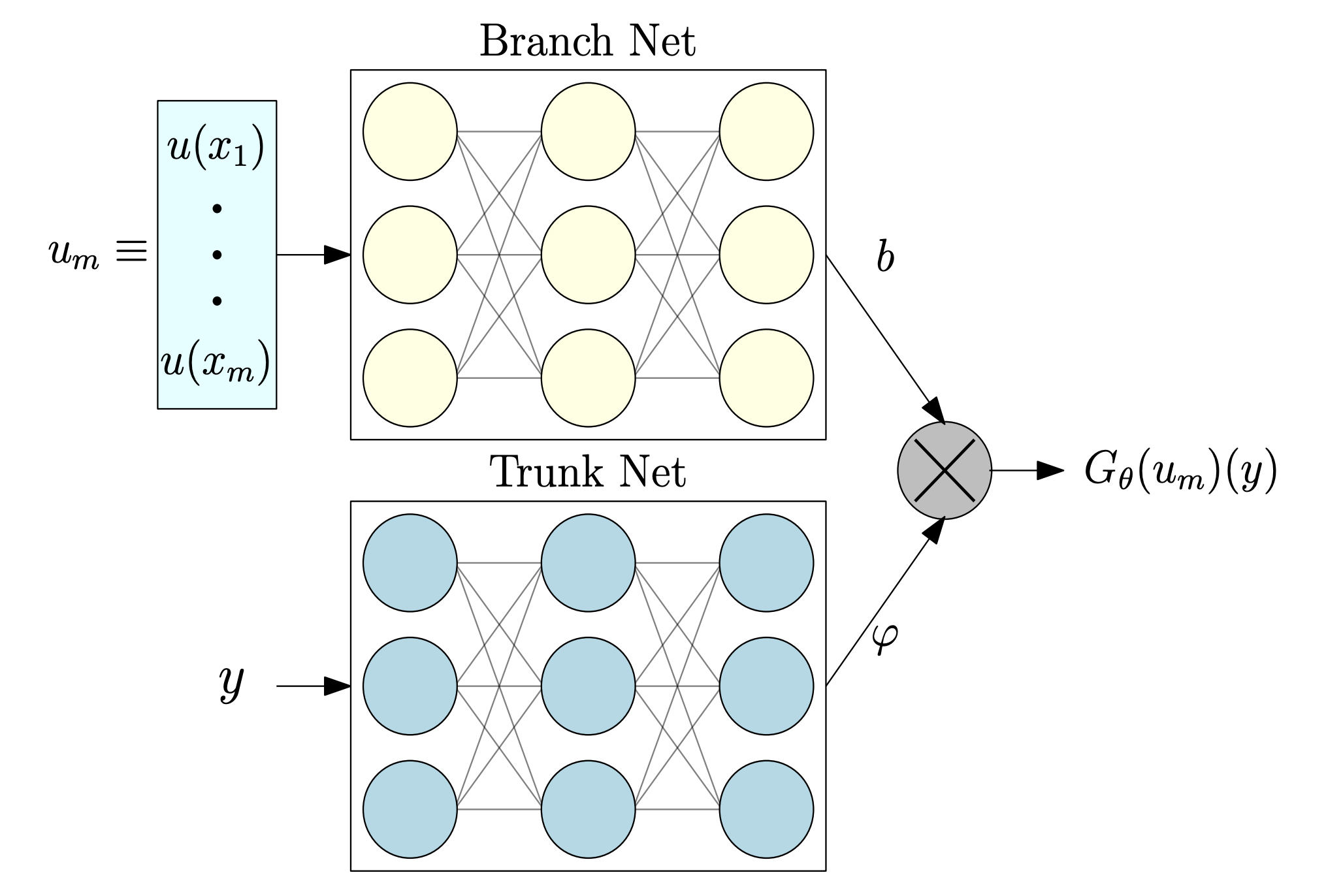 +
+In our setting:
+-
+
- The branch network receives the initial condition of each trajectory, with input shape
[B, Nx]— whereBis the batch size andNxthe spatial discretization points of the field at ( t = 0 ).
+ - The trunk network takes input of shape
[B, 1], corresponding to the location at which we evaluate the solution (in this 1D case, the spatial coordinate).
+
Together, these networks learn the mapping from the initial field to the solution at a later time.
+We now define and train the model for the advection problem.
+problem = SupervisedProblem(
+ input_=data_0_training,
+ output_=data_dt_training,
+ input_variables=data_0_training.labels,
+ output_variables=data_dt_training.labels,
+)
+We now proceede to create the trunk and branch networks.
+# create Trunk model
+class TrunkNet(torch.nn.Module):
+ def __init__(self, **kwargs):
+ super().__init__()
+ self.trunk = FeedForward(**kwargs)
+
+ def forward(self, x):
+ t = (
+ torch.zeros(size=(x.shape[0], 1), requires_grad=False) + 0.5
+ ) # create an input of only 0.5
+ return self.trunk(t)
+
+
+# create Branch model
+class BranchNet(torch.nn.Module):
+ def __init__(self, **kwargs):
+ super().__init__()
+ self.branch = FeedForward(**kwargs)
+
+ def forward(self, x):
+ return self.branch(x.flatten(1))
+The TrunkNet is implemented as a standard FeedForward network with a slightly modified forward method. In this case, the trunk network simply outputs a tensor filled with the value (0.5), repeated for each trajectory — corresponding to evaluating the solution at time (t = 0.5).
The BranchNet is also a FeedForward network, but its forward pass first flattens the input along the last dimension. This produces a vector of length Nx, representing the sampled initial condition at the sensor locations.
With both subnetworks defined, we can now instantiate the DeepONet model using the DeepONet class from pina.model.
# initialize truck and branch net
+trunk = TrunkNet(
+ layers=[256] * 4,
+ output_dimensions=Nx,
+ input_dimensions=1, # time variable dimension
+ func=torch.nn.ReLU,
+)
+branch = BranchNet(
+ layers=[256] * 4,
+ output_dimensions=Nx,
+ input_dimensions=Nx, # spatial variable dimension
+ func=torch.nn.ReLU,
+)
+
+# initialize the DeepONet model
+model = DeepONet(
+ branch_net=branch,
+ trunk_net=trunk,
+ input_indeces_branch_net=["u0"],
+ input_indeces_trunk_net=["u0"],
+ reduction="id",
+ aggregator="*",
+)
+The aggregation and reduction functions combine the outputs of the branch and trunk networks. In this example, their outputs are multiplied element-wise, and no reduction is applied — meaning the final output has the same dimensionality as each network’s output.
+We train the model using a SupervisedSolver with an MSE loss. Below, we first define the solver and then the trainer used to run the optimization.
# define solver
+solver = SupervisedSolver(problem=problem, model=model)
+
+# define the trainer and train
+trainer = Trainer(
+ solver=solver, max_epochs=200, enable_model_summary=False, accelerator="cpu"
+)
+trainer.train()
+💡 Tip: For seamless cloud uploads and versioning, try installing [litmodels](https://pypi.org/project/litmodels/) to enable LitModelCheckpoint, which syncs automatically with the Lightning model registry. ++
GPU available: False, used: False ++
TPU available: False, using: 0 TPU cores ++
`Trainer.fit` stopped: `max_epochs=200` reached. ++
Let's see the final train and test errors:
+# the l2 error
+l2 = LpLoss()
+
+with torch.no_grad():
+ train_err = l2(trainer.solver(data_0_training), data_dt_training)
+ test_err = l2(trainer.solver(data_0_testing), data_dt_testing)
+
+print(f"Training error: {float(train_err.mean()):.2%}")
+print(f"Testing error: {float(test_err.mean()):.2%}")
+Training error: 0.87% +Testing error: 1.58% ++
We can see that the testing error is slightly higher than the training one, maybe due to overfitting. We now plot some results trajectories.
+for i in [1, 2, 3]:
+ plt.subplot(3, 1, i)
+ plt.plot(
+ torch.linspace(0, 2, Nx),
+ solver(data_0_training)[10 * i].detach().flatten(),
+ label=r"$u_{NN}$",
+ )
+ plt.plot(
+ torch.linspace(0, 2, Nx),
+ data_dt_training[10 * i].extract("u").flatten(),
+ label=r"$u$",
+ )
+ plt.xlabel(r"$x$")
+ plt.legend(loc="upper right")
+ plt.show()
+As we can see, they are barely indistinguishable. To better understand the difference, we now plot the residuals, i.e. the difference of the exact solution and the predicted one.
+for i in [1, 2, 3]:
+ plt.subplot(3, 1, i)
+ plt.plot(
+ torch.linspace(0, 2, Nx),
+ data_dt_training[10 * i].extract("u").flatten()
+ - solver(data_0_training)[10 * i].detach().flatten(),
+ label=r"$u - u_{NN}$",
+ )
+ plt.xlabel(r"$x$")
+ plt.tight_layout()
+ plt.legend(loc="upper right")
+What's Next?¶
We have seen a simple example of using DeepONet to learn the advection operator. This only scratches the surface of what neural operators can do. Here are some suggested directions to continue your exploration:
-
+
Train on more complex PDEs: Extend beyond the advection equation to more challenging operators, such as diffusion or nonlinear conservation laws.
+
+Increase training scope: Experiment with larger datasets, deeper networks, and longer training schedules to unlock the full potential of neural operator learning.
+
+Generalize to the full advection operator: Train the model to learn the general operator $\mathcal{G}_t: u_0(x) \mapsto u(x,t) = u_0(x - t)$ so the network predicts solutions for arbitrary times, not just a single fixed horizon.
+
+Investigate architectural variations: Compare different operator learning architectures (e.g., Fourier Neural Operators, Physics-Informed DeepONets) to see how they perform on similar problems.
+
+...and much more!: From adding noise robustness to testing on real scientific datasets, the space of possibilities is wide open.
+
+
For more resources and tutorials, check out the PINA Documentation.
+ -#
-#  -#
-#