Problem with lumped model or characteristic of soft pack battery?

[RobinBluehub]

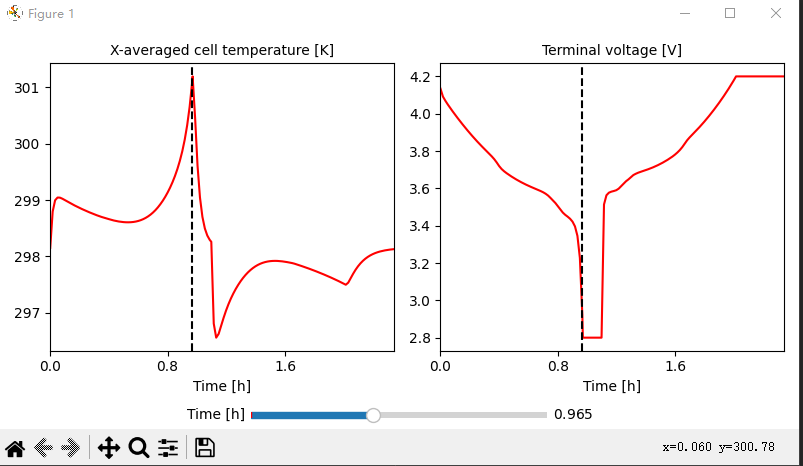
When I used the "Mohtat2020" parameter set to study the effect of temperature on battery life, I found that the temperature of the pouch battery dropped too fast during the constant voltage discharge stage, even lower than room temperature 298.15K. Since I have not done any related research on pouch batteries Experiment, this phenomenon confuses me. Thank you for taking the time to respond.

Code：
`import pybamm
import numpy as np
import matplotlib.pyplot as plt

pybamm.set_logging_level("NOTICE")
options = {
"thermal": "lumped",
}
model = pybamm.lithium_ion.DFN(options=options)
parameter_values = pybamm.ParameterValues("Mohtat2020")

param = model.param
esoh_solver = pybamm.lithium_ion.ElectrodeSOHSolver(parameter_values,param)
Vmin = 3.0
Vmax = 4.2
Cn = parameter_values.evaluate(param.n.cap_init)
Cp = parameter_values.evaluate(param.p.cap_init)
n_Li_init = parameter_values.evaluate(param.n_Li_particles_init)
inputs={"V_min": Vmin, "V_max": Vmax,"C_n": Cn, "C_p": Cp, "n_Li": n_Li_init}
esoh_sol = esoh_solver.solve(inputs)
print(f"Initial negative electrode SOC: {esoh_sol['x_100'].data[0]:.3f}")
print(f"Initial positive electrode SOC: {esoh_sol['y_100'].data[0]:.3f}")
c_n_max = parameter_values.evaluate(param.n.prim.c_max)
c_p_max = parameter_values.evaluate(param.p.prim.c_max)
parameter_values.update({
"Initial concentration in negative electrode [mol.m-3]": esoh_sol["x_100"].data[0] * c_n_max,
"Initial concentration in positive electrode [mol.m-3]": esoh_sol["y_100"].data[0] * c_p_max,
})

solver = pybamm.CasadiSolver()
var_pts = {"x_n": 30, "x_s": 30, "x_p": 30, "r_n": 20, "r_p": 20}
experiment=pybamm.Experiment([(
"Discharge at 1C until 2.8V",
"Hold at 2.8V until C/50",
"Charge at 1C until 4.2V",
"Hold at 4.2 V until C/50",
)]*1)
sim = pybamm.Simulation(model,parameter_values=parameter_values,experiment=experiment,solver=solver,var_pts=var_pts)
sol_1=sim.solve(initial_soc=1)
sim.plot(["X-averaged cell temperature [K]","Terminal voltage [V]"])`

[rtimms]

You can plot all the heat source terms by doing sim.plot(["X-averaged Ohmic heating [W.m-3]", "X-averaged irreversible electrochemical heating [W.m-3]", "X-averaged reversible heating [W.m-3]", "X-averaged cell temperature [K]","Terminal voltage [V]"]). During the CV hold at the end of the discharge the reversible term goes very negative. Might be worth taking a look at the paper to check how robust the parameterization of that term was.

[RobinBluehub]

Which paper are you referring to?

[rtimms]

Mohtat 2020