Question on Link Prediction Experiment Design

[cemunds]

Hi, I would appreciate a second opinion on whether my experiment design is sound.

I have a dataset of let's say 10 independent graphs and want to do link prediction in an inductive setting, where I train my model to recognize missing edges using some of the graphs and then apply it to a different set of graphs. I also want to evaluate how the model responds to varying amounts of edges being missing. So, I start by reserving 10% of the edges in each graph for the supervision signal (while also sampling a corresponding amount of negative edges) and keep 90% for message passing. Afterwards I train another model with 20% of the edges for supervision and 80% for message passing and so on, until I reach 90% of edges for supervision and 10% for message passing.

This is a plot of some preliminary results I got:

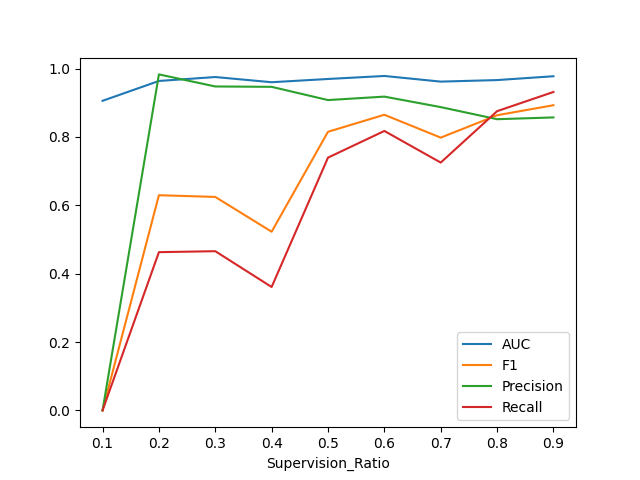
It seems like using only 10% of the edges as supervision signal is too few, as my precision and recall is 0. What surprises me is how the metrics can be in the range of 80%-90% while using 90% of the edges for supervision and keeping only 10% for message passing. In fact, I can even go as far as to use 99% of the edges for supervision and only 1% for message passing and still achieve a precision, recall and AUC in the range of 85%-97%.

This makes me wonder if there is some kind of overfitting involved, where the model memorizes the missing edges, but I wouldn't know how that should be possible given that my training and test set consist of entirely independent graphs. Could it really be that the relational information is somewhat irrelevant to my particular prediction task and the model actually just benefits from having a bigger supervision signal, or can someone spot a flaw in my experiment design that I'm not seeing? I have yet to test what happens if I simply use a MLP to embed the nodes and don't make use of any relational information at all.

I would greatly appreciate any feedback.

[EdisonLeeeee]

Hi @cemunds , I found your observations quite interesting! They are also consistent with some recent work [1][2], where dropping/masking a large proportion of edges in a graph can still result in good GNN performance.

Here are my understandings:

• There are indeed several irrelevant or even noisy edges in a graph.
• The node features are strong enough that a few connections are sufficient to train a good GNN.

Currently, I haven't delved into this yet and provided a theoretical investigation. Additionally, testing the performance of using an MLP to embed the nodes without any relational information would be an interesting comparison to make.

Hope my answer can help you.

[1] DropEdge: Towards Deep Graph Convolutional Networks on Node Classification, https://arxiv.org/abs/1907.10903
[2] MaskGAE: Masked Graph Modeling Meets Graph Autoencoders, https://arxiv.org/abs/2205.10053