Leaf-to-root message passing over dags, one "level" at a time #7171
-
|
A little background: job scheduling is in important component of cloud orchestration tools such as Apache Spark, and a good scheduling algorithm can greatly improve a cluster's efficiency. In Spark, jobs are dags of "stages," where each stage is some operation, e.g map or reduce. This 2019 paper proposed a method of learning scheduling algorithms, taking into account the dependencies between the stages unlike many traditional schedulers. They frame job scheduling as an RL problem, and they use GNN's to encode the state of the cluster. I am re-implementing their codebase, which uses Tensorflow 1.x. Their message passing scheme is unconventional, as far as I can tell: for each dag, they pass messages from its leaves to its root, making computations on only one "level" of the dag at each step. That is, suppose we have the dag They achieve this message passing one "level" at a time by doing some complicated masking. Once the masks are computed, they are used in this forward pass. They also set a max message passing depth Best, |
Beta Was this translation helpful? Give feedback.
Replies: 2 comments
-
|
One way to implement it in pyg is by using the masking approach you described in the paper. Further , checkout DAGNN which is a GNN built for DAGs. |
Beta Was this translation helpful? Give feedback.
-
|
Thanks to @wsad1, I was able to roughly replicate the original message passing using PyG (particularly import torch
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import subgraph
import networkx as nx
from networkx.drawing.nx_agraph import graphviz_layout
class CriticalPathConv(MessagePassing):
def __init__(self):
super().__init__(aggr="max", flow='target_to_source')
def forward(self, x, edge_index):
return self.propagate(edge_index, x=x)
conv = CriticalPathConv()
# simple dag structure
edge_index = torch.tensor([
[0, 0, 1, 2],
[1, 2, 3, 3]
])
# node weights that will contribute to CP length
x = torch.tensor([1, 3, 0, 2]).unsqueeze(-1)
x_orig = x.clone()
# use nx to obtain node levels
G = nx.DiGraph()
G.add_nodes_from(range(x.shape[0]))
G.add_edges_from(edge_index.T.numpy())
node_levels = list(nx.topological_generations(G))
# iterate through one level of the dag at a time, in reverse order
for l in reversed(range(1, len(node_levels))):
print(x.squeeze())
# include edges that touch nodes from this level and the level above
nodes_include = node_levels[l] + node_levels[l-1]
# obtain "masked" edge index, which only includes edges that touch the current level and its parents
level_edge_index = subgraph(nodes_include, edge_index, num_nodes=x.shape[0])[0]
# forward pass
x = x + conv(x, level_edge_index)
print(x.squeeze(), '<- node-weighted critical path length from each node')
nx.draw_networkx(
G,
node_color=['red'] + 3*['yellow'],
labels={i: x.item() for i, x in enumerate(x_orig)},
pos=graphviz_layout(G, prog='dot')
)Here is the output:
A couple notes:
|
Beta Was this translation helpful? Give feedback.
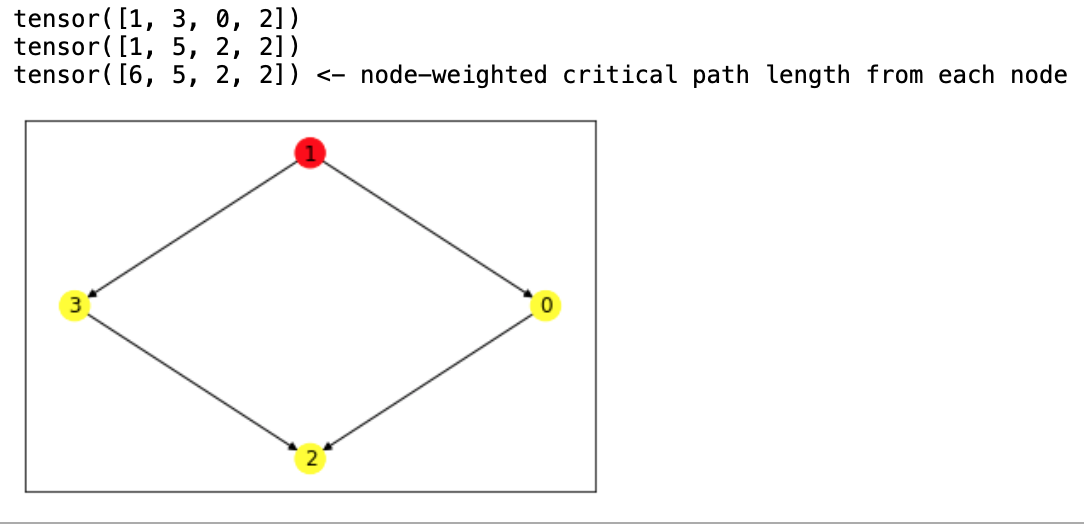
Thanks to @wsad1, I was able to roughly replicate the original message passing using PyG (particularly
subgraph) and NetworkX. To anyone else interested in this kind of message passing, here is a very simple example that calculates the critical path length (weighted by node values) of a dag starting from each node: