Embedding

Embedding

An embedding of a graph is an assignment of points in the plane to the vertices of the graph. To visualize a graph in its current embedding, see the DrawSimpleGraphs module or one of the Exporting functions.

A graph's embedding is part of the graph's data structure. See the Cache page of this Wiki.

Note: A graph's embedding is independent of its rotation system. See this entry for more detail.

Creating an Embedding

• embed(G) gives G the circular embedding.
• embed(G,method) gives G an embedding using one of the following methods:
  • :circular: vertices arranged in a circle.
  • :random: vertices placed at random locations.
  • :spring: model edges as springs and vertices are repelling bodies.
  • :spectral: coordinates based on eigenvectors for the 2nd and 3rd smallest eigenvalues.
  • :stress: attempt to place vertices so their geometric distance matches their graph-theoretic distance.
  • :combined: First do a :spring and then do a :stress embedding. Often gives attractive results.
  • :tutte: Given a list of vertices of be placed at the corners of a regular convex polygon, embed the other vertices at the center of mass of their neighbors. If no list is given, then use the graph's rotation system and select a largest face for the outside vertices.
• embed(G,d): d is a dictionary mapping vertices to [x,y] vectors (one-dimensional arrays).

Modification Functions

• transform(G,A,b): modify the embedding by applying an affine function to the coordinates.
• recenter(G): moves the center of the embedding to the origin.

The following functions affect how the graph is drawn in DrawSimpleGraphs:

• set_vertex_size(G,r): specify the radius of the circle we draw to represent a vertex (default is 6).
• get_vertex_size(G): returns the vertex drawing radius.
• set_line_color(G,color): specify the color for the vertex circles and edge line segments (default is "black").
• get_line_color(G): returns the line color.
• set_vertex_color(G,color): specify the color that fills in the vertex circles (default is "white").
• get_vertex_color(G): return the fill color.

Embedding Related Functions

• has_embedding(G): check if the graph has been given an embedding.
• remove_embedding(G): removed the graph's embedding from its internal data structure.
• getxy(G): return the dictionary mapping the vertices to [x,y] vectors.
• edge_length(G,e): return the distance between the end points of edge e.

Output Functions

These are marginally supported functions for output of the graph's embedding for use by other applications.

• graffle(G,file_name,radius): output a file to be opened by OmniGraffle.
• geogebra(G,file_name): output a Geogebra script file to draw this graph.
• tikz_file(G,file_name): output Tikz code that can be imported into LaTeX.

Examples

The following images were formed by applying an embedding to a graph G = Dodecahedron() followed by draw(G) (which requires the DrawSimpleGraphs module):

Tutte embedding

Calling G = Dodecahedron() automatically gives G the tutte embedding using a specific 3-cycle as the outer face: embed(G, :tutte, outside = [1, 9, 2]). Here is the result:

Spring embedding

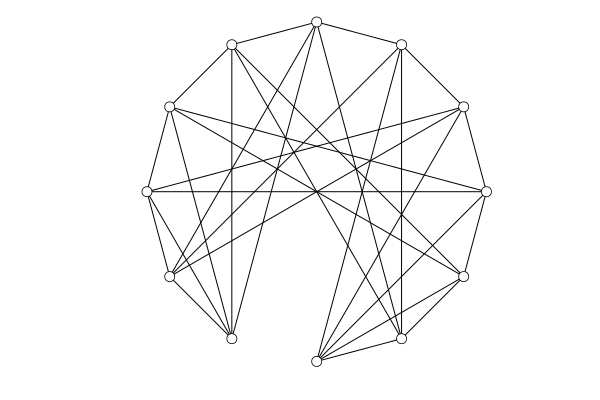
This is the result of embed(G,:spring):

Stress embedding

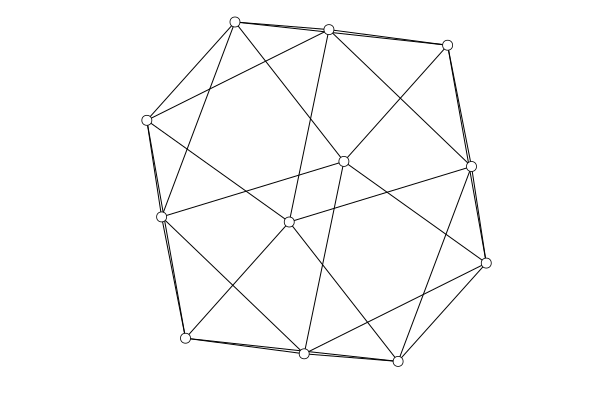
This is the result of embed(G,:stress) (which is similar to embed(G,:combined) because if followed a spring embedding):

Default (circular) embedding

This is the result of the base embed(G) which places all vertices around a circle: