|
8 | 8 | 某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。 |
9 | 9 |
|
10 | 10 |
|
11 | | -网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用;权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。 |
| 11 | +网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。 |
12 | 12 |
|
| 13 | +权值为正表示扣除了政府补贴后运输货物仍需支付的费用;权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。 |
13 | 14 |
|
14 | | -请找出从城市 1 到城市 n 的所有可能路径中,综合政府补贴后的最低运输成本。如果最低运输成本是一个负数,它表示在遵循最优路径的情况下,运输过程中反而能够实现盈利。 |
15 | 15 |
|
| 16 | +请找出从城市 1 到城市 n 的所有可能路径中,综合政府补贴后的最低运输成本。 |
| 17 | + |
| 18 | +如果最低运输成本是一个负数,它表示在遵循最优路径的情况下,运输过程中反而能够实现盈利。 |
16 | 19 |
|
17 | 20 | 城市 1 到城市 n 之间可能会出现没有路径的情况,同时保证道路网络中不存在任何负权回路。 |
18 | 21 |
|
|
41 | 44 | 1 3 5 |
42 | 45 | ``` |
43 | 46 |
|
44 | | -## 思路 |
| 47 | +## 背景 |
45 | 48 |
|
46 | 49 | 本题我们来系统讲解 Bellman_ford 队列优化算法 ,也叫SPFA算法(Shortest Path Faster Algorithm)。 |
47 | 50 |
|
48 | | -> SPFA的称呼来自 1994年西南交通大学段凡丁的论文,其实Bellman_ford 提出后不久 (20世纪50年代末期) 就有队列优化的版本,国际上不承认这个算法是是国内提出的。 所以国际上一般称呼 算法为 Bellman_ford 队列优化算法(Queue improved Bellman-Ford) |
| 51 | +> SPFA的称呼来自 1994年西南交通大学段凡丁的论文,其实Bellman_ford 提出后不久 (20世纪50年代末期) 就有队列优化的版本,国际上不承认这个算法是是国内提出的。 所以国际上一般称呼 该算法为 Bellman_ford 队列优化算法(Queue improved Bellman-Ford) |
49 | 52 |
|
50 | 53 | 大家知道以上来历,知道 SPFA 和 Bellman_ford 队列优化算法 指的都是一个算法就好。 |
51 | 54 |
|
|
72 | 75 |
|
73 | 76 | 用队列来记录。(其实用栈也行,对元素顺序没有要求) |
74 | 77 |
|
| 78 | +## 模拟过程 |
| 79 | + |
75 | 80 | 接下来来举例这个队列是如何工作的。 |
76 | 81 |
|
77 | 82 | 以示例给出的所有边为例: |
|
88 | 93 |
|
89 | 94 | 我们依然使用**minDist数组来表达 起点到各个节点的最短距离**,例如minDist[3] = 5 表示起点到达节点3 的最小距离为5 |
90 | 95 |
|
91 | | -初始化,起点为节点1, 起点到起点的最短距离为0,所以minDist[1] 为 0。 将节点1 加入队列 (下次松弛送节点1开始) |
| 96 | +初始化,起点为节点1, 起点到起点的最短距离为0,所以minDist[1] 为 0。 将节点1 加入队列 (下次松弛从节点1开始) |
92 | 97 |
|
93 | 98 | 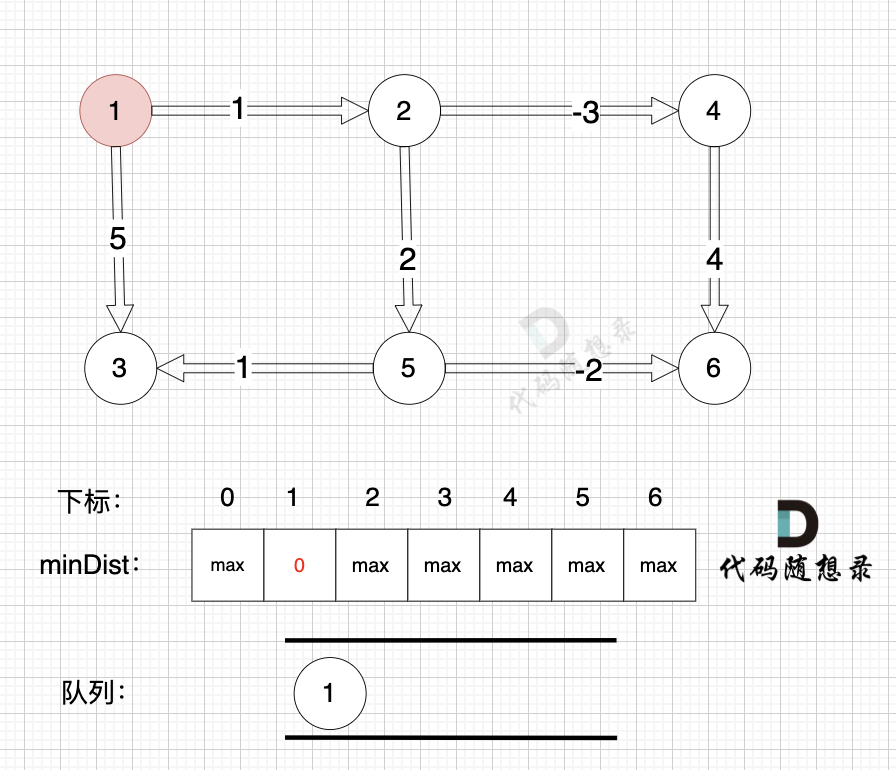 |
94 | 99 |
|
95 | 100 | ------------ |
96 | 101 |
|
97 | | -从队列里取出节点1,松弛节点1 作为出发点链接的边(节点1 -> 节点2)和边(节点1 -> 节点3) |
| 102 | +从队列里取出节点1,松弛节点1 作为出发点连接的边(节点1 -> 节点2)和边(节点1 -> 节点3) |
98 | 103 |
|
99 | 104 | 边:节点1 -> 节点2,权值为1 ,minDist[2] > minDist[1] + 1 ,更新 minDist[2] = minDist[1] + 1 = 0 + 1 = 1 。 |
100 | 105 |
|
101 | 106 | 边:节点1 -> 节点3,权值为5 ,minDist[3] > minDist[1] + 5,更新 minDist[3] = minDist[1] + 5 = 0 + 5 = 5。 |
102 | 107 |
|
103 | | -将节点2,节点3 加入队列,如图: |
| 108 | +将节点2、节点3 加入队列,如图: |
104 | 109 |
|
105 | 110 | 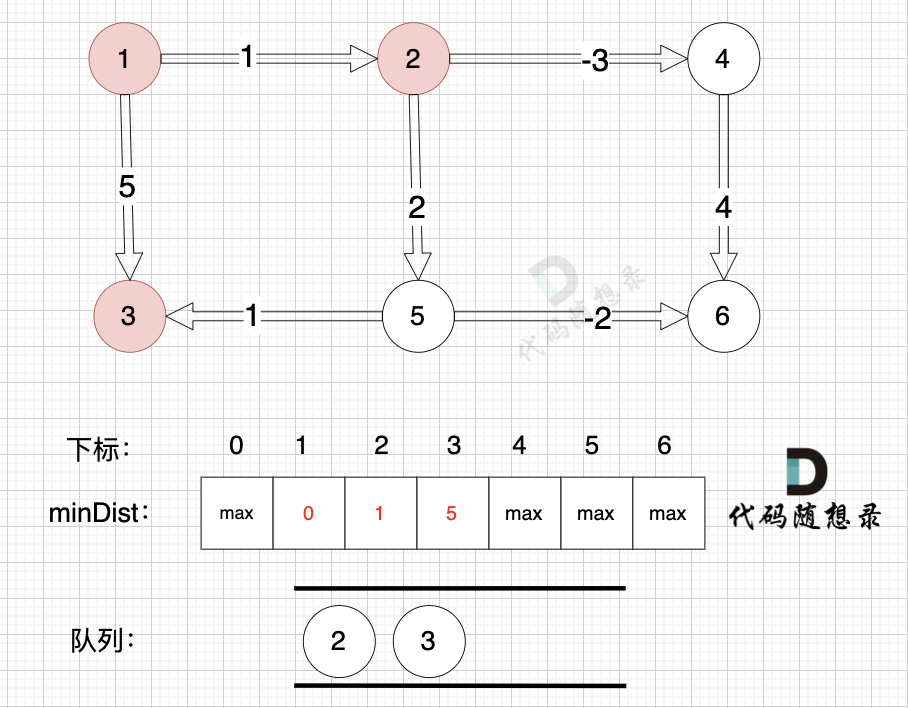 |
106 | 111 |
|
107 | 112 |
|
108 | 113 | ----------------- |
109 | 114 |
|
110 | 115 |
|
111 | | -从队列里取出节点2,松弛节点2 作为出发点链接的边(节点2 -> 节点4)和边(节点2 -> 节点5) |
| 116 | +从队列里取出节点2,松弛节点2 作为出发点连接的边(节点2 -> 节点4)和边(节点2 -> 节点5) |
112 | 117 |
|
113 | 118 | 边:节点2 -> 节点4,权值为1 ,minDist[4] > minDist[2] + (-3) ,更新 minDist[4] = minDist[2] + (-3) = 1 + (-3) = -2 。 |
114 | 119 |
|
|
123 | 128 | -------------------- |
124 | 129 |
|
125 | 130 |
|
126 | | -从队列里出去节点3,松弛节点3 作为出发点链接的边。 |
| 131 | +从队列里出去节点3,松弛节点3 作为出发点连接的边。 |
127 | 132 |
|
128 | 133 | 因为没有从节点3作为出发点的边,所以这里就从队列里取出节点3就好,不用做其他操作,如图: |
129 | 134 |
|
|
132 | 137 |
|
133 | 138 | ------------ |
134 | 139 |
|
135 | | -从队列中取出节点4,松弛节点4作为出发点链接的边(节点4 -> 节点6) |
| 140 | +从队列中取出节点4,松弛节点4作为出发点连接的边(节点4 -> 节点6) |
136 | 141 |
|
137 | 142 | 边:节点4 -> 节点6,权值为4 ,minDist[6] > minDist[4] + 4,更新 minDist[6] = minDist[4] + 4 = -2 + 4 = 2 。 |
138 | 143 |
|
139 | | -讲节点6加入队列 |
| 144 | +将节点6加入队列 |
140 | 145 |
|
141 | 146 | 如图: |
142 | 147 |
|
|
145 | 150 |
|
146 | 151 | --------------- |
147 | 152 |
|
148 | | -从队列中取出节点5,松弛节点5作为出发点链接的边(节点5 -> 节点3),边(节点5 -> 节点6) |
| 153 | +从队列中取出节点5,松弛节点5作为出发点连接的边(节点5 -> 节点3),边(节点5 -> 节点6) |
149 | 154 |
|
150 | 155 | 边:节点5 -> 节点3,权值为1 ,minDist[3] > minDist[5] + 1 ,更新 minDist[3] = minDist[5] + 1 = 3 + 1 = 4 |
151 | 156 |
|
|
157 | 162 |
|
158 | 163 |
|
159 | 164 |
|
160 | | -因为节点3,和 节点6 都曾经加入过队列,不用重复加入,避免重复计算。 |
| 165 | +因为节点3 和 节点6 都曾经加入过队列,不用重复加入,避免重复计算。 |
161 | 166 |
|
162 | 167 | 在代码中我们可以用一个数组 visited 来记录入过队列的元素,加入过队列的元素,不再重复入队列。 |
163 | 168 |
|
164 | 169 |
|
165 | 170 | -------------- |
166 | 171 |
|
167 | | -从队列中取出节点6,松弛节点6 作为出发点链接的边。 |
| 172 | +从队列中取出节点6,松弛节点6 作为出发点连接的边。 |
168 | 173 |
|
169 | 174 | 节点6作为终点,没有可以出发的边。 |
170 | 175 |
|
|
181 | 186 |
|
182 | 187 | 了解了大体流程,我们再看代码应该怎么写。 |
183 | 188 |
|
184 | | -在上面模拟过程中,我们每次都要知道 一个节点作为出发点 链接了哪些节点。 |
| 189 | +在上面模拟过程中,我们每次都要知道 一个节点作为出发点连接了哪些节点。 |
185 | 190 |
|
186 | 191 | 如果想方便知道这些数据,就需要使用邻接表来存储这个图,如果对于邻接表不了解的话,可以看 [kama0047.参会dijkstra堆](./kama0047.参会dijkstra堆.md) 中 图的存储 部分。 |
187 | 192 |
|
@@ -279,7 +284,7 @@ n为其他数值的时候,也是一样的。 |
279 | 284 |
|
280 | 285 | 并没有计算 出队列 和 入队列的时间消耗。 因为这个在不同语言上 时间消耗也是不一定的。 |
281 | 286 |
|
282 | | -以C++为例,以下两端代码理论上,时间复杂度都是 O(n) : |
| 287 | +以C++为例,以下两段代码理论上,时间复杂度都是 O(n) : |
283 | 288 |
|
284 | 289 | ```CPP |
285 | 290 | for (long long i = 0; i < n; i++) { |
@@ -316,7 +321,7 @@ SPFA(队列优化版Bellman_ford) 在理论上 时间复杂度更胜一筹 |
316 | 321 |
|
317 | 322 | 这里可能有录友疑惑,`while (!que.empty())` 队里里 会不会造成死循环? 例如 图中有环,这样一直有元素加入到队列里? |
318 | 323 |
|
319 | | -其实有环的情况,要看它是 正权回路 还是 负全回路。 |
| 324 | +其实有环的情况,要看它是 正权回路 还是 负权回路。 |
320 | 325 |
|
321 | 326 | 题目描述中,已经说了,本题没有 负权回路 。 |
322 | 327 |
|
|
0 commit comments