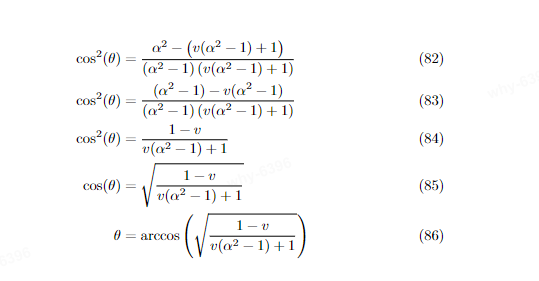Skip to content

Chillstepp/ChillSoftwareRenderer

BranchesTags

Repository files navigation

Chill Software Renderer

Tech

  • Shader-based programmable pipeline

  • Perspective-Correct Interpolation

  • Culling/Clipping

    • Sutherland-Hodgeman Clipping
    • Switchable Back/Front-Face Culling

  • [x]

  • Shader:

    • Phong
    • Blinn–Phong
    • PBR
    • Gouraud
    • Flat

  • Tangent Space Normal Mapping

  • Shadow

    • PCF
    • PCSS

  • AO

    • SSAO
    • HBAO

  • PBR(Metallic-Roughness Workflow)

  • Cubemap and Skybox

  • IBL

    • Diffuse IBL
    • Specular IBL

ShowCase

Blinn-Phong PBR + IBL
image-20240223183212808 image-20240309223909758

Tech Roadmap

Camera

  • 规定$CenterLocation - CameraLocation$ 作为向量规定为摄像机坐标系下z轴的正方向，即离摄像机越远的z值越大。
  • 右手坐标系
  • 注意当模型变换矩阵矩阵为$M$时，发现变换矩阵为$(M^{-1})^{T}$， 推导如下：

假设模型变换矩阵$M$,$\Delta ABC$的法线向量$n$,$\Delta ABC$上的任意点为$P1$和$P2,P1$和$P2$构成向量$P1-P2$, 满足$n^T(P1-P2)=0$。这里设$n$为列向量，$P1-P2$为列向量。

$P1P2$在变换后为$M(P1-P2)$,而因为有${n^T(M^{-1}M)(P1-P2)}=0$,

即$(n^TM^{-1})[M(P1-P2)]=0$,因此新的法向量应为$(n^TM^{-1})^T=(M^{-1})^Tn$

透视矫正 Perspective-Correct Interpolation

Before After
image-20240715105533773 image-20240715105559561

原因在于：用屏幕坐标插值这个行为是错误的

我们希望计算出，当屏幕空间上的插值比例为$\frac{m}{1-m}$时在世界空间中他们之间的真正比例是多少，我们设其为$\frac{n}{1-n}$，尝试计算$n$和$m$之间的关系:

$$ \frac{n}{1-n}=\frac{|AG|}{|BK|}=\frac{|A^{\prime}P^{\prime}|\frac{Z_{1}}{c}}{|B^{\prime}P^{\prime}|\frac{Z_{2}}{c}}=\frac{mZ_{1}}{(1-m)Z_{2}}\\frac{1}{n}-1=\frac{(1-m)Z_{2}}{mZ_{1}}\n=\frac{mZ_{1}}{(1-m)Z_{2}+mZ_{1}} $$

考虑当插值时:

$$ \begin{aligned} Z_{n}& =(1-n)Z_{1}+nZ_{2} \\ &=\frac{(1-m)Z_{2}}{(1-m)Z_{2}+mZ_{1}}Z_{1}+\frac{mZ_{1}}{(1-m)Z_{2}+mZ_{1}}Z_{2} \\ &=\frac{Z_1Z_2}{(1-m)Z_2+mZ_1} \\ &=\frac{1}{\frac{1-m}{Z_1}+\frac{m}{Z_2}} \end{aligned} $$

推广到3维：

$$ Z_n=\frac{1}{\frac{1-u-v}{Z_1}+\frac{u}{Z_2}+\frac{v}{Z_3}} $$

实现：

static Vec3f PerspectiveCorrectInterpolation(const std::vector<Vec4f> &HomogeneousCoord, Vec3f LinearInterpBaryCoord) {
    Vec3f CorrectBaryCoord;
    for (int i = 0; i < 3; i++)
    {
        CorrectBaryCoord.raw[i] = LinearInterpBaryCoord.raw[i] / HomogeneousCoord[i].w;
    }

    float Z_n = 1.0f / (CorrectBaryCoord.x + CorrectBaryCoord.y + CorrectBaryCoord.z);
    CorrectBaryCoord *= Z_n;

    return CorrectBaryCoord;
};

剔除 Culling

  • 视锥剔除：AABB Box 和 View AABB 无相交则不渲染
  • 背面剔除: 三角形法线方向和相机观察方向夹角小于90°(即$cos(\theta)>0$)则不进行渲染

实现：

for(int i=0;i<model->nfaces();i++)
{
    const std::vector<int>& face = model->getface(i);
    Vec3f WorldCoords[3];
    for(int j=0;j<3;j++)
    {
        WorldCoords[j] = model->getvert(i, j);
    }
    Vec3f ScreenCoords[3];
    for(int j=0;j<3;j++)
    {
        auto Mat4x1_Vertex = Shader->vertex(i, j);
        ScreenCoords[j] = {Mat4x1_Vertex.raw[0][0], Mat4x1_Vertex.raw[1][0], Mat4x1_Vertex.raw[2][0]};
    }
    Vec3f tri_normal = (WorldCoords[2]-WorldCoords[0])^(WorldCoords[1]-WorldCoords[0]);
    if(tri_normal.normlize() * (WorldCoords[0] - Eye) >= 0) //back face culling
    {
        triangle(model,ScreenCoords, image2,ZBuffer,Shader);
    }
}

裁剪 Sutherland-Hodgeman Clipping

当一个物体跨越Viewport时，不进行裁剪会出现很多错乱现象，本人在渲染天空盒时出现了很多错误现象，再进行裁切后正常

Suherland-Hodeman多边形裁剪算法，依次对六个面进行裁剪即可。

static std::vector<VertexOut> SutherlandHodmanClip(const std::vector<VertexOut>& InVertex)
{
    bool AllVertexInsideOfCVV = std::all_of(InVertex.begin(), InVertex.end(), [](const VertexOut& In){
        return std::abs(In.ClipSpaceCoord.x) <= std::abs(In.ClipSpaceCoord.w)
            && std::abs(In.ClipSpaceCoord.y) <= std::abs(In.ClipSpaceCoord.w)
            && std::abs(In.ClipSpaceCoord.z) <= std::abs(In.ClipSpaceCoord.w);}
                                           );
    constexpr float EPSILON = 1e-6;
    auto Inside = [](const Vec4f& line, const Vec4f& p) -> bool
    {
        float d = line.x * p.x + line.y * p.y + line.z * p.z + line.w * p.w;
        return d > -EPSILON;
    };
    auto Intersect = [](const VertexOut& v1, const VertexOut& v2, const Vec4f& line) -> VertexOut
    {
        float da = v1.ClipSpaceCoord.x * line.x + v1.ClipSpaceCoord.y * line.y + v1.ClipSpaceCoord.z *line.z + v1.ClipSpaceCoord.w * line.w;
        float db = v2.ClipSpaceCoord.x * line.x + v2.ClipSpaceCoord.y * line.y + v2.ClipSpaceCoord.z *line.z + v2.ClipSpaceCoord.w * line.w;
        float weight = da / (da - db);
        return v1 + (v2 - v1) * weight;
    };
    const std::vector<Vec4f> ViewPlanes = {
        //Near
        Vec4f(0,0,1,1),
        //far
        Vec4f(0,0,-1,1),
        //left
        Vec4f(1,0,0,1),
        //top
        Vec4f(0,1,0,1),
        //right
        Vec4f(-1,0,0,1),
        //bottom
        Vec4f(0,-1,0,1)
    };
    if(AllVertexInsideOfCVV) return InVertex;
    std::vector<VertexOut> OutVertex{InVertex[0], InVertex[1], InVertex[2]};
    for(const auto& ViewPlane : ViewPlanes)
    {
        std::vector<VertexOut> input(OutVertex);
        OutVertex.clear();
        for(int j = 0; j < input.size(); j++)
        {
            VertexOut current = input[j];
            VertexOut last = input[(j + input.size() - 1) % input.size()];
            if (Inside(ViewPlane, current.ClipSpaceCoord))
            {
                if(!Inside(ViewPlane, last.ClipSpaceCoord))
                {
                    VertexOut intersecting = Intersect(last, current, ViewPlane);
                    OutVertex.push_back(intersecting);
                }
                OutVertex.push_back(current);
            }
            else if(Inside(ViewPlane, last.ClipSpaceCoord))
            {
                VertexOut intersecting = Intersect(last, current, ViewPlane);
                OutVertex.push_back(intersecting);
            }
        }
    }

    return OutVertex;
}

Tangent Space Normal Mapping

存储在模型顶点的**切线空间(tangent space)**中，优势：

  1. 切线空间存储的是相对法线信息，因此换个网格（或者网格变换deforming）应用该纹理，也能得到合理的结果。
  2. 可以进行uv动画，通过移动该纹理的uv坐标实现凹凸移动的效果，这种UV动画在水或者火山熔岩这种类型的物体会会用到。
  3. 重用法线纹理节省内存，比如,一个砖块,我们仅使用一张法线纹理就可以用到所有的6个面，无需对每个面有一个发现贴图，这样大大减少了法线贴图的大小。
  4. 可以压缩。因为切线空间的法线z方向总是正方向，因此可以仅存储xy方向，从而推导z方向（存储的法线向量是单位向量，用勾股定理由xy得出z，取z为正的一个即可）。

项目wiki上的理解/公式推导: Summary of TagentSpaceNormal, TBN Matrix, TBN Coordinate

HDR/AECS ToneMapping

A very elegant fitting.

float3 ACESToneMapping(float3 color, float adapted_lum)
{
	const float A = 2.51f;
	const float B = 0.03f;
	const float C = 2.43f;
	const float D = 0.59f;
	const float E = 0.14f;

	color *= adapted_lum;
	return (color * (A * color + B)) / (color * (C * color + D) + E);
}
With ACES ToneMapping Without ACES ToneMapping
image-20231128150403640 image-20231128150312255

Shadow Mapping

The Most Basic Method Of Shadow Mapping

这里我们可视化下Light视角下的DepthBuffer

Depth Buffer（In Light View）
image-20231129161027212
With Shadow Without Shadow
image-20231129173100355 image-20231128150403640

会出现的几个问题：

  • 阴影失真与自遮挡(Shadow Acne)

  • 阴影悬浮(Shadow Peter-panning)

  • 阴影锯齿(Shadow Aliasing)

  • 大场景中Shadow Map找不到对应的点(CSM)

Shadow Acne和自遮挡

image-20231224202229441

上图出现了条状的阴影:

image-20231224202314452

以方向光源为例，一般认为方向光是平行光，在光源处渲染时使用正交投影。因为Shadow Map的分辨率有限，Shadow Map上面的**一个片段**对应场景中的**一块区域**，又因为很多情况下光源与物体存在夹角，因此记录的深度通常与物体的实际深度存在偏差。

​ 上图中蓝色片段即为ShadowMap中记录的深度。在纹理中像素为最小单位，一个像素只能记录一个值，图中每个像素记录的是箭头处的深度。这就导致了明明本该整块被照亮的地板，会出现明暗相间的条纹：黑线处的地板由于在光源视角中深度小于记录的值，因此不在阴影中。红线处的地板深度大于记录的值，没有通过阴影测试。

​ 解决办法有些许trick，我们可以用一个叫做阴影偏移（shadow bias）的技巧来解决这个问题，我们简单的对表面的深度（或深度贴图）应用一个偏移量，这样片元就不会被错误地认为在表面之下了。

image-20231224202630631

float shadowFactor = 1.0f;
if((int)CorrespondingPoint.x < DepthBuffer.size() && (int)CorrespondingPoint.y < DepthBuffer[(int)CorrespondingPoint.x].size())
{
    shadowFactor = 0.3f + 0.7f*(DepthBuffer[(int)CorrespondingPoint.x][(int)CorrespondingPoint.y] > CorrespondingPoint.z - 1);//1 is shadow bias
}

我们这里简单的用了1作为bias， 阴影基本正常：

image-20231224202923283

因为阴影失真的问题是由于光线和物体表面的夹角导致的，光线越垂直于物体，失真的影响就越小，因此通常会将bias与光线和物体表面法线的夹角挂钩：

$\text { bias }=k \cdot(1.0-\operatorname{dot}(\text { normal, lightDir }))$

//Shadow
Vec3f p(0, 0, 0);
for (int i=0;i<3;i++)//坐标插值
{
	p = p + Varying_tri[i] * bar.raw[i];
}
Matrix<4, 1, float>CorrespondingPointInShadowBuffer = Uniform_MShadow * Matrix<4, 1, float>::Embed(p);
CorrespondingPointInShadowBuffer /= CorrespondingPointInShadowBuffer.raw[3][0];
Vec3f CorrespondingPoint{ CorrespondingPointInShadowBuffer.raw[0][0], CorrespondingPointInShadowBuffer.raw[1][0], CorrespondingPointInShadowBuffer.raw[2][0] };

float shadowFactor = 1.0f;
constexpr float shadowK = 1.0f;
float shadowBias = shadowK*(1.0f - n*l);

if ((int)CorrespondingPoint.x < DepthBuffer.size() && (int)CorrespondingPoint.y < DepthBuffer[(int)CorrespondingPoint.x].size())
{
	shadowFactor = 0.3f + 0.7f*(DepthBuffer[(int)CorrespondingPoint.x][(int)CorrespondingPoint.y] > CorrespondingPoint.z - shadowBias);//1 is shadow bias
}
阴影悬浮(Shadow Peter-panning)和Shadow Bias

这其实是由于ShdowBias导致的：

image-20231224204404293

本来不能通过阴影测试，bias设置过大，导致本该被遮挡的物体，因为减去了bias导致深度值变小，通过了阴影测试。

解决方法：

1.其实bias设置合理一点即可，不要太大。

2.也可以当渲染深度贴图时候使用正面剔除（front face culling），我们只利用背面，这样阴影失真也解决了，不再需要bias的辅助。使用这个方法可以免去反复调整bias，并且也不会导致悬浮的问题。但使用该方法的前提是场景中的物体必须是一个体（有正面和反面）而非原先的一个面。

阴影走样Shadow Aliasing

我们上述的阴影有的锯齿：

image-20231224211837915

  • 锯齿本质是采样频率不够，最直接的解决方法就是 提高采样频率，但也会带来时间/空间的开销
  • 使用PCF/PCSS等各种效果更好的阴影算法

PCF(Percentage Closer Filtering)

​ PCF全称是Percentage Closer Filtering，优化阴影测试时的采样方式，对一个ShadowMap上的点的周围3*3采样，相当于模糊处理，以节约阴影锯齿的问题。

image-20240311133030956

注意这里不是对shadowMap做模糊，而是如果有一点是ShadowMap对其周围泊松分布采样算出其被遮挡的比例作为阴影系数。

image-20240311133328519

Without PCF With PCF
image-20231226201932225 image-20231226202027397

PCSS(Percentage-Closer Soft Shadows)

PCF虽然“软化”了阴影，但是我们阴影往往是由硬阴影+软阴影组成，PCF这种全软化的方式算不上很好的效果。

现实中的阴影往往是如下图，沿着红线越来越“软”

image-20231228171039621

PCSS就是动态适应的选择PCF模糊的size：

image-20231228171344785

如上图，只需要遮挡处到光源处的竖直距离$d_{Blocker}$, 投射阴影处到光源处的竖直距离$d_{Receiver}$，还需要一个光源大小$W_{Light}$,

image-20240102214451107

​ 可以发现法线过度生硬，这是因为$d_{Blocker}$出现了突变，即我们计算average $d_{Blocker}$的时候选择的采样半径太小，导致变化不够平滑，我们调整计算平均$d_{Blocker}$的采样大小为40，$W_ {light}$大小为50，此时过度平滑了很多

image-20240102215517557

​ 我们使用上述的两种软阴影方法PCF/PCSS中，不难发现因为做高斯模糊导致在脚趾处有一定的漏光，这是因为对于脚趾边缘的阴影点在计算时高斯模糊导致了边缘很软，解决漏光的方法也很直接，使用带权的高斯模糊，而不是权重相同，权重可以以两个点之间的世界空间距离的倒数作为权重，即两个点差距很大(一点在地板的阴影上，另一个点在脚趾上)，这个点的权重贡献会很小。

AO(Ambient Occlusion)

SSAO(Screen-Space Ambient Occlusion)

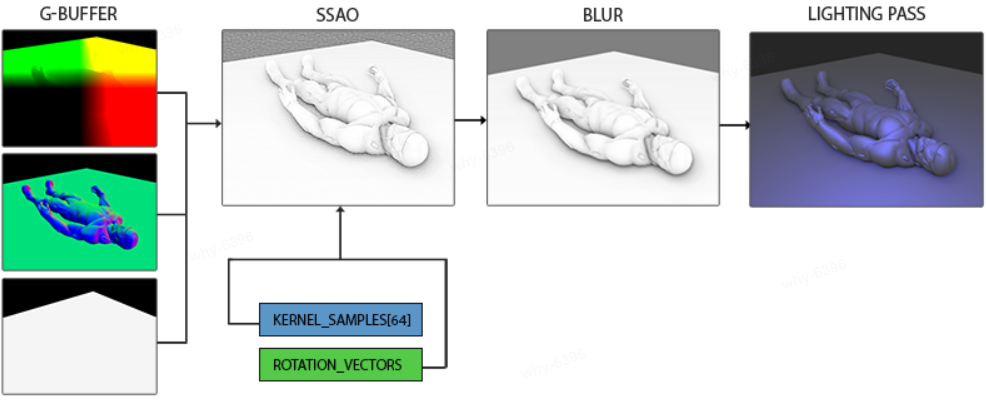
实现的几个细节：

  • 物体相差远的地方, 会在深度图上误认为有AO,实际上不应该有AO，所以要做RangeCheck

    image-20231205011832980

  • 降噪: 双边滤波

  • 降采样提升运行效率

  • 法向半球采样 + 加速插值函数(将核心样本靠近原点分布)

工作流：

image-20240115142822822

最后效果:

image-20240117205040340

HBAO(Image-space Horizon-based Ambient Occlusion)

HBAO

With HBAO Without HBAO
image-20231204200320537 image-20231204201046444

工作流是:

  • 降低分辨率
  • 对每个随机方向进行RayMarching找最大水平角
  • 做Blur

HBAO(屏幕空间的环境光遮蔽) - YiQiuuu的文章 - 知乎 https://zhuanlan.zhihu.com/p/103683536

PBR

Metallic-Roughness Workflow:

四个点光源下渲染结果：

image-20240229150810871

image-20240305155133325

IBL

Diffuse IBL

Without Diffuse IBL With Diffuse IBL
image-20240307161331107 image-20240307161008694

渲染方程为：

$$ L_o(p,\omega_o)=\int\limits_\Omega(k_d\frac{c}{\pi})L_i(p,\omega_i)n\cdot\omega_id\omega_i+\int\limits_\Omega(k_s\frac{DFG}{4(\omega_o\cdot n)(\omega_i\cdot n)})L_i(p,\omega_i)n\cdot\omega_id\omega_i $$

我们只考虑第一项漫反射项：

$$ \int\limits_\Omega(k_d\frac{c}{\pi})L_i(p,\omega_i)n\cdot\omega_id\omega_i $$

这项可以预处理，其中我们认为p总在中心点，然后对每个法向$n$进行radiance采样合成irradiance即可，进行预计算即可。

采样时获取对应预计算贴图处的信息即可，预计算贴图为：

Specular IBL

Without Specular IBL With Speular IBL
image-20240309222433670 image-20240309222335355

渲染方程在镜面项式子如下：

$$ L_o(p,\omega_o)=\int\limits_\Omega(k_s\frac{DFG}{4(\omega_o\cdot n)(\omega_i\cdot n)}L_i(p,\omega_i)n\cdot\omega_id\omega_i=\int\limits_\Omega f_r(p,\omega_i,\omega_o)L_i(p,\omega_i)n\cdot\omega_id\omega_i $$

做Split Sum得到：

$$ L_o(p,\omega_o)\approx \int\limits_\Omega L_i(p,\omega_i)d\omega_i*\int\limits_\Omega f_r(p,\omega_i,\omega_o)n\cdot\omega_id\omega_i $$

首先考虑第一部分：

$$ \int\limits_{\Omega}L_{i}(p,\omega_{i})d\omega_{i} $$

这部分和漫反射部分有些区别是，考虑N项决定了高光的波瓣lobe，这部分需要对不同粗糙度进行区别。

image-20240715150258220

我们这里为了更快的收敛速度使用重要性采样，也就是我们设计一个新的pdf来指导采样，推导如下：

我们设发现分布函数为$D(\theta)$:

$$ \mathrm{D}(\theta)=\frac{\alpha^2}{\pi\left(\cos^2(\theta)(\alpha^2-1)+1\right)^2} $$

在设计新的概率分布函数时，我们所期待的是：让$D(\theta)$更大的，即更接近lobe的贡献更大，因此我们设计PDF是要向$D(\theta)$靠拢, 我们这样设计PDF：

$$ \mathrm{p}(\theta,\phi)=\mathrm{D}(\theta)\cos(\theta)\sin(\theta)\quad $$

这个PDF的另一个好处就是其还是normalized的，证明如下：

$$ \int\limits_{\phi=0}^{2\pi}\int\limits_{\theta=0}^{\frac{\pi}{2}}\mathrm{D}(\theta)\cos(\theta):\sin(\theta):d\theta:d\phi=1$$ $$\int\limits_{\phi=0}^{2\pi}\int\limits_{\theta=0}^{\frac{\pi}{2}}\frac{\alpha^2\cos(\theta)\sin(\theta)}{\pi\left((\alpha^2-1)\cos^2(\theta)+1\right)^2}d\theta:d\phi=1$$ $$\begin{aligned}2\pi\left[\frac{\alpha^2}{\pi\left(2\alpha^2-2\right)\left(\left(\alpha^2-1\right)\cos^2(\theta)+1\right)}\right]_0^{\frac{\pi}{2}}&=1\1&=1\quad\end{aligned}$$

我们计算CDF：

image-20240715151805494

image-20240715151822803

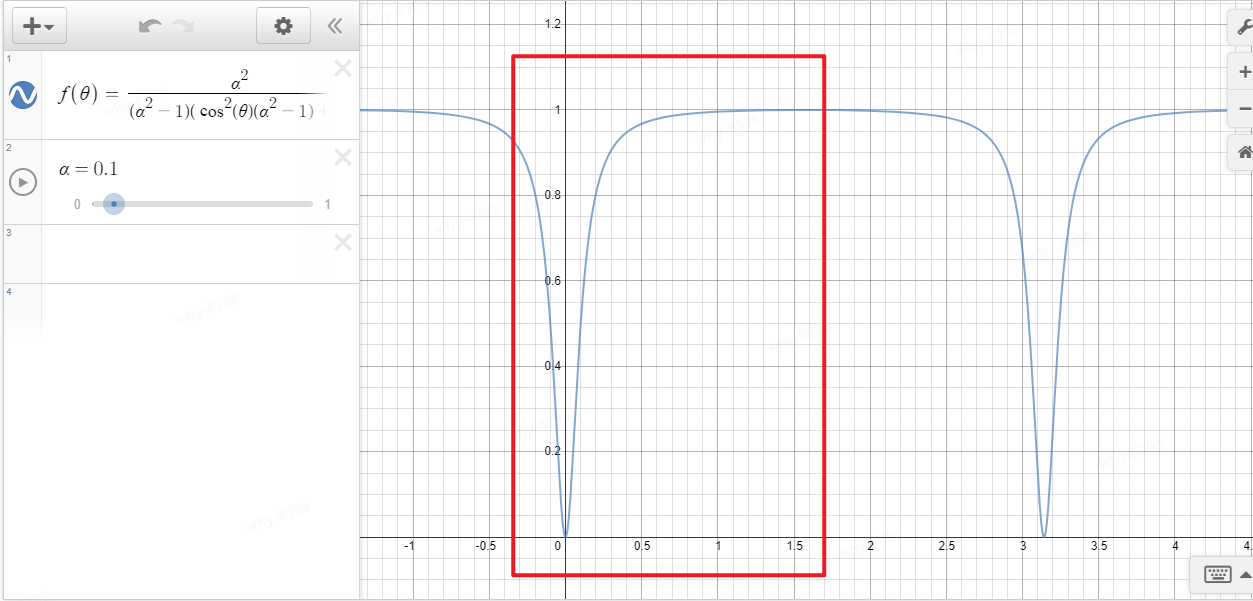
​ 我们看下对于v变量和$\theta$的关系： 当粗糙度很低(0.1)时, 当随机选择v(竖轴)时，总会在$\theta$很小处，即此时采样主要在lobe处。

image-20240715154443729

​ u，v就是我们新的分布，我们可以直接对u，v应用uniform分布，但是为了加速收敛，选择低差异序列，传统蒙特卡洛方法使用伪随机数生成样本点，这些点在高维空间中可能会出现聚集或空隙现象，从而导致估计不稳定。拟蒙特卡洛方法使用确定性的低差异序列（如Sobol序列、Halton序列等）生成样本点，这些点在高维空间中分布更加均匀，减少了空隙和重叠的现象，提高了估计的稳定性。

最后预处理得到不同粗糙度下的预滤波环境贴图：

image-20240715152239702

CubeMap

天空盒的做法十分简单，即渲染六个包围面

image-20240223183212808

Scene Management

Multi Objects Render Pipeline is supported.

Reference

About

A Software Renderer Based on C++20

Resources

Readme
Activity

Stars

2 stars

Watchers

1 watching

Forks

2 forks
Report repository

Releases

No releases published

Packages

No packages published

Languages