Implement SIBC (Leontovich boundary condition) for good conductors

[elenafuengar]

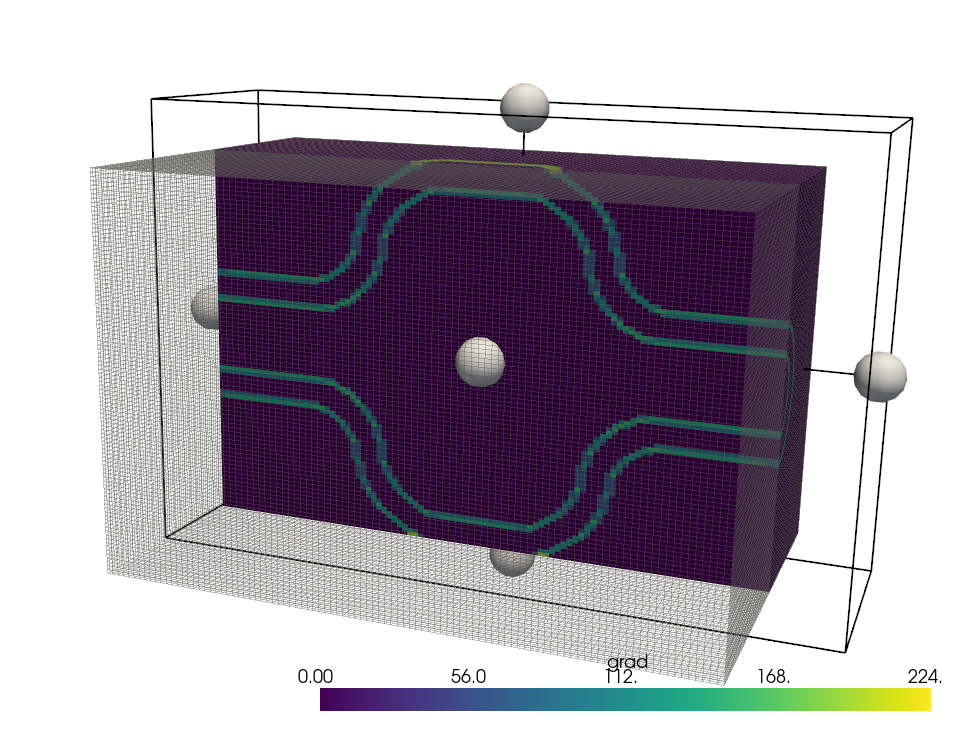
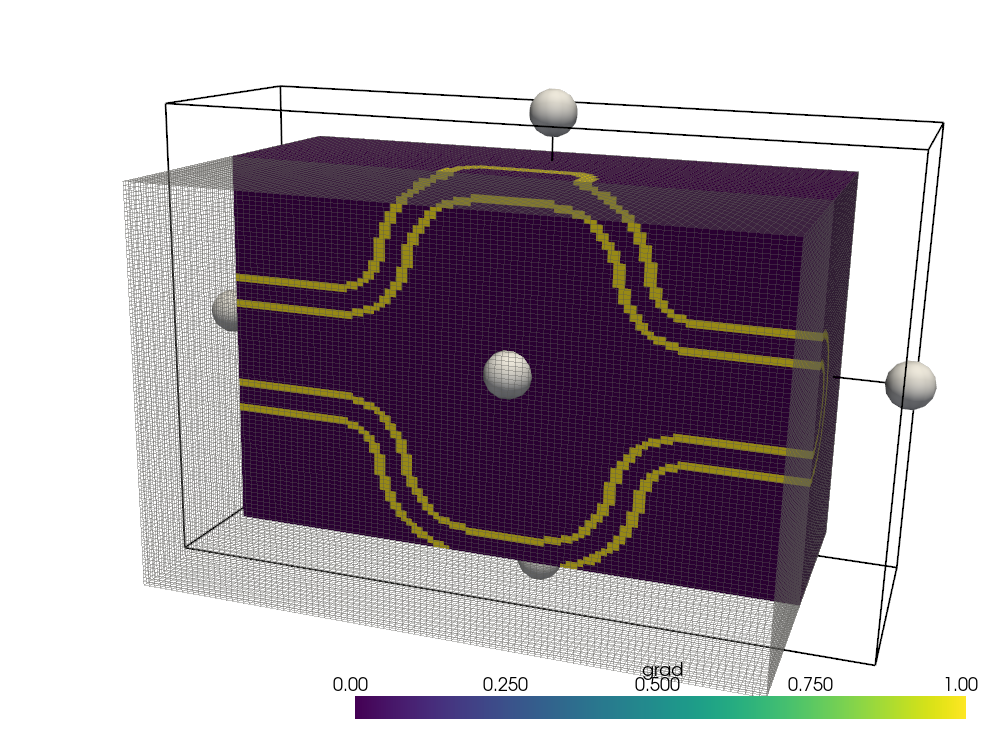
📝 Pull Request Summary

This pull request introduces several improvements and refactorings to the handling of STL-based materials and the solver infrastructure for the 3D grid simulation package. The main changes focus on enhancing flexibility in material assignment, supporting the Surface Impedance Boundary Condition (SIBC) for high-conductivity materials, and refactoring solver methods for better code organization and maintainability.

🔧 Changes Made

STL Material Handling and SIBC Support

• Added support for SIBC (Leontovich boundary condition) in GridFIT3D, which is automatically applied to STL solids with conductivity greater than 1e3 S/m. This involves marking only the surface cells for such materials. (wakis/gridFIT3D.py) [1] [2] [3]
• Improved STL material assignment: string keys are now mapped to material properties using material_lib, and all STL material data is normalized to dictionary format for consistency. (wakis/gridFIT3D.py)
• Changed the default vacuum material representation from 'vacuum' to [1.0, 1.0] for consistency and improved opacity handling in plotting. (tests/test_007_mpi_lossy_cavity.py, wakis/gridFIT3D.py) [1] [2]

Solver Infrastructure Refactoring

• Refactored solver step and MPI-related methods to use private method naming (_one_step, _mpi_one_step, etc.), improving code clarity and encapsulation. Public methods now delegate to these internal implementations. (wakis/solverFIT3D.py) [1] [2] [3] [4] [5] [6]
• Consolidated STL material application logic into a new _apply_stl_materials method in the solver, ensuring correct assignment of permittivity, permeability, and conductivity to grid cells. (wakis/solverFIT3D.py) [1] [2]

Other Improvements

• Updated legacy conductor support methods with private naming and deprecation notices, preparing for future removal. (wakis/solverFIT3D.py) [1] [2] [3]
• Updated the test simulation to use the refactored one_step method instead of the old MPI-specific method for improved compatibility. (tests/test_007_mpi_lossy_cavity.py)

✅ Checklist

• Code follows the project's style and guidelines
• Added tests for new functionality
• Updated documentation (mentioned in docs/ or included in examples/ and notebooks/)
• Verified that changes do not break existing functionality (automatic tests passing)

📌 Related Issues / PRs

Closes #45

[elenafuengar]

🔍 Algorithm explanation

This snippet tags the surface of solid regions by computing the gradient magnitude of a scalar field (e.g. material mask) and converting it to a boolean mask. It uses PyVista's Gradient filter:

    def _mark_cells_in_surface(self):
        # Modify the STL mask to account only for the surface
        for key in self.stl_solids.keys():
            if len(self.stl_materials[key]) == 3 and self.stl_materials[key][2] > 1e3:
                grad = np.array(self.grid.compute_derivative(scalars=key)['gradient']) #bool STL mask
                grad = np.sqrt(grad[:, 0]**2 + grad[:, 1]**2 + grad[:, 2]**2) #from 0 to 255
                self.grid[key] = grad.astype(bool)

The surface is identified where the gradient of the scalar field is non-zero:

$|\nabla \phi| = \sqrt{ (\partial_x \phi)^2 + (\partial_y \phi)^2 + (\partial_z \phi)^2 }$

Cells where $|\nabla \phi| > 0$ are marked as surface.

SIBC	SIBC bool	No SIBC

[elenafuengar]

Maximum Conductivity Resolvable Without a Leontovich Boundary

To accurately model a conducting material volumetrically in FIT/FDTD, the skin depth

$$\delta = \sqrt{\frac{2}{2\pi f_{\max},\mu_0,\sigma}}$$

must be resolved by the grid. A common requirement is at least 3 cells per skin depth, i.e.

$$\delta \gtrsim 3\Delta_n$$

where $(\Delta_n)$ is the grid spacing normal to the wall, considered as $\sqrt{2}\cdot \text{min}(\Delta x, \Delta y, \Delta z)$. Substituting the skin-depth expression and solving for $(\sigma)$ gives the maximum conductivity that can be volumetrically resolved at a target frequency $(f_{\max})$:

$$\sigma_{\max} = \frac{1}{9\pi f_{\max},\mu_0\Delta_n^2}$$

Materials with $(\sigma > \sigma_{\max})$ have a skin depth too small to be captured by the mesh and should be modeled using a Leontovich (surface impedance) boundary condition instead of volumetric conductivity.

[elenafuengar]

Surface Parameters for the Leontovich (SIBC) Boundary

For a good conductor, the Leontovich surface impedance has the form

$$Z_s = (1+j)\sqrt{\dfrac{\omega\mu}{2\sigma}}$$

meaning that the resistive and reactive parts are equal (a $45^\circ$ phase).
In the SIBC implementation, we approximate $Z_s$ by its magnitude-based form

$$Z_s \approx \sqrt{\pi f_{\max}\mu / \sigma}$$

and define an equivalent surface admittance

$$Y_s = 1/Z_s$$

To embed this into the time-domain FIT update, we convert $Y_s$ into effective
surface parameters:

• surface conductivity: $\sigma_s = 1/Z_s$
• surface permittivity term: $\varepsilon_s = 1/Z_s$

Both appear with the same magnitude because the $45^\circ$ impedance angle implies
equal real and imaginary parts in the admittance. These values are applied only to
boundary edges or cells marked as SIBC, replacing the volumetric response of the metal.