You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
@@ -197,7 +197,9 @@ The **DC power flow model** provides a linearized approximation of AC power flow
197
197
198
198
# ╔═╡ 7b4800c2-133d-4793-95b1-a654a4f19558
199
199
md"""
200
-
### DC Optimal Power Flow Formulation
200
+
### DC Power Flow Formulation
201
+
202
+
The DC power flow optimization problem combines economic dispatch with network physics:
201
203
202
204
```math
203
205
\begin{align}
@@ -209,20 +211,20 @@ md"""
209
211
\end{align}
210
212
```
211
213
212
-
- Reactance of line: $x_{ij}$. $\frac{1}{x_{ij}} = b_{ij}$: susceptance (specified by equipment manufacturer)
213
-
- Reference bus: only for modeling, you can pick any bus as the reference bus. We only care about angle differences (which carries current through lines)
214
+
- Reactance of line $x_{ij}$. $\frac{1}{x_{ij}} = b_{ij}$: susceptance (manufacturer specified)
215
+
- Reference bus: only for modeling, you can pick any bus as the reference bus. We only care about angle differences (which carries current through lines
Let's apply the DC power flow formulation to the 3-bus network with line constraints:
223
+
Let's apply the DC power flow formulation to our 3-bus network with line constraints:
222
224
223
225
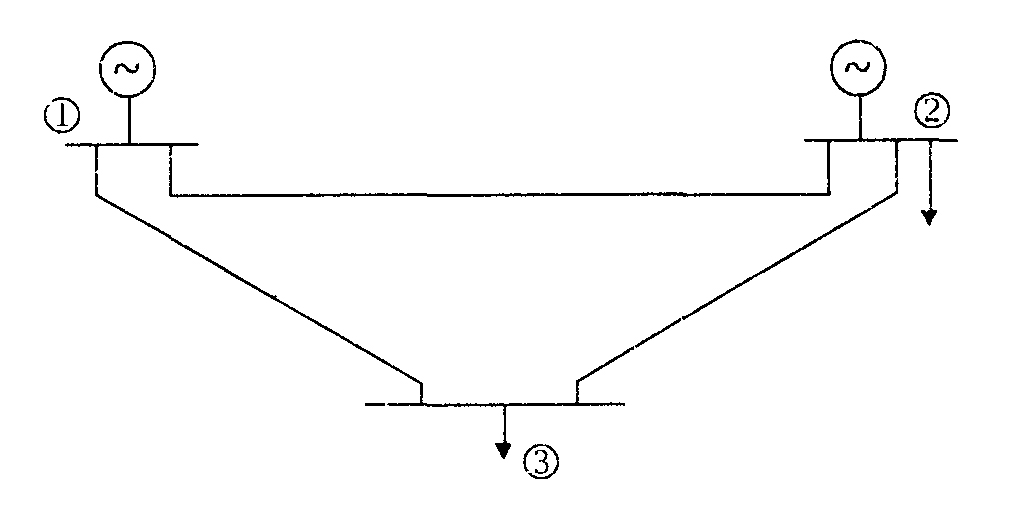
224
226
225
-
**Net generation calculations:**
227
+
**How did I get the numbers:**
226
228
- Assume P1 generates 85 MW, with 50 MW of load, the net injection is 35 MW
227
229
- Assume P2 generates 40 MW, with no load, net injection is 40 MW (we take upwards arrow as injection)
228
230
- Bus 3 has no gen, only load
@@ -232,7 +234,7 @@ Let's apply the DC power flow formulation to the 3-bus network with line constra
232
234
md"""
233
235
### DCOPF Solution
234
236
235
-
Consult lecture slides for the solution and detailed analysis. Observe how adding line limits changes dispatch and total cost.
237
+
Consult lecture slides for the solution and detailed analysis.
236
238
"""
237
239
238
240
# ╔═╡ f72775b9-818c-4a9b-9b66-cfccd88e17ed
@@ -241,10 +243,9 @@ md"""
241
243
242
244
This section has introduced the fundamentals of static optimal power flow problems including economic dispatch and DC optimal power flow. Key takeaways:
243
245
244
-
- You observed that without thermal limits, optimal dispatch from ED can overload lines
245
-
- Real systems are AC (complex voltages/currents) -- much harder. This is just a lightweight intro so we can think about expressing real-world problems as optimization formulations without burdening ourselves with AC physics, which we will see in transient stability section.
246
-
247
-
In the next section, we introduce transients and transient stability constraints to capture dynamic states of grid components, bringing time domain dynamics into the optimization.
246
+
- You will see that without thermal limits, optimal dispatch can overload lines
247
+
- Reference bus is arbitrarily picked by the solver.
248
+
- Real systems are AC (complex voltages/currents) -- much harder. This is just a lightweight intro so we can think about expressing real-world problems as optimization formulations without overburdening ourselves with AC physics, which we will see in transient stability section.
This relates how fast the mass is spinning ($\omega$) to the imbalance of power input (generation) and power withdrawal (load + losses).
949
-
"""
950
-
951
-
# ╔═╡ 3a911e1a-5ec9-4eb0-9ec5-4ee2502e5103
952
-
md"""
953
-
## From Torque to Power (Continued)
954
950
955
951
In practice, generators operate close to system frequency, so the generators spin at an angular velocity that is close to that 60 Hz constant. Since the variations are mostly tiny, we can define inertia constant $M = J\omega$
956
952
@@ -991,7 +987,7 @@ So we have per unit swing:
991
987
992
988
# ╔═╡ abcd31d0-c6eb-4bc7-a752-83a8d7f6fda1
993
989
md"""
994
-
## Damping and Advanced Forms
990
+
## Damping and Another Form of Generator Swing Equations
995
991
996
992
Some also add damping:
997
993
@@ -1080,7 +1076,7 @@ M_{\text{virtual}} \dot{\omega} = P_{\text{ref}} - P
1080
1076
1081
1077
# ╔═╡ 0a2c4c0a-c68e-4f21-afbb-1b80791ec166
1082
1078
md"""
1083
-
## Virtual Inertia (continued)
1079
+
## Virtual Inertia
1084
1080
1085
1081
**How it works:**
1086
1082
- The inverter adjusts its internal frequency reference according to power imbalance
@@ -1172,11 +1168,6 @@ Power-flow balance:
1172
1168
P_G - P_D = \text{network losses}, \qquad
1173
1169
Q_G - Q_D = 0.
1174
1170
```
1175
-
"""
1176
-
1177
-
# ╔═╡ 2644c1ad-c1aa-4b03-ab27-fb414c03e3af
1178
-
md"""
1179
-
## Steady-State Load Models Continued
1180
1171
1181
1172
However, the static load model has important limitations. Interpretation of the above model:
1182
1173
- Loads are fixed regardless of system conditions, or at most respond to nodal voltage.
## Adaptive Exponential Recovery Load (ERL) Model (continued)
1346
1329
1347
1330
- Nominal power withdrawals at reference voltage $V_0$: $P_0, Q_0$
@@ -1413,7 +1396,8 @@ md"""
1413
1396
1414
1397
# ╔═╡ 011a1e50-0316-42ec-9295-eeee64b76299
1415
1398
md"""
1416
-
## Why We Go Beyond Steady-State OPF
1399
+
## Wrap up
1400
+
### Why We Go Beyond Steady-State OPF
1417
1401
1418
1402
In this chapter, we motivated from the physical principles and operation constraints to demonstrate that power systems are fundamentally dynamic. **The bigger picture:**
1419
1403
- Even though steady-state analysis is helpful for many purposes and have lower computational burden, power systems are **dynamic systems.**
@@ -1423,7 +1407,7 @@ In this chapter, we motivated from the physical principles and operation constra
1423
1407
1424
1408
# ╔═╡ 81952b3e-93c9-4179-8b12-5933d49749a6
1425
1409
md"""
1426
-
## Four Building Blocks of System Dynamics
1410
+
### Four Building Blocks of System Dynamics
1427
1411
1428
1412
Throughout this chapter, we have explored four fundamental components that govern power system dynamics:
1429
1413
@@ -1435,7 +1419,7 @@ Throughout this chapter, we have explored four fundamental components that gover
1435
1419
1436
1420
# ╔═╡ a3b4c5d6-0894-4340-a18b-72f8e1204503
1437
1421
md"""
1438
-
## Why We Need Dynamic Optimization (TSC-OPF)
1422
+
### Why We Need Dynamic Optimization (TSC-OPF)
1439
1423
1440
1424
These building blocks come together in transient stability-constrained optimization. **Why we need optimization with system dynamics embedded (TSC-OPF):**
1441
1425
- Steady-state OPF finds an economical operating point **only at equilibrium.**
@@ -1446,80 +1430,76 @@ These building blocks come together in transient stability-constrained optimizat
0 commit comments