You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
33
+
34
+
Now let's start digging into MTK!
35
+
9
36
## Your very first ODE
10
37
11
38
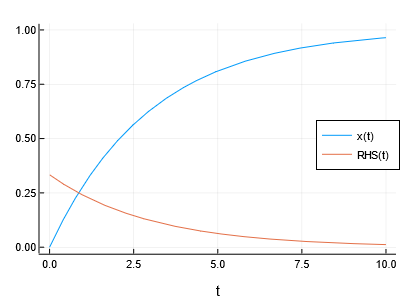
Let us start with a minimal example. The system to be modelled is a
@@ -16,9 +43,10 @@ first-order lag element:
16
43
\dot{x} = \frac{f(t) - x(t)}{\tau}
17
44
```
18
45
19
-
Here, ``t`` is the independent variable (time), ``x(t)`` is the (scalar) state variable,
20
-
``f(t)`` is an external forcing function, and ``\tau`` is a constant parameter. In MTK, this system can be modelled as follows. For simplicity, we first set the forcing function to
21
-
a constant value.
46
+
Here, ``t`` is the independent variable (time), ``x(t)`` is the (scalar) state
47
+
variable, ``f(t)`` is an external forcing function, and ``\tau`` is a constant
48
+
parameter. In MTK, this system can be modelled as follows. For simplicity, we
49
+
first set the forcing function to a constant value.
22
50
23
51
```julia
24
52
using ModelingToolkit
@@ -57,6 +85,7 @@ from the actual symbolic elements to their values, represented as an array
57
85
of `Pair`s, which are constructed using the `=>` operator.
58
86
59
87
## Algebraic relations and structural simplification
88
+
60
89
You could separate the calculation of the right-hand side, by introducing an
61
90
intermediate variable `RHS`:
62
91
@@ -72,10 +101,11 @@ intermediate variable `RHS`:
72
101
# τ
73
102
```
74
103
75
-
To directly solve this system, you would have to create a Differential-Algebraic Equation (DAE)
76
-
problem, since besides the differential equation, there is an additional algebraic equation now.
77
-
However, this DAE system can obviously be transformed into the single ODE we used in the
78
-
first example above. MTK achieves this by means of structural simplification:
104
+
To directly solve this system, you would have to create a Differential-Algebraic
105
+
Equation (DAE) problem, since besides the differential equation, there is an
106
+
additional algebraic equation now. However, this DAE system can obviously be
107
+
transformed into the single ODE we used in the first example above. MTK achieves
@@ -111,6 +143,7 @@ values of `x` matching `sol.t`, etc. Note that this works even for variables
111
143
which have been eliminated, and thus `sol[RHS]` retrieves the values of `RHS`.
112
144
113
145
## Specifying a time-variable forcing function
146
+
114
147
What if the forcing function (the "external input") ``f(t)`` is not constant?
115
148
Obviously, one could use an explicit, symbolic function of time:
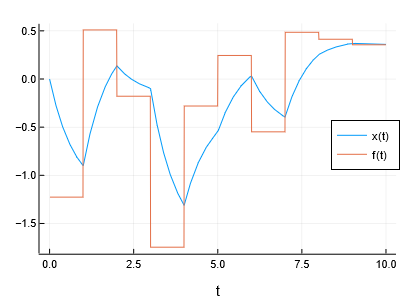
116
149
@@ -120,9 +153,11 @@ Obviously, one could use an explicit, symbolic function of time:
120
153
```
121
154
122
155
But often there is time-series data, such as measurement data from an experiment,
123
-
we want to embedd as data in the simulation of a PDE, or as a forcing function on the right-hand side of an ODE -- is it is the case here. For this, MTK allows to "register" arbitrary
124
-
Julia functions, which are excluded from symbolic transformations but are just used
125
-
as-is. So, you could, for example, interpolate a given time series using
156
+
we want to embed as data in the simulation of a PDE, or as a forcing function on
157
+
the right-hand side of an ODE -- is it is the case here. For this, MTK allows to
158
+
"register" arbitrary Julia functions, which are excluded from symbolic
159
+
transformations but are just used as-is. So, you could, for example, interpolate
we illustrate this option by a simple lookup ("zero-order hold") of a vector
128
163
of random values:
@@ -141,13 +176,11 @@ plot(sol, vars=[x,f])
141
176
142
177
143
178
144
-
145
179
## Building component-based, hierarchical models
146
180
147
-
Working with simple one-equation systems is already fun, but composing more complex systems from
148
-
simple ones is even more fun. Best practice for such a "modeling framework" could be to use
149
-
150
-
factory functions for model components:
181
+
Working with simple one-equation systems is already fun, but composing more
182
+
complex systems from simple ones is even more fun. Best practice for such a
183
+
"modeling framework" could be to use factory functions for model components:
151
184
152
185
```julia
153
186
functionfol_factory(separate=false;name)
@@ -162,17 +195,17 @@ function fol_factory(separate=false;name)
162
195
end
163
196
```
164
197
165
-
Such a factory can then used to instantiate the same component multiple times, but allows
166
-
for customization:
198
+
Such a factory can then used to instantiate the same component multiple times,
199
+
but allows for customization:
167
200
168
201
```julia
169
202
@named fol_1 =fol_factory()
170
203
@named fol_2 =fol_factory(true) # has observable RHS
171
204
```
172
205
173
-
Now, these two components can be used as subsystems of a parent system, i.e. one level
174
-
higher in the model hierarchy. The connections between the components again are just
175
-
algebraic relations:
206
+
Now, these two components can be used as subsystems of a parent system, i.e.
207
+
one level higher in the model hierarchy. The connections between the components
The speedup is significant. For this small dense model (3 of 4 entries are populated), using sparse matrices is counterproductive in terms of required memory allocations. For large,
327
+
The speedup is significant. For this small dense model (3 of 4 entries are
328
+
populated), using sparse matrices is counterproductive in terms of required
329
+
memory allocations. For large,
294
330
295
331
hierarchically built models, which tend to be sparse, speedup and the reduction of
296
332
memory allocation can be expected to be substantial. In addition, these problem
297
333
builders allow for automatic parallelism using the structural information. For
298
334
more information, see the [ODESystem](@ref ODESystem) page.
299
335
300
336
## Notes and pointers how to go on
337
+
301
338
Here are some notes that may be helpful during your initial steps with MTK:
302
339
303
340
* Sometimes, the symbolic engine within MTK is not able to correctly identify the
304
-
independent variable (e.g. time) out of all variables. In such a case, you usually
305
-
get an error that some variable(s) is "missing from variable map". In most cases,
306
-
it is then sufficient to specify the independent variable as second argument to
307
-
`ODESystem`, e.g. `ODESystem(eqs, t)`.
308
-
309
-
* A completely macro-free usage of MTK is possible and is discussed in a separate tutorial. This is for package
310
-
developers, since the macros are only essential for automatic symbolic naming for modelers.
311
-
312
-
313
-
* Vector-valued parameters and variables are possible. A cleaner, more consistent treatment of
314
-
these is work in progress, though. Once finished, this introductory tutorial will also
315
-
cover this feature.
341
+
independent variable (e.g. time) out of all variables. In such a case, you
342
+
usually get an error that some variable(s) is "missing from variable map". In
343
+
most cases, it is then sufficient to specify the independent variable as second
344
+
argument to `ODESystem`, e.g. `ODESystem(eqs, t)`.
345
+
* A completely macro-free usage of MTK is possible and is discussed in a
346
+
separate tutorial. This is for package developers, since the macros are only
347
+
essential for automatic symbolic naming for modelers.
348
+
* Vector-valued parameters and variables are possible. A cleaner, more
349
+
consistent treatment of these is work in progress, though. Once finished,
350
+
this introductory tutorial will also cover this feature.
316
351
317
352
Where to go next?
318
353
319
-
* Not sure how MTK relates to similar tools and packages? Read [Comparison of ModelingToolkit vs Equation-Based Modeling Languages](@ref).
320
-
321
-
* Depending on what you want to do with MTK, have a look at some of the other **Symbolic Modeling Tutorials**.
322
-
323
-
* If you want to automatically convert an existing function to a symbolic representation, you might go through the **ModelingToolkitize Tutorials**.
324
-
325
-
* To learn more about the inner workings of MTK, consider the sections under **Basics** and **System Types**.
326
-
```suggestion
327
-
* To learn more about the details of using MTK, consider the sections under **Basics** and **System Types**.
354
+
* Not sure how MTK relates to similar tools and packages? Read
355
+
[Comparison of ModelingToolkit vs Equation-Based Modeling Languages](@ref).
356
+
* Depending on what you want to do with MTK, have a look at some of the other
357
+
**Symbolic Modeling Tutorials**.
358
+
* If you want to automatically convert an existing function to a symbolic
359
+
representation, you might go through the **ModelingToolkitize Tutorials**.
360
+
* To learn more about the inner workings of MTK, consider the sections under
0 commit comments