Diploma_Scheduling_Theory

Navigation:

1. Problem

2. Libraries

3. What programm do?

4. Programm

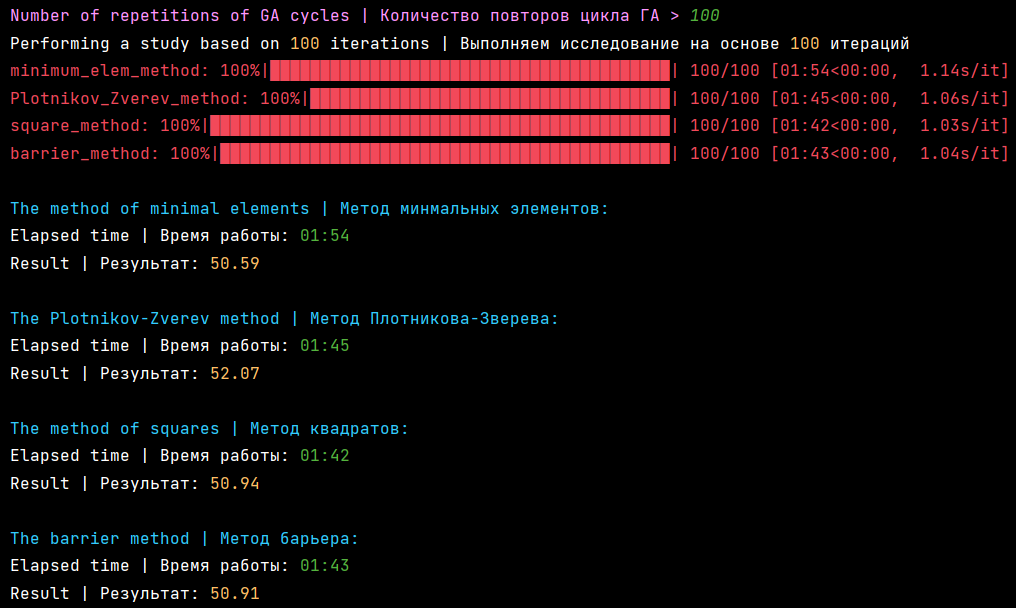
5. Results

1. Problem

The problem of scheduling theory is to efficiently allocate resources over time to achieve specific goals. This problem is important in a wide range of fields, including manufacturing, transportation, healthcare, and computer science. By developing effective scheduling algorithms, businesses and organizations can optimize their operations, reduce costs, and improve productivity.

2. Libraries

3. What programm do?

The program facilitates the creation of an initial population through various partitioning techniques, which will be further elucidated. Moreover, it enables the generation of initial genes based on specific boundaries between two processors.

Methods for the formation of the initial generation

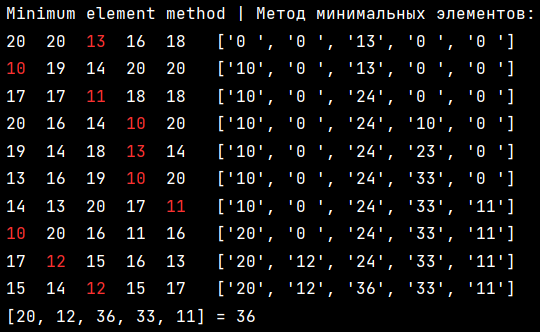
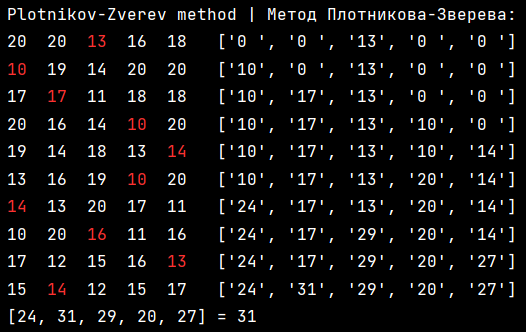
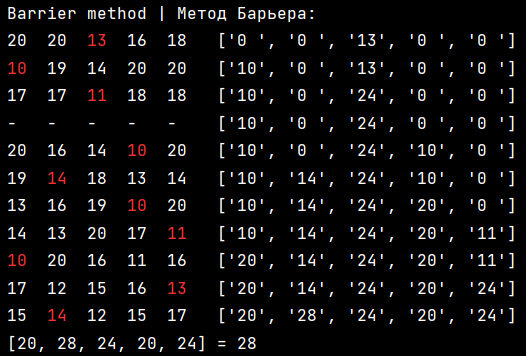
All screens are from methods_analysis.py

The method of minimal elements

The essence of this method is that we simply take the smallest element from each line.

The Plotnikov-Zverev method

A one-dimensional array is formed equal to the number of elements in each row of the matrix. We move this one-dimensional array from the first row of the matrix. For each iteration, we add index-wise the elements of the matrix row and one-dimensional array, then compare and add the element that gives us the smallest difference between the elements of the one-dimensional array.

The barrier method(hybrid of 1 and 2 methods)

The barrier is calculated equal to the sum of loads per processor using the method of minimum elements divided by the number of processors. Before the barrier (-), we calculate by the method of minimal elements, and after by the Plotnikov-Zverev method.

4. Programm

5. The results

Screen is from experiments.py

Screens are from app.py